20.15 - Solved Examples on Matrix Method

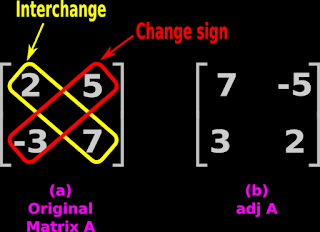
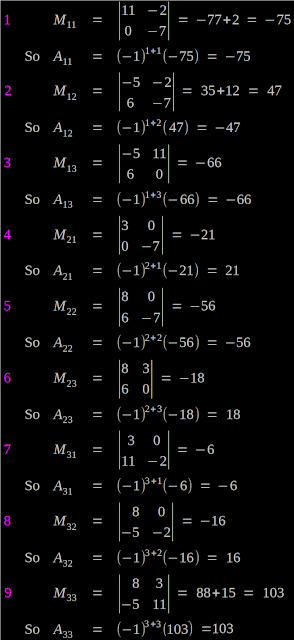In the previous section, we saw the matrix method for solving systems of linear equations. We saw a solved example also. In this section, we will see a few more solved examples.

Solved example 20.24
Solve the system of equations:
2x + 5y = 1
3x + 2y = 7
Solution:
1. The given system can be written in the form AX = B.
$A = \left[\begin{array}{r}                           
2        &{    5    }    \\
3        &{    2    }    \\
\end{array}\right],~X = \left[\begin{array}{r}       
x        \\
y        \\
\end{array}\right]~~ \text{and}~~B = \left[\begin{array}{r}                           
1        \\
7        \\
\end{array}\right]
$

2. So X = A⁻¹ B.
• Check whether A⁻¹ exists:
   ♦ |A| = (4 − 15) = −11
   ♦ |A| ≠ 0
   ♦ So A is a non-singular matrix. Therefore, A⁻¹ exists.

3. Use the method in Solved example 20.21 to find A⁻¹.
We get: $A^{-1} = \left[\begin{array}{r}                           
-2/11        &{    5/11    }    \\
3/11        &{    -2/11    }    \\
\end{array}\right]$

4. Use matrix multiplication to find A⁻¹B.
• We get: X = A⁻¹ B =
$\left[\begin{array}{r}                           
-2/11        &{    5/11    }    \\
3/11        &{    -2/11    }    \\
\end{array}\right]~\left[\begin{array}{r}                           
1        \\
7        \\
\end{array}\right]~ = \left[\begin{array}{r}                        3        \\
-1        \\
\end{array}\right]
$

5. So the solution is: x = 3 and y = -1

Solved example 20.25
Solve the system of equations:
3x − 2y + 3z = 8
2x + y − z = 1
4x − 3y + 2z = 4
Solution:
1. The given system can be written in the form AX = B.
$A = \left[\begin{array}{r}                           
3        &{    -2    } &{    3    }    \\
2        &{    1    } &{    -1    }    \\
4        &{    -3    } &{   2    }    \\
\end{array}\right],~X = \left[\begin{array}{r}       
x        \\
y        \\
z        \\
\end{array}\right]~~ \text{and}~~B = \left[\begin{array}{r}                           
8        \\
1        \\
4        \\
\end{array}\right]
$

2. So X = A⁻¹ B.
• Check whether A⁻¹ exists:
   ♦ |A| = −17 (by expansion along any row or column)
   ♦ |A| ≠ 0
   ♦ So A is a non-singular matrix. Therefore, A⁻¹ exists.

3. Use the method in Solved example 20.20 to find A⁻¹.
We get: $A^{-1} = - \frac{1}{17} \left[\begin{array}{r}                           
-1        &{    -5    } &{    -1    }    \\
-8        &{    -6    } &{    9    }    \\
-10        &{    1    } &{   7    }    \\
\end{array}\right]$

4. Use matrix multiplication to find A⁻¹B.
• We get: X = A⁻¹ B =
$- \frac{1}{17} \left[\begin{array}{r}                           
-1        &{    -5    } &{    -1    }    \\
-8        &{    -6    } &{    9    }    \\
-10        &{    1    } &{   7    }    \\
\end{array}\right]~\left[\begin{array}{r}                           
8        \\
1        \\
4        \\
\end{array}\right]~ = \left[\begin{array}{r}                        1        \\
2        \\
3        \\
\end{array}\right]
$

5. So the solution is: x = 1, y = 2 and z = 3

Solved example 20.26
Sum of three numbers is 6. If we multiply third number by 3 and add second number to it, we get 11. By adding first and third numbers, we get double of second number. Represent it algebraically and find the numbers by matrix method.
Solution:
1. Let the numbers be x, y and z.
2. Given: Sum is 6.
• So we can write: x + y + z = 6
3. Given: If we multiply third number by 3 and add second number to it, we get 11.
• So we can write: 3z + y = 11.
• This is same as 0x + y + 3z = 11
4. Given: By adding first and third numbers, we get double of second number.
• So we can write: x + z = 2y
• This is same as: x − 2y + z = 0
5. From (2), (3) and (4), we get three equations:
x + y + z = 6
0x + y + 3z = 11
x − 2y + z = 0
6. The given system can be written in the form AX = B.
$A = \left[\begin{array}{r}                           
1        &{    1    } &{    1    }    \\
0        &{    1    } &{    3    }    \\
1        &{    -2    } &{   1    }    \\
\end{array}\right],~X = \left[\begin{array}{r}       
x        \\
y        \\
z        \\
\end{array}\right]~~ \text{and}~~B = \left[\begin{array}{r}                           
6        \\
11        \\
0        \\
\end{array}\right]
$

7. So X = A⁻¹ B.
• Check whether A⁻¹ exists:
   ♦ |A| = 9 (by expansion along any row or column)
   ♦ |A| ≠ 0
   ♦ So A is a non-singular matrix. Therefore, A⁻¹ exists.

8. Use the method in Solved example 20.20 to find A⁻¹.
We get: $A^{-1} =  \frac{1}{9} \left[\begin{array}{r}                           
7        &{    -3    } &{    2    }    \\
3        &{    0    } &{    -3    }    \\
-1        &{    3    } &{   1    }    \\
\end{array}\right]$

9. Use matrix multiplication to find A⁻¹B.
• We get: X = A⁻¹ B =
$ \frac{1}{9} \left[\begin{array}{r}                           
7        &{    -3    } &{    2    }    \\
3        &{    0    } &{    -3    }    \\
-1        &{    3    } &{   1    }    \\
\end{array}\right]~\left[\begin{array}{r}                           
6        \\
11        \\
0        \\
\end{array}\right]~ = \left[\begin{array}{r}                        1        \\
2        \\
3        \\
\end{array}\right]
$

10. So the solution is: x = 1, y = 2 and z = 3

---

The link below gives a few more solved examples:

Exercise 20.6

---

In the next section, we will see some miscellaneous examples.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com

20.14 - Applications of Determinants and Matrices

In the previous section, we saw adjoint and inverse of a matrix. In this section, we will see applications of determinants and matrices.

• First we will see consistent and inconsistent systems. It can be explained in 4 steps:

1. Consider a system of linear equations:
x + 2y = 4
2x + 3y = 5
(Recall that, in a linear equation, all variables will have a power of 1. If one or more variables have power greater that 1, it is a non-linear equation)
• Solving this system, we get: x = -2 and y = 3
• (-2, 3) is the only possible solution.
• If we draw the graphs of the given equations, we will get two lines. Those two lines will intersect at one and only one point (-2,3)
• The solution (-2,3) will satisfy both the equations.
2. Consider another system of linear equations:
6x - 2y = 16
3x - y = 8
• If we draw the graphs of these equations, we will see that, both the equations represent the same line.
• Any point which lies on one line will lie on the other line also.
• So any solution which satisfy one equation will satisfy the other equation also.
   ♦ For example, (3,1) satisfies both equations.
   ♦ Another example is (0,8).
• In this way, there will be an infinite number of solutions.
3. Consider yet another system of linear equations:
5x - y = 4
5x - y = -6
• If we draw the graphs of these equations, we will see that, they represent parallel lines.
• Parallel lines never meet. So this system has no solution.
4. We have seen three types of systems.
◼ Types I and II fall in the group: Consistent systems
• We can write:
If the system of equations have one or more than one solutions, it is a consistent system.
◼ Type III falls in the group: Inconsistent systems.
• We can write:
If the system of equations have no solution, it is a inconsistent system.

---

Determinants and matrices can be used to solve systems of linear equations. It can be explained in 5 steps:
1. Consider the system of equations
a₁ x +  b₁ y +  c₁ z = d₁
a₂ x +  b₂ y +  c₂ z = d₂
a₃ x +  b₃ y +  c₃ z = d₃

2. Let
$A = \left[\begin{array}{r}                           
a_1    &{    b_1    }    &{    c_1    }    \\
a_2    &{    b_2    }    &{    c_2    }    \\
a_3    &{    b_3    }    &{    c_3    }    \\
\end{array}\right],~X = \left[\begin{array}{r}       
x        \\
y        \\
z        \\
\end{array}\right]~~ \text{and}~~B = \left[\begin{array}{r}                           
d_1        \\
d_2        \\
d_3        \\
\end{array}\right]
$

3. Then the system of equations in (1) can be written as:
$\left[\begin{array}{r}                           
a_1    &{    b_1    }    &{    c_1    }    \\
a_2    &{    b_2    }    &{    c_2    }    \\
a_3    &{    b_3    }    &{    c_3    }    \\
\end{array}\right]~\left[\begin{array}{r}                           
x        \\
y        \\
z        \\
\end{array}\right]~ = \left[\begin{array}{r}                        d_1        \\
d_2        \\
d_3        \\
\end{array}\right]
$

• Consider the L.H.S
   ♦ A is  3 × 3 matrix. X is a 3 × 1 matrix.
   ♦ So multiplying A and X will give a 3 × 1 matrix.
• In the R.H.S also, we have a 3 × 1 matrix. So after multiplication, we will be able to equate corresponding terms.
• By equating corresponding terms, we will get the same system as in (1).
• Thus it is clear that, the given system can be written as
AX = B
4. If we can find the matrix X, we will be able to write the values of x, y and z.
• So our next task is to find X. For that, we adopt the following method:

◼ Remarks:
• 2 (magenta color): Here we premultiply the whole equation by A⁻¹ .
• 3 (magenta color): Here we use the fact that, A⁻¹A = I.
• 4 (magenta color): Here we use the fact that, IX = X.

5. We will be able to write the steps in (4), only if A⁻¹ exists. That is., A must be a non-singular matrix.
• If A is singular, we must calculate (adj A) B. Here two cases can arise.
I. (adj A) B ≠ O.
• Then the system is inconsistent.
II. (adj A) B = O.
• Then the system can be consistent or inconsistent.
   ♦ Consistent if there are infinite number of solutions.
   ♦ Inconsistent if there is no solution.

---

Let us see a solved example:

Solved example 20.23
Solve the system of equations:
x + 2y = 4
2x + 3y = 5
Solution:
1. The given system can be written in the form AX = B.
$A = \left[\begin{array}{r}                           
1        &{    2    }    \\
2        &{    3    }    \\
\end{array}\right],~X = \left[\begin{array}{r}       
x        \\
y        \\
\end{array}\right]~~ \text{and}~~B = \left[\begin{array}{r}                           
4        \\
5        \\
\end{array}\right]
$

2. So X = A⁻¹ B.
• Check whether A⁻¹ exists:
   ♦ |A| = (3 − 4) = −1
   ♦ |A| ≠ 0
   ♦ So A is a non-singular matrix. Therefore, A⁻¹ exists.

3. Use the method in Solved example 20.21 to find A⁻¹.
We get: $A^{-1} = \left[\begin{array}{r}                           
-3        &{    2    }    \\
2        &{    -1    }    \\
\end{array}\right]$

4. Use matrix multiplication to find A⁻¹B.
• We get: X = A⁻¹ B =
$\left[\begin{array}{r}                           
-3        &{    2    }    \\
2        &{    -1    }    \\
\end{array}\right]~\left[\begin{array}{r}                           
4        \\
5        \\
\end{array}\right]~ = \left[\begin{array}{r}                        -2        \\
3        \\
\end{array}\right]
$

5. So the solution is: x = -2 and y = 3

---

In the next section, we will see a few more solved examples.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com

20.13 - Solved Examples

In the previous section, we saw adjoint and inverse of a matrix. In this section, we will see some solved examples.

Solved example 20.20
If $A~=~\left [\begin{array}{r}   
1       &{    3    } &{    3    }    \\
1       &{    4    } &{    3    }    \\
1       &{    3    } &{    4    }    \\
\end{array}\right ]$, then verify that A(adj A) = |A| I. Also find A⁻¹.
Solution:
Part (i):
1. First we will find the Minors and Cofactors of A.

2. So the Cofactor matrix of A is: $\left [\begin{array}{r}   
7       &{    -1    } &{    -1    }    \\
-3       &{    1    } &{    0    }    \\
-3       &{    0    } &{    1    }    \\
\end{array}\right ]$

3. Transpose of the Cofactor matrix will give the adjoint matrix. So we get:

adj A = $\left [\begin{array}{r}   
7       &{    -3    } &{    -3    }    \\
-1       &{    1    } &{    0    }    \\
-1       &{    0    } &{    1    }    \\
\end{array}\right ]$

4. Use matrix multiplication to find A(adj A). We get:

$\left [\begin{array}{r}   
1       &{    3    } &{    3    }    \\
1       &{    4    } &{    3    }    \\
1       &{    3    } &{    4    }    \\
\end{array}\right ] \left [\begin{array}{r}   
7       &{    -3    } &{    -3    }    \\
-1       &{    1    } &{    0    }    \\
-1       &{    0    } &{    1    }    \\
\end{array}\right ] ~=~\left [\begin{array}{r}   
1       &{    0    } &{    0    }    \\
0       &{    1    } &{    0    }    \\
0       &{    0    } &{    1    }    \\
\end{array}\right ]$

5. Let us calculate |A|:

|A| = 1(16 − 9) − 3(4 − 3) + 3(3 − 4)
= 7 − 3 − 3 = 1

6. Now we can calculate |A|I:

$(1) \left [\begin{array}{r}   
1       &{    0    } &{    0    }    \\
0       &{    1    } &{    0    }    \\
0       &{    0    } &{    1    }    \\
\end{array}\right ] ~=~\left [\begin{array}{r}   
1       &{    0    } &{    0    }    \\
0       &{    1    } &{    0    }    \\
0       &{    0    } &{    1    }    \\
\end{array}\right ]$

7. From (4) and (6), we see that: A(adj A) = |A| I

Part (ii):
We have already calculated |A| and (adj A) in part (i). So we can calculate A⁻¹ as follows:

$A^{-1} = \frac{1}{|A|}(\text{adj A}) = \frac{1}{1} \left [\begin{array}{r}   
7       &{    -3    } &{    -3    }    \\
-1       &{    1    } &{    0    }    \\
-1       &{    0    } &{    1    }    \\
\end{array}\right ]= \left [\begin{array}{r}   
7       &{    -3    } &{    -3    }    \\
-1       &{    1    } &{    0    }    \\
-1       &{    0    } &{    1    }    \\
\end{array}\right ]$

Solved example 20.21
If $A~=~\left [\begin{array}{r}   
2        &{    3    }    \\
1        &{    -4    }    \\
\end{array}\right ]$ and $B~=~\left [\begin{array}{r}   
1        &{    -2    }    \\
-1        &{    3    }    \\
\end{array}\right ]$, then verify that (AB)⁻¹ = B⁻¹A⁻¹.
Solution:
1. First we will test whether A and B are invertible.
(i) |A| = −8 − 3 = −11
|A| ≠ 0. So A is invertible.
(ii) |B| = 3-2 = 1
|B| ≠ 0. So B is invertible.

2. Next we will find A⁻¹.
• adj A =  $\left [\begin{array}{r}   
-4        &{    -3    }    \\
-1        &{    2    }    \\
\end{array}\right ]$
(Recall the shortcut method explained in fig.20.5 of the previous section)

• So we get:
$A^{-1} = \frac{1}{|A|}(\text{adj A}) = -{\frac{1}{11}} \left [\begin{array}{r}   
-4        &{    -3    }    \\
-1        &{    2    }    \\
\end{array}\right ]$   

3. Next we will find B⁻¹.
• adj B =  $\left [\begin{array}{r}   
3        &{    2    }    \\
1        &{    1    }    \\
\end{array}\right ]$
(Recall the shortcut method explained in fig.20.5 of the previous section)
• So we get:
$B^{-1} = \frac{1}{|B|}(\text{adj B}) = \frac{1}{1} \left [\begin{array}{r}   
3        &{    2    }    \\
1        &{    1    }    \\
\end{array}\right ]= \left [\begin{array}{r}   
3        &{    2    }    \\
1        &{    1    }    \\
\end{array}\right ]$

4. Use matrix multiplication to find B⁻¹A⁻¹. We get:
$B^{-1} A^{-1} = \left [\begin{array}{r}   
3        &{    2    }    \\
1        &{    1    }    \\
\end{array}\right ]~\times~ -{\frac{1}{11}} \left [\begin{array}{r}   
-4        &{    -3    }    \\
-1        &{    2    }    \\
\end{array}\right ] = {\frac{1}{11}} \left [\begin{array}{r}   
14        &{    5    }    \\
5        &{    1    }    \\
\end{array}\right ]$

5. Use matrix multiplication to find AB. We get:
$AB = \left [\begin{array}{r}   
2        &{    3    }    \\
1        &{    -4    }    \\
\end{array}\right ]~\left [\begin{array}{r}   
1        &{    -2    }    \\
-1        &{    3    }    \\
\end{array}\right ] = \left [\begin{array}{r}   
-1        &{    5    }    \\
5        &{    -14    }    \\
\end{array}\right ]$

6. Next we will find |(AB)|.
|(AB)| = 14 − 25 = -11

7. Now we can calculate (AB)⁻¹.
• adj (AB) =  $\left [\begin{array}{r}   
-14        &{    -5    }    \\
-5        &{    -1    }    \\
\end{array}\right ]$
(Recall the shortcut method explained in fig.20.5 of the previous section)

• So we get:
$(AB)^{-1} = \frac{1}{|(AB)|}(\text{adj (AB)}) = \frac{1}{(-11)} \left [\begin{array}{r}   
-14        &{    -5    }    \\
-5        &{    -1    }    \\
\end{array}\right ] = \frac{1}{11} \left [\begin{array}{r}   
14        &{    5    }    \\
5        &{    1    }    \\
\end{array}\right ]$

8. Comparing the results in (4) and (7), we can write:
(AB)⁻¹ = B⁻¹A⁻¹.

Solved example 20.22
Show that the matrix   $A~=~\left [\begin{array}{r}   
2        &{    3    }    \\
1        &{    2    }    \\
\end{array}\right ]$ satisfies the equation A² − 4A + I = O, where I is 2 × 2 identity matrix and O is 2 × 2 zero matrix. Using this equation, find A⁻¹.
Solution:
Part (i): To prove that, A² − 4A + I = O
1. Use matrix multiplication to find A². We get:
$A^2 = AA = \left [\begin{array}{r}   
2        &{    3    }    \\
1        &{    2    }    \\
\end{array}\right ]~\left [\begin{array}{r}   
2        &{    3    }    \\
1        &{    2    }    \\
\end{array}\right ] = \left [\begin{array}{r}   
7        &{    12    }    \\
4        &{    7    }    \\
\end{array}\right ]$

2. Next we will find 4A.
$4A = 4 \left [\begin{array}{r}   
2        &{    3    }    \\
1        &{    2    }    \\
\end{array}\right ]= \left [\begin{array}{r}   
8        &{    12    }    \\
4        &{    8    }    \\
\end{array}\right ]$

3. Substituting the above matrices in the given equation, we get:

• We see that, L.H.S = R.H.S.
• So matrix A satisfies the given equation.

Part (ii): To find A⁻¹.
1. First we need to test whether A is invertible.
• We have: |A| = (4-3) = 1.
• Since |A| ≠ 0, A is invertible.

2. To find A⁻¹, we rearrange the equation that was proved in part (i).

◼ Remarks:
• 3 (magenta color): In this line, we post multiply the whole equation by A⁻¹.
• 4 (magenta color): In this line, we apply the fact that, AA⁻¹ = I.

---

The link below gives a few more solved examples:

Exercise 20.5

---

In the next section, we will see the applications of determinants and matrices.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com

20.12 - Adjoint And Inverse of A Matrix

In the previous section, we saw Minors and Cofactors. In this section, we will see adjoint and inverse of a matrix.

Adjoint of a Matrix

Some basics can be written in 6 steps:
1. Consider a square matrix A = [a_ij]_n.
2. We know how to write the Cofactor A_ij of any element a_ij of the matrix A.
3. So we can write a new matrix which contains the Cofactors.
• For example, if the original matrix is
$A ~=~\left [\begin{array}{r}                           
a_{11}      &{    a_{12}    } &{    a_{13}    }    \\
a_{21}      &{    a_{22}    } &{    a_{23}    }    \\
a_{31}      &{    a_{32}    } &{    a_{33}    }    \\
\end{array}\right ]$,
then the corresponding matrix of Cofactors will be:
$\left [\begin{array}{r}                           
A_{11}      &{    A_{12}    } &{    A_{13}    }    \\
A_{21}      &{    A_{22}    } &{    A_{23}    }    \\
A_{31}      &{    A_{32}    } &{    A_{33}    }    \\
\end{array}\right ]$

4. Now, the transpose of the matrix of Cofactors will be:
$\left [\begin{array}{r}                           
A_{11}      &{    A_{21}    } &{    A_{31}    }    \\
A_{12}      &{    A_{22}    } &{    A_{32}    }    \\
A_{13}      &{    A_{23}    } &{    A_{33}    }    \\
\end{array}\right ]$
• This matrix obtained by transposing, is called adjoint matrix.
5. Adjoint of matrix A is denoted by adj A.
6. For the example matrix A mentioned in (3),
adj A = $\left [\begin{array}{r}                           
A_{11}      &{    A_{21}    } &{    A_{31}    }    \\
A_{12}      &{    A_{22}    } &{    A_{32}    }    \\
A_{13}      &{    A_{23}    } &{    A_{33}    }    \\
\end{array}\right ]$

Solved example 20.19
Find adj A for $A~=~\left [\begin{array}{r}   
2       &{    5    }    \\
-3       &{    7    }    \\
\end{array}\right ]$
Solution:
1. First we will find the Minors and Cofactors:

2. So the matrix of Cofactors is:
$\left [\begin{array}{r}   
7       &{    3    }    \\
-5       &{    2    }    \\
\end{array}\right ]$

3. The transpose of the above matrix, is the required adjoint matrix. So we get:

$\text{adj A}~=~\left [\begin{array}{r}   
7       &{    -5    }    \\
3       &{    2    }    \\
\end{array}\right ]$

---

For any square matrix of order 2, there is a direct method to find the adjoint. It can be written in 4 steps:
1. Fig.20.5(a) below shows the original matrix A.

Fig.20.5

2. Consider the yellow diagonal, which is drawn from left-top to right-bottom. We need to interchange the elements in this diagonal.   
3. Consider the red diagonal, which is drawn from right-top to left-bottom. We should not interchange the elements in this diagonal. But we must change the signs of those elements.
4. The resulting new matrix is the adj A. It is shown in fig.20.5(b) above.

---

Now we will see four theorems related to adjoint matrices.

Theorem I
• If A is any given square matrix of order n, then
A(adj A) = (adj A)A = |A|I
    ♦ Where I is the identity matrix of the same order n.

Verification can be written in steps:
1. Let $A ~=~\left [\begin{array}{r}                           
a_{11}      &{    a_{12}    } &{    a_{13}    }    \\
a_{21}      &{    a_{22}    } &{    a_{23}    }    \\
a_{31}      &{    a_{32}    } &{    a_{33}    }    \\
\end{array}\right ]$.
• Then adj A will be: $\left [\begin{array}{r}       
A_{11}      &{    A_{21}    } &{    A_{31}    }    \\
A_{12}      &{    A_{22}    } &{    A_{32}    }    \\
A_{13}      &{    A_{23}    } &{    A_{33}    }    \\
\end{array}\right ]$
2. We know how to write the product A(adj A).
• Let us write the first element (intersection of R₁ and C₁):
a₁₁ A₁₁ + a₁₂ A₁₂ + a₁₃ A₁₃
• We see that:
    ♦ First term is the product of a₁₁ and it’s Cofactor.
    ♦ Second term is the product of a₁₂ and it’s Cofactor.
    ♦ Third term is the product of a₁₃ and it’s Cofactor.            
    ♦ Also, we are taking the sum of the three terms.
3. So we can write:
The first element in A(adj a) is: The determinant |A|
4. All diagonal elements of A(adj a), will be similar to the form written in (2).
• So all diagonal elements in A(adj a), will become |A|
5. Let us write the second element (intersection of R₁ and C₂) of A(adj a):
a₁₁ A₂₁ + a₁₂ A₂₂ + a₁₃ A₂₃
• We see that:
    ♦ First term is the product of a₁₁ and a different Cofactor.
    ♦ Second term is the product of a₁₂ and a different Cofactor.
    ♦ Third term is the product of a₁₃ and a different Cofactor.
    ♦ Also, we are taking the sum of the three terms.
6. So we can write:
The second element in A(adj a) is: zero
7. All non-diagonal elements of A(adj a), will be similar to the form written in (5).
• So all non-diagonal elements in A(adj a), will become zero.
8. Thus we get:
$A(\text{adj A})~=~\left[\begin{array}{r}   
|A|    &{    0    }    &{    0    }    \\
0    &{    |A|    }    &{    0    }    \\
0    &{    0    }    &{    |A|    }    \\
\end{array}\right]
~=~|A|\left[\begin{array}{r}                           
1    &{    0    }    &{    0    }    \\
0    &{    1    }    &{    0    }    \\
0    &{    0    }    &{    1    }    \\
\end{array}\right]~=~|A|I$
9. Similarly, we can show that (adj A)A = |A|I
10. Based on (8) and (9), we can write:
A(adj A) = (adj A) A = |A|I

Theorem II
If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.
(We will see the proof of this theorem in higher classes)
    ♦ A square matrix A is said to be singular if |A| = 0
    ♦ A square matrix A is said to be non-singular if |A| ≠ 0

Theorem III
If A and B are square matrices of the same order, then |AB| = |A| |B|.
(We will see the proof of this theorem in higher classes)

---

Now we can write about an interesting result. It can be written in 4 steps:

1. Let A be a square matrix of order 3.
2. Let us try to simplify (adj A)A: 

◼ Remarks:
• 1 (magenta color): Here we use theorem I
• 2 (magenta color): In the R.H.S, the unit matrix is multiplied by a constant value. So all non-diagonal elements of the resulting matrix will be zeroes.
• 3 (magenta color): Here we take determinants on both sides.
• 5 (magenta color): Here we apply theorem III in the L.H.S.

3. We see that:
• We started the calculations with a square matrix A of order 3.
• In the final result, the determinant of A has a power of 2.
4. So we can write the general form:
If A is a square matrix of order n, then
|(adj a)| = |A|^n-1.
(We will see the actual proof in higher classes)

---

Theorem IV
A square matrix A is invertible if and only if A is a non-singular matrix.
• Proof can be written in 3 steps:
1. Let A be a invertible matrix of order n. Also, let I be an identity matrix of the same order n.
• Then, from the discussion that we had on matrices in the previous chapter, we can write: AB = BA = I.
    ♦ Where B is a square matrix of order n.
2. Consider the equation AB = I
• Writing determinants of matrices on both sides, we get:
|AB| = |I|
• This is same as |AB| = 1
3. Applying theorem III on the L.H.S, we get: |A| |B| = 1.
• |A| and |B| are numbers. If their product is 1, it means that, none of them can be zero.
• So we get: |A| ≠ 0.
• That means, A is a non-singular matrix.

Converse of Theorem IV
If A is a non-singular square matrix, then it is invertible.
• Proof can be written in 3 steps:
1. Consider theorem I:
A(adj A) = (adj A) A = |A|I
2. |A| is a number. So we can use it to divide the whole equation. We get:
$A \left(\frac{1}{|A|}(\text{adj A}) \right)~=~ \left(\frac{1}{|A|}(\text{adj A}) \right)A~=~I$
3. We can rearrange this equation into a familiar form, if we put 'B' in the place of $\frac{1}{|A|}(\text{adj A})$.
• We get: AB = BA = I
4. The above result implies that, matrix B is the inverse of matrix A.
• So we can write:
A is invertible and the inverse is $\frac{1}{|A|}(\text{adj A})$

---

In the next section, we will see some solved examples.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com

20.11 - Minors And Cofactors

In the previous section, we saw area of triangles. In this section, we will see Minors and Cofactors.

Minors

Some basics about Minors can be written in 6 steps:
1. Consider a determinant.
2. Pick any element a_ij from that determinant.
3. Delete one row and one column:
   ♦ Delete the row in which a_ij is situated (the i^th row)
   ♦ Delete the column in which a_ij is situated (the j^th column)
4. After deleting the above row and column, we get a new determinant.
• This new determinant is called the Minor of a_ij
5. Minor of a_ij is denoted by M_ij.
6. Since one row and one column are being deleted from the original determinant, we can write a useful point. It can be written in 2 steps:
(i) Consider any determinant of order n, where n≥2.
(ii) We know how to write the Minor of any element of that determinant. All those Minors will be of the order (n-1).
(iii) We cannot consider determinants whose order is less than 2. This is because, in such determinants, there will be only one element. It is not possible to find the Minor of that single element.

---

Now we will see a solved example:

Solved example 20.15
Find the Minor of the element 8 in the determinant:
$\Delta~=~\left |\begin{array}{r}                           
3    &{    5    }    &{    9    }    \\
6    &{    11    }    &{    8    }    \\
7    &{    15    }    &{    12    }    \\
\end{array}\right |$
Solution:
1. The element 8 is in the second row and third column.
2. So we delete the second row and third column.
3. The new determinant thus obtained is:
$\left |\begin{array}{r}                           
3      &{    5    }    \\
7      &{    15    }    \\
\end{array}\right |$ 
3. The value of this new determinant is:
(3 × 15 - 7 × 5) = (45 - 35) = 10
4. So we can write:
• In the original determinant,
The Minor of element 8 = M₂₃ = 10

---

Cofactors

This can be explained in 2 steps:
1. If M_ij is the Minor of the element a_ij, then
the Cofactor of a_ij can be obtained simply by multiplying (-1)^i+j and M_ij.
2. The Cofactor of a_ij is denoted by A_ij.
• So we can write:
A_ij = (−1)^i+j M_ij

---

Let us see some solved examples:

Solved example 20.16
Find the Minors and Cofactors of all the elements of the determinant:
$\left |\begin{array}{r}                           
1      &{    -2    }    \\
4      &{    3    }    \\
\end{array}\right |$ 
Solution:
1. M₁₁ = 3
• So A₁₁ = (−1)¹⁺¹ M₁₁ = (−1)² (3) = 3

2. M₁₂ = 4
• So A₁₂ = (−1)¹⁺² M₁₂ = (−1)³ (4) = −4

3. M₂₁ = −2
• So A₁₂ = (−1)²⁺¹ M₁₂ = (−1)³ (−2) = 2

4. M₂₂ = 1
• So A₂₂ = (−1)²⁺² M₂₂ = (−1)⁴ (1) = 1

Solved example 20.17
Find the Minors and Cofactors of a₁₁ and a₂₁ in the determinant:
$\left |\begin{array}{r}                           
a_{11}      &{    a_{12}    } &{    a_{13}    }    \\
a_{21}      &{    a_{22}    } &{    a_{23}    }    \\
a_{31}      &{    a_{32}    } &{    a_{33}    }    \\
\end{array}\right |$ 
Solution:
1. M₁₁ =
$\left |\begin{array}{r}                           
a_{22}      &{    a_{23}    }    \\
a_{32}      &{    a_{33}    }    \\
\end{array}\right |~=~a_{22} a_{33} \,-\, a_{23} a_{32}$ 
• So A₁₁ = (−1)¹⁺¹ M₁₁ =
$(-1)^2 (a_{22} a_{33} \,-\, a_{23} a_{32})~=~a_{22} a_{33} \,-\, a_{23} a_{32}$

2. M₂₁ =
$\left |\begin{array}{r}                           
a_{12}      &{    a_{13}    }    \\
a_{32}      &{    a_{33}    }    \\
\end{array}\right |~=~a_{12} a_{33} \,-\, a_{13} a_{32}$ 
• So A₂₁ = (−1)²⁺¹ M₂₁ =
$(-1)^3 (a_{12} a_{33} \,-\, a_{13} a_{32})~=~- a_{12} a_{33} \,+\, a_{13} a_{32}$

---

Now we know the basics about Minors and Cofactors. So we can learn about a method which will help us to write the determinant in a compact form. It can be written in 7 steps:

1. Consider the determinant:
$\Delta ~=~\left |\begin{array}{r}                           
a_{11}      &{    a_{12}    } &{    a_{13}    }    \\
a_{21}      &{    a_{22}    } &{    a_{23}    }    \\
a_{31}      &{    a_{32}    } &{    a_{33}    }    \\
\end{array}\right |$

2. We know that:
$\Delta = a_{11} \times (-1)^{1+1} \times \left |\begin{array}{r}                           
a_{22}      &{    a_{23}    }    \\
a_{32}      &{    a_{33}    }    \\
\end{array}\right |~+~a_{12} \times (-1)^{1+2} \times \left |\begin{array}{r}                           
a_{21}      &{    a_{23}    }    \\
a_{31}      &{    a_{33}    }    \\
\end{array}\right |~+~a_{13} \times (-1)^{1+3} \times \left |\begin{array}{r}                           
a_{21}      &{    a_{22}    }    \\
a_{31}      &{    a_{32}    }    \\
\end{array}\right |$

3. We can write this in terms of Cofactors.
• Consider the first term in the R.H.S of (2). This term is: a₁₁  × A₁₁
• Consider the second term in the R.H.S of (2). This term is: a₁₂  × A₁₂
• Consider the third term in the R.H.S of (2). This term is: a₁₃  × A₁₃

4. So the result in (2) becomes:
$\Delta~=~a_{11} A_{11}~+~a_{12} A_{12}~+~a_{13} A_{13}$
• Thus we are able to write Δ in a compact form.

5. The method used in (4) is applicable for any row or any column. For example:
• Expanding along the second row, we can write:
$\Delta~=~a_{21} A_{21}~+~a_{22} A_{22}~+~a_{23} A_{23}$
• Expanding along the third column, we can write:
$\Delta~=~a_{13} A_{13}~+~a_{23} A_{23}~+~a_{33} A_{33}$

6. So the determinant can be calculated in 3 simple steps:
(i) Take any row (or any column)
(ii) Multiply each element of that row (or column) with the corresponding Cofactor.
(iii) Find the sum of the "products obtained in (ii)". This sum is the determinant.

7. Consider the step 6(ii) written above. It is important to use the corresponding Cofactors. If we use the Cofactors of any other row or column, the sum will become zero.

• Let us see an example. It can be written in 4 steps:
(i) Let us pick the first row for expansion. But the Cofactors used are from the second row.
(ii) Then the sum is:
$a_{11} A_{21}~+~a_{12} A_{22}~+~a_{13} A_{23}$
(iii) This can be expanded as:
$a_{11} (-1)^{2+1} (a_{12} a_{33} - a_{13} a_{32})$
$+~ a_{12} (-1)^{2+2} (a_{11} a_{33} - a_{13} a_{31})$
$+~ a_{13} (-1)^{2+3} (a_{11} a_{32} - a_{12} a_{31})$
(iv) This is same as:
$-a_{11} a_{12} a_{33} + a_{11} a_{13} a_{32}$
$+~ a_{12} a_{11} a_{33} - a_{12} a_{13} a_{31}$
$-~ a_{13} a_{11} a_{32} + a_{13} a_{12} a_{31}~=~0$

---

Solved example 20.18
Find the Minors and Cofactors of elements of the determinant:
$\left |\begin{array}{r}                           
8      &{    3    } &{    0    }    \\
-5      &{    11    } &{    -2    }    \\
6      &{    0    } &{    -7    }    \\
\end{array}\right |$
And verify that a₁₁ A₃₁ + a₁₂ A₃₂  + a₁₃ A₃₃ = 0   
Solution:

• Now we can verify the given statement:
a₁₁ A₃₁ + a₁₂ A₃₂  + a₁₃ A₃₃
= 8(-6) + 3(16) + 0(-47)
= -48 + 48 + 0
= 0

---

The link below gives a few more solved examples:

Exercise 20.4

---

In the next section, we will see adjoint and inverse of a matrix.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com

20.10 - Area of A Triangle

In the previous section, we saw some solved examples related to properties of determinants. In this section, we will see area of triangles.

Some basics can be written in 3 steps:
1. In our earlier coordinate geometry classes, we have seen an expression to find the area of any triangle:

$\text{Area} = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
(Details here)

2. Now consider the determinant:

$\Delta = \frac{1}{2} \left|\begin{array}{r}      
x_1    &{    y_1    }    &{    1    }    \\
x_2    &{    y_2    }    &{    1    }    \\
x_3    &{    y_3    }    &{    1    }    \\
\end{array}\right|$
• If we expand this determinant along the first column, we will get the same expression as in (1).

3. That means, area of a triangle can be written in "determinant form" also.
• But it is important to take the absolute value of the determinant. This is because, area cannot be a negative quantity.

---

Now we will see some solved examples.

Solved example 20.13
Find the area of the triangle whose vertices are (-1.5,2), (-2.5,-2), (4,1.5)
Solution:

◼ Remarks:
• 3: Here we apply two operations:
   ♦ R₁ → R₁ − R₃.
   ♦ R₂ → R₂ − R₃.
4: Here we expand the determinant along C₃.

Solved example 20.14
Find the equation of the line joining A(1,3) and B(0,0) using determinants and find k if D(k,0) is a point such that area of triangle ABD is 3 sq units.
Solution:
Part (i):
1. Let P(x,y) be any point on the line AB.
Then area of the triangle APB = 0. This is because, three collinear points cannot form a triangle.
2. So we can write:

◼ Remarks:
• 2 (magenta color): Here we expand the determinant along the second row.
• 3 (magenta color): Here we use the index (2+3). This is because, '1' is the a₂₃^th element.

3. Since the area is zero, we can write:
-(1/2)(y-3x) = 0
• From this we get: -y + 3x = 0
• Which is same as: y = 3x

4. The line y=3x will pass through both A(1,3) and B(0,0).

Part (ii):

◼ Remarks:
• 2 (magenta color): Here we write $\pm 3$ because, the value of the determinant can be either +3 or -3. We can ignore the -ve sign only when we write it as an area.
• 3 (magenta color): Here we expand the determinant along the second row.
• 3 (magenta color): Here we use the index (2+3). This is because, '1' is the a₂₃^th element.

◼ We can write:
• Area of the triangle formed by the three points A(1,3), B(0,0) and D(2,0) is 3 units.
• Area of the triangle formed by the three points A(1,3), B(0,0) and D(-2,0) is also 3 units. 

---

The link below gives a few more solved examples:

Exercise 20.3

---

In the next section, we will see Minors and Cofactors.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com

20.9 - Solved Examples

In the previous section, we completed the discussion on properties of determinants. In this section, we will see some solved examples.

Solved example 20.8
Without expanding, prove that

Solution:

 

◼ Remarks:
• 2 (magenta color): Here we apply property VI
• 3(magenta color):
   ♦ Consider R₁ and R₃. Take any two corresponding elements from them.
   ♦ The element from R₁ will be proportional to the element from R₃ in the ratio (x+y+z) : 1.
   ♦ So value of the determinant is zero.

Solved example 20.9
Evaluate

Solution:

◼ Remarks:
• 2 and 3 (magenta color): Here we apply property VI
• 5(magenta color): Here we expand along C₁.

Solved example 20.10
Prove that

Solution:

1. Split the given determinant as |A| + |B| by applying property V.

◼ Remarks:
• 2 (magenta color): Here we apply property V and split Δ into |A| and |B|.
• 3 (magenta color): Here we apply property V and split |A|.
• 5(magenta color): Line 4 has four determinants.
   ♦ First is expanded along R₁.
   ♦ Second is expanded along R₃.
   ♦ Third is expanded along R₂.
   ♦ Fourth is expanded along C₁.

2. Evaluate |B|:

◼ Remarks:

• 2 (magenta color): Here we apply property V and split |B|.
• 3 (magenta color): Line 2 has two determinants.
   ♦ First is expanded along R₁.
   ♦ Second is expanded along R₁.

3. Find the sum:
Δ = |A| + |B|
= 3abc - a²c - ac² + ac² + a²c + abc
= 4abc

Solved example 20.11
If x, y, z are different and

then show that 1 + xyz = 0
Solution:
1. Split the given determinant as |A| + |B| by applying property V.

◼ Remarks:
• 2 (magenta color): Here we apply property V and split Δ into |A| and |B|.
• 3 (magenta color): Here we simplify |A|.
• 6(magenta color): Here we expand the determinant along C₃.

2. Evaluate |B|:

◼ Remarks:

• 2 (magenta color): Here we apply property IV and take out the common factors x, y and z.
• 3 (magenta color): Here we apply property II and interchange C₁ and C₂. So the sign of the determinant will change.
• 4 (magenta color): Here we apply property II and interchange C₂ and C₃. So the sign of the determinant will change again.
• 5 (magenta color):
Line 4 has a determinant on the R.H.S. This determinant is |A|.

3. Find the sum:
Δ = |A| + |B|
= |A| + xyz |A|
= (1+xyz)|A|
= (1+xyz)(x−z)(y−z)(y−x)

4. Given that Δ = 0.
• So we can write: (1+xyz)(x−z)(y−z)(y−x) = 0
• Also given that, x, y, z are different.
• So (x−z) ≠ 0, (y−z) ≠ 0, (y−x) ≠ 0
• Thus we get: 1+xyz = 0

Solved example 20.12
Show that

Solution:
1. Split the given determinant as |A| + |B| by applying property V.

◼ Remarks:

• 2 (magenta color): Here we apply property V and split Δ into |A| and |B|.
• 3 (magenta color): Here we apply property V and split |A|.
• 4 (magenta color): Line 3 has two determinants.
   ♦ The first has two identical columns. So by applying property III, it becomes zero.
• 5 (magenta color): Line 4 has a determinant. It is expanded along the second row.
• 8 (magenta color): |B| is expanded along the first row.

3. Find the sum:

◼ Remarks:
• 4 (magenta color): Here we take out abc as a common factor.

---

A few more Solved examples can be seen in the following video:

Exercise 20.2

---

In the next section, we will see Area of a triangle.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com

20.8 - Property VI

In the previous section, we saw the fifth property of determinants. In this section, we will see the sixth property.

Property VI
This can be written in 6 steps:
1. Let Δ = $\left |\begin{array}{c}                           
a_1     &{    a_2     }    &{    a_3     }    \\
b_1    &{    b_2    }    &{    b_3    }    \\
c_1    &{    c_2    }    &{    c_3    }    \\
\end{array}\right | $.
2. Pick any two rows, say R₂ and R₃.
Apply R₂ → R₂ + k R₃

• Then we get a new determinant Δ₁

Δ₁ = $\left |\begin{array}{c}                           
a_1     &{    a_2     }    &{    a_3     }    \\
b_1 + k c_1    &{    b_2 + k c_2    }    &{    b_3 + k c_2    }    \\
c_1    &{    c_2    }    &{    c_3    }    \\
\end{array}\right | $.

• Note that, when we apply R₂ → R₂ + k R₃, the row R₂ is affected. The other row R₃ remains the same.

3. We can apply property 5. That is., we can split Δ₁ and write it as the sum of two determinants:

$\left |\begin{array}{c}                           
a_1     &{    a_2     }    &{    a_3     }    \\
b_1 + k c_1    &{    b_2 + k c_2    }    &{    b_3 + k c_2    }    \\
c_1    &{    c_2    }    &{    c_3    }    \\
\end{array}\right | ~=~\left |\begin{array}{c}                           
a_1     &{    a_2     }    &{    a_3    }    \\
b_1    &{    b_2    }    &{    b_3    }    \\
c_1    &{    c_2    }    &{    c_3    }    \\
\end{array}\right |~+~\left |\begin{array}{c}                           
a_1     &{    a_2     }    &{    a_3    }    \\
k c_1    &{    k c_2    }    &{    k c_3    }    \\
c_1    &{    c_2    }    &{    c_3    }    \\
\end{array}\right |$

4. In the above equation, consider the second determinant in the R.H.S. All the elements of R₂ are proportional to the corresponding elements in R₃ in the same ratio k:1. So by applying property IV, this determinant is zero.

5. So the equation in (3) becomes:
$\left |\begin{array}{c}                           
a_1     &{    a_2     }    &{    a_3     }    \\
b_1 + k c_1    &{    b_2 + k c_2    }    &{    b_3 + k c_2    }    \\
c_1    &{    c_2    }    &{    c_3    }    \\
\end{array}\right | ~=~\left |\begin{array}{c}                           
a_1     &{    a_2     }    &{    a_3    }    \\
b_1    &{    b_2    }    &{    b_3    }    \\
c_1    &{    c_2    }    &{    c_3    }    \\
\end{array}\right |~+~0$

• That is: Δ₁ = Δ

6. We can write:
If we apply the operation R_i → R_i + k R_j, the value of the determinant remains same.
7. This is true for columns also. We can write:
If we apply the operation C_i → C_i + k C_j, the value of the determinant remains same.
8. When we apply R_i → R_i + k R_j, the row affected is R_i . The row R_j is not affected.
• In one step, we must not use R_i in another operation.
9. A rule similar to (8) can be written for columns also.

---

Now we have a clear understanding about property VI. Let us see an example.

• Show that $\left|\begin{array}{r}                           
a    &{    a+b    }    &{    a+b+c    }    \\
2a    &{    3a+2b    }    &{    4a+3b+2c    }    \\
3a    &{    6a+3b    }    &{    10a+6b+3c    }    \\
\end{array}\right|~=~a^3$.
Solution:
 

◼ Remarks:
• 2, 3 and 4 (magenta color): Here we apply property VI
• 5(magenta color): Here we expand along C₁

---

In the next section, we will see some solved examples.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com