In the previous section, we saw area of triangles. In this section, we will see Minors and Cofactors.
Minors
Some basics about Minors can be written in 6 steps:
1. Consider a determinant.
2. Pick any element aij from that determinant.
3. Delete one row and one column:
♦ Delete the row in which aij is situated (the ith row)
♦ Delete the column in which aij is situated (the jth column)
4. After deleting the above row and column, we get a new determinant.
•
This new determinant is called the Minor of aij
5. Minor of aij is denoted by Mij.
6. Since one row and one column are being deleted from the original determinant, we can write a useful point. It can be written in 2 steps:
(i) Consider any determinant of order n, where n≥2.
(ii) We know how to write the Minor of any element of that determinant. All those Minors will be of the order (n-1).
(iii) We cannot consider determinants whose order is less than 2. This is because, in such determinants, there will be only one element. It is not possible to find the Minor of that single element.
Now we will see a solved example:
Solved example 20.15
Find the Minor of the element 8 in the determinant:
$\Delta~=~\left |\begin{array}{r}
3 &{ 5 } &{ 9 } \\
6 &{ 11 } &{ 8 } \\
7 &{ 15 } &{ 12 } \\
\end{array}\right |$
Solution:
1. The element 8 is in the second row and third column.
2. So we delete the second row and third column.
3. The new determinant thus obtained is:
$\left |\begin{array}{r}
3 &{ 5 } \\
7 &{ 15 } \\
\end{array}\right |$
3. The value of this new determinant is:
(3 × 15 - 7 × 5) = (45 - 35) = 10
4. So we can write:
•
In the original determinant,
The Minor of element 8 = M23 = 10
Cofactors
This can be explained in 2 steps:
1. If Mij is the Minor of the element aij, then
the Cofactor of aij can be obtained simply by multiplying (-1)i+j and Mij.
2. The Cofactor of aij is denoted by Aij.
•
So we can write:
Aij = (−1)i+j Mij
Let us see some solved examples:
Solved example 20.16
Find the Minors and Cofactors of all the elements of the determinant:
$\left |\begin{array}{r}
1 &{ -2 } \\
4 &{ 3 } \\
\end{array}\right |$
Solution:
1. M11 = 3
•
So A11 = (−1)1+1 M11 = (−1)2 (3) = 3
2. M12 = 4
•
So A12 = (−1)1+2 M12 = (−1)3 (4) = −4
3. M21 = −2
•
So A12 = (−1)2+1 M12 = (−1)3 (−2) = 2
4. M22 = 1
•
So A22 = (−1)2+2 M22 = (−1)4 (1) = 1
Solved example 20.17
Find the Minors and Cofactors of a11 and a21 in the determinant:
$\left |\begin{array}{r}
a_{11} &{ a_{12} } &{ a_{13} } \\
a_{21} &{ a_{22} } &{ a_{23} } \\
a_{31} &{ a_{32} } &{ a_{33} } \\
\end{array}\right |$
Solution:
1. M11 =
$\left |\begin{array}{r}
a_{22} &{ a_{23} } \\
a_{32} &{ a_{33} } \\
\end{array}\right |~=~a_{22} a_{33} \,-\, a_{23} a_{32}$
•
So A11 = (−1)1+1 M11 =
$(-1)^2 (a_{22} a_{33} \,-\, a_{23} a_{32})~=~a_{22} a_{33} \,-\, a_{23} a_{32}$
2. M21 =
$\left |\begin{array}{r}
a_{12} &{ a_{13} } \\
a_{32} &{ a_{33} } \\
\end{array}\right |~=~a_{12} a_{33} \,-\, a_{13} a_{32}$
•
So A21 = (−1)2+1 M21 =
$(-1)^3 (a_{12} a_{33} \,-\, a_{13} a_{32})~=~- a_{12} a_{33} \,+\, a_{13} a_{32}$
Now we know the basics about Minors and Cofactors. So we can learn about a method which will help us to write the determinant in a compact form. It can be written in 7 steps:
1. Consider the determinant:
$\Delta ~=~\left |\begin{array}{r}
a_{11} &{ a_{12} } &{ a_{13} } \\
a_{21} &{ a_{22} } &{ a_{23} } \\
a_{31} &{ a_{32} } &{ a_{33} } \\
\end{array}\right |$
2. We know that:
$\Delta = a_{11} \times (-1)^{1+1} \times \left |\begin{array}{r}
a_{22} &{ a_{23} } \\
a_{32} &{ a_{33} } \\
\end{array}\right |~+~a_{12} \times (-1)^{1+2} \times \left |\begin{array}{r}
a_{21} &{ a_{23} } \\
a_{31} &{ a_{33} } \\
\end{array}\right |~+~a_{13} \times (-1)^{1+3} \times \left |\begin{array}{r}
a_{21} &{ a_{22} } \\
a_{31} &{ a_{32} } \\
\end{array}\right |$
3. We can write this in terms of Cofactors.
•
Consider the first term in the R.H.S of (2). This term is: a11 × A11
•
Consider the second term in the R.H.S of (2). This term is: a12 × A12
•
Consider the third term in the R.H.S of (2). This term is: a13 × A13
4. So the result in (2) becomes:
$\Delta~=~a_{11} A_{11}~+~a_{12} A_{12}~+~a_{13} A_{13}$
•
Thus we are able to write Δ in a compact form.
5. The method used in (4) is applicable for any row or any column. For example:
•
Expanding along the second row, we can write:
$\Delta~=~a_{21} A_{21}~+~a_{22} A_{22}~+~a_{23} A_{23}$
•
Expanding along the third column, we can write:
$\Delta~=~a_{13} A_{13}~+~a_{23} A_{23}~+~a_{33} A_{33}$
6. So the determinant can be calculated in 3 simple steps:
(i) Take any row (or any column)
(ii) Multiply each element of that row (or column) with the corresponding Cofactor.
(iii) Find the sum of the "products obtained in (ii)". This sum is the determinant.
7. Consider the step 6(ii) written above. It is important to use the corresponding Cofactors. If we use the Cofactors of any other row or column, the sum will become zero.
•
Let us see an example. It can be written in 4 steps:
(i) Let us pick the first row for expansion. But the Cofactors used are from the second row.
(ii) Then the sum is:
$a_{11} A_{21}~+~a_{12} A_{22}~+~a_{13} A_{23}$
(iii) This can be expanded as:
$a_{11} (-1)^{2+1} (a_{12} a_{33} - a_{13} a_{32})$
$+~ a_{12} (-1)^{2+2} (a_{11} a_{33} - a_{13} a_{31})$
$+~ a_{13} (-1)^{2+3} (a_{11} a_{32} - a_{12} a_{31})$
(iv) This is same as:
$-a_{11} a_{12} a_{33} + a_{11} a_{13} a_{32}$
$+~ a_{12} a_{11} a_{33} - a_{12} a_{13} a_{31}$
$-~ a_{13} a_{11} a_{32} + a_{13} a_{12} a_{31}~=~0$
Solved example 20.18
Find the Minors and Cofactors of elements of the determinant:
$\left |\begin{array}{r}
8 &{ 3 } &{ 0 } \\
-5 &{ 11 } &{ -2 } \\
6 &{ 0 } &{ -7 } \\
\end{array}\right |$
And verify that a11 A31 + a12 A32 + a13 A33 = 0
Solution:
• Now we can verify the given statement:
a11 A31 + a12 A32 + a13 A33
= 8(-6) + 3(16) + 0(-47)
= -48 + 48 + 0
= 0
The link below gives a few more solved examples:
In the next section, we will see adjoint and inverse of a matrix.
Copyright©2024 Higher secondary mathematics.blogspot.com
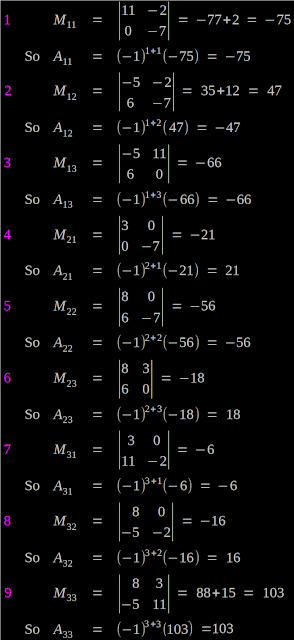
No comments:
Post a Comment