In the previous section, we saw the basic properties of an ellipse. In this section, we will see equation of an ellipse.
• To write the equation of an ellipse, we must first place it on the Cartesian plane.
• The equation will be in the simplest form when the following three conditions are satisfied:
♦ The center of the ellipse is at the origin O.
♦ The major axis of the ellipse lies along the x-axis.
♦ The minor axis of the ellipse lies along the y-axis.
• This is shown in fig.11.34 below:
 |
| Fig.11.34 |
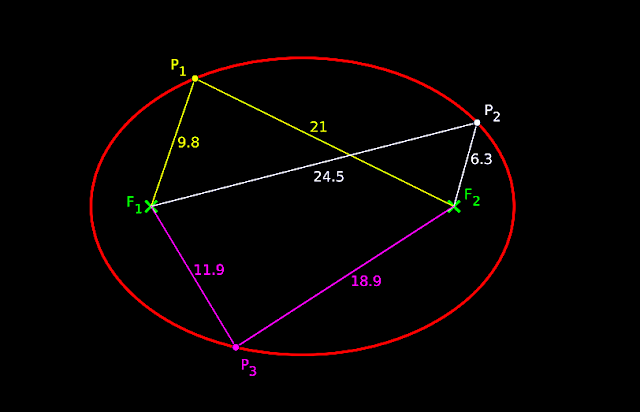
• Based on fig.11.34, we can derive the equation in 6 steps:
1. Let P(x,y) be any point on the ellipse.
2. We know that, F1 is at a distance of ‘c’ from O.
• So the coordinates of F1 will be (-c,0)
3. We know that, F2 is at a distance of ‘c’ from O.
• So the coordinates of F2 will be (c,0)
4. Now we have three points and their coordinates:
P(x,y), F1(-c,0), F2(c,0)
• Using the distance formula, we can write some distances:
• First we write the distance PF1:
$\begin{array}{ll}
{}&{PF_1}
& {~=~}& {\sqrt{(x~-~ -c)^2~+~(y - 0)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(x + c)^2~+~y^2}}
&{} \\
\end{array}$
• Next we write the distance PF2:
$\begin{array}{ll}
{}&{PF_2}
& {~=~}& {\sqrt{(x~-~ c)^2~+~(y - 0)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(x - c)^2~+~y^2}}
&{} \\
\end{array}$
• Sum of the above two distances is: $\sqrt{(x + c)^2~+~y^2}~+~\sqrt{(x - c)^2~+~y^2}$
5. We know that, B is at a distance of 'a' from O. So the coordinates of B will be (a,0).
• Now we have three points and their coordinates:
B(a,0), F1(-c,0), F2(c,0)
• Using the distance formula, we can write some distances:
• First we write the distance BF1:
$\begin{array}{ll}
{}&{BF_1}
& {~=~}& {\sqrt{(a~-~ -c)^2~+~(0 - 0)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(a + c)^2}}
&{} \\
{}&{}
& {~=~}& {a + c}
&{} \\
\end{array}$
• Next we write the distance BF2:
$\begin{array}{ll}
{}&{BF_2}
& {~=~}& {\sqrt{(a~-~ c)^2~+~(0 - 0)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(a - c)^2}}
&{} \\
{}&{}
& {~=~}& {a - c}
&{} \\
\end{array}$
• Sum of the above two distances is: (a+c) + (a-c) = 2a
6. Both P and B are points on the same ellipse. So the sum of the distances must be equal.
Equating the results in (4) and (5), we get:
$\begin{array}{ll}
{}&{\sqrt{(x + c)^2~+~y^2}~+~\sqrt{(x - c)^2~+~y^2}}
& {~=~}& {2a}
&{} \\
{\Rightarrow}&{\sqrt{(x + c)^2~+~y^2}}
& {~=~}& {2a~-~\sqrt{(x - c)^2~+~y^2}}
&{} \\
{\Rightarrow}&{(x + c)^2~+~y^2}
& {~=~}& {4a^2~-~4a \sqrt{(x - c)^2~+~y^2}~+~(x - c)^2~+~y^2~~ \color {green} {\text{- - - (I)}}}
&{} \\
{\Rightarrow}&{x^2 + 2xc + c^2 + y^2}
& {~=~}& {4a^2~-~4a \sqrt{(x - c)^2~+~y^2}~+~x^2 - 2xc + c^2~+~y^2}
&{} \\
{\Rightarrow}&{2xc}
& {~=~}& {4a^2~-~4a \sqrt{(x - c)^2~+~y^2}- 2xc}
&{} \\
{\Rightarrow}&{4xc}
& {~=~}& {4a^2~-~4a \sqrt{(x - c)^2~+~y^2}}
&{} \\
{\Rightarrow}&{xc}
& {~=~}& {a^2~-~a \sqrt{(x - c)^2~+~y^2}~~ \color {green} {\text{- - - (II)}}}
&{} \\
{\Rightarrow}&{\frac{xc}{a}}
& {~=~}& {a~-~\sqrt{(x - c)^2~+~y^2}}
&{} \\
{\Rightarrow}&{\sqrt{(x - c)^2~+~y^2}}
& {~=~}& {a~-~\frac{xc}{a}~~ \color {green} {\text{- - - (III)}}}
&{} \\
{\Rightarrow}&{(x - c)^2~+~y^2}
& {~=~}& {a^2~-~\frac{2axc}{a}~+~\frac{x^2 c^2}{a^2}}
&{} \\
{\Rightarrow}&{(x - c)^2~+~y^2}
& {~=~}& {a^2~-~2cx~+~\frac{x^2 c^2}{a^2}}
&{} \\
{\Rightarrow}&{x^2 - 2cx + c^2~+~y^2}
& {~=~}& {a^2~-~2cx~+~\frac{x^2 c^2}{a^2}}
&{} \\
{\Rightarrow}&{x^2 + c^2~+~y^2}
& {~=~}& {a^2~+~\frac{x^2 c^2}{a^2}}
&{} \\
{\Rightarrow}&{x^2 ~+~y^2~-~\frac{x^2 c^2}{a^2}}
& {~=~}& {a^2 - c^2}
&{} \\
{\Rightarrow}&{x^2 \left(1~-~\frac{c^2}{a^2} \right)~+~y^2}
& {~=~}& {a^2 - c^2}
&{} \\
{\Rightarrow}&{x^2 \left(\frac{a^2~-~c^2}{a^2} \right)~+~y^2}
& {~=~}& {a^2 - c^2~~ \color {green} {\text{- - - (IV)}}}
&{} \\
{\Rightarrow}&{x^2 \left(\frac{b^2}{a^2} \right)~+~y^2}
& {~=~}& {b^2~~ \color {green} {\text{- - - (V)}}}
&{} \\
{\Rightarrow}&{\frac{x^2}{a^2}~+~\frac{y^2}{b^2}}
& {~=~}& {1}
&{} \\
\end{array}$
◼ Remarks:
• Line marked as (I):
In this line, we square both sides.
• Line marked as (II):
In this line, we divide both sides by 4.
• Line marked as (III):
In this line, we square both sides.
• Line marked as (IV):
In this line, write b2 in the place of a2 - c2.
• Line marked as (V):
In this line, we divide both sides by b2.
Using the above 6 steps, we derived an equation. Now we will prove the converse. It can be written in 9 steps:
1. We derived an equation: $\frac{x^2}{a^2}~+~\frac{y^2}{b^2}~=~1$
2. To prove the converse, we assume a point P.
• Let P(x,y) be any point on the ellipse.
• Distance of P from F1 can be written as:
$\begin{array}{ll}
{}&{PF_1}
& {~=~}& {\sqrt{(x~-~ -c)^2~+~(y - 0)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(x + c)^2~+~y^2}}
&{} \\
\end{array}$
3. But based on the equation written in (1), we can write:
$\begin{array}{ll}
{}&{\frac{y^2}{b^2}}
& {~=~}& {1-\frac{x^2}{a^2}}
&{} \\
{\Rightarrow}&{y^2}
& {~=~}& {b^2\left(1-\frac{x^2}{a^2} \right)}
&{} \\
\end{array}$
4. Substituting the above result in (2), we get:
$\begin{array}{ll}
{}&{PF_1}
& {~=~}& {\sqrt{(x + c)^2~+~y^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(x + c)^2~+~b^2\left(1-\frac{x^2}{a^2} \right)}}
&{} \\
{}&{}
&
{~=~}& {\sqrt{(x + c)^2~+~\left(a^2 - c^2 \right)
\left(1-\frac{x^2}{a^2} \right)}~~ \color {green} {\text{- - - (I)}}}
&{} \\
{}&{}
& {~=~}& {\sqrt{x^2 + 2cx + c^2~+~a^2 - x^2 - c^2 + \frac{c^2 x^2}{a^2}}}
&{} \\
{}&{}
& {~=~}& {\sqrt{2cx~+~a^2 + \frac{c^2 x^2}{a^2}}}
&{} \\
{}&{}
& {~=~}& {\sqrt{\left(a+\frac{cx}{a} \right)^2}}
&{} \\
{}&{}
& {~=~}& {a+\frac{cx}{a}}
&{} \\
\end{array}$
◼ Remarks:
• Line marked as (I):
In this line, we write a2 - c2 in the place of b2.
5. Now we consider the distance of P from F2. It can be written as:
$\begin{array}{ll}
{}&{PF_2}
& {~=~}& {\sqrt{(x~-~ c)^2~+~(y - 0)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(x - c)^2~+~y^2}}
&{} \\
\end{array}$
6. As we did in the case of PF1, here also, we substitute for y2. We get:
$\begin{array}{ll}
{}&{PF_2}
& {~=~}& {\sqrt{(x - c)^2~+~y^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(x - c)^2~+~b^2\left(1-\frac{x^2}{a^2} \right)}}
&{} \\
{}&{}
&
{~=~}& {\sqrt{(x - c)^2~+~\left(a^2 - c^2 \right)
\left(1-\frac{x^2}{a^2} \right)}~~ \color {green} {\text{- - - (I)}}}
&{} \\
{}&{}
& {~=~}& {\sqrt{x^2 - 2cx + c^2~+~a^2 - x^2 - c^2 + \frac{c^2 x^2}{a^2}}}
&{} \\
{}&{}
& {~=~}& {\sqrt{-2cx~+~a^2 + \frac{c^2 x^2}{a^2}}}
&{} \\
{}&{}
& {~=~}& {\sqrt{\left(a - \frac{cx}{a} \right)^2}}
&{} \\
{}&{}
& {~=~}& {a - \frac{cx}{a}}
&{} \\
\end{array}$
◼ Remarks:
• Line marked as (I):
In this line, we write a2 - c2 in the place of b2.
7. So the sum of the distances of P from F1 and F2 is:
(PF1 + PF2) = (a + xc/a) + (a - xc/a) = 2a.
8. Consider step (5) below fig.11.34 at the beginning of this section. We saw that, sum of the distances of point B from the foci is '2a'.
9. So any point P(x,y) on the ellipse will satisfy the equation $\frac{x^2}{a^2}~+~\frac{y^2}{b^2}~=~1$
• The converse is proved.
◼ So we can write:
If the center of the ellipse is at O, major axis lies along the x-axis and minor axis lies along the y-axis, then equation of the ellipse is: $\frac{x^2}{a^2}~+~\frac{y^2}{b^2}~=~1$
Based on the above equation of the ellipse, we can write two interesting facts:
Fact 1:
This can be written in 5 steps:
1. We have: $\frac{x^2}{a^2}~+~\frac{y^2}{b^2}~=~1$
2. This can be rearranged as: $\frac{x^2}{a^2}~=~1~-~\frac{y^2}{b^2}$
• So $\frac{x^2}{a^2}$ will be always less than 1.
• That is: $\frac{x^2}{a^2}~\le~1$
⇒ $x^2 ~\le~a^2$
3. Solving the above inequality, we get:
♦ x should not be less than -a.
♦ x should not be greater than a.
• That is: $-a~\le~x~\le~a$
4. So we can write:
• Consider any point on the ellipse.
♦ The x-coordinate of that point will be greater than -a.
♦ The x-coordinate of that point will be less than a.
5. So the ellipse will lie between two vertical lines.
♦ The left vertical line is x = -a.
♦ The right vertical line is x = a.
Fact 2:
This can be written in 5 steps:
1. We have: $\frac{x^2}{a^2}~+~\frac{y^2}{b^2}~=~1$
2. This can be rearranged as: $\frac{y^2}{b^2}~=~1~-~\frac{x^2}{a^2}$
• So $\frac{y^2}{b^2}$ will be always less than 1.
• That is: $\frac{y^2}{b^2}~\le~1$
⇒ $y^2 ~\le~b^2$
3. Solving the above inequality, we get:
♦ y should not be less than -b.
♦ y should not be greater than b.
• That is: $-b~\le~y~\le~a$
4. So we can write:
• Consider any point on the ellipse.
♦ The y-coordinate of that point will be greater than -b.
♦ The y-coordinate of that point will be less than b.
5. So the ellipse will lie between two horizontal lines.
♦ The upper horizontal line is y = b.
♦ The lower horizontal line is y = -b.
• The ellipse and the lines in fig.11.35 below, demonstrates the two facts:
 |
| Fig.11.35 |
• Equation of the ellipse in the above fig. is: $\frac{x^2}{5^2}~+~\frac{y^2}{3^2}~=~1$
• We see that:
♦ Value of 'a' is 5.
✰ The vertical lines are related to 5.
♦ Value of 'b' is 3.
✰ The horizontal lines are related to 3.
• In this section, we saw a simplest equation of an ellipse.
♦ The major axis lies along the x-axis.
♦ The minor axis lies along the y-axis.
• We will get another simplest equation also when:
♦ The major axis lies along the y-axis.
♦ The minor axis lies along the x-axis.
• We will see it in the next section.