20.12 - Adjoint And Inverse of A Matrix

In the previous section, we saw Minors and Cofactors. In this section, we will see adjoint and inverse of a matrix.

Adjoint of a Matrix

Some basics can be written in 6 steps:
1. Consider a square matrix A = [a_ij]_n.
2. We know how to write the Cofactor A_ij of any element a_ij of the matrix A.
3. So we can write a new matrix which contains the Cofactors.
• For example, if the original matrix is
$A ~=~\left [\begin{array}{r}                           
a_{11}      &{    a_{12}    } &{    a_{13}    }    \\
a_{21}      &{    a_{22}    } &{    a_{23}    }    \\
a_{31}      &{    a_{32}    } &{    a_{33}    }    \\
\end{array}\right ]$,
then the corresponding matrix of Cofactors will be:
$\left [\begin{array}{r}                           
A_{11}      &{    A_{12}    } &{    A_{13}    }    \\
A_{21}      &{    A_{22}    } &{    A_{23}    }    \\
A_{31}      &{    A_{32}    } &{    A_{33}    }    \\
\end{array}\right ]$

4. Now, the transpose of the matrix of Cofactors will be:
$\left [\begin{array}{r}                           
A_{11}      &{    A_{21}    } &{    A_{31}    }    \\
A_{12}      &{    A_{22}    } &{    A_{32}    }    \\
A_{13}      &{    A_{23}    } &{    A_{33}    }    \\
\end{array}\right ]$
• This matrix obtained by transposing, is called adjoint matrix.
5. Adjoint of matrix A is denoted by adj A.
6. For the example matrix A mentioned in (3),
adj A = $\left [\begin{array}{r}                           
A_{11}      &{    A_{21}    } &{    A_{31}    }    \\
A_{12}      &{    A_{22}    } &{    A_{32}    }    \\
A_{13}      &{    A_{23}    } &{    A_{33}    }    \\
\end{array}\right ]$

Solved example 20.19
Find adj A for $A~=~\left [\begin{array}{r}   
2       &{    5    }    \\
-3       &{    7    }    \\
\end{array}\right ]$
Solution:
1. First we will find the Minors and Cofactors:

2. So the matrix of Cofactors is:
$\left [\begin{array}{r}   
7       &{    3    }    \\
-5       &{    2    }    \\
\end{array}\right ]$

3. The transpose of the above matrix, is the required adjoint matrix. So we get:

$\text{adj A}~=~\left [\begin{array}{r}   
7       &{    -5    }    \\
3       &{    2    }    \\
\end{array}\right ]$

---

For any square matrix of order 2, there is a direct method to find the adjoint. It can be written in 4 steps:
1. Fig.20.5(a) below shows the original matrix A.

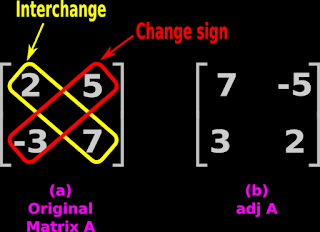Fig.20.5

2. Consider the yellow diagonal, which is drawn from left-top to right-bottom. We need to interchange the elements in this diagonal.   
3. Consider the red diagonal, which is drawn from right-top to left-bottom. We should not interchange the elements in this diagonal. But we must change the signs of those elements.
4. The resulting new matrix is the adj A. It is shown in fig.20.5(b) above.

---

Now we will see four theorems related to adjoint matrices.

Theorem I
• If A is any given square matrix of order n, then
A(adj A) = (adj A)A = |A|I
    ♦ Where I is the identity matrix of the same order n.

Verification can be written in steps:
1. Let $A ~=~\left [\begin{array}{r}                           
a_{11}      &{    a_{12}    } &{    a_{13}    }    \\
a_{21}      &{    a_{22}    } &{    a_{23}    }    \\
a_{31}      &{    a_{32}    } &{    a_{33}    }    \\
\end{array}\right ]$.
• Then adj A will be: $\left [\begin{array}{r}       
A_{11}      &{    A_{21}    } &{    A_{31}    }    \\
A_{12}      &{    A_{22}    } &{    A_{32}    }    \\
A_{13}      &{    A_{23}    } &{    A_{33}    }    \\
\end{array}\right ]$
2. We know how to write the product A(adj A).
• Let us write the first element (intersection of R₁ and C₁):
a₁₁ A₁₁ + a₁₂ A₁₂ + a₁₃ A₁₃
• We see that:
    ♦ First term is the product of a₁₁ and it’s Cofactor.
    ♦ Second term is the product of a₁₂ and it’s Cofactor.
    ♦ Third term is the product of a₁₃ and it’s Cofactor.            
    ♦ Also, we are taking the sum of the three terms.
3. So we can write:
The first element in A(adj a) is: The determinant |A|
4. All diagonal elements of A(adj a), will be similar to the form written in (2).
• So all diagonal elements in A(adj a), will become |A|
5. Let us write the second element (intersection of R₁ and C₂) of A(adj a):
a₁₁ A₂₁ + a₁₂ A₂₂ + a₁₃ A₂₃
• We see that:
    ♦ First term is the product of a₁₁ and a different Cofactor.
    ♦ Second term is the product of a₁₂ and a different Cofactor.
    ♦ Third term is the product of a₁₃ and a different Cofactor.
    ♦ Also, we are taking the sum of the three terms.
6. So we can write:
The second element in A(adj a) is: zero
7. All non-diagonal elements of A(adj a), will be similar to the form written in (5).
• So all non-diagonal elements in A(adj a), will become zero.
8. Thus we get:
$A(\text{adj A})~=~\left[\begin{array}{r}   
|A|    &{    0    }    &{    0    }    \\
0    &{    |A|    }    &{    0    }    \\
0    &{    0    }    &{    |A|    }    \\
\end{array}\right]
~=~|A|\left[\begin{array}{r}                           
1    &{    0    }    &{    0    }    \\
0    &{    1    }    &{    0    }    \\
0    &{    0    }    &{    1    }    \\
\end{array}\right]~=~|A|I$
9. Similarly, we can show that (adj A)A = |A|I
10. Based on (8) and (9), we can write:
A(adj A) = (adj A) A = |A|I

Theorem II
If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.
(We will see the proof of this theorem in higher classes)
    ♦ A square matrix A is said to be singular if |A| = 0
    ♦ A square matrix A is said to be non-singular if |A| ≠ 0

Theorem III
If A and B are square matrices of the same order, then |AB| = |A| |B|.
(We will see the proof of this theorem in higher classes)

---

Now we can write about an interesting result. It can be written in 4 steps:

1. Let A be a square matrix of order 3.
2. Let us try to simplify (adj A)A: 

◼ Remarks:
• 1 (magenta color): Here we use theorem I
• 2 (magenta color): In the R.H.S, the unit matrix is multiplied by a constant value. So all non-diagonal elements of the resulting matrix will be zeroes.
• 3 (magenta color): Here we take determinants on both sides.
• 5 (magenta color): Here we apply theorem III in the L.H.S.

3. We see that:
• We started the calculations with a square matrix A of order 3.
• In the final result, the determinant of A has a power of 2.
4. So we can write the general form:
If A is a square matrix of order n, then
|(adj a)| = |A|^n-1.
(We will see the actual proof in higher classes)

---

Theorem IV
A square matrix A is invertible if and only if A is a non-singular matrix.
• Proof can be written in 3 steps:
1. Let A be a invertible matrix of order n. Also, let I be an identity matrix of the same order n.
• Then, from the discussion that we had on matrices in the previous chapter, we can write: AB = BA = I.
    ♦ Where B is a square matrix of order n.
2. Consider the equation AB = I
• Writing determinants of matrices on both sides, we get:
|AB| = |I|
• This is same as |AB| = 1
3. Applying theorem III on the L.H.S, we get: |A| |B| = 1.
• |A| and |B| are numbers. If their product is 1, it means that, none of them can be zero.
• So we get: |A| ≠ 0.
• That means, A is a non-singular matrix.

Converse of Theorem IV
If A is a non-singular square matrix, then it is invertible.
• Proof can be written in 3 steps:
1. Consider theorem I:
A(adj A) = (adj A) A = |A|I
2. |A| is a number. So we can use it to divide the whole equation. We get:
$A \left(\frac{1}{|A|}(\text{adj A}) \right)~=~ \left(\frac{1}{|A|}(\text{adj A}) \right)A~=~I$
3. We can rearrange this equation into a familiar form, if we put 'B' in the place of $\frac{1}{|A|}(\text{adj A})$.
• We get: AB = BA = I
4. The above result implies that, matrix B is the inverse of matrix A.
• So we can write:
A is invertible and the inverse is $\frac{1}{|A|}(\text{adj A})$

---

In the next section, we will see some solved examples.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com