In the previous section,
we saw collinearity of three points.
In this section, we will see the various forms of the equation of a line.
Some basics can be written in 3 steps:
1. Consider a line L lying in the xy-plane.
•
We know that in any line, there will be infinite number of points.
•
But there are other infinite points which do not lie on the line.
2. Then what is the difference between the following two types of points:
(i) Points which lie on L
(ii) Points which do not lie on L
•
The answer is:
♦ All points lying on L, will satisfy a particular condition.
♦ The points which do not lie on L, will not satisfy that condition.
3. We can write this is another way also:
Take any point on the xy-plane. If that point satisfies a particular condition, then that point will lie on L.
• So our next aim is to find the conditions for different types of lines.
•
First we will see horizontal lines.
Equation of a horizontal line
This can be written in 9 steps.
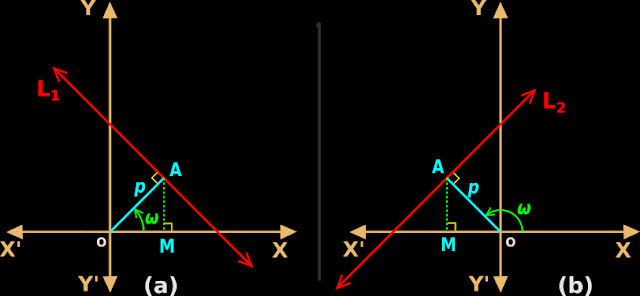
1. The red line L1 in fig.10.16(a) is parallel to the x-axis.
♦ It is a horizontal line.
♦ It is at a distance of ‘a’ from the x-axis.
 |
| Fig.10.16 |
2. Consider any point on L
1. The ordinate (y-coordinate) of that point will be 'a'.
•
Conversely, any point whose ordinate is a, will lie on L
13. So we can write:
The condition for a point to lie on L
1 is that, the ordinate of that point must be ‘a’
4. In algebraic form, we can write: y = a
•
This algebraic form is the equation of line L
1•
We can write:
Equation of L
1 is:
y = a5. Now consider the red line L
1' in fig.10.16(b) above.
♦ It is parallel to the x-axis
♦ It is a horizontal line.
♦ It is at a distance of ‘a’ from the x-axis.
6. Consider any point on L
1'. The ordinate (y-coordinate) of that point will be '-a'.
•
Conversely, any point whose ordinate is -a, will lie on L
1'
7. So we can write:
The condition for a point to lie on L
1' is that, the ordinate of that point must be ‘-a’
8. In algebraic form, we can write: y = -a
•
This algebraic form is the equation of line L
1'
•
We can write:
Equation of L
1' is:
y = -a9. In general, we can write:
Equation of any horizontal line will be in the form: $y=\pm a$
♦ Where ‘a’ is a constant.
✰ We use the ‘+’ sign when the horizontal line is above the x-axis.
✰ We use the ‘-’ sign when the horizontal line is below the x-axis.
Equation of a vertical line
This can be written in 9 steps.
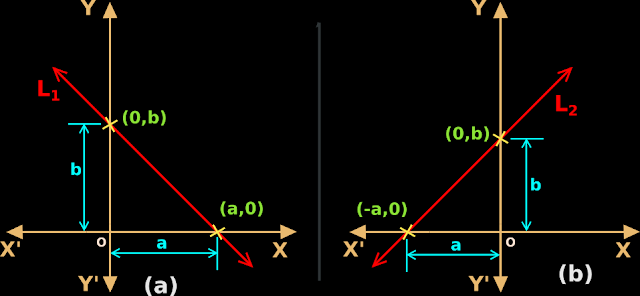
1. The red line L2 in fig.10.17(a) is parallel to the y-axis.
♦ It is a vertical line.
♦ It is at a distance of ‘b’ from the y-axis.
 |
| Fig.10.17 |
2. Consider any point on L
2. The abscissa (x-coordinate) of that point will be 'b'.
•
Conversely, any point whose abscissa is 'b', will lie on L
23. So we can write:
The condition for a point to lie on L
2 is that, the abscissa of that point must be ‘b’
4. In algebraic form, we can write: x = b
•
This algebraic form is the equation of line L
2•
We can write:
Equation of L
2 is:
x = b5. Now consider the red line L
2' in fig.10.17(b) above.
♦ It is parallel to the y-axis
♦ It is a vertical line.
♦ It is at a distance of ‘b’ from the y-axis.
6. Consider any point on L
2'. The abscissa (x-coordinate) of that point will be '-b'.
•
Conversely, any point whose abscissa is -b, will lie on L
2'
7. So we can write:
The condition for a point to lie on L
2' is that, the abscissa of that point must be ‘-b’
8. In algebraic form, we can write: x = -b
•
This algebraic form is the equation of line L
2'
•
We can write:
Equation of L
2' is:
x = -b9. In general, we can write:
Equation of any vertical line will be in the form: $x=\pm b$
♦ Where ‘b’ is a constant.
✰ We use the ‘+’ sign when the vertical line is on the right side of the y-axis.
✰ We use the ‘-’ sign when the vertical line is on the left side of the y-axis.
Solved Example 10.8
Write the equation of the line parallel to x-axis and passing through (-2,3). Also write the equation of the line parallel to y-axis and passing through the same point.
Solution:
1. First we will consider the line parallel to the x-axis.
•
It's equation will be of the form $y = \pm a$
•
This line passes through (-2,3). So it's distance from the x-axis is 3 units.
♦ That means, a = 3
•
Also, (-2,3) is above the x-axis.
♦ So we use the +ve sign
•
So the required equation is: $y = 3$
2. Next we will consider the line parallel to the y-axis.
•
It's equation will be of the form $x = \pm b$
•
This line passes through (-2,3). So it's distance from the y-axis is 2 units.
♦ That means, a = 2
•
Also, (-2,3) is on the left side of the y-axis.
♦ So we use the -ve sign
•
So the required equation is: $x = -2$
3. The actual lines are shown in the fig.10.18 below:
 |
| Fig.10.18 |
•
In the above fig,
♦ The red line is the required line parallel to the x-axis.
♦ The green line is the required line parallel to the y-axis.
Point-slope form
•
Suppose that, we are given the following two items:
♦ Slope of a line.
♦ A point through which the line passes.
•
Then we can quickly write the equation of that line. Let us see how it is done. It can be written in 7 steps:
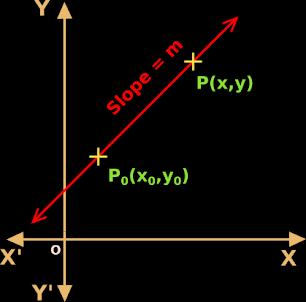
1. Let the slope of the line be m
2. Let the line pass through a known point P0 (x0,y0)
•
By saying "Known point", we mean that, the values of x0 and y0 are known.
3. Let P(x,y) be any point on the line.
4. Now we have two points on the line. They are: P0(x0,y0) and P(x,y). This is shown in fig.10.19 below:
 |
| Fig.10.19 |
5. If we have two points on a line, we can write the slope of the line.
•
So in our present case, the slope will be $\frac{y-y_0}{x-x_0}$
6. But we are already given the slope. It is m. So we can write:
$\begin{array}{ll}
{}&{m}
&{}={}& {\frac{y-y_0}{x-x_0}}
&{} \\
{\Rightarrow}&{y-y_0}
&{}={}& {m(x-x_0)}
&{} \\
\end{array}$
7. So we get an equation: y-y0 = m(x-x0)
•
We derived this equation by assuming that, the point (x,y) lies on the line (see fig.10.19).
•
That means,
♦ if we take any point outside the line, this equation will not be satisfied.
♦ if we take any point on the line, this equation will be satisfied.
•
So we can say that, y-y0 = m(x-x0) is the equation of the line.
♦ This is the equation of a line written in slope-point form.
✰ The slope is m.
✰ The point is (x0,y0).
Let us see a solved example:
Solved example 10.9
Three lines L1, L2 and L3 pass through the point (-3,4). Write the equation of each of those lines, if their slopes are -3, 2 and 4 respectively.
Solution:
•
Given that,
♦ (x0,y0) = (-3,4)
♦ m1 = -3
♦ m2 = 2
♦ m3 = 4
•
We have the slope-point form: y-y0 = m(x-x0)
1. So for L1, the equation will be:
$\begin{array}{ll}
{}&{y-4}
&{}={}& {-3(x-~-3)}
&{} \\
{\Rightarrow}&{y-4}
&{}={}& {-3x-9}
&{} \\
{\Rightarrow}&{3x + y +5}
&{}={}& {0}
&{} \\
\end{array}$
2. Similarly for L2, the equation will be:
$\begin{array}{ll}
{}&{y-4}
&{}={}& {2(x-~-3)}
&{} \\
{\Rightarrow}&{y-4}
&{}={}& {2x+6}
&{} \\
{\Rightarrow}&{2x - y +10}
&{}={}& {0}
&{} \\
\end{array}$
3. Finally for L3, the equation will be:
$\begin{array}{ll}
{}&{y-4}
&{}={}& {4(x-~-3)}
&{} \\
{\Rightarrow}&{y-4}
&{}={}& {4x+12}
&{} \\
{\Rightarrow}&{4x - y +16}
&{}={}& {0}
&{} \\
\end{array}$
4. The actual plot of the three lines are shown in fig.10.20 below:
 |
| Fig.10.20 |
5. We can infer some general information from the plot. They can be written in 3 steps:
(i) If the slope of a line is +ve, that line will have an upward slope. That means, when we move along the x-axis towards the +ve side, the line will be sloping upwards.
♦ Lines L2 and L3 are examples.
(ii) If the slope of a line is -ve, that line will have a downward slope.
That means, when we move along the x-axis towards the +ve side, the
line will be sloping downwards.
♦ Line L1 is an example.
(iii) Compare the slopes of two lines.
♦ The line with the greater slope will be steeper.
♦ The line with the lesser slope will be flatter.
•
This will become clear when we compare L2 and L3.
Two-point form
•
Suppose that, we are given two known points on a line.
•
Then we can quickly write the equation of that line. Let us see how it is done. It can be written in 6 steps:
1. Let the line pass through two known points P1 (x1,y1) and P2 (x2,y2)
•
By saying "Known points", we mean that, the values of x1, y1, x2 and y2 are known.
2. Let P(x,y) be any point on the line.
3. Now we have three points on the line. They are: P1(x1,y1), P2(x2,y2) and P(x,y). This is shown in fig.10.21 below:
 |
| Fig.10.21 |
4. If there are three points, we can write slopes.
•
So in our present case,
♦ the slope of line P1P will be $\frac{y-y_1}{x-x_1}$
♦ the slope of line P1P2 will be $\frac{y_2-y_1}{x_2-x_1}$
5. But since the three points are collinear, the slopes will be equal. So we can write:
$\begin{array}{ll}
{}&{\frac{y-y_1}{x-x_1}}
&{}={}& {\frac{y_2-y_1}{x_2-x_1}}
&{} \\
{\Rightarrow}&{y-y_1}
&{}={}& {\frac{y_2-y_1}{x_2-x_1} (x-x_0)}
&{} \\
\end{array}$
6. So we get an equation: $y-y_1~=~\frac{y_2-y_1}{x_2-x_1} (x-x_1)$
•
We derived this equation by assuming that, the point (x,y) lies on the line (see fig.10.21).
•
That means,
♦ if we take any point outside the line, this equation will not be satisfied.
♦ if we take any point on the line, this equation will be satisfied.
•
So we can say that, $y-y_1~=~\frac{y_2-y_1}{x_2-x_1} (x-x_1)$ is the equation of the line.
♦ This is the equation of a line written in two-point form.
✰ The two points are: (x1,y1) and (x2,y2).
Let us see a solved example:
Solved example 10.10
Write the equations of the following lines:
(i) Line L1, passing through (-1, -3) and (2, 4).
(ii) Line L2, passing through (-3, 7) and (6, 7).
Solution:
Part (i):
•
We have the two-point form: $y-y_1~=~\frac{y_2-y_1}{x_2-x_1} (x-x_1)$
•
Substituting the known values, we get:
$\begin{array}{ll}
{}&{y-~-3}
&{}={}& {\frac{4-~-3}{2-~-1} (x-~-1)}
&{} \\
{\Rightarrow}&{y+3}
&{}={}& {\frac{7}{3} (x+1)}
&{} \\
{\Rightarrow}&{3y+9}
&{}={}& {7x+7}
&{} \\
{\Rightarrow}&{7x-3y-2}
&{}={}& {0}
&{} \\
\end{array}$
Part (ii):
•
We have the two-point form: $y-y_1~=~\frac{y_2-y_1}{x_2-x_1} (x-x_1)$
•
Substituting the known values, we get:
$\begin{array}{ll}
{}&{y-7}
&{}={}& {\frac{7-7}{6-~-3} (x-~-3)}
&{} \\
{\Rightarrow}&{y-7}
&{}={}& {\frac{0}{9} (x+3)}
&{} \\
{\Rightarrow}&{y-7}
&{}={}& {0}
&{} \\
{\Rightarrow}&{y}
&{}={}& {7}
&{} \\
\end{array}$
•
The actual plots are shown in fig.10.22 below:
 |
| Fig.10.22 |
•
Note:
In the case of L
2, we see that, it is horizontal. Indeed we obtained the slope $\frac{y_2 - y_1}{x_2 - x_1}$ = 0 for L
2
Slope-intercept form
•
Let us first see, what intercept is. It can be written in 6 steps:
1. In fig.10.23(a) below, the line L1 intersects the x-axis at (a,0)
•
The distance of the ‘point of intersection’ from the origin O is ‘a’.
•
We say that, the x-intercept of the line is +a.
 |
| Fig.10.23 |
2. In fig.10.23(b) above, the line L
2 intersects the x-axis at (-b,0)
•
The distance of the ‘point of intersection’ from the origin O is ‘b’
•
We say that, the x-intercept of the line is -b.
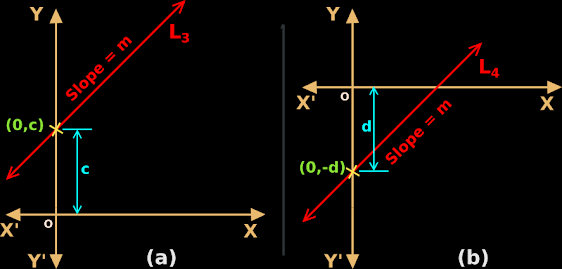
3. In fig.10.24(a) below, the line L
3 intersects the y-axis at (c,0)
•
The distance of the ‘point of intersection’ from the origin O is ‘c’.
•
We say that, the y-intercept of the line is +c.
 |
| Fig.10.,24 |
4. In fig.10.24(b) above, the line L4 intersects the x-axis at (-d,0)
•
The distance of the ‘point of intersection’ from the origin O is ‘d’
•
We say that, the x-intercept of the line is -d.
5. So intercept is the distance of the point of intersection from O with the proper sign.
6. While writing intercepts, it is better to remember that:
•
Any non-parallel line will intersect the x-axis.
♦ In some cases, the point of intersection will be on the right side of y-axis.
✰ Then the point of intersection will be of the type (a,0)
♦ In the remaining cases, the point of intersection will be on the left side of y-axis.
✰ Then the point of intersection will be of the type (-b,0)
•
Any non-parallel line will intersect the y-axis.
♦ In some cases, the point of intersection will be above the x-axis.
✰ Then the point of intersection will be of the type (0,c)
♦ In the remaining cases, the point of intersection will be below the x-axis.
✰ Then the point of intersection will be of the type (0,-d)
•
Suppose that, we are given the following two items:
♦ Slope of a line.
♦ x-intercept or y-intercept of the line.
•
Then we can quickly write the equation of that line. Let us see how it is done.
Case I: The x-intercept is +ve.
This can be written in 4 steps:
1. Let the slope of the line be m
2. Let the x-intercept be +a
•
Then we can say that, the line passes through (a,0). See fig.10.23(a) above.
3. Now we have two items:
♦ Slope of the line.
♦ A point through which the line passes.
4. So we can use the point-slope form: y-y0 = m(x-x0)
•
Here, x0 is 'a' and y0 is 0
•
Thus the equation becomes:
$\begin{array}{ll}
{}&{y-0}
&{}={}& {m(x-a)}
&{} \\
{\Rightarrow}&{y}
&{}={}& {m(x-a)}
&{} \\
\end{array}$
Case II: The x-intercept is -ve.
This can be written in 4 steps:
1. Let the slope of the line be m
2. Let the x-intercept be -b
•
Then we can say that, the line passes through (-b,0). See fig.10.23(b) above.
3. Now we have two items:
♦ Slope of the line.
♦ A point through which the line passes.
4. So we can use the point-slope form: y-y0 = m(x-x0)
•
Here, x0 is '-b' and y0 is 0
•
Thus the equation becomes:
$\begin{array}{ll}
{}&{y-0}
&{}={}& {m(x- -b)}
&{} \\
{\Rightarrow}&{y}
&{}={}& {m(x+b)}
&{} \\
\end{array}$
• Based on cases I and II, we can write:
When the slope and x-intercept is given, we can use the general form: y = m(x-a)
♦ When the intercept is +ve, we give a +ve value for 'a'.
♦ When the intercept is -ve, we give a -ve value for 'a'.
Case III: The y-intercept is +ve.
This can be written in 4 steps:
1. Let the slope of the line be m
2. Let the y-intercept be +c
•
Then we can say that, the line passes through (0,c). See fig.10.24(a) above.
3. Now we have two items:
♦ Slope of the line.
♦ A point through which the line passes.
4. So we can use the point-slope form: y-y0 = m(x-x0)
•
Here, x0 is 0 and y0 is 'c'
•
Thus the equation becomes:
$\begin{array}{ll}
{}&{y-c}
&{}={}& {m(x-0)}
&{} \\
{\Rightarrow}&{y-c}
&{}={}& {mx}
&{} \\
{\Rightarrow}&{y}
&{}={}& {mx + c}
&{} \\
\end{array}$
Case IV: The y-intercept is -ve.
This can be written in 4 steps:
1. Let the slope of the line be m
2. Let the y-intercept be -d
•
Then we can say that, the line passes through (0,-d). See fig.10.24(b) above.
3. Now we have two items:
♦ Slope of the line.
♦ A point through which the line passes.
4. So we can use the point-slope form: y-y0 = m(x-x0)
•
Here, x0 is 0 and y0 is '-d'
•
Thus the equation becomes:
$\begin{array}{ll}
{}&{y-~-d}
&{}={}& {m(x-0)}
&{} \\
{\Rightarrow}&{y+d}
&{}={}& {mx}
&{} \\
{\Rightarrow}&{y}
&{}={}& {mx - d}
&{} \\
\end{array}$
• Based on cases III and IV, we can write:
When the slope and y-intercept is given, we can use the general form: y = mx+c
♦ When the intercept is +ve, we give a +ve value for 'c'.
♦ When the intercept is -ve, we give a -ve value for 'c'.
Let us see a solved example:
Solved example 10.11
Write the equations of the following lines:
(i) Line L1 for which tan 𝜃 = 1/3 and x-intercept is 4.
(ii) Line L2 for which tan 𝜃 = 1/2 and y-intercept is -(11/2).
𝜃 is the inclination of the line.
Solution:
Part (i):
• 𝜃 is the inclination of the line. So tan 𝜃 will be the slope.
♦ So we can write: m = 1/3
•
x-intercept is 4.
♦ We use the general equation: y = m(x-a)
♦ Here 'a' is 4.
•
Substituting the known values, we get:
$\begin{array}{ll}
{}&{y}
&{}={}& {\frac{1}{3} (x-4)}
&{} \\
{\Rightarrow}&{3y}
&{}={}& {x-4}
&{} \\
{\Rightarrow}&{x-3y-4}
&{}={}& {0}
&{} \\
\end{array}$
Part (ii):
• 𝜃 is the inclination of the line. So tan 𝜃 will be the slope.
♦ So we can write: m = 1/2
•
y-intercept is -(11/2).
♦ We use the general equation: y = mx + c
♦ Here 'c' is -(11/2)
•
Substituting the known values, we get:
$\begin{array}{ll}
{}&{y}
&{}={}& {\frac{1 x}{2} - \frac{11}{2}}
&{} \\
{\Rightarrow}&{2y}
&{}={}& {x-11}
&{} \\
{\Rightarrow}&{x-2y-11}
&{}={}& {0}
&{} \\
\end{array}$
•
The actual plots are shown in fig.10.25 below:
 |
| Fig.10.25 |
•
We can see that:
♦ L1 intersects the x-axis at (4,0)
♦ L2 intersects the x-axis at (0,-11/2)
In the next section, we will see intercept form and normal form.
Previous
Contents
Next
Copyright©2022 Higher secondary mathematics.blogspot.com