In the previous section, we completed a discussion on sequences and series. In this chapter, we will see Straight lines.
In our earlier classes, we have discussed problems related to coordinate geometry. Let us recall some of those topics:
A. Significance of coordinates
This can be written in 3 steps:
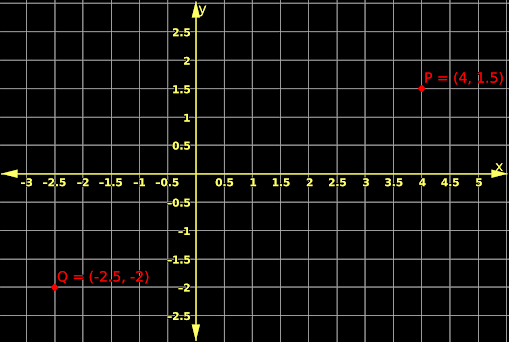
1. In fig.10.1 below, points P and Q lie on the XY plane.
 |
| Fig.10.1 |
2. The coordinates of the point P are (4,1.5)
• Then we can write:
♦ P is at a distance of 4 units from the y-axis.
✰ This distance is measured along the +ve x-axis.
♦ P is at a distance of 1.5 units from the x-axis.
✰ This distance is measured along the +ve y-axis.
3. The coordinates of the point Q are (-2.5,-2)
• Then we can write:
♦ Q is at a distance of 2.5 units from the y-axis.
✰ This distance is measured along the -ve x-axis.
♦ Q is at a distance of 2 units from the x-axis.
✰ This distance is measured along the -ve y-axis
B. Distance between two points
This can be written in 3 steps:
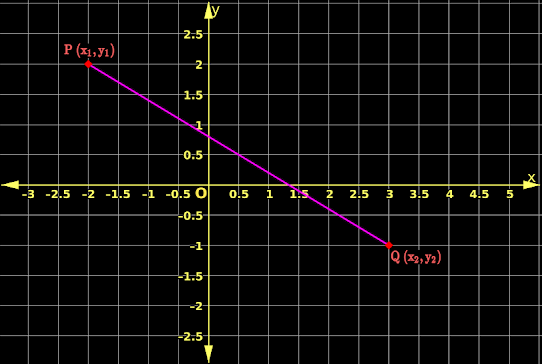
1. In fig.10.2 below, points P (x1,y1) and Q (x2,y2) lie on the XY-plane.
 |
| Fig.10.2 |
2. Then the distance between the two points can be obtained using the formula:
$\rm{PQ~=~\sqrt{\left(x_2 - x_1 \right)^2~+~\left(y_2 - y_1 \right)^2}}$
3. For example, if (x1,y1) is (-2,2) and (x2,y2) is (3,-1), then:
$\begin{array}{ll}
{PQ}&{}={}
&{\sqrt{\left(3 - (-2) \right)^2~+~\left(-1 - 2 \right)^2}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\sqrt{\left(5 \right)^2~+~\left(-3 \right)^2}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\sqrt{25~+~9}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\sqrt{34}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{5.83~\text{units}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
\end{array}$
◼ We have seen this topic in our earlier classes (Details here)
C. Division of a line in the ratio m:n
This can be written in 4 steps:
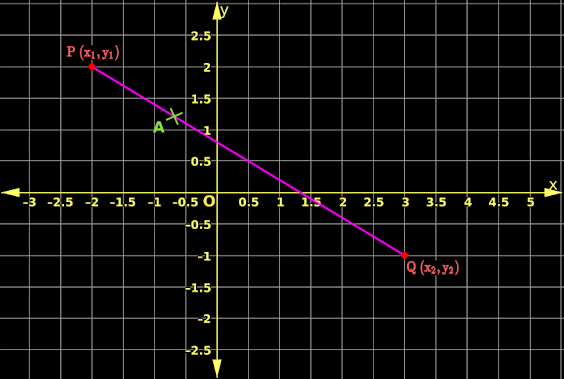
1. In fig.10.3 below, PQ is a line with end points P (x1,y1) and Q (x2,y2)
 |
| Fig.10.3 |
2. Point A divides the line in the ratio m:n
That is:
$\text{Distance PA = Distance PQ}~ × ~\frac{m}{m+n}$
$\text{Distance QA = Distance PQ}~ × ~\frac{n}{m+n}$
3. Then the coordinates of A are:
$\frac{m\, x_2 ~+~n\, x_1}{m+n},~\frac{m\, y_2 ~+~n\, y_1}{m+n}$
◼ Note:
• For this formula to be valid,
♦ The "segment represented by the first component m", must be adjacent to the first point (x1, y1).
4. For example, let:
♦ P (x1,y1) be P (-2,2)
♦ Q (x2,y2) be Q (3,-1)
♦ Point A divides PQ in the ratio 3:10
• Then:
$\begin{array}{ll}
{\text{Coordinates of A}}&{}={}
&{\left(\frac{3 × 3~+~10 × -2}{3+10}\right.~,}& {\left. \frac{3 × -1~+~10 × 2}{3+10} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\left(\frac{9~-~20}{13}\right.~,}& {\left. \frac{-3~+~20}{13} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\left(\frac{-11}{13}\right.~,}& {\left. \frac{17}{13} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\left(-0.85 \right.~,}& {\left. 1.3 \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
\end{array}$
• In this example, the ratio m:n is 3:10. The first component of the ratio is 3. The "segment represented by the first component 3", is adjacent to the first point P (-2,2).
◼ We have seen this topic in our earlier classes (Details here)
D. Division of a line in the ratio m:m
This can be written in 3 steps:
1. In this case, the point A divides the line PQ into two equal segments (remember that, m:m is same as 1:1).
• That means, A is the midpoint of PQ
2. We can write:
$\begin{array}{ll}
{\text{Coordinates of A}}&{}={}
&{\left(\frac{m\, x_2 ~+~n\, x_1}{m+n}\right.~,}& {\left. \frac{m\, y_2 ~+~n\, y_1}{m+n} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\left(\frac{m\, x_2 ~+~m\, x_1}{m+m}\right.~,}& {\left. \frac{m\, y_2 ~+~m\, y_1}{m+m} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\left(\frac{m(x_2 ~+~x_1)}{2m}\right.~,}& {\left. \frac{m(y_2 ~+~y_1}{2m} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\left(\frac{x_1 ~+~x_2}{2}\right.~,}& {\left. \frac{y_1 ~+~y_2}{2} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
\end{array}$
3. This result can be used as a formula:
Coordinates of the midpoint of the line PQ with P (x1,y1) and Q (x2,y2) are:
$\left(\frac{x_1~+~x_2}{2},\frac{y_1~+~y_2}{2} \right)$
E. Area of a Triangle
This can be written in 4 steps:
1. In fig.10.4 below, PQR is a triangle with vertices P (x1,y1), Q (x2,y2) and R (x3,y3)
 |
| Fig.10.4 |
2. Area of the triangle PQR will be equal to:
$\frac{1}{2}\left|x_1(y_2 - y_3)~+~x_2(y_3 - y_1)~+~x_3(y_1 - y_2) \right|$
• The calculations may give a -ve result. But we can ignore the -ve sign. This is indicated by the || lines.
3. Let us see an example:
If the vertices of a triangle are P (-1,5,2), Q (-2.5,-2) and R (4,1.5), then the area of that triangle will be:
$\begin{array}{ll}
{\text{Area}}&{}={}
&{\frac{1}{2}~ × ~\left |-1.5(-2 - 1.5)~+~-2.5(1.5 - 2)~+~4(2 - -2)\right |}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\frac{1}{2}~ × ~\left |-1.5(- 3.5)~+~-2.5(-0.5)~+~4(4)\right |}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\frac{1}{2}~ × ~\left |5.25~+~1.25~+~16\right |}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{\frac{1}{2}~ × ~\left |22.5\right |}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
{}&{}={}
&{11.25~\text{square units}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
\end{array}$
4. Suppose that we are given three points P, Q and R.
• Using their coordinates, we find the area formed by the three points.
• If that area works out to zero, we can confirm that, P, Q and R lie on a line.
♦ In other words, P, Q and R are collinear.
• We can draw geometric figures like triangles, rectangles, parallelograms etc., on the XY-plane. All we need is the "coordinates of the vertices" of those geometric figures.
• So it is clear that, coordinate geometry is a combination of coordinates and geometry.
• A line can be drawn between any two points on the XY-plane.
• A line can be defined by the coordinates of any two points on that line.
• By combining different lines, we can draw various geometric figures. So line is a basic concept in coordinate geometry.
• In the next section, we will see more details about lines.
No comments:
Post a Comment