Chapter 2.8 - Solved Examples on Functions

In the previous section, we saw algebra of real functions. We saw some solved examples also. In this section, we will see a few more solved examples.

Solved example 2.34
Let R be the set of real numbers. Define the real function
f: R→R by f(x) = x + 10 and sketch the graph of this function.
Solution:
1. Given that f: R→R
So the input x values should be from R. The output f(x) values must also be present in R.
2. Let us input some convenient x values:
    ♦ When x = -10, f(x) = f(-10) = (-10 + 10) = 0
    ♦ When x = -9, f(x) = f(-9) = (-9 + 10) = 1
    ♦ When x = -7, f(x) = f(-7) = (-7 + 10) = 3
    ♦ When x = 0, f(x) = f(0) = (0 + 10) = 10
    ♦ When x = 2, f(x) = f(2) = (2 + 10) = 12
    ♦ When x = 3, f(x) = f(3) = (3 + 10) = 13
    ♦ When x = 4, f(x) = f(4) = (4 + 10) = 14
3. We can make a table using the above values:

Table.2.10

Such a table is convenient to plot the graph of the function.
4. The graph is shown in fig.2.20 below:

Fig.2.20

 

• We see that, the graph is a line.
• In our earlier analytical geometry classes, we have seen that:
Equation of a line takes the form y = mx + c, where m and c are constants.
• In our present case, the function is f(x) = x + 10. This is comparable to y = mx + c because:
    ♦ y is equivalent to f(x)
    ♦ m is equivalent to 1
    ♦ c is equivalent to 10
5. The function f defined by f(x) = mx + c, x ∈ R is called linear function.
• So our present case f(x) = x + 10 is a linear function.

Solved example 2.35
Let R be a relation from Q to Q defined by R = {(a, b) : a, b ∈ Q and a – b ∈ Z}. Show that
(i) (a, a) ∈ R for all a ∈ Q
(ii) (a, b) ∈ R implies that (b, a) ∈ R
(iii) (a, b) ∈ R and (b, c) ∈ R implies that (a, c) ∈ R
Solution:
1. Q is the set of rational numbers. A relation R is defined from Q to Q.
• Details about this relation R can be written as follows:
   ♦ The set R contains all ordered pairs (a, b) such that,
   ♦ a is a rational number,
   ♦ b is also a rational number,
   ♦ a-b is an integer.
2. Recall that,
   ♦ rational numbers can have a decimal part
   ♦ integers do not have a decimal part
3. We can write infinite pairs of rational numbers in such a way that their differences are integers.
• Let us see some examples:
   ♦ For the pair (3.157, 11.157), difference = (3.157 – 11.157) = -8
   ♦ For the pair (-2.73, 10.27), difference = (-2.73 – 10.27) = 13
• All such pairs are eligible to be included in the set R
• Now we can write the answers of the given questions.
Part (i):
• The pairs are in the form (a, a) and a is a rational number.
   ♦ Here both the elements are the same. Their difference (a-a) will be zero.
• Zero is an integer. So all pairs in the form (a, a), where a is a rational number, are eligible to be included in R.
• We can write: (a, a) ∈ R for all a ∈ Q
Part (ii):
• If a and b are such that a - b is an integer, then b – a will also be an integer.
An example:
• Consider the pair (3.157, 11.157)
   ♦ The difference (3.157 – 11.157) = -8
   ♦ The difference (11.157 – 3.157) = 8
Another example:
• Consider the pair (-2.73, 10.27)
   ♦ The difference (-2.73 – 10.27) = -13
   ♦ The difference (10.27 –  - 2.73) = 13
• So (b, a) will be eligible to be included in R
• We can write: (a,b) ∈ R implies that (b, a) ∈ R
Part (iii):
• We have to prove that, (a - c) is an integer if
   ♦ (a – b) gives an integer
   ♦ (b – c) also gives an integer,
• Let us see an example:
   ♦ Consider the pair (-2.73, 10.27)
   ♦ The difference (a – b) = (-2.73 – 10.27) = -13
   ♦ Consider the pair (10.27, 6.27)
   ♦ The difference (b – c) = (10.27 – 6.27) = 4
   ♦ Now the difference (a – c) = (-2.73 – 6.27) = -9
• So (a,c) is eligible to be included in R.
• We can prove this algebraically also:
   ♦ (a - b) + (b - c) = a - b + b - c = (a - c)
   ♦ (-2.73 – 10.27) + (10.27 – 6.27) = (-2.73 – 6.27)
• We can write: (a, b) ∈ R and (b, c) ∈ R implies that (a, c) ∈ R

Solved example 2.36
Let f = {(1,1), (2,3), (0, –1), (–1, –3)} be a linear function from Z into Z. Find f(x).
Solution:
1. Given that f is a linear function. So it will be in the form: f(x) = mx + c
All ordered pairs in the set f will satisfy this relation.
2. Consider the pair (1, 1). We get: 1 = m × 1 + c
⇒ 1 = m + c   
3. Consider the pair (2, 3). We get: 3 = m × 2 + c
⇒ 3 = 2m + c
4. Subtracting (2) from (3), we get:
3 - 1 = (2m + c) - (m + c)
⇒ 2 = m
5. Substituting for m in (2), we get: 1 = 2 + c
⇒ c = -1
6. Substituting for m and c in (1), we get: f(x) = 2x - 1
7. Note: We used the ordered pairs (1, 1) and (2, 3)
   ♦ It would be much more easier if we use (1, 1) and (0, -1)
   ♦ This is because, the term with m will become zero.

Solved example 2.37
Find the domain of the function $\mathbf\small{\rm{f(x)=\frac{x^2+3x+5}{x^2-5x+4}}}$
Solution:
1. Consider the denominator x² - 5x + 4
• If this denominator become zero, f(x) cannot be defined. So we must not input those x values which make x² - 5x + 4 zero.
2. So we need to find those x values which will make x² - 5x + 4 zero.
• For that, we equate it to zero and solve for x.
x² - 5x + 4 = 0
⇒ x² - 5x = -4
⇒ x² - 5x + (⁵⁄₂)² = -4 + (⁵⁄₂)²
⇒ (x - ⁵⁄₂)² = -4 + ²⁵⁄₄
⇒ (x - ⁵⁄₂)² = ⁹⁄₄
⇒ x- ⁵⁄₂ = ± ³⁄₂
⇒ x = (⁵⁄₂ + ³⁄₂) or (⁵⁄₂ - ³⁄₂)
⇒ x = ⁸⁄₂ or ²⁄₂
⇒ x = 4 or 1
3. So it is clear that, we must not use 4 and 1 as input x.
• We can write: domain = R - {4, 1}
• That means, domain is the set obtained by performing the 'difference' operation on the sets R and {4, 1}
   ♦ See difference of two sets.

Solved example 2.38
The function f is defined by:
$f(x) =
\begin{cases}
1-x,  & \text{if}\; x < 0 \\
1,  & \text{if}\; x = 0 \\
x+1, & \text{if} \; x > 0
\end{cases}$
Draw the graph of f(x).
Solution:
1. If we input an x value which is less than 0, that x value will be processed according to the function: f(x) = 1 - x
• Let us try some x values which are less than 0:
   ♦ When x = -5, f(x) = 1 - x = 1 - (-5) = 6
   ♦ When x = -3, f(x) = 1 - x = 1 - (-3) = 4
2. If we input an x value which is equal to 0, that x value will be processed according to the function: f(x) = 1
• Here there is no need to try different x values. Only one input x is possible and that is '0'.
• Also it is given that, when x = 0, f(x) = a constant, which is '1'.
• So there is no need to see how the x value is processed.
3. If we input an x value which is greater than 0, that x value will be processed according to the function: f(x) = x + 1
• Let us try some x values which are less than 0:
   ♦ When x = 2, f(x) = x + 1 = 2 + 1 = 3
   ♦ When x = 7, f(x) = x + 1 = 7 + 1 = 8
4. Based on the above steps, we can make a table:

Table 2.11

5. Using the table, we can draw the graph:

Fig.2.21

---

Link to some more solved examples is given below:

Solved examples 2.39 to 2.49

---

We have completed a discussion on relations and functions. In the next chapter, we will see trigonometric functions.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 3 - Trigonometric Functions

In the previous section, we completed a discussion on relations and functions. In this chapter, we will see trigonometric functions.

• We have seen the basics of trigonometry in our previous classes. Details here.
• We will start our present discussion by deriving some interesting trigonometric identities. They can be written in steps:

1. Fig.3.1 below shows a right triangle ABC

Fig.3.1

• The angle at A is x^o
2. Applying Pythagoras theorem, we have: AB² + BC² = AC²
3. Dividing both sides by AC², we get: $\mathbf\small{\rm{\frac{AB^2}{AC^2}+\frac{BC^2}{AC^2}=\frac{AC^2}{AC^2}}}$
4. But $\mathbf\small{\rm{\frac{AB}{AC}}}$ is cos x. Also $\mathbf\small{\rm{\frac{BC}{AC}}}$ is sin x
• So we get: (cos x)² + (sin x)² = 1
5. Thus we get our first identity: cos²x + sin²x = 1
6. Consider again the result in (2).
Dividing both sides by BC², we get: $\mathbf\small{\rm{\frac{AB^2}{BC^2}+\frac{BC^2}{BC^2}=\frac{AC^2}{BC^2}}}$
7. But $\mathbf\small{\rm{\frac{AB}{BC}}}$ is cot x. Also $\mathbf\small{\rm{\frac{AC}{BC}}}$ is cosec x
• So we get: (cot x)² + 1 = (cosec x)²
8. Thus we get our second identity: cot²x + 1 = cosec²x
9. Consider again the result in (2).
Dividing both sides by AB², we get: $\mathbf\small{\rm{\frac{AB^2}{AB^2}+\frac{BC^2}{AB^2}=\frac{AC^2}{AB^2}}}$
10. But $\mathbf\small{\rm{\frac{BC}{AB}}}$ is tan x. Also $\mathbf\small{\rm{\frac{AC}{AB}}}$ is sec x
• So we get: 1 + (tan x)² = (sec x)²
11. Thus we get our third identity: 1 + tan²x = sec²x

---

Let us see some solved examples:

Solved example 3.1
Prove that $\mathbf\small{\rm{(\csc\theta-\cot\theta)^2=\frac{1-\cos\theta}{1+\cos\theta}}}$
Solution:
• Consider the RHS.
• Multiplying both numerator and denominator by (1 - cos 𝜃), we get:
$$\begin{eqnarray}
RHS &=& \frac{(1-\cos\theta)(1-\cos\theta)}{(1+\cos\theta)(1-\cos\theta)}      \nonumber \\
\Rightarrow RHS &=& \frac{(1-\cos\theta)^2}{1-\cos^2\theta}=\frac{(1-\cos\theta)^2}{\sin^2\theta} \nonumber \\
&=& \frac{1-2\cos\theta+\cos^2 \theta}{\sin^2\theta}=\frac{1}{\sin^2\theta}-\frac{2\cos\theta}{\sin^2\theta}+\frac{\cos^2 \theta}{\sin^2\theta} \nonumber \\
&=& \csc^2 \theta-2\csc\theta \cot\theta+\cot^2\theta \nonumber \\
&=& (\csc \theta-\cot\theta)^2 = LHS \nonumber
\end{eqnarray}$$

Solved example 3.2
Prove that: $\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}=2\sec A$
Solution:
• Consider the RHS.
• Multiplying both numerator and denominator by (1 - sin A), we get:
$$\begin{eqnarray}
LHS &=& \frac{\cos A(1-\sin A)}{(1+\sin A)(1-\sin A)}+\frac{(1+\sin A)(1-\sin A)}{\cos A(1-\sin A)}     \nonumber \\
\Rightarrow LHS &=& \frac{\cos A(1-\sin A)}{1-\sin^2 A}+\frac{1-\sin^2 A}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{\cos A(1-\sin A)}{\cos^2 A}+\frac{\cos^2 A}{\cos A(1-\sin A)}\nonumber \\
&=& \frac{(1-\sin A)}{\cos A}+\frac{\cos A}{(1-\sin A)} \nonumber \\
&=& \frac{(1-\sin A)^2+\cos^2 A}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{(1-2\sin A+\sin^2 A)+\cos^2 A}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{1-2\sin A+(\sin^2 A+\cos^2 A)}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{1-2\sin A+1}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{2-2\sin A}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{2(1-\sin A)}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{2}{\cos A} \nonumber \\
&=& 2\sec A = RHS \nonumber
\end{eqnarray}$$

Solved example 3.3
Prove that $\frac{\tan\theta}{1-\cot\theta}+\frac{\cot\theta}{1-\tan\theta}=1+\sec\theta \csc\theta$
[Hint : Write the expression in terms of sin θ and cos θ]
Solution:
1. Consider the first term on LHS:
$$\begin{eqnarray}
\text{First term}&=& \frac{\tan\theta}{1-\cot\theta}\nonumber \\
&=& \frac{\frac{\sin\theta}{\cos\theta}}{1-\frac{\cos\theta}{\sin\theta}}\nonumber \\
&=& \frac{\frac{\sin\theta}{\cos\theta}}{\frac{\sin\theta-\cos\theta}{\sin\theta}}\nonumber \\
&=& \frac{\sin\theta}{\cos\theta}\times \frac{\sin\theta}{\sin\theta-\cos\theta}\nonumber \\
&=& \frac{\sin^2\theta}{\cos\theta(\sin\theta-\cos\theta)} \nonumber
\end{eqnarray}$$
2. Consider the second term of LHS:
\begin{eqnarray}
\text{Second term}&=& \frac{\cot\theta}{1-\tan\theta}\nonumber \\
&=& \frac{\frac{\cos\theta}{\sin\theta}}{1-\frac{\sin\theta}{\cos\theta}}\nonumber \\
&=& \frac{\frac{\cos\theta}{\sin\theta}}{\frac{\cos\theta-\sin\theta}{\cos\theta}}\nonumber \\
&=& \frac{\cos\theta}{\sin\theta}\times \frac{\cos\theta}{\cos\theta-\sin\theta}\nonumber \\
&=& \frac{\cos^2\theta}{\sin\theta(\cos\theta-\sin\theta)}\nonumber \\
&=& \frac{-\cos^2\theta}{\sin\theta(\sin\theta-\cos\theta)} \nonumber
\end{eqnarray}
3.Adding (1) and (2), we get:
\begin{eqnarray}
\text{LHS}&=& \frac{1}{(\sin\theta-\cos\theta)}\left[ \frac{\sin^2\theta}{\cos\theta}-\frac{\cos^2\theta}{\sin\theta}\right]\nonumber \\
&=& \frac{1}{(\sin\theta-\cos\theta)}\left[ \frac{\sin^3\theta-\cos^3\theta}{\sin\theta\cos\theta}\right]\nonumber \\
&=& \frac{1}{(\sin\theta-\cos\theta)}\left[ \frac{(\sin\theta-\cos\theta)(\sin^2\theta+\sin\theta\cos\theta+\cos^2\theta)}{\sin\theta\cos\theta}\right]\nonumber \\
[&\because& a^3-b^3=(a-b)(a^2+ab+b^2)]\nonumber \\
&=& \frac{(\sin^2\theta+\sin\theta\cos\theta+\cos^2\theta)}{\sin\theta\cos\theta}\nonumber \\
&=& \frac{(1+\sin\theta\cos\theta)}{\sin\theta\cos\theta}\nonumber \\
[&\because& \sin^2\theta+\cos^2\theta=1]\nonumber \\
&=& \frac{1}{\sin\theta\cos\theta}+1\nonumber \\
&=& 1+\sec\theta\csc\theta=RHS \nonumber
\end{eqnarray}

---

Link to some more solved examples is given below:

Solved examples 3.4 to 3.10

---

In the next section, we will see measurement of angles.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 2.7 - Algebra of Real Functions

In the previous section, we saw greatest integer function. In this section, we will see algebra of real functions. Algebra of real functions involves the following operations:
• Addition of two real functions.
• Subtraction of a real function from another real function.
• Multiply a real function by a scalar. (the scalar will be a real number)
• Multiply a real function by another real function.
• Divide a real function by another real function.

Addition of two real functions
This can be explained in 4 steps:
1. Consider a real function: f: X→R
• From the notation, it is clear that, the function is defined from a set X to the set R
• Set X should be a subset of set R
    ♦ For example, X can be the set of integers.
2. Consider another real function: g: X→R
• From the notation, it is clear that, the function is defined from a set X to the set R
• Set X should be the same X mentioned in 1
3. We can add the above two functions.
• The resulting function is denoted as: (f + g): X→R
• This resulting function is defined as:
(f + g) (x) = f(x) + g(x), for all x ∈ X
4. Let us see some examples:
Example 1:
Let f(x) = x² and g(x) = 2x + 1 be two real functions. Find (f + g) (x)
Solution:
• We have: (f + g) (x) = f(x) + g(x)
• So in our present case, we get:
(f + g) (x) = x² + 2x + 1
Example 2:
A real function f: X→R is defined as: f(x) = √x
Another real function g: X→R is defined as: g(x) = x
Where X is the set of non-negative real numbers. Find (f + g) (x)
Solution:
• We have: (f + g) (x) = f(x) + g(x)
• So in our present case, we get:
(f + g) (x) = √x + x
Note: In the question, it is specified that, X is the set of non-negative real numbers. So all  input x values will be non-negative real numbers only. If we input negative real numbers, √x will give imaginary numbers. So the function f(x) will not be a real function. The function (f + g) (x) will also be not a real function.

Subtraction of a real function from another real function
This can be explained in 4 steps:
1. Consider a real function: f: X→R
• From the notation, it is clear that, the function is defined from a set X to the set R
• Set X should be a subset of set R
    ♦ For example, X can be the set of integers.
2. Consider another real function: g: X→R
• From the notation, it is clear that, the function is defined from a set X to the set R
• Set X should be the same X mentioned in 1
3. We can subtract the second function from the first.
• The resulting function is denoted as: (f - g): X→R
• This resulting function is defined as:
(f - g) (x) = f(x) - g(x), for all x ∈ X
4. Let us see some examples:
Example 1:
Let f(x) = x² and g(x) = 2x + 1 be two real functions. Find (f - g) (x)
Solution:
• We have: (f - g) (x) = f(x) - g(x)
• So in our present case, we get:
(f - g) (x) = x² - 2x - 1
Example 2:
A real function f: X→R is defined as: f(x) = √x
Another real function g: X→R is defined as: g(x) = x
Where X is the set of non-negative real numbers. Find (f - g) (x)
Solution:
• We have: (f - g) (x) = f(x) - g(x)
• So in our present case, we get:
(f - g) (x) = √x - x
Note: In the question, it is specified that, X is the set of non-negative real numbers. So all  input x values will be non-negative real numbers only. If we input negative real numbers, √x will give imaginary numbers. So the function f(x) will not be a real function. The function (f - g) (x) will also be not a real function.

Multiplication of a real function by a scalar
This can be explained in 3 steps:
1. Consider a real function: f: X→R
• From the notation, it is clear that, the function is defined from a set X to the set R
• Set X should be a subset of set R
    ♦ For example, X can be the set of integers.
2. Consider a scalar 𝛼. Here 𝛼 is a real number
3. We can multiply the function in (1) by 𝛼.
• The resulting function is denoted as: (𝛼f): X→R
• This resulting function is defined as:
(𝛼f) (x) = 𝛼f(x), for all x ∈ X

Multiplication of two real functions
This can be explained in 5 steps:
1. Consider a real function: f: X→R
• From the notation, it is clear that, the function is defined from a set X to the set R
• Set X should be a subset of set R
    ♦ For example, X can be the set of integers.
2. Consider another real function: g: X→R
• From the notation, it is clear that, the function is defined from a set X to the set R
• Set X should be the same X mentioned in 1
3. We can multiply the above two functions.
• The resulting function is denoted as: (fg): X→R
• This resulting function is defined as:
(fg) (x) = f(x) g(x), for all x ∈ X
4. Let us see some examples:
Example 1:
Let f(x) = x² and g(x) = 2x + 1 be two real functions. Find (fg) (x)
Solution:
• We have: (fg) (x) = f(x) g(x)
• So in our present case, we get:
(fg) (x) = x² × (2x + 1) = 2x³ + x²
Example 2:
A real function f: X→R is defined as: f(x) = √x
Another real function g: X→R is defined as: g(x) = x
Where X is the set of non-negative real numbers. Find (fg) (x)
Solution:
• We have: (fg) (x) = f(x) g(x)
• So in our present case, we get:
(fg) (x) = √x × x = $\mathbf\small{\rm{x^{1/2} \times x = x^{1/2 + 1}=x^{3/2}}}$
Note: In the question, it is specified that, X is the set of non-negative real numbers. So all  input x values will be non-negative real numbers only. If we input negative real numbers, √x will give imaginary numbers. So the function f(x) will not be a real function. The function (fg) (x) will also be not a real function.
5. Multiplication of two real functions is also known as pointwise multiplication.

Quotient of two real functions
This can be explained in 4 steps:
1. Consider a real function: f: X→R
• From the notation, it is clear that, the function is defined from a set X to the set R
• Set X should be a subset of set R
    ♦ For example, X can be the set of integers.
2. Consider another real function: g: X→R
• From the notation, it is clear that, the function is defined from a set X to the set R
• Set X should be the same X mentioned in 1
3. We can divide the first function by the second function.
• The resulting function is denoted as: $\mathbf\small{\rm{\left(\frac{f}{g} \right):X\rightarrow R}}$
• This resulting function is defined as:
$\mathbf\small{\rm{\left(\frac{f}{g} \right)(x) =\frac{f(x)}{g(x)}}}$, provided g(x) ≠ 0, x ∈ X
4. Let us see some examples:
Example 1:
Let f(x) = x² and g(x) = 2x + 1 be two real functions. Find $\mathbf\small{\rm{\left(\frac{f}{g} \right)(x) }}$
Solution:
• We have: $\mathbf\small{\rm{\left(\frac{f}{g} \right)(x) =\frac{f(x)}{g(x)}}}$
• So in our present case, we get:
$\mathbf\small{\rm{\left(\frac{f}{g} \right)(x) =\frac{f(x)}{g(x)}=\frac{x^2}{2x+1}}}$
• Note that, in the denominator, we have (2x + 1). If the input x value is (-¹⁄₂), the whole denominator will become zero. So at x = (-¹⁄₂), the quotient function is not defined. We must mention this in the final answer.
• We can write:
$\mathbf\small{\rm{\left(\frac{f}{g} \right)(x) =\frac{x^2}{2x+1},\;x\ne -\frac{1}{2},\;x\in X}}$
Example 2:
A real function f: X→R is defined as: f(x) = √x
Another real function g: X→R is defined as: g(x) = x
Where X is the set of non-negative real numbers. Find $\mathbf\small{\rm{\left(\frac{f}{g} \right)(x) }}$
Solution:
• We have: $\mathbf\small{\rm{\left(\frac{f}{g} \right)(x) =\frac{f(x)}{g(x)}}}$
• So in our present case, we get:
$\mathbf\small{\rm{\left(\frac{f}{g} \right)(x) =\frac{f(x)}{g(x)}=\frac{\sqrt x}{x}=\frac{x^{1/2}}{x}=x^{(1/2 - 1)}=x^{-1/2}=\frac{1}{\sqrt x}}}$
• Note that, in the denominator, we have √x. If the input x value is zero, the whole denominator will become zero. So at x = 0, the quotient function is not defined. We must mention this in the final answer.
• We can write:
$\mathbf\small{\rm{\left(\frac{f}{g} \right)(x) =\frac{f(x)}{g(x)}=\frac{1}{\sqrt x},\;x \ne 0, \;x\in X}}$

---

Now we will see some solved examples related to the topic of functions as a whole.

Solved example 2.29
Which of the following relations are functions? Give reasons. If it is a function,
determine its domain and range.
(i) {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}
(ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)}
(iii) {(1,3), (1,5), (2,5)}.
Solution:
• Usually, a relation is defined from a set A to set B. Or from a set A to itself.
• But here, we are not given A or B. So we will assume that, all the elements of A are present as first elements in R.
• If all elements are not present, we will be able to straight away say that, they are not functions.
• Thus in all the three questions, we need to check the second condition only.
Part (i):
• All the first elements appear only once. So it is a function.
    ♦ Domain of f = {2, 5, 8, 11, 14, 17}
    ♦ Range of f = {1}
Part (ii):
• All the first elements appear only once. So it is a function.
    ♦ Domain of f = {2, 4, 6, 8, 10, 12, 14}
    ♦ Range of f = {1, 2, 3, 4, 5, 6, 7}
Part (iii):
• The first element '1' appear more than once. So it is not a function.

Solved example 2.30
Find the domain and range of the following real functions:
(i) f(x) = - |x|
(ii) f(x) = √(9 - x²)
Solution:
Part (i): f(x) = - |x|
1. Given that, this is a real function. So all input x must be real numbers.
2. |x| on the right side indicates that, what ever be the input x, it's modulus will be taken. Modulus values are positive numbers.
3. But there is also a negative sign on the right side. So all the positive values derived from |x| will be converted to negative numbers. All those negative numbers will be real values.
4. Let us see some examples:
    ♦ Let input x be -5. Then f(x) = -|x| = -|-5| = -5
    ♦ Let input x be +4. Then f(x) = -|x| = -|4| = -4
5. It is clear that:
    ♦ Input x values can be negative or positive.
    ♦ Output f(x) values will be negative
6. Input x values can be any real number. So we can write:
Domain = {x : x ∈ R}
• That means,
    ♦ Domain is the set of all x such that,
    ♦ x is an element of R
• We can write in a simpler form also: Domain = R
7. Output f(x) values will be negative real numbers. So we can write:
Range = {y : y ∈ R^-}
• That means,
    ♦ Range is the set of all y such that,
    ♦ y is an element of R^-
• We can write in a simpler form also: Range = R^-
8. Another way to write range:
• We have seen intervals as sets. (See fig.1.3 of section 1.4)
• In our present case, the range does not contain all numbers on the real number line.
    ♦ The range contains only an interval in the real number line.
    ♦ That interval starts from -∞ and ends at 0
• This interval can be written in set form as: (-∞, 0]
    ♦ So we can write: Range = (-∞, 0]
• This indicates that:
    ♦ Every real number between -∞ and 0 will be an f(x) value.
    ♦ -∞ cannot be an f(x) value. (note the '(' on the left side of -∞)
    ♦ 0 can be an f(x) value. (note the ']' on the right side of 0)
9. Fig.2.18 below shows the graph of this function:

Fig.2.18

• We can mark any point on the two lines. It's y coordinate will be negative.

Part (ii): f(x) = √(9 - x²)
1. Given that, this is a real function. So all input x must be real numbers.
2. On the right side, we have a square root. The portion inside the square root symbol, should not become negative. Because, square root of negative numbers are imaginary numbers. They are not real numbers. So if the portion inside the square root symbol becomes negative, the function will not be real.
3. It is clear that, the portion inside the square root symbol must be zero or greater than zero. First we will see when it becomes zero. For that, we equate it to zero. We get:
9 - x² = 0
⇒ x² = 9
⇒ x = +3 or -3
So the portion becomes zero when x = +3 or -3
4. If x is greater than +3, the portion will become negative. So a value greater than +3 cannot be allowed.
• Also, if x is less than -3, the portion will become negative. So a value less than -3 cannot be allowed.
• Thus we get: Domain = [-3,3]
• That means:
    ♦ Every real number between -3 and +3 can be an input x value.
    ♦ -3 can be an input x value. (note the '[' on the left side of -3)
    ♦ +3 can be an input x value. (note the ']' on the right side of 3)
5. Next we will find the range.
• We see that, f(x) is obtained by subtracting a quantity from 9, and then taking the square root.
• If zero is subtracted from 9, then f(x) will be maximum. We get:
f(x) = √(9 - x²) = √(9 - 0²) = √(9 - 0) = √9 = +3
• If 9 is subtracted from 9, then f(x) will be zero. We get:
f(x) = √(9 - x²) = √(9 - 3²) = √(9 - 9) = √(9 - 9) = 0
• So the maximum value of f(x) possible is +3 and the minimum possible is 0.
• Thus we can write: Range = [0,3]
• That means:
    ♦ Every real number between 0 and +3 will be a f(x) value.
    ♦ 0 will be a f(x) value.
    ♦ +3 will be a f(x) value.
6. Fig.2.19 below shows the graph of this function:

Fig.2.19

 

Solved example 2.31
A function f is defined by f(x) = 2x –5. Write down the values of
(i) f(0), (ii) f(7), (iii) f(–3).
Solution:
(i) f(0) = (2 × 0) - 5 = (0 - 5) = -5
(ii) f(7) = (2 × 7) - 5 = (14 - 5) = 9
(iii) f(-3) = (2 × -3) - 5 = (-6 - 5) = -11

Solved example 2.32
The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by $\mathbf\small{\rm{t(C)=\frac{9C}{5}+32}}$
Find (i) t(0) (ii) t(28) (iii) t(–10) (iv) The value of C, when t(C) = 212.
Solution:
(i) $\mathbf\small{\rm{t(0)=\frac{9 \times 0}{5}+32}}$ = (0 + 32) = 32
(ii) $\mathbf\small{\rm{t(28)=\frac{9 \times 28}{5}+32}}$ = (50.4 + 32) = 82.4
(iii) $\mathbf\small{\rm{t(-10)=\frac{9 \times -10}{5}+32}}$ = (-18 + 32) = 14
(iv) $\mathbf\small{\rm{t(C)=200 =\frac{9 \times C}{5}+32}}$
⇒ 212 = 1.8C + 32
⇒ 1.8C = (212 - 32) = 180
⇒ C = ¹⁸⁰⁄_1.8  = 100

Solved example 2.33
Find the range of each of the following functions.
(i) f(x) = 2 – 3x, x ∈ R, x > 0.
(ii) f(x) = x² + 2, x is a real number.
(iii) f(x) = x, x is a real number.
Solution:
Part (i):
1. Given that: x ∈ R and x > 0.
    ♦ So the input x must be a real number,
    ♦ Also the input x must be positive and greater than zero.
2. Smallest possible input x will be that value which is very close to zero.
• Let us put x = 0. We will get: f(0) = (2 - (3 × 0)) = 2
    ♦ But this '2' cannot be accepted as a range value because we cannot use x = 0
• Let us put x = 1. We will get: f(1) = (2 - (3 × 1)) = (2 - 3) = -1
• Let us put x = 2. We will get: f(2) = (2 - (3 × 2)) = (2 - 6) = -4
• Let us put x = 3. We will get: f(3) = (2 - (3 × 3)) = (2 - 9) = -7
3. We see that, as input x increases, the value of f(x) decreases.
• Proceeding like this, we will reach f(x) = -∞ for a very large value of x.
4. So the range will be (-∞, 2)
• That means:
    ♦ Every real number between -∞ and +2 will be a f(x) value.
    ♦ -∞ will not be a f(x) value. (note the '(' on the left side of -∞)
    ♦ +2 will not be a f(x) value. (note the ')' on the right side of +2)

---

In the next section, we will see a few more solved examples.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 2.6 - Greatest Integer Function

In the previous section, we saw modulus function and signum function. In this section, we will see greatest integer function.

G. Greatest integer function
• The greatest integer function is a real valued function f: R→R defined as:
$\mathbf\small{\rm{f(x)=\left\lfloor x\right\rfloor }}$
• Details can be written in 10 steps:
1. Given that, it is a real valued function. That means, all values obtained after processing, must be real values.
2. Whatever be the value of input x, the output will be $\mathbf\small{\rm{\left\lfloor x\right\rfloor }}$
This can be explained in 4 steps:
(i) $\mathbf\small{\rm{\left\lfloor x\right\rfloor }}$ is an integer.
   ♦ An integer is a positive or negative real number.
   ♦ But it cannot have fractional or decimal parts.
(ii) The integer obtained by $\mathbf\small{\rm{\left\lfloor x\right\rfloor }}$ must not be greater than the input x
(iii) The integer obtained by $\mathbf\small{\rm{\left\lfloor x\right\rfloor }}$ can be equal to the input x
(iv) The integer obtained by $\mathbf\small{\rm{\left\lfloor x\right\rfloor }}$ must be the largest possible integer which is lesser than the input x
• For each input x, we must examine each of the above four conditions.
3. Let us see some examples:
Example 1:
This can be written in 6 steps:
(i) Let the input x be 4.7
• So the output, which is f(x), will be $\mathbf\small{\rm{\left\lfloor 4.7\right\rfloor }}$
(ii) Applying the first condition, $\mathbf\small{\rm{\left\lfloor 4.7\right\rfloor }}$ will be an integer.
(iii) Applying the second condition, $\mathbf\small{\rm{\left\lfloor 4.7\right\rfloor }}$ will not be greater than 4.7
   ♦ So all integers 5, 6, 7, . . . can be ruled out.
(iv) Applying the third condition, $\mathbf\small{\rm{\left\lfloor 4.7\right\rfloor }}$ can be equal to 4.7
   ♦ But 4.7 is not an integer. So this condition is not applicable.
(v) Applying the fourth condition, $\mathbf\small{\rm{\left\lfloor 4.7\right\rfloor }}$ will be equal to 4
(vi) So we can write:
When x = 4.7, f(x) = $\mathbf\small{\rm{\left\lfloor x\right\rfloor = \left\lfloor 4.7\right\rfloor }}$ = 4

Example 2:
This can be written in 6 steps:
(i) Let the input x be 11.99
• So the output, which is f(x), will be $\mathbf\small{\rm{\left\lfloor 11.99\right\rfloor }}$
(ii) Applying the first condition, $\mathbf\small{\rm{\left\lfloor 11.99\right\rfloor }}$ will be an integer.
(iii) Applying the second condition, $\mathbf\small{\rm{\left\lfloor 11.99\right\rfloor }}$ will not be greater than 11.99
   ♦ So all integers 12, 13, 14, . . . can be ruled out.
(iv) Applying the third condition, $\mathbf\small{\rm{\left\lfloor 11.99\right\rfloor }}$ can be equal to 11.99
   ♦ But 11.99 is not an integer. So this condition is not applicable.
(v) Applying the fourth condition, $\mathbf\small{\rm{\left\lfloor 11.99\right\rfloor }}$ will be equal to 11
(vi) So we can write:
When x = 11.99, f(x) = $\mathbf\small{\rm{\left\lfloor x\right\rfloor = \left\lfloor 11.99\right\rfloor }}$ = 11

Example 3:
This can be written in 6 steps:
(i) Let the input x be -3.58
• So the output, which is f(x), will be $\mathbf\small{\rm{\left\lfloor -3.58\right\rfloor }}$
(ii) Applying the first condition, $\mathbf\small{\rm{\left\lfloor -3.58\right\rfloor }}$ will be an integer.
(iii) Applying the second condition, $\mathbf\small{\rm{\left\lfloor -3.58\right\rfloor }}$ will not be greater than -3.58
   ♦ So all integers -2, -1, 0, 1, 2, 3, 4, . . . can be ruled out.
(iv) Applying the third condition, $\mathbf\small{\rm{\left\lfloor -3.58\right\rfloor }}$ can be equal to -3.58
   ♦ But -3.58 is not an integer. So this condition is not applicable.
(v) Applying the fourth condition, $\mathbf\small{\rm{\left\lfloor -3.58\right\rfloor }}$ will be equal to -4
(vi) So we can write:
When x = -3.58, f(x) = $\mathbf\small{\rm{\left\lfloor x\right\rfloor = \left\lfloor -3.58\right\rfloor }}$ = -4    

Example 4:
This can be written in 5 steps:
(i) Let the input x be 8
• So the output, which is f(x), will be $\mathbf\small{\rm{\left\lfloor 8\right\rfloor }}$
(ii) Applying the first condition, $\mathbf\small{\rm{\left\lfloor 8\right\rfloor }}$ will be an integer.
(iii) Applying the second condition, $\mathbf\small{\rm{\left\lfloor 8\right\rfloor }}$ will not be greater than 8
   ♦ So all integers 9, 10, 11, 12, . . . can be ruled out.
(iv) Applying the third condition, $\mathbf\small{\rm{\left\lfloor 8\right\rfloor }}$ can be equal to 8
   ♦ 8 is indeed an integer. So this condition is applicable.
(v) So we can write:
When x = 8, f(x) = $\mathbf\small{\rm{\left\lfloor x\right\rfloor = \left\lfloor 8\right\rfloor }}$ = 8

Example 5:
This can be written in 5 steps:
(i) Let the input x be -7
• So the output, which is f(x), will be $\mathbf\small{\rm{\left\lfloor -7\right\rfloor }}$
(ii) Applying the first condition, $\mathbf\small{\rm{\left\lfloor -7\right\rfloor }}$ will be an integer.
(iii) Applying the second condition, $\mathbf\small{\rm{\left\lfloor -7\right\rfloor }}$ will not be greater than -7
   ♦ So all integers 9, 10, 11, 12, . . . can be ruled out.
(iv) Applying the third condition, $\mathbf\small{\rm{\left\lfloor -7\right\rfloor }}$ can be equal to -7
   ♦ -7 is indeed an integer. So this condition is applicable.
(v) So we can write:
When x = -7, f(x) = $\mathbf\small{\rm{\left\lfloor x\right\rfloor = \left\lfloor -7\right\rfloor }}$ = -7
4. Proceeding like this, we will get infinite number of ordered pairs. All those ordered pairs should be included in the set f.
• So we can write: f = {. . . , (-7,-7), (-3.58, -4), (4.7, 4), (8, 8), (11.99, 11), . . .}
5. The above set f is written in roster form. But we have to remember an important point. It can be written in 3 steps:
(i) Both elements of the ordered pairs are real numbers.
• The second element y can take only integers (set Z). So we need not worry about y values.
(ii) Since x value can be any real number, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them.
(iii) So it is better to use set builder form to write f.
6. In the set builder form, we can write:
f = {(x,y) : x ∈ R, y ∈ Z}
• That means:
    ♦ The set f contains all ordered pairs (x,y) such that,
    ♦ x is a real number,
    ♦ y is an integer
7. Once we write the set f, we can write the domain and range of f.
(i) First we will write the domain:
• Domain of f is the set containing all the first elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of first elements.
• We saw that all the first elements are real numbers. Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Domain of f = {x : x ∈ R}
• That means:
    ♦ The domain of f will contain all real numbers.
(ii) Next we will write the range:
• Range of f is the set containing all the second elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of second elements.
• We saw that the second elements can be only integers.
• We can write all integers in a definite pattern. So we can use the roster form.
• We can write:
    ♦ Range of f = {. . . , -3, -2, -1, 0, 1, 2, 3, 4, . . .}
• We can write it in the set builder form also:
    ♦ Range of f = {y: y ∈ Z}
• That means:
    ♦ The domain of f will contain all y such that, y is an integer.
8. We can make a table using the x and y values in the set f. Such a table is convenient to draw the graph of the function.
• Note that, to input for x, we choose convenient numbers from the set R.
• It is better not to choose numbers with recurring decimals. They will be difficult to plot.

Table 2.9

9. The red lines in fig.2.17(a) below, is the graph of the function.

Fig.2.17

• The reader is advised to prepare a table and draw the graph in his/her own graph books.
• We can write some peculiarities of these red lines. They can be written in 4 steps:
(i) The lines are small segments. They do not extend to infinity.
(ii) Consider the green vertical dashed line in fig.b. This line is drawn at x = 3.25
• That means, we are giving an input x value of 3.25
• When this x value is processed, we get the f(x) as 3
• Whatever real value (between 3 and 4) that we input for x, we will get f(x) as 3
   ♦ All y values in that red segment are indeed 3
   ♦ If the x value is not between 3 and 4, this red segment is not applicable.
• What if the x value is 4?
   ♦ Remember that, if x = 4, f(x) will be 4.
   ♦ This red segment do not have y = 4
   ♦ So if the x value is 4, this red segment is not applicable.
         ✰ We have to look at the next higher red segment.
   ♦ That is why a hollow circle is given at the right end of this red segment.
(iii) Consider the magenta vertical dashed line in fig.b. This line is drawn at x = -1.5
• That means, we are giving an input x value of -1.5
• When this x value is processed, we get the f(x) as -2
• Whatever real value (between -2 and -1) that we input for x, we will get f(x) as -2
   ♦ All y values in that red segment are indeed -2
   ♦ If the x value is not between -2 and -1, this red segment is not applicable.
• What if the x value is -1?
   ♦ Remember that, if x = -1, f(x) will be -1.
   ♦ This red segment do not have y = -1
   ♦ So if the x value is -1, this red segment is not applicable.
         ✰ We have to look at the next higher red segment.
   ♦ That is why a hollow circle is given at the right end of this red segment.
10. The greatest integer function is also known as step function because, it's graph looks like steps. This function has many applications in science and engineering.

---

In the next section, we will see algebra of real functions.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 2.5 - Modulus Function And Signum Function

In the previous section, we saw rational function. In this section, we will see Modulus function and Signum function.

E. Modulus function
• A modulus function is a real valued function f: R→R defined by:
$\mathbf\small{\rm{f(x)=|x|}}$
• Details can be written in 12 steps:
1. Given that, it is a real valued function. That means, all values obtained after processing, must be real values.
2. Whatever be the value of x, the y value will be the modulus of that x value.
• This can be explained in two steps:
(i) If we take a positive number for input x, we must first write the modulus of that number. The y value will be this modulus.
    ♦ For example, let us take '8' for input x. The modulus of 8 = |8| = 8
    ♦ So f(x) = 8
(ii) If we take a negative number for input x, then also we must first write the modulus of that number. The y value will be this modulus.
    ♦ For example, let us take '-7' for input x. The modulus of -7 = |-7| = 7
    ♦ So f(x) = 7
3. The above information can be written in algebraic form as:
$f(x) =
\begin{cases}
x,  & \text{if}\; x \geq 0 \\
-x, & \text{if} \; x\lt 0
\end{cases}$
• We see two conditions on the right side of the curly bracket.
    ♦ The first condition is same as what we wrote in 2(i)
    ♦ The second condition is same as what we wrote in 2(ii)
• The second condition needs special attention. It has a '-' sign in front of 'x'. It will become clear if we consider an example:
   ♦ Let us take input x as -7
   ♦ Then f(x) = -x = -(x) = -(-7) = 7
   ♦ So the '-' sign is important.
4. The function can be defined by writing the ordered pairs which satisfy that function.
• So our next task is to find those ordered pairs.
5. It is given that, f : R→R
• This indicates that,
   ♦ the first elements of the ordered pairs (input x values) should be taken from the set R.
   ♦ the second elements (resulting y values) should be present in the set R
6. The set R is the set of real numbers. It will include integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. In short, R will contain every value which can be plotted on a number line. Recall that we plotted √2, √5, π etc., in our previous classes.
• Since different types of numbers are present in R, we will choose some convenient numbers at random.
• Let x = -7
   ♦ This x is processed as follows:
   ♦ Here x < 0. So we use the second condition
   ♦ f(x) = -x = -(x) = -(-7) = 7
   ♦ f(x) = f(-7) is the 'y value' when 'x value' is -7
   ♦ So we get an ordered pair (x,y) as: (-7, 7)
• Let x = -5
   ♦ This x is processed as follows:
   ♦ Here x < 0. So we use the second condition
   ♦ f(x) = -x = -(x) = -(-5) = 5
   ♦ f(x) = f(-5) is the 'y value' when 'x value' is -5
   ♦ So we get another ordered pair (x,y) as: (-5, 5)
• Let x = 0
   ♦ This x is processed as follows:
   ♦ Here x ≥ 0. So we use the first condition
   ♦ f(x) = x = 0
   ♦ f(x) = f(0) is the 'y value' when 'x value' is 0
   ♦ So we get another ordered pair (x,y) as: (0, 0)
• Let x = 2
   ♦ This x is processed as follows:
   ♦ Here x ≥ 0. So we use the first condition
   ♦ f(x) = x = 2
   ♦ f(x) = f(2) is the 'y value' when 'x value' is 2
   ♦ So we get another ordered pair (x,y) as: (2, 2)
• Let x = 5
   ♦ This x is processed as follows:
   ♦ Here x ≥ 0. So we use the first condition
   ♦ f(x) = x = 5
   ♦ f(x) = f(5) is the 'y value' when 'x value' is 5
   ♦ So we get another ordered pair (x,y) as: (5, 5)
• We see that, whatever be the value of x, the value of y will be the modulus of that x value.
7. Proceeding like this, we will get infinite number of ordered pairs. All those ordered pairs should be included in the set f.
• So we can write: f = {. . . , (-7,7), (-5, 5), (0, 0), (2, 2), (5, 5), . . .}
8. The above set f is written in roster form. But we have to remember an important point. It can be written in 3 steps:
(i) Both elements of the ordered pairs are real numbers.
(ii) Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them.
(iii) So it is better to use set builder form to write f.
9. In the set builder form, we can write:
f = {(x,y) : x ∈ R, y = |x|, |x| ∈ R}
• That means:
    ♦ The set f contains all ordered pairs (x,y) such that,
    ♦ x is a real number,
    ♦ y is the modulus of x,
    ♦ modulus of x is a real number
10. Once we write the set f, we can write the domain and range of f.
(i) First we will write the domain:
• Domain of f is the set containing all the first elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of first elements.
• We saw that all the first elements are real numbers. Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Domain of f = {x : x ∈ R}
• That means:
    ♦ The domain of f will contain all real numbers.
(ii) Next we will write the range:
• Range of f is the set containing all the second elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of second elements.
• We saw that all the first elements are real numbers. Since the second elements are moduli, there will not be any negative numbers. But there will be integers, fractions, decimals, recurring decimals etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Range of f = {x : x ∈ R⁺}
• That means:
    ♦ The range of f will contain all positive real numbers.
11. We can make a table using the x and y values in the set f. Such a table is convenient to draw the graph of the function.
• Note that, to input for x, we choose convenient numbers from the set R.
• It is better not to choose numbers with recurring decimals. They will be difficult to plot.

Table 2.7

12. The red lines in fig.2.15(a) below, is the graph of the function.

Fig.2.15

• The reader is advised to prepare a table and draw the graph in his/her own graph books.
• We can write some peculiarities of these red lines. They can be written in 4 steps:
(i) The red lines of f(x) = |x| always pass through the origin (0,0)
(ii) Mark any point on the red lines. Note the coordinates of that point.
   ♦ The y coordinate will be the modulus of the x coordinate.
   ♦ This is shown in fig.b
   ♦ The green vertical dashed line shows 8
         ✰ The green horizontal dashed line shows the modulus 8
   ♦ The magenta vertical dashed line shows -6
         ✰ The magenta horizontal dashed line shows the modulus 6
(iii) The red lines never go below the x axis. This is because, there will never be any negative y values.
(iv) We see arrows at both ends of the red lines.
• The left arrow indicates that:
The line can extend up to a point where x = -∞ and y = modulus of that x value.
• The right arrow indicates that:
The line can extend up to a point where x = +∞ and y = modulus of that x value.

F. Signum function
• A signum function is a real valued function f: R→R defined by three conditions:
$f(x) =
\begin{cases}
1,  & \text{if}\; x > 0 \\
0, & \text{if} \; x = 0 \\
-1, & \text{if} \; x < 0
\end{cases}$
• Details can be written in 12 steps:
1. Given that, it is a real valued function. That means, all values obtained after processing, must be real values.
2. Whatever be the value of x, we must examine each of the three conditions.
• This can be explained in three steps:
(i) If we take a positive number for input x, the y value will be 1
    ♦ For example, let us take '8' for input x. Then y = f(x) = 1
(ii) If we take zero for input x, the y value will be 0
(iii) If we take a negative number for input x, the y value will be -1
    ♦ For example, let us take '-6' for input x. Then y = f(x) = -1
3. The function can be defined by writing the ordered pairs which satisfy that function.
• So our next task is to find those ordered pairs.
4. It is given that, f : R→R
• This indicates that,
   ♦ the first elements of the ordered pairs (input x values) should be taken from the set R.
   ♦ the second elements (resulting y values) should be present in the set R
5. The set R is the set of real numbers. It will include integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. In short, R will contain every value which can be plotted on a number line. Recall that we plotted √2, √5, π etc., in our previous classes.
• Since different types of numbers are present in R, we will choose some convenient numbers at random.
• Let x = -7
   ♦ This x is processed as follows:
   ♦ Here x < 0. So we use the third condition
   ♦ f(x) = -1
   ♦ f(x) = f(-7) is the 'y value' when 'x value' is -7
   ♦ So we get an ordered pair (x,y) as: (-7, -1)
• Let x = -5
   ♦ This x is processed as follows:
   ♦ Here x < 0. So we use the third condition
   ♦ f(x) = -1
   ♦ f(x) = f(-5) is the 'y value' when 'x value' is -5
   ♦ So we get another ordered pair (x,y) as: (-5, -1)
• Let x = 0
   ♦ This x is processed as follows:
   ♦ Here x = 0. So we use the second condition.
   ♦ f(x) = x = 0
   ♦ f(x) = f(0) is the 'y value' when 'x value' is 0
   ♦ So we get another ordered pair (x,y) as: (0, 0)
• Let x = 2
   ♦ This x is processed as follows:
   ♦ Here x > 0. So we use the first condition
   ♦ f(x) = 1
   ♦ f(x) = f(2) is the 'y value' when 'x value' is 2
   ♦ So we get another ordered pair (x,y) as: (2, 1)
• Let x = 5
   ♦ This x is processed as follows:
   ♦ Here x > 0. So we use the first condition
   ♦ f(x) = 1
   ♦ f(x) = f(5) is the 'y value' when 'x value' is 5
   ♦ So we get another ordered pair (x,y) as: (5, 1)
• We see that,
    ♦ If the input x is a positive value, y will be +1
    ♦ If the input x is zero, y will be zero
    ♦ If the input x is a negative value, y will be -1
6. Proceeding like this, we will get infinite number of ordered pairs. All those ordered pairs should be included in the set f.
• So we can write: f = {. . . , (-7,-1), (-5, -1), (0, 0), (2, 1), (5, 1), . . .}
7. The above set f is written in roster form. But we have to remember an important point. It can be written in 3 steps:
(i) Both elements of the ordered pairs are real numbers.
• The second element y can take only three values 1, 0 and -1. So we need not worry about y values.
(ii) Since x value can be any real number, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them.
(iii) So it is better to use set builder form to write f.
8. In the set builder form, we can write:
f = {(x,y) : x ∈ R, y = +1 if x > 0,  y = 0 if x = 0, y = -1 if x < 0}
• That means:
    ♦ The set f contains all ordered pairs (x,y) such that,
    ♦ x is a real number,
    ♦ y can be +1, 0 or -1
9. Once we write the set f, we can write the domain and range of f.
(i) First we will write the domain:
• Domain of f is the set containing all the first elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of first elements.
• We saw that all the first elements are real numbers. Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Domain of f = {x : x ∈ R}
• That means:
    ♦ The domain of f will contain all real numbers.
(ii) Next we will write the range:
• Range of f is the set containing all the second elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of second elements.
• We saw that the second elements can be only +1, 0 or -1.
   ♦ There will be infinite number of +1
   ♦ There will be only one 0
   ♦ There will be infinite number of +1
• But when we write a set, repeating elements are written only once. So we can easily write in roster form.
• We can write:
    ♦ Range of f = {1, 0, -1}
10. We can make a table using the x and y values in the set f. Such a table is convenient to draw the graph of the function.
• Note that, to input for x, we choose convenient numbers from the set R.
• It is better not to choose numbers with recurring decimals. They will be difficult to plot.

Table 2.8

11. The red lines in fig.2.16(a) below, is the graph of the function.

Fig.2.16

• The reader is advised to prepare a table and draw the graph in his/her own graph books.
• We can write some peculiarities of these red lines. They can be written in 4 steps:
(i) The top red line is obtained when we use positive x values for input.
• This line never goes to the left side of the y axis because, no negative x values are used for this line.
• In fact, this line do not even touch the y axis. Because, (x = 0) is not used for this line. Remember that this line is for x > 0. That means, only those values which are greater than zero can be used for this line.
• Since it cannot touch the y axis, a hollow red circle is given at the left end of this line. The hollow red circle indicates that, the point inside the circle is not included in the graph.
(ii) The red filled circle at (0, 0) is obtained when we use (x = 0) for input.
• Even if it is a single point, it is a graph. It is the graph satisfying the second condition.
• We can write:
The graph satisfying the second condition contains only one point.
(iii) The bottom red line is obtained when we use negative x values for input.
• This line never goes to the right side of the y axis because, no positive x values are used for this line.
• In fact, this line do not even touch the y axis. Because, (x = 0) is not used for this line. Remember that this line is for x < 0. That means, only those values which are lesser than zero can be used for this line.
• Since it cannot touch the y axis, a hollow red circle is given at the right end of this line. The hollow red circle indicates that, the point inside the circle is not included in the graph.
(iv) Mark any point on the red lines. Note the coordinates of that point.
   ♦ The y coordinate will be either -1 or +1
   ♦ This is shown in fig.b
   ♦ The green vertical dashed line shows 1.5
         ✰ This line meets the red line at a point where y coordinate is +1
   ♦ The magenta vertical dashed line shows -1.25
         ✰ This line meets the red line at a point where the y coordinate is -1
(v) We see one arrow each for the top and bottom red lines.
• The arrow of the top red line indicates that:
The line can extend up to a point where x = +∞ and y = +1
• The arrow of the bottom red line indicates that:
The line can extend up to a point where x = -∞ and y = -1
12. The signum function has many applications in science and engineering.
• If the output of a mathematical calculation process is +1, a machine can be instructed to start operation.
• If the output of a mathematical calculation process is -1, the machine can be instructed to stop operation.
• Let us see an example. It can be written in steps:
(i) Consider the function: $\mathbf\small{\rm{f(x)=\frac{x}{|x|}}}$
(ii) Let input x be -4
• Then $\mathbf\small{\rm{f(-4)=\frac{-4}{|-4|}=\frac{-4}{4}}}$ = -1
   ♦ The machine will stop operation.
(iii) Let input x be +7
• Then $\mathbf\small{\rm{f(+7)=\frac{+7}{|+7|}=\frac{+7}{7}}}$ = +1
   ♦ The machine will start operation.

---

In the next section, we will see Greatest integer function.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 2.4 - Rational Function

In the previous section, we saw constant function and polynomial function. In this section, we will see rational function.

D. Rational function
• A rational function is a real valued function f: R→R defined by:
$\mathbf\small{\rm{f(x)=\frac{p(x)}{q(x)}}}$
• Details can be written in 11 steps:
1. Given that, it is a real valued function. That means, all values obtained after processing, must be real values.
2. Let us examine the numerator and denominator:
• The numerator is p(x). It must be a polynomial function.
• The denominator is q(x). It must also be a polynomial function.
   ♦ This q(x) should not be equal to zero.
   ♦ If it is zero, the function f(x) cannot be defined.
3. The function can be defined by writing the ordered pairs which satisfy that function.
• So our next task is to find those ordered pairs.
• We will take a simple rational function: f(x) = $\mathbf\small{\rm{\frac{1}{x}}}$
    ♦ Recall that all constants are polynomials. So '1' is a polynomial.
    ♦ For example, 4 can be written as: 4x⁰, which is (4 × 1) = 4
4. It is given that, f : R→R
• This indicates that,
   ♦ the first elements of the ordered pairs (input x values) should be taken from the set R.
   ♦ the second elements (resulting y values) should be present in the set R
5. The set R is the set of real numbers. It will include integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. In short, R will contain every value which can be plotted on a number line. Recall that we plotted √2, √5, π etc., in our previous classes.
• Since different types of numbers are present in R, we will choose some convenient numbers at random.
• Let x = -7
   ♦ This x is processed as follows:
   ♦ f(-7) = $\mathbf\small{\rm{\frac{1}{(-7)}}}$ = -0.143
   ♦ f(-7) is the 'y value' when 'x value' is -7
   ♦ So we get an ordered pair (x,y) as: (-7, -0.143)
• Let x = -5
   ♦ This x is processed as follows:
   ♦ f(-5) = $\mathbf\small{\rm{\frac{1}{(-5)}}}$ = -0.2
   ♦ f(-5) is the 'y value' when 'x value' is -5
   ♦ So we get an ordered pair (x,y) as: (-5, -0.2)
• Let x = 1
   ♦ This x is processed as follows:
   ♦ f(1) = $\mathbf\small{\rm{\frac{1}{(1)}}}$ = 1
   ♦ f(1) is the 'y value' when 'x value' is 1
   ♦ So we get an ordered pair (x,y) as: (1, 1)
• Let x = 2
   ♦ This x is processed as follows:
   ♦ f(2) = $\mathbf\small{\rm{\frac{1}{(2)}}}$ = 0.5
   ♦ f(2) is the 'y value' when 'x value' is 2
   ♦ So we get an ordered pair (x,y) as: (2, 0.5)
• Let x = 5
   ♦ This x is processed as follows:
   ♦ f(5) = $\mathbf\small{\rm{\frac{1}{(5)}}}$ = 0.2
   ♦ f(5) is the 'y value' when 'x value' is 0.2
   ♦ So we get an ordered pair (x,y) as: (5, 0.2)
• Let x = 10
   ♦ This x is processed as follows:
   ♦ f(10) = $\mathbf\small{\rm{\frac{1}{(10)}}}$ = 0.1
   ♦ f(10) is the 'y value' when 'x value' is 10
   ♦ So we get an ordered pair (x,y) as: (10, 0.1)
• We see that, whatever be the value of x, the value of y will be the reciprocal of that x value.
6. Proceeding like this, we will get infinite number of ordered pairs. All those ordered pairs should be included in the set f.
• So we can write: f = {. . . , (-7,-0.143), (-5, -0.2), (1, 1), (2, 0.5), (5, 0.2), (10, 0.1), . . .}
7. The above set f is written in roster form. But we have to remember an important point. It can be written in 3 steps:
(i) Both elements of the ordered pairs are real numbers.
(ii) Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them.
(iii) So it is better to use set builder form to write f.
8. In the set builder form, we can write:
f = {(x,y) : x ∈ R, y = $\mathbf\small{\rm{\frac{1}{x}}}$, $\mathbf\small{\rm{\frac{1}{x}}}$ ∈ R}
• That means:
    ♦ The set f contains all ordered pairs (x,y) such that,
    ♦ x is a real number,
    ♦ y is the reciprocal of x,
    ♦ reciprocal of x is a real number
• But there is a problem. We cannot put x = 0. The function is not defined at x = 0.
• This problem can be solved in 3 steps:
(i) Consider the set R - {0}.
    ♦ Here we are subtracting the 'set containing zero' from the set R
(ii) The resulting set will not contain zero.
    ♦ We must take x only from R - {0}
(iii) So we must modify the above set builder form. We get:
f = {(x,y) : x ∈ R - {0}, y = $\mathbf\small{\rm{\frac{1}{x}}}$, $\mathbf\small{\rm{\frac{1}{x}}}$ ∈ R}
• That means:
    ♦ The set f contains all ordered pairs (x,y) such that,
    ♦ x is an element of R - {0},
    ♦ y is the reciprocal of x,
    ♦ reciprocal of x is a real number
9. Once we write the set f, we can write the domain and range of f.
(i) First we will write the domain:
• Domain of f is the set containing all the first elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of first elements.
• We saw that all the first elements are real numbers (except zero). Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Domain of f = {x : x ∈ R - {0}}
• That means:
    ♦ The domain of f will contain all real numbers except zero.
(ii) Next we will write the range:
• Range of f is the set containing all the second elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of second elements.
• We saw that all the first elements are real numbers (except zero). Since the second elements are reciprocals, they will also be real numbers. So there will be integers, negative values, positive values, fractions, decimals, recurring decimals etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Range of f = {$\mathbf\small{\rm{\frac{1}{x}}}$ : x ∈ R - {0}}
• That means:
    ♦ The range of f will contain reciprocals of all real numbers except zero.
10. We can make a table using the x and y values in the set f. Such a table is convenient to draw the graph of the function.
• Note that, to input for x, we choose convenient numbers from the set R - {0}.
• It is better not to choose numbers with recurring decimals. They will be difficult to plot.

Table 2.6

11. The red curves in fig.2.14(a) below, is the graph of the function.

Fig.2.14

• The graph in fig.b is drawn to a different scale. This can be explained in 5 steps:
(i) The y value is the reciprocal of x value. So we will need many small values on the y axis.
(ii) To achieve this within limited space, we change the scale of the y axis.
(iii) In the fig.2.14(a), we have:
    ♦ Scale of x axis as: 1 cm = 1 unit
    ♦ Scale of y axis as: 1 cm = 1 unit
(iv) In the fig.2.13(b), we have:
    ♦ Scale of x axis as: 1 cm = 1 unit
    ♦ Scale of y axis as: 1 cm = 0.25 unit
(v) So the graph in fig.b is a bit distorted. But the coordinates do not change.
• The reader is advised to prepare a table and draw the graph in his/her own graph books.
• We can write some peculiarities of this red curve. They can be written in 3 steps:
(i) The red curve of f(x) = $\mathbf\small{\rm{\frac{1}{x}}}$ never passes through the origin (0,0)
(ii) Mark any point on the red curve. Note the coordinates of that point.
   ♦ The y coordinate will be the reciprocal of the x coordinate.
   ♦ This is shown in fig.b
   ♦ The green vertical dashed line shows 2
         ✰ The green horizontal dashed line shows the reciprocal 0.5
   ♦ The magenta vertical dashed line shows -5
         ✰ The magenta horizontal dashed line shows the reciprocal -0.2
(iii) We see arrows at both ends of the red curves. There are four arrows. We will call them I, II, III and IV.
I. The top arrow of the right side red curve:
• This arrow indicates that, the curve can go very high up.
• This can be explained as follows:
   ♦ As we move along this curve from right towards the left, x takes values closer and closer to zero.
         ✰ For example, 0.00001 is closer to zero than 0.0001
   ♦ Values closer to zero are very small.
         ✰ The reciprocals of such small values will be very large.
   ♦ The reciprocals are y values.
         ✰ That means y values will be very large.
         ✰ They are very high up in the graph.
         ✰ This arrow indeed indicates that the graph will go very high up (y = +∞).
   ♦ As the x takes values closer and closer to zero, we get the feeling that, this end of the curve is going to touch the y axis.
         ✰ It will touch the y axis when x = 0
         ✰ However, x cannot become equal to zero.
         ✰ If it is zero, then the function can not be defined.
         ✰ This is because, $\mathbf\small{\rm{\frac{1}{x}}}$ becomes $\mathbf\small{\rm{\frac{1}{0}}}$
   ♦ So this end will never touch the y axis
         ✰ When we draw this graph on a sheet of paper or the computer screen, it appears to touch.
         ✰ But if we zoom in, we will see that, there is a little gap.
II. The bottom arrow of the right side red curve:
• This arrow indicates that, the curve can reach to the point where (x = +∞).
• This can be explained as follows:
   ♦ As we move along this curve from left towards the right, x take values closer and closer to +∞.
   ♦ Values closer to +∞ are very large.
         ✰ The reciprocals of such small values will be very small.
   ♦ The reciprocals are y values.
         ✰ That means y values will be very small.
         ✰ They get closer and closer to zero.
   ♦ As the y becomes closer and closer to zero, we get the feeling that, this end of the curve is going to touch the x axis.
         ✰ It will touch the x axis when x = +∞
         ✰ However, x cannot become equal to +∞.
   ♦ So this end will never touch the x axis
         ✰ When we draw this graph on a sheet of paper or the computer screen, it appears to touch.
         ✰ But if we zoom in, we will see that, there is a little gap.
III. The top arrow of the left side red curve:
• This arrow indicates that, the curve can reach to the point where (x = -∞).
• This can be explained as follows:
   ♦ As we move along this curve from right towards the left, x take values closer and closer to -∞.
   ♦ Values closer to -∞ are very large (numerically).
         ✰ The reciprocals of such small values will be very small.
   ♦ The reciprocals are negative y values.
         ✰ That means negative y values will be very small.
         ✰ They get closer and closer to zero.
   ♦ As the y becomes closer and closer to zero, we get the feeling that, this end of the curve is going to touch the x axis.
         ✰ It will touch the x axis when x = -∞
         ✰ However, x cannot become equal to -∞.
   ♦ So this end will never touch the x axis
         ✰ When we draw this graph on a sheet of paper or the computer screen, it appears to touch.
         ✰ But if we zoom in, we will see that, there is a little gap.
IV. The bottom arrow of the left side red curve:
• This arrow indicates that, the curve can go very low bottom.
• This can be explained as follows:
   ♦ As we move along this curve from left towards the right, x takes values closer and closer to zero.
         ✰ For example, -0.0001 is closer to zero than -0.00001
   ♦ Values closer to zero are very small.
         ✰ The reciprocals of such small values will be very large.
   ♦ The reciprocals are negative y values.
         ✰ That means negative y values will be very large (numerically).
         ✰ They are very low down in the graph.
         ✰ This arrow indeed indicates that the graph will go very low bottom (y = -∞).
   ♦ As the x takes values closer and closer to zero, we get the feeling that, this end of the curve is going to touch the y axis.
         ✰ It will touch the y axis when x = 0
         ✰ However, x cannot become equal to zero.
         ✰ If it is zero, then the function can not be defined.
         ✰ This is because, $\mathbf\small{\rm{\frac{1}{x}}}$ becomes $\mathbf\small{\rm{\frac{1}{0}}}$
   ♦ So this end will never touch the y axis
         ✰ When we draw this graph on a sheet of paper or the computer screen, it appears to touch.
         ✰ But if we zoom in, we will see that, there is a little gap.
10. The rational function f(x) = $\mathbf\small{\rm{\frac{1}{x}}}$ has many applications in science and engineering.

---

In the next section, we will see a few more common functions.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 2.3 - Polynomial Function

In the previous section, we saw the basics about functions. We also saw the features of identity function. In this section, we will see constant function and polynomial function.

B. Constant function
This is a real valued function f: R→R defined by y = f (x) = c
Details can be written in 11 steps:
1. Given that, it is a real valued function. That means, all values obtained after processing, must be real values.
• The function can be defined by writing the ordered pairs which satisfy that function.
• So our next task is to find those ordered pairs.
2. It is given that, f : R→R
• This indicates that,
   ♦ the first elements of the ordered pairs (input x values) should be taken from the set R.
   ♦ the second elements (resulting y values) should be present in the set R
3. The set R is the set of real numbers. It will include integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. In short, R will contain every value which can be plotted on a number line. Recall that we plotted √2, √5, π etc., in our previous classes.
• Since different types of numbers are present in R, we will choose some convenient numbers at random.
• Let x = -7
   ♦ This x is processed as follows:
   ♦ f(-7) = c
   ♦ f(-7) is the 'y value' when 'x value' is -7
   ♦ So we get an ordered pair (x,y) as: (-7,c)
• Let x = -3
   ♦ This x is processed as follows:
   ♦ f(-3) = c
   ♦ f(-3) is the 'y value' when 'x value' is -3
   ♦ So we get another ordered pair (x,y) as: (-3,c)
• Let x = 1.414
   ♦ This x is processed as follows:
   ♦ f(1.414) = c
   ♦ f(1.414) is the 'y value' when 'x value' is 1.414
   ♦ So we get another ordered pair (x,y) as: (1.414,c)
• We see that, whatever be the value of x, the value of y will always be c.
4. Proceeding like this, we will get infinite number of ordered pairs. All those ordered pairs should be included in the set f.
• So we can write: f = {. . . , (-7,c), (-3,c), (1.414,c), (5,c), . . .}
5. In step (2), we noted that, the second elements of the ordered pairs must also be from set R.
• Here we have only one second element, which is 'c'.
   ♦ But this 'c' must be from R.
   ♦ That means, 'c' must be a real number.
• Let us put c = 4. Then the function becomes f(x) = 4
• We can write: f = {. . . , (-7,4), (-3,4), (1.414,4), (5,4), . . .}
6. The above set f is written in roster form. But we have to remember an important point. It can be written in 3 steps:
(i) Both elements of the ordered pairs are real numbers.
(ii) Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them.
(iii) So it is better to use set builder form to write f.
7. In the set builder form, we can write:
f = {(x,y) : x ∈ R, y = c, c ∈ R}
• That means:
    ♦ The set f contains all ordered pairs (x,y) such that,
    ♦ x is a real number,
    ♦ y is a constant c,
    ♦ c is a real number
8. Once we write the set f, we can write the domain and range of f.
(i) First we will write the domain:
• Domain of f is the set containing all the first elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of first elements.
• We saw that all the first elements are real numbers. Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Domain of f = {x : x ∈ R}
• That means:
    ♦ The domain of f is the set of all x such that,
    ♦ x is a real number.
(ii) Next we will write the range:
• Range of f is the set containing all the second elements of the ordered pairs in f.
• In our present case, there are infinite number of c. But in a set, we write repeating elements only once.
• We can write:
    ♦ Range of f = {c}
9. We can make a table using the x and y values in the set f. Such a table is convenient to draw the graph of the function.
• Note that, to input for x, we choose convenient numbers from the set R.
• It is better not to choose numbers with recurring decimals. They will be difficult to plot.

Table 2.3

 10. The red line in fig.2.11(a) below, is the graph of this function.

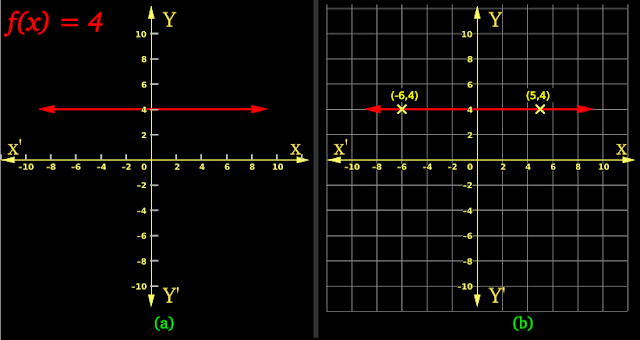Fig.2.11

• The reader is advised to prepare a table and draw the graph in his/her own graph books.
• We can write some peculiarities of this red line. They can be written in 6 steps:
(i) The red line will be always horizontal and passes through y = c
(ii) Mark different points on the red line. Note the coordinates of those points.
   ♦ All y coordinates will be the same c.
   ♦ This is shown in fig.b
(iii) We see arrows at both ends of the red line.
• The arrow at the left end of the red line indicates that, the line can extend up to the point where x = -∞ and y = c.
• The arrow at the right end of the red line indicates that, the line can extend up to the point where x = +∞ and y = c.
11. The constant function has many applications in science and engineering.

C. Polynomial function
• We have seen some basics about polynomials in our earlier classes (Details here).
• A polynomial function is a real valued function f: R→R defined by:
y = f (x) = a₀ + a₁x + a₂x² + a₃x³ + . . . + a_nxⁿ
• Details can be written in 11 steps:
1. Given that, it is a real valued function. That means, all values obtained after processing, must be real values.
• The function can be defined by writing the ordered pairs which satisfy that function.
• So our next task is to find those ordered pairs.
• We will take a simple polynomial function: f(x) = x²
2. It is given that, f : R→R
• This indicates that,
   ♦ the first elements of the ordered pairs (input x values) should be taken from the set R.
   ♦ the second elements (resulting y values) should be present in the set R
3. The set R is the set of real numbers. It will include integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. In short, R will contain every value which can be plotted on a number line. Recall that we plotted √2, √5, π etc., in our previous classes.
• Since different types of numbers are present in R, we will choose some convenient numbers at random.
• Let x = -7
   ♦ This x is processed as follows:
   ♦ f(-7) = (-7)² = 49
   ♦ f(-7) is the 'y value' when 'x value' is -7
   ♦ So we get an ordered pair (x,y) as: (-7,49)
• Let x = -3
   ♦ This x is processed as follows:
   ♦ f(-3) = (-3)² = 9
   ♦ f(-3) is the 'y value' when 'x value' is -3
   ♦ So we get an ordered pair (x,y) as: (-3,9)
• Let x = 1.414
   ♦ This x is processed as follows:
   ♦ f(1.414) = (1.414)² = 2
   ♦ f(1.414) is the 'y value' when 'x value' is 1.414
   ♦ So we get an ordered pair (x,y) as: (1.414,2)
• We see that, whatever be the value of x, the value of y will be the square of that x value.
4. Proceeding like this, we will get infinite number of ordered pairs. All those ordered pairs should be included in the set f.
• So we can write: f = {. . . , (-7,49), (-3,9), (1.414,2), (5,25), . . .}
5. The above set f is written in roster form. But we have to remember an important point. It can be written in 3 steps:
(i) Both elements of the ordered pairs are real numbers.
(ii) Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them.
(iii) So it is better to use set builder form to write f.
6. In the set builder form, we can write:
f = {(x,y) : x ∈ R, y = x², x² ∈ R}
• That means:
    ♦ The set f contains all ordered pairs (x,y) such that,
    ♦ x is a real number,
    ♦ y is the square of x,
    ♦ square of x is a real number
7. Once we write the set f, we can write the domain and range of f.
(i) First we will write the domain:
• Domain of f is the set containing all the first elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of first elements.
• We saw that all the first elements are real numbers. Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Domain of f = {x : x ∈ R}
• That means:
    ♦ The domain of f will contain all real numbers.
(ii) Next we will write the range:
• Range of f is the set containing all the second elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of second elements.
• We saw that all the first elements are real numbers. Since the second elements are squares, there will not be any negative numbers. But there will be integers,  fractions, decimals, recurring decimals etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Range of f = {x² : x ∈ R}
• That means:
    ♦ The domain of f will contain squares of all real numbers.
8. We can make a table using the x and y values in the set f. Such a table is convenient to draw the graph of the function.
• Note that, to input for x, we choose convenient numbers from the set R.
• It is better not to choose numbers with recurring decimals. They will be difficult to plot.

Table 2.4

 9. The red curve in fig.2.12(a) below, is the graph of the function.

Fig.2.12

• The reader is advised to prepare a table and draw the graph in his/her own graph books.
• We can write some peculiarities of this red curve. They can be written in 3 steps:
(i) The red curve of f(x) = x² always passes through the origin (0,0)
(ii) Mark any point on the red curve. Note the coordinates of that point.
   ♦ The y coordinate will be the square of the x coordinate.
   ♦ This is shown in fig.b
   ♦ The green vertical dashed line shows 1.414
         ✰ The green horizontal dashed line shows the square 2
   ♦ The magenta vertical dashed line shows -4
         ✰ The magenta horizontal dashed line shows the square 16
(iii) We see arrows at both ends of the red curve.
• The arrow at the left end of the red curve indicates that, the curve can extend up to the point where x = -∞ and y = square of that x value.
• The arrow at the right end of the red curve indicates that, the curve can extend up to the point where x = +∞ and y = square of that x value.
10. The polynomial function f(x) = x² has many applications in science and engineering.
11. We wrote the general form of polynomial functions as:
y = f (x) = a₀ + a₁x + a₂x² + a₃x³ + . . . + a_nxⁿ
◼ It is important to ensure that:
a₀, a₁, a₂, a₃, . . . , a_n are real numbers
    ♦ In other words, a₀, a₁, a₂, a₃, . . . , a_n ∈ R
◼ It is important to ensure that:
No exponent of x is negative.
◼ It is important to ensure that:
All exponents of x are integers.
[Recall the conditions for a polynomial that we saw in our previous classes. (Details here)]
• Some examples of polynomial functions are:
    ♦ f(x) = x³ – x² + 2
    ♦ g(x) = x⁴ + √2 x
• The following function is not a polynomial function:
    ♦ $\mathbf\small{\rm{h(x)=x^{\frac{2}{3} }+2x}}$
    ♦ This is because, the exponent of x in the first term is not an integer

---

Let us see a solved example:
Solved example 2.28
Draw the graph of the real valued function f :R → R defined by f(x) = x³, x ∈ R.
Solution:
1. Given that, it is a real valued function. That means, all values obtained after processing, must be real values.
• The function can be defined by writing the ordered pairs which satisfy that function.
• So our next task is to find those ordered pairs.
• The given function is: f(x) = x³
2. It is given that, f: R→R
• This indicates that,
   ♦ the first elements of the ordered pairs (input x values) should be taken from the set R.
   ♦ the second elements (resulting y values) should be present in the set R
3. The set R is the set of real numbers. It will include integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. In short, R will contain every value which can be plotted on a number line. Recall that we plotted √2, √5, π etc., in our previous classes.
• Since different types of numbers are present in R, we will choose some convenient numbers at random.
• Let x = -7
   ♦ This x is processed as follows:
   ♦ f(-7) = (-7)³ = -343
   ♦ f(-7) is the 'y value' when 'x value' is -7
   ♦ So we get an ordered pair (x,y) as: (-7, -343)
• Let x = -3
   ♦ This x is processed as follows:
   ♦ f(-3) = (-3)³ = -27
   ♦ f(-3) is the 'y value' when 'x value' is -3
   ♦ So we get an ordered pair (x,y) as: (-3, -27)
• Let x = 1.414
   ♦ This x is processed as follows:
   ♦ f(1.414) = (1.414)³ = 2.8271
   ♦ f(1.414) is the 'y value' when 'x value' is 1.414
   ♦ So we get an ordered pair (x,y) as: (1.414, 2.8271)
(Note that 1.414 is √2. So 2.8271 will be 2√2)
• We see that, whatever be the value of x, the value of y will be the cube of that x value.
4. Proceeding like this, we will get infinite number of ordered pairs. All those ordered pairs should be included in the set f.
• So we can write: f = {. . . , (-7, -343), (-3, -27), (1.414, 2.8271), (5, 125), . . .}
5. The above set f is written in roster form. But we have to remember an important point. It can be written in 3 steps:
(i) Both elements of the ordered pairs are real numbers.
(ii) Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them.
(iii) So it is better to use set builder form to write f.
6. In the set builder form, we can write:
f = {(x,y) : x ∈ R, y = x³, x³ ∈ R}
• That means:
    ♦ The set f contains all ordered pairs (x,y) such that,
    ♦ x is a real number,
    ♦ y is the cube of x,
    ♦ cube of x is a real number.
7. Once we write the set f, we can write the domain and range of f.
(i) First we will write the domain:
• Domain of f is the set containing all the first elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of first elements.
• We saw that all the first elements are real numbers. Since they are real numbers, there will be integers, negative values, positive values, fractions, decimals, recurring decimals, numbers like √2, √5, π etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Domain of f = {x : x ∈ R}
• That means:
    ♦ The domain of f is the set of all x such that,
    ♦ x is a real number.
(ii) Next we will write the range:
• Range of f is the set containing all the second elements of the ordered pairs in f.
• In our present case, there are infinite number of ordered pairs. So there will be infinite number of second elements.
• We saw that all the first elements are real numbers. Since the second elements are cubes, there will be negative numbers also. There will be integers,  fractions, decimals, recurring decimals etc.,. We cannot think of a definite sequence to write them. So it is better to use set builder form rather than the roster form.
• We can write:
    ♦ Range of f = {x³ : x ∈ R}
• That means:
    ♦ The domain of f is the set of all x³ such that,
    ♦ x is a real number.
8. We can make a table using the x and y values in the set f. Such a table is convenient to draw the graph of the function.
• Note that, to input for x, we choose convenient numbers from the set R.
• It is better not to choose numbers with recurring decimals. They will be difficult to plot.

Table 2.5

9. The red curve in fig.2.13(a) below, is the graph of the function.

Fig.2.13

• The graph in fig.b is drawn to a different scale. This can be explained in 5 steps:
(i) The y value is cube of x value. So we will need more values on the y axis.
(ii) To achieve this within limited space, we change the scale of the y axis.
(iii) In the fig.2.13(a), we have:
    ♦ Scale of x axis as: 1 cm = 1 unit
    ♦ Scale of y axis as: 1 cm = 1 unit
(iv) In the fig.2.13(b), we have:
    ♦ Scale of x axis as: 1 cm = 1 unit
    ♦ Scale of y axis as: 1 cm = 10 unit
(v) So the graph in fig.b is a bit distorted. But the coordinates do not change.
• The reader is advised to prepare a table and draw the graph in his/her own graph books.
• We can write some peculiarities of this red curve. They can be written in 3 steps:
(i) The red curve of f(x) = x³ always passes through the origin (0,0)
(ii) Mark any point on the red curve. Note the coordinates of that point.
   ♦ The y coordinate will be the cube of the x coordinate.
   ♦ This is shown in fig.b
   ♦ The green vertical dashed line shows 3
         ✰ The green horizontal dashed line shows the cube 27
   ♦ The magenta vertical dashed line shows -4
         ✰ The magenta horizontal dashed line shows the cube -64
(iii) We see arrows at top and bottom of the red curve.
• The arrow at the top end of the red curve indicates that, the curve can extend up to the point where x = +∞ and y = cube of that x value.
• The arrow at the bottom end of the red curve indicates that, the curve can extend up to the point where x = -∞ and y = cube of that x value.
10. The polynomial function f(x) = x³ has many applications in science and engineering.

---

In the next section, we will see a Rational function.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com