Chapter 1.12 - Practical Problems Involving Three Sets

In the previous section, we saw some interesting relations between three sets. In this section, we will see some practical problems involving three sets.

In a previous section 1.9, we saw the practical problems involving two sets. We saw that some students wanted to be in both cricket team and football team.
We derived Eq.1.1: n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
Using the equation, we solved the situation effectively.

• Now suppose that, a hockey coach also wants to make a team.
   ♦ Some students will want to be in both cricket team and football team.
   ♦ Some students will want to be in both cricket team and hockey team.
   ♦ Some students will want to be in both football team and hockey team.
   ♦ Some students will want to be in all three teams.
• Here also, we can derive an equation similar to the Eq.1.1
   ♦ It can be derived in 7 steps:
1. We want to find n(A ∪ B ∪ C)
• Let us treat B ∪ C as one unit. Then we can write:
n(A ∪ B ∪ C) = n[A ∪ (B ∪ C)]
   ♦ Recall that A ∪ (B ∪ C) = (A ∪ B) ∪ C = A ∪ B ∪ C
   ♦ See figs.1.7 and 1.8 in section 1.5 for proof
2. Now (B ∪ C) occupies a position similar to 'B' in Eq.1.1
• So we can write:
n[A ∪ (B ∪ C)] = n(A) + n(B ∪ C) - n[A ∩ (B ∪ C)]
3. The right side has three terms. We apply Eq.1.1 to the second term. We get:
n[A ∪ (B ∪ C)] = n(A) + n(B) + n(C) - n(B ∩ C) - n[A ∩ (B ∪ C)]
4. Now the right side has 5 terms. We apply the 'distributive law of intersection' to the fifth term.
• Then the fifth term becomes:
n[(A ∩ B) ∪ (A ∩ C)]
5. We apply Eq.1.1 to this modified fifth term. We get:
n[(A ∩ B) ∪ (A ∩ C)] = n(A ∩ B) + n(A ∩ C) - n[(A ∩ B) ∩ (A ∩ C)]
6. The last term on the right side is simply: n(A ∩ B ∩ C)
• So we can write:
n[(A ∩ B) ∪ (A ∩ C)] = n(A ∩ B) + n(A ∩ C) - n(A ∩ B ∩ C)
7. So the fifth term in (3) can be replaced. The modified equation is:
n[A ∪ (B ∪ C)] = n(A) + n(B) + n(C) - n(B ∩ C) - n(A ∩ B) - n(A ∩ C) + n(A ∩ B ∩ C)
• Rearranging this, we get Eq.1.2:
n[A ∪ B ∪ C] = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(A ∩ C) + n(A ∩ B ∩ C)
• There is a definite pattern in this equation:
    ♦ The individual numbers n(A), n(B) and n(C) are added.
    ♦ The intersecting pairs n(A ∩ B), n(B ∩ C) and n(A ∩ C) are subtracted.
    ♦ The overall intersection n(A ∩ B ∩ C) is added.

Let us see a solved example
Solved example 1.69
A college awarded 38 medals in football, 15 in basketball and 20 in cricket. If these medals went to a total of 58 men and only three men got medals in all the three sports, how many received medals in exactly two of the three sports ?
Solution:
1. Given that: n(F) = 38, n(B) = 15 and n(C) = 20
• Also given that: n(F ∪ B ∪ C) = 58 and n(F ∩ B ∩ C) = 3
2. Applying Eq.1.2, we get:
n(F ∪ B ∪ C) = n(F) + n(B) + n(C) - n(F ∩ B) - n(B ∩ C) - n(F ∩ C) + n(F ∩ B ∩ C)
3. Substituting the known values, we get:
58 = 38 + 15 + 20 - n(F ∩ B) - n(B ∩ C) - n(F ∩ C) + 3
⇒ 58 = 76 - n(F ∩ B) - n(B ∩ C) - n(F ∩ C)
⇒ n(F ∩ B) + n(B ∩ C) + n(F ∩ C) = 18
4. The intersection pairs are added three times in the above result in (3)
• That sum in the Venn diagram below is: (a+d) + (b+d) + (c+d)

Fig.1.30

5. We want (a+b+c)
• It can be obtained as:
a+b+c = (a+d) + (b+d) + (c+d) -3d
6. Thus we get:
a+b+c = n(F ∩ B) + n(B ∩ C) + n(F ∩ C) - 3d
⇒ a+b+c = 18 - (3 × 3) = 9

Solved example 1.70
In a survey of 60 people, it was found that 25 people read newspaper H, 26 read
newspaper T, 26 read newspaper I, 9 read both H and I, 11 read both H and T,
8 read both T and I, 3 read all three newspapers. Find:
(i) the number of people who read at least one of the newspapers.
(ii) the number of people who read exactly one newspaper.
Solution:
1. Given that: n(H) = 25, n(T) = 26 and n(I) = 26
• Also given that: n(H ∩ I) = 9, n(H ∩ T) = 11, n(T ∩ I) = 8 and n(H ∩ T ∩ I) = 3
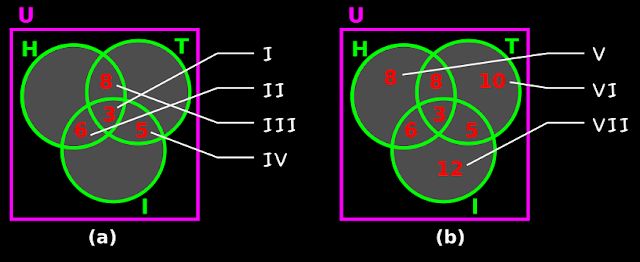
2. This problem can be easily solved using Venn diagrams. The various portions in the Venn Venn diagram can be filled up in 7 steps:
I. Given n(H ∩ T ∩ I) = 3
• So 3 comes in the central portion. This is marked as I in fig.1.31(a) below:

Fig.1.31

II. Given n(H ∩ I) = 9
• So the overlap between H and I is 9
• But 3 is already present in this overlap.
    ♦ So the remaining portion of the overlap is (9 - 3) = 6
• This is marked as II in fig.1.31(a) above. 

III. Given n(H ∩ T) = 11
• So the overlap between H and T is 11
• But 3 is already present in this overlap.
    ♦ So the remaining portion of the overlap is (11 - 3) = 8
• This is marked as III in fig.1.31(a) above. 

IV. Given n(T ∩ I) = 8
• So the overlap between T and I is 8
• But 3 is already present in this overlap.
    ♦ So the remaining portion of the overlap is (8 - 3) = 5
• This is marked as IV in fig.1.31(a) above. 

V. Given n(H) = 25
• So the circle H will enclose 25
• But 8, 3 and 6 are already present inside H.
    ♦ So the extra needed is: [25 - (8+3+6)] = 8
• This is marked as V in fig.1.31(b) above. 

VI. Given n(T) = 26
• So the circle T will enclose 26
• But 8, 3 and 5 are already present inside T.
    ♦ So the extra needed is: [26 - (8+3+5)] = 10
• This is marked as VI in fig.1.31(b) above.  

VII. Given n(I) = 26
• So the circle I will enclose 26
• But 6, 3 and 5 are already present inside I.
    ♦ So the extra needed is: [26 - (6+3+5)] = 12
• This is marked as VII in fig.1.31(b) above.  

3. Now the Venn diagram is completely filled up. We can answer the questions.
(i) the number of people who read at least one of the newspapers.
• The answer will be n(H ∪ T ∪ I)
   ♦ To find this number, we have to add all items inside the three circles.
   ♦ So we get: n(H ∪ T ∪ I)  = (8+8+6+3+10+5+12) = 52
(ii) the number of people who read exactly one newspaper.
• For this, we need to add the non-intersecting portions of the three circles
   ♦ We get: (8+12+10) = 30

Solved example 1.71
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
Solution:
1. Given that: n(A) = 21, n(B) = 26 and n(C) = 29
• Also given that: n(A ∩ B) = 14, n(C ∩ A) = 12, n(B ∩ C) = 14 and n(A ∩ B ∩ C) = 8
2. This problem can be easily solved using Venn diagrams. The various portions in the Venn Venn diagram can be filled up in 7 steps:
I. Given n(A ∩ B ∩ C) = 8
• So 8 comes in the central portion. This is marked as I in fig.1.32(a) below:

Fig.1.32

II. Given n(A ∩ B) = 14
• So the overlap between A and B is 14
• But 8 is already present in this overlap.
    ♦ So the remaining portion of the overlap is (14 - 8) = 6
• This is marked as II in fig.1.32(a) above. 

III. Given n(C ∩ A) = 12
• So the overlap between C and A is 12
• But 8 is already present in this overlap.
    ♦ So the remaining portion of the overlap is (12 - 8) = 4
• This is marked as III in fig.1.32(a) above. 

IV. Given n(B ∩ C) = 14
• So the overlap between B and C is 14
• But 8 is already present in this overlap.
    ♦ So the remaining portion of the overlap is (14 - 8) = 6
• This is marked as IV in fig.1.32(a) above. 

V. Given n(A) = 21
• So the circle A will enclose 21
• But 8, 4 and 6 are already present inside A.
    ♦ So the extra needed is: [21 - (8+4+6)] = 3
• This is marked as V in fig.1.32(b) above. 

VI. Given n(B) = 26
• So the circle B will enclose 26
• But 6, 8 and 6 are already present inside B.
    ♦ So the extra needed is: [26 - (6+8+6)] = 6
• This is marked as VI in fig.1.31(b) above.  

VII. Given n(C) = 29
• So the circle C will enclose 29
• But 4, 8 and 6 are already present inside C.
    ♦ So the extra needed is: [29 - (4+8+6)] = 11
• This is marked as VII in fig.1.32(b) above.  

3. Now the Venn diagram is completely filled up. We can answer the question.
How many like product C only?
• The answer will be the non-intersecting portion of C. It is equal to 11

---

In the next chapter, we will see the Relations and Functions.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 1.11 - Some Interesting Relations Between Three Sets

In the previous section, we saw some interesting relations between two sets. In this section, we will see such relations between three sets. We will see them in the form of solved examples.

Solved example 1.64
Let A, B, and C be the sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C. Show that B = C.
Solution:
• We will solve this problem in two parts (a) and (b).
   ♦ In part (a), we will prove that B ⊂ C
   ♦ In part (b), we will prove that C ⊂ B
Part (a):
1. Let x be an element of B
• Using symbols, we write this as: x ∈ B
2. Then x will be an element of A ∪ B also.
• Using symbols, we write this as: x ∈ B ⇒ x ∈ (A ∪ B)
3. Given that, A ∪ B = A ∪ C
• So x must be an element of A ∪ C also.
• Using symbols, we write this as:
x ∈ (A ∪ B) ⇒ x ∈ (A ∪ C)
4. If x is an element of A ∪ C, it can be an element of A or C
• Using symbols, we write this as:
x ∈ (A ∪ C) ⇒ x ∈ A or x ∈ C
5. Let us assume that, x is an element of A
• In (1), we have already said that x is an element of B
   ♦ So x is an element of both A and B
   ♦ In that case, x will be an element of A ∩ B
• Using symbols, we write this as: x ∈ (A ∩ B)
6. Given that, A ∩ B = A ∩ C
   ♦ So x must be an element of A ∩ C also.
• Using symbols, we write this as:
x ∈ (A ∩ B) ⇒ x ∈ (A ∩ C)
7. If x is an element of A ∩ C, it must be an element of both A and C
• Using symbols, we write this as:
x ∈ (A ∩ C) ⇒ x ∈ A and x ∈ C
• That means, if an element x which belongs to B, is present in A also, it will be present in C also
8. In step (5), instead of assuming A, let us assume that, x belongs to C
• Then we can write:
The element x, which belongs to B, is present in C also
9. So whatever be the assumption that we make in (5), the element x, which belongs to B, will be present in C
◼ Thus we get: B ⊂ C

Part (b):
1. Let y be an element of C
• Using symbols, we write this as: y ∈ C
2. Then y will be an element of A ∪ C also.
• Using symbols, we write this as: y ∈ C ⇒ y ∈ (A ∪ C)
3. Given that, A ∪ B = A ∪ C
• So x must be an element of A ∪ B also.
• Using symbols, we write this as:
y ∈ (A ∪ C) ⇒ y ∈ (A ∪ B)
4. If y is an element of A ∪ B, it can be an element of A or B
• Using symbols, we write this as:
y ∈ (A ∪ B) ⇒ y ∈ A or y ∈ B
5. Let us assume that, y is an element of A
• In (1), we have already said that y is an element of C
   ♦ So y is an element of both A and C
   ♦ In that case, y will be an element of A ∩ C
• Using symbols, we write this as: y ∈ (A ∩ C)
6. Given that, A ∩ B = A ∩ C
   ♦ So y must be an element of A ∩ B also.
• Using symbols, we write this as:
y ∈ (A ∩ C) ⇒ y ∈ (A ∩ B)
7. If y is an element of A ∩ B, it must be an element of both A and B
• Using symbols, we write this as:
y ∈ (A ∩ B) ⇒ y ∈ A and y ∈ B
• That means, if an element y which belongs to C, is present in A also, it will be present in B also
8. In step (5), instead of assuming A, let us assume that, y belongs to B
• Then we can write:
The element y, which belongs to C, is present in B also
9. So whatever be the assumption that we make in (5), the element y, which belongs to C, will be present in B
◼ Thus we get: C ⊂ B

◼ In part (a), we proved: B ⊂ C
◼ In part (b), we proved: C ⊂ B
◼ So we get: B = C

Solved example 1.65
Show that if A ⊂ B, then C – B ⊂ C – A
Solution:
1. Let x be an element of C - B
• Using symbols, we write this as: x ∈ (C - B)
2. C - B will not contain any element of B
• So we can write:
    ♦ x will be an element of C.
    ♦ But x will not be an element of B
• Using symbols, we write this as:
x ∈ (C - B) ⇒ x ∈ C and x ∉ B
3. Given that A is a subset of B
• So all elements of A will be present in B
• In (2), we saw that x is not present in B
    ♦ If x is not present in B, x will not be present in A either.
4. If x is not present in A,
   ♦ x will not be deleted from C when (C - A) is formed
• That means, x will be present in (C - A)
5. So we can write:
x, which is an element of C - B, is an element of C - A also
◼ Thus we get: C - B ⊂ C - A

Solved example 1.66
Show that A ∩ B = A ∩ C need not imply B = C.
Solution:
We can show this using an example. It can be written in 3 steps:
1. Let A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {3, 4, 7, 8}
2. We get: A ∩ B = {3, 4} and A ∩ C = {3, 4}
3. Here A ∩ B = A ∩ C but A ≠ C

Solved example 1.67
Let A and B be sets. If A ∩ X = B ∩ X = ɸ and A ∪ X = B ∪ X for some set X, show that A = B.
(Hints A = A ∩ (A ∪ X), B = B ∩ (B ∪ X) and use Distributive law)
Solution:
• We will solve this problem in two parts (a) and (b)
Part (a):
1. We have: A = A ∩ (A ∪ X)
• (A ∪ X) can be replaced by (B ∪ X) because, it is given that they are equal.
• So we get: A =  A ∩ (B ∪ X)
2. The RHS can be expanded using the distributive law of intersection. We get:
A = (A ∩ B) ∪ (A ∩ X)
⇒ A = (A ∩ B) ∪ ɸ [∵ (A ∩ X) = ɸ]
⇒ A = (A ∩ B)

Part (b):
1. We have: B = B ∩ (B ∪ X)
• (B ∪ X) can be replaced by (A ∪ X) because, it is given that they are equal.
• So we get: B =  B ∩ (A ∪ X)
2. The RHS can be expanded using the distributive law of intersection. We get:
B = (B ∩ A) ∪ (B ∩ X)
⇒ B = (B ∩ A) ∪ ɸ [∵ (B ∩ X) = ɸ]
⇒ B = (A ∩ B)

• From part (a), we have A = (A ∩ B)
• From part (b), we have B = (A ∩ B)
◼ So we can write: A = B

Solved example 1.68
Find sets A, B and C such that A ∩ B, B ∩ C and A ∩ C are non-empty sets and A ∩ B ∩ C = ɸ.
Solution:
1. A ∩ B should be non-empty. That means, there must be at least one common element in A and B.
• So let A = {1, 2} and B = {2, 3}
2. B ∩ C should be non-empty. That means, there must be at least one common element in B and C.
3. A ∩ C should be non-empty. That means, there must be at least one common element in A and C.
• So let C = {1, 3}
4. So we get:
   ♦ A ∩ B = {2}
   ♦ B ∩ C = {3}
   ♦ A ∩ C = {1}
• They are all non-empty sets
5. Now, there is not even a single element which is common in all three sets.
◼ So we get: A ∩ B ∩ C = ɸ.

---

In the next section, we will see the practical problems which involves three sets.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 1.10 - Some Interesting Relations Between Two Sets

In the previous section, we saw some practical problems involving sets. In this section, we will see some interesting relations between sets. We will see them in the form of solved examples.

Solved example 1.56
Show that A ∪ B = A ∩ B implies A = B
Solution:
• We will solve this problem in two parts: Part (a) and Part (b).
    ♦ In part (a), we prove that A ⊂ B
    ♦ In part (b), we prove that B ⊂ A
Part (a):
1. Let a be an element of A.
    ♦ Using symbols, we write this as: a ∈ A
2. Since a is an element of A, the same a will be an element of A ∪ B also.
    ♦ Using symbols, we write this as: a ∈ A ∪ B
3. Given that A ∪ B = A ∩ B
    ♦ So a will be an element of A ∩ B also.
    ♦ Using symbols, we write this as: a ∈ A ∩ B
4. A ∩ B is the set which contains only the common elements of A and B.
    ♦ So, if a is an element of A ∩ B, the same a will be an element of B also.
    ♦ Using symbols, we write this as: a ∈ B
5. Comparing two statements:
    ♦ In (1), we wrote that, a is an element of A.
    ♦ In (4), we saw that, the same a is an element of B also.
• That means, every element in A is an element of B also.
    ♦ Using symbols, we write this as: A ⊂ B

Part (b):
1. Let b be an element of B.
    ♦ Using symbols, we write this as: b ∈ B
2. Since b is an element of B, the same b will be an element of A ∪ B also.
    ♦ Using symbols, we write this as: b ∈ A ∪ B
3. Given that A ∪ B = A ∩ B
    ♦ So b will be an element of A ∩ B also.
    ♦ Using symbols, we write this as: b ∈ A ∩ B
4. A ∩ B is the set which contains only the common elements of A and B.
    ♦ So, if b is an element of A ∩ B, the same b will be an element of A also.
    ♦ Using symbols, we write this as: b ∈ A
5. Comparing two statements:
    ♦ In (1), we wrote that, b is an element of B.
    ♦ In (4), we saw that, the same a is an element of A also.
• That means, every element in B is an element of A also.
    ♦ Using symbols, we write this as: B ⊂ A

◼ In part (a), we proved that, A ⊂ B
◼ In part (b), we proved that, B ⊂ A
◼ This is possible only if the two sets are the same. So we can write: A = B

Solved example 1.57
In each of the following, determine whether the statement is true or false. If it is
true, prove it. If it is false, give an example.
(i) If x ∈ A and A ∈ B , then x ∈ B
(ii) If A ⊂ B and B ∈ C , then A ∈ C
(iii) If A ⊂ B and B ⊂ C , then A ⊂ C
(iv) If A ⊄ B and B ⊄ C , then A ⊄ C
(v) If x ∈ A and A ⊄ B , then x ∈ B
(vi) If A ⊂ B and x ∉ B , then x ∉ A
Solution:
(i) If x ∈ A and A ∈ B , then x ∈ B
This is false. Let us see an example:
• A = {1, 2}, B = {3, {1, 2}, 4}
    ♦ Here A is an element of B.
    ♦ But '1' and '2' are not elements of B.

(ii) If A ⊂ B and B ∈ C , then A ∈ C
This is false. Let us see an example:
A = {1, 2}, B = {1, 2, 3}, C = {4, {1, 2, 3}, 5}
    ♦ Here B is an element of C.
    ♦ But {1, 2} is not an element of C.

(iii) If A ⊂ B and B ⊂ C , then A ⊂ C
This is true. Proof can be written in 3 steps:
1. Let a be an element of A.
    ♦ Using symbols, we write this as: a ∈ A
2. Given that A ⊂ B
    ♦ So all elements of A are present in B.
    ♦ So a ∈ B
3. Given that B ⊂ C
    ♦ So all elements of B are present in C.
    ♦ So a ∈ C
• Thus we get A ⊂ C
◼ The Venn diagram in fig.1.26(a) also proves this.
    ♦ The circle B encloses circle A. This is because A ⊂ B
    ♦ The circle C encloses circle B. This is because B ⊂ A
    ♦ So the circle C automatically encloses circle A, indicating A ⊂ C

Fig.1.26

(iv) If A ⊄ B and B ⊄ C, then A ⊄ C
This is false. Let us see an example:
• A = {1, 2}, B = {2, 3, 4}, C = {1, 2, 3, 5}
    ♦ Here A ⊄ B and B ⊄ C
    ♦ But A ⊂ C
◼ The Venn diagram in fig.1.26(b) also proves that this is false.
   ♦ The circle B does not enclose circle A because A ⊄ B
   ♦ The circle C does not enclose circle B because B ⊄ C
   ♦ But the circle C can enclose circle A because A ⊂ C

(v) If x ∈ A and A ⊄ B , then x ∈ B
This is false. It can be written in steps:
1. Given that x is an element of A.
2. Given that A is not a subset of B. So all elements of A are not present in B.
3. So x need not be present in B.
Let us see an example:
• A = {1, 2}, B = {2, 3, 4}
    ♦ Here A ⊄ B
    ♦ Also, '1' is not present in B.

(vi) If A ⊂ B and x ∉ B , then x ∉ A.
This is true. It can be proved in 2 steps:
1. Given that A is a subset of B. So all elements of A will be present in B.
2. So if x is not present in B, it cannot be present in A.

Solved example 1.58
Show that the following four conditions are equivalent :
(i) A ⊂ B  (ii) A – B = ɸ  (iii) A ∪ B = B  (iv) A ∩ B = A
Solution:
Part (a):
• In this part, we prove that: A ⊂ B  ⇒ A – B = ɸ
   ♦ It can be proved in 4 steps:
1. To find A - B, we first discard all elements of B.
2. Then we discard elements which are common in both A and B.
3. But when we discard the elements in B, we automatically discard the following two items:
   ♦ Common elements mentioned in (2).
   ♦ All elements of A.
4. So after the operation A - B, none of the elements of either A or B will remain.
• So we can write:
If A ⊂ B, the difference A - B will be a null set.
• In other words, A ⊂ B  ⇒ A – B = ɸ

Part (b):
• In this part, we prove that: A ⊂ B ⇒ A ∪ B = B
   ♦ It can be proved in 4 steps:
1. To find A ∪ B, we write all elements of A and B together, but repeating elements will be written only once.
2. Here, all elements of A will be repeating. So none of the elements of A need to be considered.
3. All we need to do is: Write the elements of B.
4. So we can write: A ⊂ B ⇒ A ∪ B = B

Part (c):
In this part, we prove that: A ⊂ B ⇒ A ∩ B = A
   ♦ It can be proved in 4 steps:
1. To find A ∩ B, we write all elements which are common to both A and B.
2. Here, all elements of A are the common elements. In fact, they are the only common elements.
3. All we need to do is: Write the elements of A.
4. So we can write: A ⊂ B ⇒ A ∩ B = A

◼ Thus we see that, all given conditions are equivalent.

Solved example 1.59
Assume that P(A) = P(B). Show that A = B
Solution:
• We will solve this problem in two parts: Part (a) and Part (b).
    ♦ In part (a), we prove that A ⊂ B
    ♦ In part (b), we prove that B ⊂ A
Part (a):
1. P(A) will contain all subsets of A.
• So P(A) will contain A.
• Using symbols, we write this as: A ∈ P(A)
2. If A is an element of P(A), the same A will be an element of P(B) also.
   ♦ Because, it is given that P(A) = P(B)
• Using symbols, we write this as:
A ∈ P(A) ⇒ A ∈ P(B) [∵ P(A) = P(B)]
3. If A is an element of P(B), A will be a subset of B.
• Using symbols, we write this as: A ∈ P(B) ⇒ A ⊂ B
◼ Thus we proved that A ⊂ B

Part (b):
1. P(B) will contain all subsets of B.
• So P(B) will contain B.
• Using symbols, we write this as: B ∈ P(B)
2. If B is an element of P(B), the same B will be an element of P(A) also.
   ♦ Because, it is given that P(A) = P(B)
• Using symbols, we write this as:
B ∈ P(B) ⇒ B ∈ P(A) [∵ P(A) = P(B)]
3. If B is an element of P(A), B will be a subset of A.
• Using symbols, we write this as: B ∈ P(A) ⇒ B ⊂ A
◼ Thus we proved that B ⊂ A

• So we get: A ⊂ B and B ⊂ A
   ♦ This is possible only if A and B are equal.
◼  That means, A = B

Solved example 1.60
Is it true that for any sets A and B, P(A) ∪ P(B) = P(A ∪ B)? Justify your answer.
Solution:
This is false. Let us see an example. It can be written in steps:
1. Let A = {1, 2} and B = {2, 3}
• Then the power sets are:
   ♦ P(A) = {{1}, {2}, {1, 2}, ɸ}
   ♦ P(B) = {{2}, {3}, {2, 3}, ɸ}
2. So P(A) ∪ P(B) will be: {{1}, {2}, {3}, {1, 2}, {2, 3}, ɸ}
3. (A ∪ B) will be: {1, 2, 3}
• Then the power set of (A ∪ B) will be:
P(A ∪ B) = {{1}, {2}, {3}, {1, 2, 3}, {1, 2}, {2, 3}, {1, 3}, ɸ}
4. We see that, result in (2) is different from result in (3).

Solved example 1.61
Show that for any sets A and B,
A - B = A ∩ B'
Solution:
1. Consider the LHS: A - B
   ♦ To find A - B, we discard all elements of B.
   ♦ Then we discard those elements of A which are present in B also.
• The result will be the left side crescent in fig.1.27(b) below:

Fig.1.27

(The dotted B circle is imaginary. It does not come in the result. It is shown only to indicate relative positions)
2. Consider the RHS A ∩ B'
• B' is shown in fig.1.28(a) below. It is the red shaded portion.

Fig.1.28

• We want the intersection of two regions:
   ♦ Region B'
   ♦ Region A
3. The resulting intersection is the region,
   ♦ Where there is shading from both regions B' and A.
• So the result will be as in fig.1.28(b)
4. We see that:
Fig.1.27(b) is same as fig.1.28(b)
◼ So we can write: A - B = A ∩ B'
◼ Similarly, we can prove that: B - A = B ∩ A'

Solved example 1.62
Show that for any sets A and B,
(a) A = (A ∩ B) ∪ (A – B)
(b) A ∪ (B – A) = (A ∪ B)
Solution:
Part (a):
1. We have to prove that A = (A ∩ B) ∪ (A – B)
• Consider (A - B) in the RHS
• From the results in the previous solved example 1.61, we can write (A ∩ B') in the place of (A - B)
2. So the RHS becomes:
(A ∩ B) ∪ (A ∩ B')
3. Now recall the distributive law of intersection (Fig.1.14 of section 1.6):
X ∩ (Y ∪ Z) = (X ∩ Y) ∪ (X ∩ Z)
• The RHS in this law is similar to the result written in (2)
• So the result in (2) becomes: A ∩ (B ∪ B')
4. So the question becomes:
Prove: A = A ∩ (B ∪ B')
5. Consider (B ∪ B') in the RHS
• (B ∪ B') is U
• So the RHS in (4) becomes: A ∩ U
6. But A ∩ U is A
• So LHS and RHS are equal.

Part (b):
1. We have to prove that A ∪ (B – A) = (A ∪ B)
• Consider (B - A) in the LHS.
• From the results in the previous solved example 1.61, we can write (B ∩ A') in the place of (B - A)
2. So the LHS becomes:
A ∪ (B ∩ A')
3. Now recall the distributive law of union:
X ∪ (Y ∩ Z) = (X ∪ Y) ∩ (X ∪ Z)
• The LHS in this law is similar to the result written in (2)
• So the result in (2) becomes: (A ∪ B) ∩ (A ∪ A')
4. So the question becomes:
Prove: (A ∪ B) ∩ (A ∪ A') = (A ∪ B)
5. Consider (A ∪ A') in the RHS
• (A ∪ A') is U
• So the LHS in (4) becomes: (A ∪ B) ∩ U
6. But (A ∪ B) ∩ U is (A ∪ B)
• So LHS and RHS are equal.

Alternate method using Venn diagrams:
1. Fig.1.29(a) below shows our familiar 'Venn diagram of two sets'.

Fig.1.29

2. Fig.1.29(b) shows the three portions separated from each other. This is also familiar to us.
◼ It is clear that, the union of
    ♦ left crescent portion
    ♦ and the middle portion
    ♦ will give set A 
• This proves part (a): A = (A ∩ B) ∪ (A – B)
3. From part (a), we have: A = (A ∩ B) ∪ (A – B)
• So A ∪ (B – A) = (A ∪ B) is same as: (A ∩ B) ∪ (A – B) ∪ (B – A)
    ♦ This is the union of the three portions in fig.1.29(b)
• The union of those three portions will give (A ∪ B)
• This proves part (b): A ∪ (B – A) = (A ∪ B)   

Solved example 1.63
Using properties of sets, show that
(a) A ∪ ( A ∩ B ) = A
(b) A ∩ ( A ∪ B ) = A.
Solution:
Part (a):
1. We have to prove that A ∪ ( A ∩ B ) = A
• Consider the LHS. Recall the distributive law of union:
X ∪ (Y ∩ Z) = (X ∪ Y) ∩ (X ∪ Z)
2. Applying this law, the LHS becomes:
(A ∪ A) ∩ (A ∪ B)
3. But (A ∪ A) is A
• So the LHS becomes:
A ∩ (A∪B)
4. But A ∩ (A∪B) is A
• So the LHS becomes A
5. Thus we get LHS = RHS

Part (b):
1. We have to prove that A ∩ ( A ∪ B ) = A
• Consider the LHS. Recall the distributive law of intersection (Fig.1.14 of section 1.6):
X ∩ (Y ∪ Z) = (X ∩ Y) ∪ (X ∩ Z)
2. Applying this law, the LHS becomes:
(A ∩ A) ∪ (A ∩ B)
3. But (A ∩ A) is A
• So the LHS becomes:
A ∪ (A ∩ B)
4. But in part (a), we proved that A ∪ (A ∩ B) is A.
• So the LHS becomes A.
5. Thus we get LHS = RHS

---

In the next section, we will see some relations between three sets.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 1.9 - Practical Problems Involving Two Sets

In the previous section, we saw complement of sets. In this section, we will see some practical problems involving sets.

• First we will see those problems which involve two sets. In later sections, we will see problems which involve three sets.
• When only two sets are involved, some basics can be written using an example. It can be written in 7 steps:
1. The cricket coach wants to make a team of cricket players. He approaches a class of 35 students and interviews each of them. He finds that, 24 students like to play cricket.
2. After a few days, the football coach approaches the same class. He wants to make a football team. He finds that, 16 students like to play football.
3. The next day, the two coaches have a chat.
• The cricket coach says:
24 students like to play cricket. I can make a cricket team by picking the best among them.
• The football coach says:
16 students like to play football. I can make a football team by picking the best among them.
4. But now a problem arises:
   ♦ (24 + 16) is 40
   ♦ The strength of the class is only 35
• How is that possible?
5. We can solve this problem by using set theory. It can be written in 7 steps:
(i) The Venn diagram in fig.1.24(a) below shows two sets:

Fig.1.24

• All the names in the list possessed by the cricket coach are written inside the C circle.
• All the names in the list possessed by the football coach are written inside the F circle.
(ii) But some names appear in both the circles. If we count the total number, we will get (24 + 16) = 40.
• We know that, inside U, elements must appear only once. So we modify the diagram as shown in fig.b
(iii) Now the total number becomes 35.
• It is clear that, the total number of 40 was wrongly calculated because, some students wanted to be in both teams.
(iv) The modified Venn diagram in fig.b is split into three disjoint sets. This is shown in fig.c
• From the Venn diagram in fig.c, three points become clear. They are numbered as (a), (b) and (c):
(a) The number of students who like to play both games is:
    ♦ The number of elements in the set C ∩ F
    ♦ This is equal to: n(C ∩ F)
(b) The number of students who like to play cricket only is:
    ♦ The number of elements in the set [C – (C ∩ F)]
    ♦ This is equal to: n(C) - n(C ∩ F)
(c) The number of students who like to play football only is:
    ♦ The number of elements in the set [F – (C ∩ F)]
    ♦ This is equal to: n(F) - n(C ∩ F)
(v) Now we can equate the numbers:
   ♦ The number of elements in the union (C ∪ F)
   ♦ must be equal to
   ♦ The total number of elements in the three disjoint sets.
(vi) Thus we get:
n(C ∪ F) = n(C) - n(C ∩ F) + n(C ∩ F) + n(F) - n(C ∩ F)
⇒ n(C ∪ F) = n(C) + n(F) - n(C ∩ F)
(vii) Substituting the known values, we get:
35 = 24 + 16 -  n(C ∩ F)
⇒ n(C ∩ F) = 5
• That mean, 5 students like to be in both the teams.
6. The equation in 5(vi) above can be written in a general form:
Eq.1.1: n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
• There are four quantities in this equation. If any three is known, the unknown quantity can be easily calculated.
7. An important point can be written in 2 steps:
(i) In this problem, every student wants to play.
◼ This fact is written as:
Each student likes to play at least one of the two games.
(ii) If one or more students do not want to be part of any team, the Eq.1.1 will not work.
   ♦ In such cases, we will have to use complement sets.
   ♦ We will see such problems later.

---

Let us see another example:
In a school there are 20 teachers who teach mathematics or physics. Of
these, 12 teach mathematics and 4 teach both physics and mathematics. Every teacher can teach at least one of the two subjects. How many teach physics ?
Solution:
1. Naming of sets:
• Let M denote the set of teachers who can teach mathematics
   ♦ So M will contain the names of all teachers who can teach mathematics
• Let P denote the set of teachers who can teach physics
   ♦ So P will contain the names of all teachers who can teach physics
2. The set (M ∩ P) will contain the names of those teachers who are able to teach both subjects
3. Applying Eq.1.1, we get:
n(M ∪ P) = n(M) + n(P) - n(M ∩ P)
• Substituting the known values, we get:
20 = 12 + n(P) - 4
⇒ n(P) = 12
4. So we can write: 12 teachers can teach physics only.

---

Another example:
If X and Y are two sets such that X ∪ Y has 50 elements, X has 28 elements and Y has 32 elements, how many elements does X ∩ Y have ?
Solution:
1. Applying Eq.1.1, we get:
n(X ∪ Y) = n(X) + n(Y) - n(X ∩ Y)
• Substituting the known values, we get:
50 = 28 + 32 - n(X ∩ Y)
⇒ n(X ∩ Y) = 10

---

Another example:
There are 200 individuals with a skin disorder, 120 had been exposed to the chemical C₁, 50 to chemical C₂ and 30 to both the chemicals C₁ and C₂. Every individual has been exposed to at least one chemical. Find the number of individuals exposed to
(i) Chemical C₁ but not chemical C₂
(ii) Chemical C₂ but not chemical C₁
(iii) Chemical C₁ or chemical C₂
Solution:
1. Tests conducted by three agencies:
• An agency conducts tests on people in a locality.
   ♦ They want to find the number of people exposed to chemical C₁.
   ♦ They find the presence of C₁ in 120 individuals.
   ♦ The set C₁ prepared by this agency, contains those 120 names.
• A second agency conducts tests on people in that locality.
   ♦ They want to find the number of people exposed to chemical C₂.
   ♦ They find the presence of C₂ in 50 individuals.
   ♦ The set C₂ prepared by this agency, contains those 50 names.
• A third agency conducts tests on people in that locality.
   ♦ They want to find the number of people exposed to both C₁ and C₂.
   ♦ They find the presence of both C₁ and C₂ in 30 individuals.
• Adding the numbers in the three sets, we get: (120 + 50 + 30) = 200
2. But it is clear that, the set C₁ will contain the names in the third set also.
• So the number of individuals exposed to C₁ only is (120 - 30) = 90
• This number is in fact [n(C₁) - n(C₁ ∩ C₁)].
• This is the number of elements in the left side crescent in fig.1.25(b) below.
• So the answer to the first part is 90

Fig.1.25

3. In a similar way, the set C₂ will contain the names in the third set also.
• So the number of individuals exposed to C₂ only is (50 - 30) = 20
• This number is in fact [n(C₂) - n(C₁ ∩ C₂)].
• This is the number of elements in the right side crescent in fig.1.25(b).
• So the answer to the second part is 20.
4. In the third part, the word 'or' is present. This indicates union.
• The union must include three items:
   ♦ Those exposed to C₁ only.
   ♦ Those exposed to both C₁ and C₂.
   ♦ Those exposed to C₂ only.
• It is the union of the three portions in fig.1.25(b)
• So the answer to the third part is (90 + 30 + 20) = 140
   ♦ This is a direct application of Eq.1.1
   ♦ The only unknown is n(A ∪ B)

---

The link below gives some solved examples:

Solved examples 1.45 to 1.55

---

Now we will see a practical problem which involves two sets and complement sets.

In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple as well as orange juice. Find how many students were taking neither apple juice nor orange juice.
Solution:
1. Naming of sets:
• Let U denote the set of all 400 students in the school.
   ♦ So U will contain the names of all the 400 students in the school.
• Let A denote the set of students who like apple juice.
   ♦ So A will contain the names of all students who like apple juice.
• Let O denote the set of students who like orange juice.
   ♦ So O will contain the names of all students who like orange juice.
2. The set (A ∩ O) will contain the names of those students who like both apple juice and orange juice.
3. Applying Eq.1.1, we get:
n(A ∪ O) = n(A) + n(O) - n(A ∩ O)
• Substituting the known values, we get:
n(A ∪ O) = 100 + 150 - 75
⇒ n(A ∪ O) = 175
4. A ∪ O is a union. It contains the name of all the students who like at least one juice.
• So the set which contains the names of all the students who like neither apple juice nor orange juice will be (A ∪ O)'
• This complement set will be same as: [U - (A ∪ O)]
• Number of elements in this complement set can be calculated as:
n(U) - n(A ∪ O) = (400 - 175) = 225

Another example:
In a survey of 600 students in a school, 150 students were found to be taking tea
and 225 taking coffee, 100 were taking both tea and coffee. Find how many
students were taking neither tea nor coffee?
Solution:
1. Naming of sets:
• Let U denote the set of all 600 students in the school.
   ♦ So U will contain the names of all the 600 students in the school.
• Let T denote the set of students who like tea.
   ♦ So T will contain the names of all students who like tea.
• Let C denote the set of students who like coffee.
   ♦ So C will contain the names of all students who like coffee.
2. The set (T ∩ C) will contain the names of those students who like both tea and coffee.
3. Applying Eq.1.1, we get:
n(T ∪ C) = n(T) + n(C) - n(T ∩ C)
• Substituting the known values, we get:
n(T ∪ C) = 150 + 225 - 100
⇒ n(T ∪ C) = 275
4. T ∪ C is a union. It contains the name of all the students who like at least one drink.
• So the set which contains the names of all the students who like neither tea nor coffee will be (T ∪ C)'
• This complement set will be same as: [U - (T ∪ C)]
• Number of elements in this complement set can be calculated as:
n(U) - n(T ∪ C) = (600 - 275) = 325

---

In the next section, we will see some interesting relations between sets. After that, we will see the practical problems which involves three sets.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com