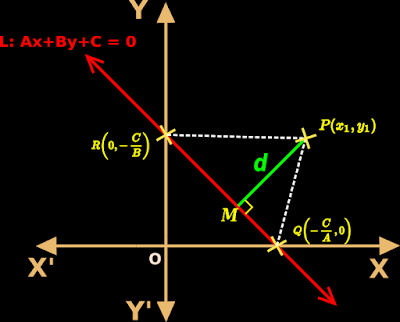
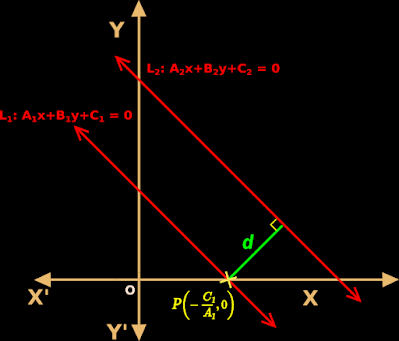
In the previous section, we saw the distance of a point from a line. In this section, we will see some miscellaneous examples.
Solved example 10.20
If the lines 2x+y-3=0, 5x+ky-3=0 and 3x-y-2=0 are concurrent, find the value of k.
Solution:
1. Three lines are said to be concurrent if all three of them pass through a common point.
• In such a situation,
♦ We can consider the point of intersection of any two of those lines.
♦ Let this point of intersection be P.
♦ Then the third line will also pass through P.
2. In our present case,
♦ The first and third lines do not have any unknown quantities.
♦ The second line has an unknown quantity 'k'.
• So we will solve the first and third equations. The solution will give the point of intersection of the first and third lines.
3. We first multiply (I) by 3. We get: 6x+3y-9=0 - - - (IV)
• Then we multiply (III) by 2. We get: 6x-2y-4=0 - - - (V)
• Subtracting (V) from (IV), we get: y = 1
• Substituting y = 1 in (I), we get: x = 1
4. So the point of intersection of (I) and (III) is (1,1)
5. Line (II) also passes through (1,1).
• So we can write: 5 × 1 + k × 1 - 3 = 0
• From this we get: k = -2
6. The actual plot is shown in fig.10.42 below:
 |
| Fig.10.42 |
Solved example 10.21
Find the distance of the line 4x-y=0 from the point P(4,1) measured along the line making an angle of 135o with the +ve x-axis.
Solution:
1. Consider a line which makes 135o with the +ve side of the x-axis.
• We can draw infinite number of such lines. But only one of them will pass through the point P(4,1). This line is shown in red color in the rough sketch below:
 |
| Fig.10.43 Rough sketch |
2. The given line 4x-y=0 is shown in yellow color.
• Consider this line 4x-y=0
♦ Here, A = 4, B = -1 and C = 0
♦ So slope = -A/B = 4
✰ Since slope is +ve, the line has an upward slope
✰ Since C = 0, the line passes through the origin
• Even when we draw rough sketches, it is better to take care of such details.
3. Any two non-parallel lines will intersect at a point.
• In our case, the red and yellow lines intersect at Q.
4. We are required to find the length PQ.
5. For that, first we find the equation of the red line.
• The slope of the red line will be tan 135o = -1
• So we have the slope of the red line. We also have a point on the red line. We can use the point-slope form:
$\begin{array}{ll}
{}&{y-y_0}
&{}={}& {m(x-x_0)}
&{} \\
{\Rightarrow}&{y-1}
&{}={}&
{-1(x-4)}
&{} \\
{\Rightarrow}&{y-1}
&{}={}&
{-x+4}
&{} \\
{\Rightarrow}&{x+y-5}
&{}={}&
{0}
&{} \\
\end{array}$
6. Point Q can be determined by solving the equations of the two lines:
4x-y=0 - - - (I)
x+y-5=0 - - - (II)
7. Solving the two equations, we get: x = 1 and y = 4
• So the coordinates of Q are (1,4)
8, Now we have the coordinates of both P and Q.
♦ Coordinates of P are (4,1)
♦ Coordinates of Q are (1,4)
• We can use the distance formula:
$\begin{array}{ll}
{}&{d}
&{}={}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{(1 - 4)^2~+~(4 - 1)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{(- 3)^2~+~(3)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{9~+~9}}
&{} \\
{}&{}
&{}={}& {\sqrt{18}}
&{} \\
{}&{}
&{}={}& {3\sqrt{2}~=~4.24~\text{units}}
&{} \\
\end{array}$
9. The actual plot is shown below:
 |
| Fig.10.44 |
Solved example 10.22
Assuming that straight lines work as the plane mirror for a point, find the image of the point (1,2) in the line x-3y+4=0
Solution:
1. In the rough sketch below, the line x-3y+4=0 is shown in red color. This line is to be considered as the mirror line.
• We want the image of the point P(1,2)
 |
| Fig.10.45 Rough sketch |
2. Let Q(h,k) be the image of P.
• Then PQ will be perpendicular to the mirror line. Using this property, we can find the equation of PQ:
(i) For the mirror line, A = 1, B = -3 and C = 4
• So slope = -A/B = 1/3
• Then slope of the perpendicular line PQ = -3
(ii) We have the point P(1,2) and the slope of PQ. So we can use the point-slope form:
$\begin{array}{ll}
{}&{y-y_0}
&{}={}& {m(x-x_0)}
&{} \\
{\Rightarrow}&{y-2}
&{}={}&
{-3(x-1)}
&{} \\
{\Rightarrow}&{y-2}
&{}={}&
{-3x+3}
&{} \\
{\Rightarrow}&{3x+y-5}
&{}={}&
{0}
&{} \\
\end{array}$
3. Let PQ intersect the mirror line at R.
• We can find the coordinates of R by solving the two equations:
x-3y+4=0 - - - (I)
♦ This is the equation of the mirror line.
3x+y-5=0 - - - (II)
♦ This is the equation of PQ
• Solving the two equations, we get: x = 11/10 and y = 17/10
• So the coordinates of R are (11/10, 17/10)
4. Since Q(h,k) is the image of P(1,2), the point R will be the midpoint of PQ.
We can find the coordinates of the midpoint as follows:
$\begin{array}{ll}
{}&{\text{Midpoint}}
&{}={}& {\left( \frac{x_1 + x_2}{2},\frac{y_1 + y_2}{2} \right)}
&{} \\
{}&{}
&{}={}& {\left( \frac{1 + h}{2},\frac{2 + k}{2} \right)}
&{} \\
\end{array}$
5. Using the results in (3) and (4), we can write:
(i) (1+h)/2 = 11/10
♦ So h = 6/5
(ii) (2+k)/2 = 17/10
♦ So k = 7/5
6. So the image of P(1,2) is Q(6/5, 7/5) = Q(1.2, 1.4)
• The actual plot is shown below:
 |
| Fig.10.46 |
Solved example 10.23
Show that the area of the triangle formed by the lines y= m1x+c1, y=m2x+c2 and x = 0 is $\frac{\left(c_1 - c_2 \right)^2}{2|m_1 - m_2|}$
Solution:
1. The equation x=0 is the equation of the y-axis.
• So the triangle is formed between the two lines and the y-axis. This is shown in the rough sketch below:
 |
| Fig.10.47 Rough sketch |
• The line y= m1x+c1 is shown in green color. It intersects the y-axis at P.
• The line y= m2x+c2 is shown in red color. It intersects the y-axis at Q.
• The two lines intersect at R.
• We need to find the area of the triangle PQR.
2. The given lines are in slope-intercept form. So we can easily write the intercepts that the lines make with the y-axis.
• We can write:
♦ The y-intercept of the line y= m1x+c1 is c1. So the coordinates of P are (0,c1)
♦ The y-intercept of the line y= m2x+c2 is c2. So the coordinates of Q are (0,c2)
3. Our next task is to find the coordinates of R. This can be done by solving the two equations. It is shown below:
$\begin{array}{ll}
{}&{m_1 x}
& {~-~y}& {~=~}
&{~-~}&{c_1}&{\color{green}{\text{ - - - (I)}}} \\
{}&{m_2 x}
& {~-~y}& {~=~}
&{~-~}&{c_2}&{\color{green}{\text{ - - - (II)}}} \\
{}&{m_1 x - m_2 x}
& {~-~y + y}& {~=~}
&{~-~}&{c_1 + c_2}&{\color{green}{\text{ - - - I - II}}} \\
{\Rightarrow}&{(m_1 - m_2) x}
& {~-~0}& {~=~}
&{~-~}&{c_1 + c_2}&{} \\
{\Rightarrow}&{}
& {x}& {~=~}
&{}&{\frac{c_2 - c_1}{m_1 - m_2}}&{} \\
{}&{m_1 \times \frac{c_2 - c_1}{m_1 - m_2}}
& {~-~y}& {~=~}
&{~-~}&{c_1}&{\color{green}{\text{substituting for x in I}}} \\
{\Rightarrow}&{}
& {~-~y}& {~=~}
&{~-~}&{c_1~-~m_1 \times \frac{c_2 - c_1}{m_1 - m_2}}&{} \\
{\Rightarrow}&{}
& {~+~y}& {~=~}
&{~+~}&{C_1~+~m_1 \times \frac{c_2 - c_1}{m_1 - m_2}}&{} \\
{\Rightarrow}&{}
& {y}& {~=~}
&{}&{\frac{c_1(m_1 - m_2)~+~m_1(c_2 - c_1)}{m_1 - m_2}}&{} \\
{\Rightarrow}&{}
& {y}& {~=~}
&{}&{\frac{c_1 m_1 - c_1 m_2~+~m_1 c_2 - m_1 c_1}{m_1 - m_2}}&{} \\
{\Rightarrow}&{}
& {y}& {~=~}
&{}&{\frac{m_1 c_2~-~c_1 m_2}{m_1 - m_2}}&{} \\
{\Rightarrow}&{}
& {y}& {~=~}
&{}&{\frac{m_1 c_2~-~m_2 c_1}{m_1 - m_2}}&{} \\
\end{array}$
• Thus we get the coordinates of R: $\left(\frac{c_2 - c_1}{m_1 - m_2},~\frac{m_1 c_2~-~m_2 c_1}{m_1 - m_2} \right)$
4. So the vertices of the triangle are:
• $P (0,~c_1)$
• $Q (0,~c_2)$
• $R \left(\frac{c_2 - c_1}{m_1 - m_2},~\frac{m_1 c_2~-~m_2 c_1}{m_1 - m_2} \right)$
5. Now we can find the area of the triangle:
$\begin{array}{ll}
{}&{\text{Area}}
&{}={}& {\frac{1}{2} \left|x_1(y_3 - y_2)~+~x_2(y_1 - y_3)~+~x_3(y_2 - y_1) \right|}
&{} \\
{}&{}
&{}={}& {\frac{1}{2} \left|0 \times (y_3 - y_2)~+~0 \times (y_1 - y_3)~+~x_3(y_2 - y_1) \right|}
&{} \\
{}&{}
&{}={}& {\frac{1}{2} \left|x_3(y_2 - y_1) \right|}
&{} \\
{}&{}
&{}={}& {\frac{1}{2} \left|\frac{c_2 - c_1}{m_1 - m_2} \times (c_2 - c_1) \right|}
&{} \\
{}&{}
&{}={}& {\frac{1}{2} \left|\frac{(c_2 - c_1)^2}{m_1 - m_2} \right|}
&{} \\
{}&{}
&{}={}& {\frac{(c_2 - c_1)^2}{\left|2(m_1 - m_2) \right|}}
&{} \\
\end{array}$
Solved example 10.24
A line is such that it's segment between the lines 5x-y+4=0 and 3x+4y-4=0 is bisected at the point (1,5). Obtain it's equation.
Solution:
1. Consider the rough sketch below:
 |
| Fig.10.48 Rough sketch |
• The given lines are shown in red and green colors.
♦ The red line 5x-y+4=0 intersects the yellow line at P
♦ The green line 3x+4y-4=0 intersects the yellow line at Q
• Midpoint of PQ is R(1,5)
• We are asked to find the equation of the yellow line.
2. Let 'm' be the slope of the yellow line.
• The yellow line passes through (1,5)
• So the equation of the yellow line will be y-5 = m(x-1)
• This is same as y-5 = mx - m
• This is same as mx - y = m - 5
3. The coordinates of P can be calculated by solving the equations of the red line and the yellow line.
$\begin{array}{ll}
{}&{m x}
&{~-~}& {y}& {~=~}
&{m-5}&{}&{}&{\color{green}{\text{ - - - (I)}}} \\
{}&{5 x}
&{~-~}& {y}& {~=~}
&{-4}&{}&{}&{\color{green}{\text{ - - - (II)}}} \\
{}&{mx - 5 x}
&{~-~}& {y + y}& {~=~}
&{m - 5 + 4}&{}&{}&{\color{green}{\text{ - - - (I) - (II)}}} \\
{\Rightarrow}&{mx - 5 x}
&{~-~}& {0}& {~=~}
&{m - 1}&{}&{}&{} \\
{\Rightarrow}&{(m - 5) x}
&{}& {}& {~=~}
&{m - 1}&{}&{}&{} \\
{\Rightarrow}&{x}
&{}& {}& {~=~}
&{\frac{m-1}{m-5}}&{}&{}&{} \\
\end{array}$
• We can write: x coordinate of P is: $\frac{m-1}{m-5}$
• In this problem, we do not need to find the y coordinate of P.
4. The coordinates of Q can be calculated by solving the equations of the green line and the yellow line.
$\begin{array}{ll}
{}&{m x}
&{~-~}& {y}& {~=~}
&{m-5}&{}&{}&{\color{green}{\text{ - - - (I)}}} \\
{}&{3x}
&{~+~}& {4y}& {~=~}
&{4}&{}&{}&{\color{green}{\text{ - - - (II)}}} \\
{}&{4mx}
&{~-~}& {4y}& {~=~}
&{4m - 20}&{}&{}&{\color{green}{\text{ - - - [(I) × 4] - - -(III)}}} \\
{}&{4mx + 3x}
&{~-~}& {4y + 4y}& {~=~}
&{4m - 20 + 4}&{}&{}&{\color{green}{\text{ - - - (III) + (II)}}} \\
{\Rightarrow}&{4mx + 3x}
&{~-~}& {0}& {~=~}
&{4m - 16}&{}&{}&{} \\
{\Rightarrow}&{(4m + 3) x}
&{}& {}& {~=~}
&{4m - 16}&{}&{}&{} \\
{\Rightarrow}&{x}
&{}& {}& {~=~}
&{\frac{4m-16}{4m+3}}&{}&{}&{} \\
\end{array}$
• We can write: x coordinate of Q is: $\frac{4m-16}{4m+3}$
• In this problem, we do not need to find the y coordinate of Q.
5. Now we have the required x coordinates:
♦ From (3) we have the x coordinate of P.
♦ From (4) we have the x coordinate of Q.
• The average of these two quantities will be the x coordinate of R (Recall the mid-point formula)
• So we can write:
$\begin{array}{ll}
{}&{\text{x coordinate of R}}
&{}={}& {\frac{\frac{m-1}{m-5}~+~\frac{4m-16}{4m+3}}{2}}
&{} \\
{}&{}
&{}={}& {\frac{\frac{(m-1)(4m+3)~+~(4m-16)(m-5)}{(m-5)(4m+3)}}{2}}
&{} \\
{}&{}
&{}={}& {\frac{(m-1)(4m+3)~+~(4m-16)(m-5)}{2(m-5)(4m+3)}}
&{} \\
{}&{}
&{}={}& {\frac{(4m^2 + 3m - 4m - 3)~+~(4m^2 - 20m - 16m + 80)}{2(4m^2 + 3m - 20m - 15)}}
&{} \\
{}&{}
&{}={}& {\frac{(4m^2 - m - 3)~+~(4m^2 - 36m + 80)}{2(4m^2 - 17m - 15)}}
&{} \\
{}&{}
&{}={}& {\frac{8m^2 - 37m + 77}{8m^2 - 34m - 30}}
&{} \\
\end{array}$
6. Thus the x coordinate of R is $\frac{8m^2 - 37m + 77}{8m^2 - 34m - 30}$.
• But x coordinate of R is given as 1. So we can equate them:
$\begin{array}{ll}
{}&{\frac{8m^2 - 37m + 77}{8m^2 - 34m - 30}}
&{}={}& {1}
&{} \\
{\Rightarrow}&{8m^2 - 37m + 77}
&{}={}&
{8m^2 - 34m - 30}
&{} \\
{\Rightarrow}&{- 37m + 77}
&{}={}&
{- 34m - 30}
&{} \\
{\Rightarrow}&{77 + 30}
&{}={}&
{37m - 34m}
&{} \\
{\Rightarrow}&{107}
&{}={}&
{3m}
&{} \\
{\Rightarrow}&{m}
&{}={}&
{\frac{107}{3}}
&{} \\
\end{array}$
7. We have obtained the value of 'm'. So based on the result in (2), we can obtain the required equation:
$\begin{array}{ll}
{}&{mx - y}
&{}={}& {m-5}
&{} \\
{\Rightarrow}&{\left( \frac{107}{3} \times x \right) - y}
&{}={}&
{\frac{107}{3} - 5}
&{} \\
{\Rightarrow}&{107x - 3y}
&{}={}&
{107 - 15}
&{} \\
{\Rightarrow}&{107x - 3y -92}
&{}={}&
{0}
&{} \\
\end{array}$
8. The actual plot is shown below:
 |
| Fig.10.49 |
Solved example 10.25
Show that the path of a moving point such that it's distances from two lines 3x-2y=5 and 3x+2y=5 are equal is a straight line.
Solution:
1. In the rough sketch below,
• The yellow line is the path of a moving point.
• The line 3x-2y-5=0 is shown in red color.
• The line 3x+2y-5=0 is shown in green color.
 |
| Fig.10.50 Rough sketch |
2. Let us consider the distances:
• When the point is at A(x1,y1),
♦ it's distance from the red line is AA'.
♦ it's distance from the green line is AA''.
✰ We are give that, AA' = AA''.
• When the point is at B(x2,y2),
♦ it's distance from the red line is BB'.
♦ it's distance from the green line is BB''.
✰ We are give that, BB' = BB''
3. Which ever be the point on the yellow line, the distances from the red and green lines will be equal.
• So let us consider a general point P(x,y)
◼ Distance of P from the red line is PP'. It can be calculated as follows:
$\begin{array}{ll}
{}&{PP'}
&{}={}& {\frac{\left|Ax_1 + B x_1 + C \right|}{\sqrt{A^2 + B^2}}}
&{} \\
{}&{}
&{}={}& {\frac{\left|3x - 2y - 5 \right|}{\sqrt{3^2 + 2^2}}}
&{} \\
{}&{}
&{}={}& {\frac{\left|3x - 2y - 5 \right|}{\sqrt{13}}}
&{} \\
\end{array}$
◼ Distance of P from the green line is PP''. It can be calculated as follows:
$\begin{array}{ll}
{}&{PP''}
&{}={}& {\frac{\left|Ax_1 + B x_1 + C \right|}{\sqrt{A^2 + B^2}}}
&{} \\
{}&{}
&{}={}& {\frac{\left|3x + 2y - 5 \right|}{\sqrt{3^2 + 2^2}}}
&{} \\
{}&{}
&{}={}& {\frac{\left|3x + 2y - 5 \right|}{\sqrt{13}}}
&{} \\
\end{array}$
4. The two distances PP' and PP'' will be equal. So we can write:
$\begin{array}{ll}
{}&{PP'}
&{}={}& {PP''}
&{} \\
{\Rightarrow}&{\frac{\left|3x - 2y - 5 \right|}{\sqrt{13}}}
&{}={}& {\frac{\left|3x + 2y - 5 \right|}{\sqrt{13}}}
&{} \\
{\Rightarrow}&{\left|3x - 2y - 5 \right|}
&{}={}& {\left|3x + 2y - 5 \right|}
&{} \\
\end{array}$
5. The above result gives us two possibilities:
(i) 3x - 2y - 5 = 3x + 2y - 5
(ii) 3x - 2y - 5 = -(3x + 2y - 5)
• From (i) we get: 4y = 0, which gives y = 0
• From (ii) we get: 6x = 10, which gives x = 5/3
6. So there are two possibilities for the yellow line. We can write:
• If a point moves along the line y = 0, it's distances from two lines 3x-2y=5 and 3x+2y=5 will be equal.
♦ Note that, y = 0 is the x-axis.
• If a point moves along the line x = 5/3, it's distances from two lines 3x-2y=5 and 3x+2y=5 will be equal.
♦ Note that, x = 5/3 is a vertical line.
7. The actual plot is shown below:
 |
| Fig.10.51 |
Link to a few more solved examples is given below:
Miscellaneous Exercise on Chapter 10 - Part I
Miscellaneous Exercise on Chapter 10 - Part II
In the next chapter, we will see conic sections.