Chapter 5.6 - Quadratic Equations

In the previous section, we completed a discussion on polar representation. In this section, we will see quadratic equation.

Some basics can be written in 6 steps:
1. Consider the general form of quadratic equations: $ax^2+bx+c=0$
We know that the solutions of this type of equations are given by:
$x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
2. We see that, square root of b²-4ac is involved.
• This b²-4ac is called the discriminant of the quadratic equation.
    ♦ If the discriminant is greater than zero, there will be two real solutions.
    ♦ If the discriminant is equal to zero, there will be one real solution.
3. In some cases, b²-4ac may be less than zero. We know how to proceed in such cases. We saw it in section 5.1 of this chapter.

Now we will see some solved examples:

Solved Example 5.8
Solve $x^2+2=0$
Solution:
1. The given equation can be written as: $x^2=-2$
2. Taking square roots on both sides, we get:
$x=\pm \sqrt{-2}$
3. So we can write:
The solutions are: $x=\sqrt{-2}~~ \text{and}~~-\sqrt{-2}$
4. But $\sqrt{-2}$ is $\sqrt{2}\,i$
• So we get:
The solutions are: $x=\sqrt{2}\,i~~ \text{and}~~-\sqrt{2}\,i$

Solved Example 5.9
Solve $x^2+x+1=0$
Solution:
1. From the given equation, we get: a = 1, b= 1 and c = 1
• So the discriminant of the given equation is:
$b^2-4ac~=~(1)^2 -4 × 1 × 1~=~1-4~=~-3$
2. We can write:
$x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}~=~\frac{-1 \pm \sqrt{-3}}{2 × 1}~=~\frac{-1 \pm \sqrt{3}\,i}{2}$
3. So the solutions are:
$x~=~\frac{-1 + \sqrt{3}\,i}{2}~~ \text{and}~~\frac{-1 - \sqrt{3}\,i}{2}$

Check:
◼ First we will put $\frac{-1 + \sqrt{3}\,i}{2}$ in the place of x:
$\begin{array}{ll}
x^2&{}={}&\left(\frac{-1 + \sqrt{3}\,i}{2} \right)^2& {} &{} \\
\phantom{x^2}&{}={}& \left(\frac{-1}{2} + \frac{\sqrt{3}\,i}{2} \right)^2&{} \\
\phantom{x^2}&{}={}& \left(\frac{-1}{2}\right)^2~ +~2 × \frac{-1}{2} × \frac{\sqrt{3}\,i}{2}~+~\left(\frac{\sqrt{3}\,i}{2} \right)^2&{} \\
\phantom{x^2}&{}={}& \frac{1}{4}~ -~\frac{\sqrt{3}\,i}{2}~-~\frac{3}{4}&{} \\
\phantom{x^2}&{}={}& -\frac{1}{2}~ -~\frac{\sqrt{3}\,i}{2}&{} \\
\end{array}$
• Thus we get:
$\begin{array}{ll}
x^2+x+1&{}={}&-\frac{1}{2}~ -~\frac{\sqrt{3}\,i}{2}~+~\frac{-1}{2} + \frac{\sqrt{3}\,i}{2}~+~1& {} &{} \\
\phantom{x^2+x+1}&{}={}& -\frac{1}{2}~-~\frac{1}{2}~+~1&{} \\
\phantom{x^2+x+1}&{}={}& -1~+~1&{} \\
\phantom{x^2+x+1}&{}={}&0&{} \\
\end{array}$
• So $\frac{-1 + \sqrt{3}\,i}{2}$ is indeed a solution.
• In the same way we can check $\frac{-1 - \sqrt{3}\,i}{2}$ also.

◼ We can write:
    ♦ If the discriminant is less than zero, there will be two imaginary solutions.

Solved Example 5.10
Solve $\sqrt{5}x^2+x+\sqrt{5}=0$
Solution:
1. From the given equation, we get: a = $\sqrt{5}$, b= 1 and c = $\sqrt{5}$
• So the discriminant of the given equation is:
$b^2-4ac~=~(1)^2 -4 × \sqrt{5} × \sqrt{5}~=~1-4 × 5~=~1-20~=~-19$
2. We can write:
$x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}~=~\frac{-1 \pm \sqrt{-19}}{2 × \sqrt{5}}~=~\frac{-1 \pm \sqrt{19}\,i}{2 \sqrt{5}}$
3. So the solutions are:
$x~=~\frac{-1 + \sqrt{19}\,i}{2 \sqrt{5}}~~ \text{and}~~\frac{-1 - \sqrt{19}\,i}{2 \sqrt{5}}$

---

The link below gives a PDF file with more solved examples:

Exercise 5.3

---

Now we will see some miscellaneous examples from the topics that we saw in this chapter.

Solved example 5.11
Find the conjugate of $\frac{(3-2i)(2+3i)}{(1+2i)(2-i)}$
Solution:
1. First we will simplify the numerator:
$\begin{array}{ll}
(3-2i)(2+3i)&{}={}&6+9i-4i-6i^2& {} &{} \\
\phantom{(3-2i)(2+3i)}&{}={}&6+5i+6&{} \\
\phantom{(3-2i)(2+3i)}&{}={}&12+5i&{} \\
\end{array}$
2. Next we will simplify the denominator:
$\begin{array}{ll}
(1+2i)(2-i)&{}={}&2-i+4i-2i^2& {} &{} \\
\phantom{(1+2i)(2-i)}&{}={}&2+3i+2&{} \\
\phantom{(1+2i)(2-i)}&{}={}&4+3i&{} \\
\end{array}$
3. Now the given expression become: $\frac{12+5i}{4+3i}$
4. This can be written in the form x+yi:
$\begin{array}{ll}
\frac{12+5i}{4+3i}&{}={}&\frac{12+5i}{4+3i} × \frac{4-3i}{4-3i}& {} &{} \\
\phantom{\frac{12+5i}{4+3i}}&{}={}&\frac{48-36i+20i-15i^2}{16-9i^2}&{} \\
\phantom{\frac{12+5i}{4+3i}}&{}={}&\frac{48-16i+15}{16+9}&{} \\
\phantom{\frac{12+5i}{4+3i}}&{}={}&\frac{63-16i}{25}&{} \\
\phantom{\frac{12+5i}{4+3i}}&{}={}&\frac{63}{25}-\frac{16i}{25}&{} \\
\end{array}$
5. Now the conjugate can be written as: $\frac{63}{25}+\frac{16i}{25}$

Solved example 5.12
Find the modulus and argument of the complex numbers:
(i) $\frac{1+i}{1-i}$ (ii) $\frac{1}{1+i}$
Solution:
Part (i):
1. The given expression can be written in the form x+yi':
$\begin{array}{ll}
\frac{1+i}{1-i}&{}={}&\frac{1+i}{1-i} × \frac{1+i}{1+i}& {} &{} \\
\phantom{\frac{1+i}{1-i}}&{}={}&\frac{1+2i+i^2}{1-i^2}&{} \\
\phantom{\frac{1+i}{1-i}}&{}={}&\frac{1+2i-1}{1+1}&{} \\
\phantom{\frac{1+i}{1-i}}&{}={}&\frac{1+2i-1}{1+1}&{} \\
\phantom{\frac{1+i}{1-i}}&{}={}&\frac{2i}{2}&{} \\
\phantom{\frac{1+i}{1-i}}&{}={}&i&{} \\
\phantom{\frac{1+i}{1-i}}&{}={}&0+i&{} \\
\end{array}$
2. The complex number does not have a real part. So it lies on the y axis.
• Since the coefficient of i is '+1', the complex number lies on the +ve side of the y axis.
• Since it lies on the +ve side of the y axis, the argument $\theta=\frac{\pi}{2}$
3. Since the coefficient of i is '1', the complex number lies at a distance of at a distance of 1 unit from the origin. So modulus r = 1
• This is shown in fig.5.8(a) below:

Fig.5.8

Part(ii):
1. The given expression can be written in the form x+yi':
$\begin{array}{ll}
\frac{1}{1+i}&{}={}&\frac{1}{1+i} × \frac{1-i}{1-i}& {} &{} \\
\phantom{\frac{1}{1+i}}&{}={}&\frac{1-i}{1-i^2}&{} \\
\phantom{\frac{1}{1+i}}&{}={}&\frac{1-i}{1+1}&{} \\
\phantom{\frac{1}{1+i}}&{}={}&\frac{1-i}{2}&{} \\
\phantom{\frac{1}{1+i}}&{}={}&\frac{1}{2}\,-\,\left(\frac{1}{2} \right)i&{} \\
\end{array}$
2. Now the complex number is in the form x+yi. If we can find the modulus (r) and argument (𝜽), we can write it in the polar form:
r[cos 𝜽 + i sin 𝜽]
3. Since the two forms are equal, we can equate the corresponding parts:
    ♦ Equating the real parts, we get: x = r cos 𝜽
    ♦ Equating the imaginary parts, we get: y = r sin 𝜽
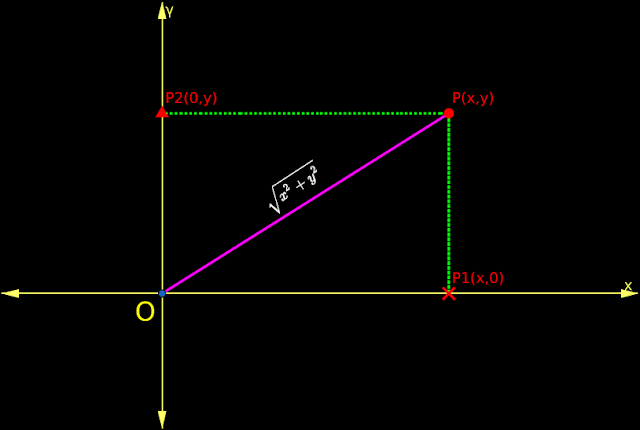
4. We know that $r=|z|=\sqrt{x^2+y^2}$
• So in our present case, we get:
$r=\sqrt{\left(\frac{1}{2} \right)^2+\left(\frac{1}{2} \right)^2}=\sqrt{\frac{1}{4}+\frac{1}{4}}=\sqrt{\frac{1}{2}}=\pm \frac{1}{\sqrt{2}}$
• r is the distance between the complex number and the origin. A distance cannot be -ve. So we can write: $r= \frac{1}{\sqrt{2}}$
5. From the results in (3), we get:
(i) $x=\frac{1}{2}=\frac{1}{\sqrt{2}} \cos \theta$
(ii) $y=-\frac{1}{2}=\frac{1}{\sqrt{2}} \sin \theta$
• cos 𝜽 is +ve and sin 𝜽 is -ve. So it lies in the fourth quadrant.
6. Taking ratios, (ii) to (i), we get:
$\frac{\frac{1}{\sqrt{2}} \sin \theta}{\frac{1}{\sqrt{2}} \cos \theta}=\frac{-\frac{1}{2}}{\frac{1}{2}}$
$\Rightarrow \tan \theta = -1$
• This is a trigonometrical equation. We learned to solve them in chapter 3. (Details here)
7. We know that, $\tan \frac{\pi}{4}=1$
• We have the identity: tan (π-𝜽) = -tan 𝜽
If we put $\theta = \frac{\pi}{4}$, we get:
$\tan \left(\pi - \frac{\pi}{4}  \right)=-\tan \frac{3\pi}{4} = -1$
$\Rightarrow \tan \left(\frac{3\pi}{4}  \right)=-tan \frac{\pi}{4} = -1$
$\Rightarrow \tan \theta = \tan \left(\frac{3\pi}{4}  \right) = -1$
• From this we get: $\theta = \frac{3\pi}{4}$
• This value of 𝜽 lies in the second quadrant. So it is not acceptable.
8. There is another possible value for 𝜽. It can be calculated using the identity: tan 𝜽 = tan (π+𝜽)
• So we can write:
$\tan \frac{3\pi}{4}=\tan \theta = \tan \left(\pi + \theta \right)= \tan \left(\pi + \frac{3\pi}{4}\right) = -1$
• From this we get: $\tan \theta = \tan \left( \frac{7\pi}{4}\right) = -1$
• So $\theta = \frac{7\pi}{4}$
• This value of 𝜽 lies in the fourth quadrant. So it is acceptable.
9. Thus we get the values of r and 𝜽:
   ♦ From (4), we get: $r= \frac{1}{\sqrt{2}}$
   ♦ From (7),we get: $\theta = \frac{7\pi}{4}$
10. $\theta = \frac{7\pi}{4}$ indicates that, the complex number is in the fourth quadrant. When a complex number is in the fourth quadrant, we assume the angle of rotation to be clockwise.
• Thus we get: $2\pi-\frac{7\pi}{4}~=~-\frac{\pi}{4}$
• So angle of rotation is $-\frac{\pi}{4}$
11. So the required values are:
   ♦ From (4), we get: $r= \frac{1}{\sqrt{2}}$
   ♦ From (9),we get: $\theta = -\frac{\pi}{4}$
• This is shown in fig.5.8(b) above.

---

In the next section, we will see a few more miscellaneous examples.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 5.5 - Polar Representation of A Complex Number

In the previous section, we saw the details about Argand plane. In this section, we will see Polar representation.

Some basics can be written in 9 steps:
1. In fig.5.4 below, P(x,y) represents the complex number z = x+yi

Fig.5.4

• We have seen that, OP will be the modulus of z.
• Let the length of OP be r. Then we can write: OP = r = |z|
• PP₁ is the perpendicular dropped from P onto the x axis.
• PP₂ is the perpendicular dropped from P onto the y axis.
2. Let OP make an angle of 𝜽 radians with the positive side of the x axis.
• Then we get:
   ♦ OP₁ = r cos 𝜽
   ♦ PP₁ = r sin 𝜽
3. Now we can write the complex number in terms of r and 𝜽:
   ♦ OP₁ = x. So we get x = r cos 𝜽
   ♦ PP₁ = OP₂ = y. So we get: y = r sin 𝜽
• Then the complex number z = x+yi can be written as: r cos 𝜽 + r i sin 𝜽
   ♦ This is same as: z = r(cos 𝜽 + i sin 𝜽)
4. So we have two methods to represent a complex number:
(i) z = x+yi
(ii) z = r(cos 𝜽 + i sin 𝜽)
• In the first method, two distances (x and y) will give the complex number.
   ♦ That is., the ordered pair (x,y) will give the complex number.
• In the second method, a distance (r) and an angle (𝜽) will give the complex number.
   ♦ That is., the ordered pair (r,𝜽) will give the complex number.
[Since 𝜽 is measured in radians, it will be a real number. So (r,𝜽) is an ordered pair of real numbers.]
• We have already seen that, r (which is the modulus) can be calculated using x and y as: $|z|=\sqrt{x^2+y^2}$
5. Writing a complex number in the form  r(cos 𝜽 + i sin 𝜽) is called polar representation of a complex number.
• (r,𝜽) is called polar coordinates of the complex number.
• The origin is considered as the pole.
• 𝜽 should be measured from the +ve direction of the x axis.
   ♦ 𝜽 is called the argument of the complex number z.
   ♦ 𝜽 is also called the amplitude of the complex number z.
6. In the above five steps, the complex number that we considered was in the first quadrant.
• But we may have to deal with complex numbers which are in the second, third or fourth quadrants also. This is shown in fig.5.5 below: 

Fig.5.5

• So 𝜽 can be any value between 0 and 2π.
• 𝜽 can be zero also. (This happens when the complex number is on the positive side of the x axis)
7. In chapter 3, we have seen that, even if 𝜽 is greater than $\frac{\pi}{2}$,
   ♦ cosine will give the x coordinate of P   
   ♦ sine will give the y coordinate of P
   ♦ (Details here)   
• So even if 𝜽 (argument) of a complex number is greater than $\frac{\pi}{2}$, we can use the polar representation for that complex number.
8. In chapter 3, we also saw that, 𝜽 can be greater than 2π. But then the results will be same as completing one or more full rotations.
• So we will need only those values 'which are between 0 and 2π'. It will take care of all the four quadrants.
9. However, while dealing with complex numbers, mathematicians prefer another method. It can be written in 3 steps:
(i) If P is in the first or second quadrants, the argument is considered to be +ve.
• That is.,
    ♦ the rotation starts from the +ve side of the x axis in the anti-clockwise direction.
    ♦ the rotation ends at the -ve side of the x axis.    
(ii) If P is in the third or fourth quadrants, the argument is considered to be -ve.
• That is.,
    ♦ the rotation starts from the +ve side of the x axis in the clockwise direction.   
    ♦ the rotation ends at the -ve side of the x axis.
(iii) This method will also take care of all the four quadrants. It is shown in fig.5.6 below:

Fig.5.6

---

Now we will see some solved examples

Solved example 5.6
Represent the complex number $z=1+\sqrt{3}\,i$ in the polar form.
Solution:
1. The complex number is given to us in the form x+yi. We have to convert it into the form:
r[cos 𝜽 + i sin 𝜽]
• For that, we have to find the polar coordinates (r,𝜽)
2. Since the two forms are equal, we can equate the corresponding parts:
    ♦ Equating the real parts, we get: x = r cos 𝜽
    ♦ Equating the imaginary parts, we get: y = r sin 𝜽
3. We know that $r=|z|=\sqrt{x^2+y^2}$
• So in our present case, we get:
$r=\sqrt{1^2+(\sqrt{3})^2}=\sqrt{1+3}=\sqrt{4}=\pm 2$
• r is the distance between the complex number and the origin. A distance cannot be -ve. So we can write: r = 2 
4. From the results in (2), we get:
(i) $x=1=2 \cos \theta$
(ii) $y=\sqrt{3}=2 \sin \theta$
• We must find that value of 𝜽 which satisfies both (i) and (ii)
5. Taking ratios, (ii) to (i), we get:
$\frac{2 \sin \theta}{2 \cos \theta}=\frac{\sqrt{3}}{1}$
$\Rightarrow \tan \theta = \sqrt{3}$
• This is a trigonometrical equation. We learned to solve them in chapter 3. (Details here)
6. We know that, $\tan \frac{\pi}{3}=\sqrt{3}$
• So we can write: $\tan \frac{\pi}{3}=\tan \theta = \sqrt{3}$
• From this we get: $\theta = \frac{\pi}{3}$
Check:
• Substituting this value of 𝜽 in 4(i), we get:
$1=2 \cos \frac{\pi}{3} = 2 × \frac{1}{2} = 1$. This is true.
• Substituting this value of 𝜽 in 4(ii), we get:
$\sqrt{3}=2 \sin \frac{\pi}{3} = 2 × \frac{\sqrt{3}}{2} = \sqrt{3}$. This is true.
• So $\theta = \frac{\pi}{3}$ is acceptable.
7. There is another possible value for 𝜽. It can be calculated using the identity: tan 𝜽 = tan (π+𝜽)
• So we can write:
$\tan \frac{\pi}{3}=\tan \theta = \tan \left(\pi + \theta \right)= \tan \left(\pi + \frac{\pi}{3}\right) = \sqrt{3}$
• From this we get: $\tan \theta = \tan \left( \frac{4\pi}{3}\right) = \sqrt{3}$
• So $\theta = \frac{4\pi}{3}$
Check:
• Substituting this value of 𝜽 in 4(i), we get:
$1=2 \cos \frac{4\pi}{3} = 2 × -\frac{1}{2} = -1$. This is not true.
• Substituting this value of 𝜽 in 4(ii), we get:
$\sqrt{3}=2 \sin \frac{4\pi}{3} = 2 × - \frac{\sqrt{3}}{2} = -\sqrt{3}$. This is not true.
• Value of 𝜽 will be acceptable only if both equations 4(i) and 4(ii) are satisfied. So $\theta = \frac{4\pi}{3}$ is not acceptable.
8. Thus we get the values of r and 𝜽:
   ♦ From (3), we get: r = 2
   ♦ From (6),we get: $\theta = \frac{4\pi}{3}$
9. So the required polar form is: $z=2\left(\sin \frac{\pi}{3}+i \cos \frac{\pi}{3}  \right)$.
• The point P in fig.5.7(a) below represents the given complex number in the Argand plane.

Fig.5.7

---

In the above example, we had to perform two checks. Those two checks can be avoided by using a simple trick. This can be explained in 4 steps:
1. We saw that two values of 𝜽 are possible. This is because, tangent of 𝜽 can be $\sqrt{3}$ on two occasions:
(i) When 𝜽 = $\frac{\pi}{3}$  
(ii) When 𝜽 = $\frac{4\pi}{3}$
2. But only one value is acceptable because in total, three equations should be satisfied:
(i) $1=2 \cos \theta$
(ii) $\sqrt{3}=2 \sin \theta$
(iii) $\sqrt{3}=\tan \theta$
3. We see that both sin 𝜽 and cos 𝜽 are +ve.
• This is possible only when 𝜽 is in the first quadrant.
4. So we must choose that 𝜽 which is in the first quadrant.
• Using this trick, the two checks can be avoided.

---

Solved example 5.7
Convert the complex number $z=\frac{-16}{1+\sqrt{3}\,i}$ in the polar form.
Solution:
1. First we have to convert the given complex number into the form x+yi. It can be done as shown below:
$\begin{array}{ll}
\frac{-16}{1+\sqrt{3}\,i}&{}={}&\frac{-16}{1+\sqrt{3}\,i} × \frac{1-\sqrt{3}\,i}{1-\sqrt{3}\,i}& {} &{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& \frac{(-16)(1-\sqrt{3}\,i)}{1^2-(\sqrt{3})^2(i)^2}&{} \\
\phantom{\frac{1}{2-3i}}&{}&\color {green}{(a+b)(a-b)=a^2-b^2} &{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& \frac{(-16)(1-\sqrt{3}\,i)}{1-(3)(-1)}&{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& \frac{(-16)(1-\sqrt{3}\,i)}{4}&{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& -4(1-\sqrt{3}\,i)&{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& -4+4\sqrt{3}\,i&{} \\
\end{array}$
2. Now the complex number is in the form x+yi. We have to convert this into the form:
r[cos 𝜽 + i sin 𝜽]
• For that, we have to find the polar coordinates (r,𝜽)
3. Since the two forms are equal, we can equate the corresponding parts:
    ♦ Equating the real parts, we get: x = r cos 𝜽
    ♦ Equating the imaginary parts, we get: y = r sin 𝜽
4. We know that $r=|z|=\sqrt{x^2+y^2}$
• So in our present case, we get:
$r=\sqrt{(-4)^2+(4\sqrt{3})^2}=\sqrt{16+(16 × 3)}=\sqrt{64}=\pm 8$
• r is the distance between the complex number and the origin. A distance cannot be -ve. So we can write: r = 8 
5. From the results in (3), we get:
(i) $x=-4=8 \cos \theta$
(ii) $y=4\sqrt{3}=8 \sin \theta$
• cos 𝜽 is -ve and sin 𝜽 is +ve. So 𝜽 is in the second quadrant.
6. Taking ratios, (ii) to (i), we get:
$\frac{8 \sin \theta}{8 \cos \theta}=\frac{4\sqrt{3}}{-4}$
$\Rightarrow \tan \theta = -\sqrt{3}$
• This is a trigonometrical equation. We learned to solve them in chapter 3. (Details here)
7. We know that, $\tan \frac{\pi}{3}=\sqrt{3}$
• We have the identity: tan (π-𝜽) = -tan 𝜽
If we put $\theta = \frac{\pi}{3}$, we get:
$\tan \left(\pi - \frac{\pi}{3}  \right)=-\tan \frac{\pi}{3} = -\sqrt{3}$
$\Rightarrow \tan \left(\frac{2\pi}{3}  \right)=-tan \frac{\pi}{3} = -\sqrt{3}$
$\Rightarrow \tan \theta = \tan \left(\frac{2\pi}{3}  \right) = -\sqrt{3}$
• From this we get: $\theta = \frac{2\pi}{3}$
8. There is another possible value for 𝜽. It can be calculated using the identity: tan 𝜽 = tan (π+𝜽)
• So we can write:
$\tan \frac{2\pi}{3}=\tan \theta = \tan \left(\pi + \theta \right)= \tan \left(\pi + \frac{2\pi}{3}\right) = -\sqrt{3}$
• From this we get: $\tan \theta = \tan \left( \frac{5\pi}{3}\right) = -\sqrt{3}$
• So $\theta = \frac{5\pi}{3}$
9. So we have two values:
• From (7), we have: $\theta = \frac{2\pi}{3}$
    ♦ This is in the second quadrant.
• From (8), we have: $\theta = \frac{5\pi}{3}$
    ♦ This is in the fourth quadrant.
10. In step (5), we saw that 𝜽 is in the second quadrant.
• So $\theta = \frac{2\pi}{3}$ is the acceptable value.
11. Thus we get the values of r and 𝜽:
   ♦ From (4), we get: r = 8
   ♦ From (10),we get: $\theta = \frac{2\pi}{3}$
12. So the required polar form is: $z=8\left(\sin \frac{2\pi}{3}+i \cos \frac{2\pi}{3}  \right)$.
• The point P in fig.5.7(b) above represents the given complex number in the Argand plane.

---

The link below gives a PDF file with more solved examples:

Exercise 5.2

---

• In the next section, we will see quadratic equations.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 5.4 - The Argand Plane

In the previous section, we saw modulus and conjugate of complex numbers. In this section, we will see Argand plane.

Some basics about Argand plane can be written in 7 steps:
1. We are familiar with Cartesian plane and ordered pairs.
• The Cartesian plane is formed by two perpendicular axes.
    ♦ The horizontal x axis.
    ♦ The vertical y axis.
• Ordered pairs like (2,3), (5, -1) etc., occupy unique positions in the Cartesian plane.
2. In our present case, we have complex numbers.
• The complex numbers have a real part and an imaginary part. These two parts can be written as an ordered pair.
• For example,
    ♦ The ordered pair related to 5+7i will be (5,7)
    ♦ The ordered pair related to 2-3i will be (2,-3)  
    ♦ The ordered pair related to -8-3i will be (-8,-3)
• The x coordinate of the ordered pair is the real part.
• The y coordinate of the ordered pair is the imaginary part.
• Since they are written as ordered pairs, we can mark them on a plane.
3. We cannot use Cartesian plane because, in a Cartesian plane, both x and y coordinates are real numbers.
    ♦ All numbers on the x axis are real numbers.
    ♦ All numbers on the y axis are real numbers.
4. So we develop a new plane called Argand plane.
• Like the Cartesian plane, the Argand plane is also formed by two perpendicular axes.
    ♦ The horizontal x axis is known as the real axis.
    ♦ The vertical y axis is known as the imaginary axis.
5. Let us see how a complex number say 4+3i is marked on the Argand plane. It can be written in 5 steps:
(i) We know that, in the complex number 4+3i, the real part is  ‘4’.
    ♦ So we mark 4 at the correct position on the real axis.
    ♦ This is indicated by the ❌ mark in fig.5.1 below:

Fig.5.1

(ii) We know that, in the complex number 4+3i, the imaginary part is  ‘3’.
    ♦ So we mark 3 at the correct position on the imaginary axis.
    ♦ This is indicated by the ⛰ mark.
(iii) Next we draw green dashed lines:
    ♦ Vertical green dashed line through 4
    ♦ Horizontal green dashed line through 3
(iv) The point of intersection of the two green dashed lines represents the complex number 4+3i
    ♦ This is indicated by the ● mark. It is labelled as A(4,3)
◼ The above process is already familiar to us. We have used it several times while working on Cartesian planes. If we use a graph paper, we will not need to draw horizontal and vertical green dashed lines.
(v) The point A(4,3) represents the complex number 4+3i
6. Five more complex numbers are marked in the fig.5.1
    ♦ B(-6,4) represents the complex number -6+4i
    ♦ C(-5,-3) represents the complex number -5-3i
    ♦ D(6,-2) represents the complex number 6-2i
    ♦ E(7,0) represents the complex number 7+0i
        ✰ Any complex number on the real axis will not have the imaginary part.
    ♦ F(0,2) represents the complex number 0+2i
        ✰ Any complex number on the imaginary axis will not have the real part.
7. We can write:
All points on the Argand plane will represent complex numbers.
• We can write the converse also:
If all points on a plane represent complex numbers, then that plane is called an Argand plane.
• The Argand plane is also known as Complex plane.

---

• So now we know how to represent a complex number on the Argand plane.
• Next we will see how to represent the modulus of a complex number on the Argand plane. It can written in 3 steps:

1. In fig.5.2 below, P(x,y) represents the complex number x+yi
    ♦ P₁ is the foot of the perpendicular from P on to the real axis.
    ♦ P₂ is the foot of the perpendicular from P on to the imaginary axis.
    ♦ A magenta line joins the origin O and P

Fig.5.2

2. Now we have a right triangle OP₁P. It is right angled at P₁
• The base of this right triangle is OP₁
    ♦ It’s length is x
• The altitude of this right triangle is PP₁
    ♦ It’s length = length of OP₂ = y
• So the length of OP (hypotenuse) will be $\sqrt{x^2+y^2}$
• The length OP is the distance between P and the origin O
◼ But $\sqrt{x^2+y^2}$ is the modulus of the complex number represented by P
3. So we can write:
    ♦ The distance between P and the origin
    ♦ will be the
    ♦ modulus of the complex number represented by P

---

• So now we know how to represent the modulus of a complex number on the Argand plane.
• Next we will see how to represent the conjugate of a complex number on the Argand plane. It can written in 7 steps:
1. In fig.5.3 below, P(x,y) represents the complex number x+yi

Fig.5.3

2. Drop a perpendicular from P on to the real axis.
Let P₁ be the foot of the perpendicular.
3. Extend the line PP₁ downwards upto P` on such a way that, PP₁ = P₁P'
4. Now we can write three points:
(i) Points P and P' lie on opposite sides of the real axis.
(ii) Both P and P' lie on the line perpendicular to the real axis.
(iii) Both P and P` are at equal distances from the real axis.
5. Based on the three points above, we can write:
P' is the mirror image of P. The real axis being the mirror line.
6. The coordinates of P' are: (x,-y)
• So P' represent the complex number x-yi
7. But x-yi is the conjugate of x+yi
• So we can write:
The conjugate of a complex number is represented by the mirror image of that complex number. The real axis being the mirror line.

---

In the next section, we will see polar representation of complex numbers.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 5.3 - The Modulus and Conjugate of a Complex Number

In the previous section, we saw the  the algebraic operations on complex numbers. We also saw identities related to complex numbers. In this section, we will see modulus and conjugate of a complex number.

Modulus of a complex number

This can be written in 3 steps:
1. Consider the complex number a+bi
• We can take out 'a' and 'b' and then calculate $\sqrt{a^2+b^2}$.
2. Since 'a' and 'b' are real numbers and since they are being squared and added, this $\sqrt{a^2+b^2}$ will be a +ve real number.
• This +ve real number is called the modulus of the complex number a+bi
3. Modulus of any complex number z is denoted as: |z|
• So we can write:
If $z=a+bi$, then $|z|=\sqrt{a^2+b^2}$
• Let us see some examples:
   ♦ If z = 2+i, then |z| = |2+i| = $\sqrt{2^2+1^2}=\sqrt{4+1}=\sqrt{5}$  
   ♦ If z = 3-7i, then |z| = |3-7i| = $\sqrt{3^2+(-7)^2}=\sqrt{9+49}=\sqrt{58}$  

Conjugate of a complex number

This can be written in 4 steps:
1. Consider the complex number a+bi
• We can take out 'a' and 'b' and using them, form a new complex number.
2. This new complex number is such that:
    ♦ Real part is the same a
    ♦ Imaginary part is the same b but with sign reversed
3. So the new complex number will be a-bi
• This new complex number is the conjugate of the given complex number a+bi
4. Conjugate of any complex number is denoted as: $\bar{z}$
• So we can write:
If $z=a+bi$, then $\bar{z}=a-bi$
• Let us see some examples:
   ♦ If z = 2+i, then $\bar{z}=\overline{2+i}=2-i$  
   ♦ If z = 3-7i, then $\bar{z}=\overline{3-7i}=3+7i$  

---

Relation between $\mathbf{z,~\frac{1}{z},~\bar{z}~\text{and}~|z|}$

This can be written in 3 steps:
1. Consider the complex number z = a+bi
We know that, it's multiplicative inverse will be: $\frac{1}{z}=\left[\frac{a}{a^2+b^2}~+~\left(\frac{-b}{a^2+b^2} \right)i \right]$
2. The multiplicative inverse consists of two fractions. Since the denominators are the same, we can easily combine them.
• We get: $\frac{1}{z}=\left[\frac{a-bi}{a^2+b^2} \right]$
   ♦ The numerator on the right side is $\bar{z}$
   ♦ The denominator on the right side is $|z|^2$
3. Thus we get:$\frac{1}{z}=\frac{\bar{z}}{|z|^2}$
• Rearranging this, we get: $|z|^2=z\bar{z}$

---

In addition to the above relation, we can derive six more results:

1. $\left|z_1 z_2\right| = \left|z_1\right| × \left|z_2\right|$
• Let us see an example:
   ♦ If z₁ = 3+4i and z₂ = 12+5i, then z₁z₂ = 16+63i
   ♦ (We already know how to calculate z₁z₂)
   ♦ |z₁| = $\sqrt{3^2+4^2}=\sqrt{25}$ = 5
   ♦ |z₂| = $\sqrt{12^2+5^2}=\sqrt{169}$ = 13
   ♦ |z₁z₂| = $\sqrt{16^2+63^2}=\sqrt{4225}$ = 65
   ♦ 65 = 5  × 13

2. $\left| \frac{z_1}{z_2}\right|=\frac{|z_1|}{|z_2|}$  Provided |z₂| ≠ 0
• Let us see an example:
(i) Let z₁ = 3+4i and z₂ = 12+5i
First we calculate $\frac{1}{z_2}$, which is the multiplicative inverse of z₂:
$\begin{array}{ll}
\frac{1}{z_2}&{}={}&\frac{1}{12+5i}& {} &{} \\
\phantom{\frac{1}{z_2}}&{}={}& \frac{12}{12^2+5^2}~+~\frac{-5i}{12^2+5^2} &{} \\
\phantom{\frac{1}{z_2}}&{}={}& \frac{12}{169}+\frac{-5i}{169} &{} \\
\end{array}$
(ii) So $ \frac{z_1}{z_2} = z_1 × \frac{1}{z_2}= (3+4i) × \left(\frac{12}{169}+\frac{-5i}{169}\right)$
This works out to $\frac{32}{97}+\frac{17i}{87}$
(iii) Thus $\left| \frac{z_1}{z_2}\right|=\left| \frac{32}{97}+\frac{17i}{87}\right|=\frac{5}{13}$
(iv) Next we calculate individual moduli:
|z₁| = |3+4i| = 5
|z₂| = |12+5i| = 13
(v) Thus we get: $\left| \frac{z_1}{z_2}\right|=\frac{|z_1|}{|z_2|}$

3. $\overline{z_1 z_2} = \bar{z_1} × \bar{z_2}$
• Let us see an example:
   ♦ If z₁ = 3+4i and z₂ = 12+5i, then z₁z₂ = 16+63i
   ♦ $\bar{z_1}=\overline{3+4i}=3-4i$
   ♦ $\bar{z_2}=\overline{12+5i}=12-5i$
   ♦ $\bar{z_1} × \bar{z_2}=(3-4i) × (12-5i)=16-63i$ 
   ♦ $\overline{z_1z_2} = \overline{16+63i}=16-63i$

4. $\overline{z_1+z_2}=\bar{z_1}+\bar{z_2}$
• Let us see an example:
   ♦ If z₁ = 3+4i and z₂ = 12+5i, then z₁+z₂ = 15+9i
   ♦ $\bar{z_1}=3-4i$ and $\bar{z_2}=12-5i$
   ♦ $\bar{z_1}+\bar{z_2}=(3-4i)+(12-5i)=15-9i$
   ♦ $\overline{z_1+z_2}=\overline{15+9i}=15-9i$

5. $\overline{z_1-z_2}=\bar{z_1}-\bar{z_2}$
• Let us see an example:
   ♦ If z₁ = 3+4i and z₂ = 12+5i, then z₁-z₂ = -9-i
   ♦ $\bar{z_1}=3-4i$ and $\bar{z_2}=12-5i$
   ♦ $\bar{z_1}-\bar{z_2}=(3-4i)-(12-5i)=-9+i$
   ♦ $\overline{z_1-z_2}=\overline{-9-i}=-9+i$

6. $\overline{\left( \frac{z_1}{z_2}\right)}=\frac{\bar{z_1}}{\bar{z_2}}$  Provided z₂ ≠ 0
• Let us see an example:
(i) Let z₁ = 3+4i and z₂ = 12+5i
First we calculate $\frac{1}{z_2}$, which is the multiplicative inverse of z₂:
$\begin{array}{ll}
\frac{1}{z_2}&{}={}&\frac{1}{12+5i}& {} &{} \\
\phantom{\frac{1}{z_2}}&{}={}& \frac{12}{12^2+5^2}~+~\frac{-5i}{12^2+5^2} &{} \\
\phantom{\frac{1}{z_2}}&{}={}& \frac{12}{169}+\frac{-5i}{169} &{} \\
\end{array}$
(ii) So $ \frac{z_1}{z_2} = z_1 × \frac{1}{z_2}= (3+4i) × \left(\frac{12}{169}+\frac{-5i}{169}\right)$
This works out to $\frac{32}{97}+\frac{17i}{87}$
(iii) Thus $\overline{\left( \frac{z_1}{z_2}\right)}=\overline{\frac{32}{97}+\frac{17i}{87}}=\frac{32}{97}-\frac{17i}{87}$
(iv) Next we write the individual conjugates:
$\bar{z_1}=3-4i$ and $\bar{z_2}=12-5i$
(v) Now we get: $\frac{\bar{z_1}}{\bar{z_2}}=\frac{3-4i}{12-5i}=\frac{32}{97}-\frac{17i}{87}$
This is the same result obtained in (iii)

---

Let us see some solved examples:

Solved example 5.4
Find the multiplicative inverse of 2-3i
Solution:
1. Multiplicative inverse of any complex number z is denoted as: $\frac{1}{z}$
• It can be obtained using the equation: $\frac{1}{z}=\frac{\bar{z}}{|z|^2}$
2. So our first aim is to write $\bar{z}$
We have: $\bar{z} = \overline{2-3i} = 2+3i$
3. Next we calculate $|z|^2$
We have: $|z|^2=|2-3i|^2=(2^2 + (-3)^2)=(4+9)=13$
4. Thus we get: $\frac{1}{z}=\frac{\bar{z}}{|z|^2}=\frac{2+3i}{13}=\frac{2}{13}+\frac{3}{13}i$

Alternate method:
1. We want $\frac{1}{z}$, which is the reciprocal of z
• That means, we want $\frac{1}{2-3i}$
2. We need to write $\frac{1}{2-3i}$ in the form a+bi
• So we need to remove i from the denominator. For that, we can multiply both numerator and denominator by (2+3i)
3. Thus we get:
$\begin{array}{ll}
\frac{1}{2-3i}&{}={}&\frac{1(2+3i)}{(2-3i)(2+3i)}& {} &{} \\
\phantom{\frac{1}{2-3i}}&{}={}& \frac{(2+3i)}{2^2-(3i)^2}&{} \\
\phantom{\frac{1}{2-3i}}&{}&\color {green}{(a+b)(a-b)=a^2-b^2} &{} \\
\phantom{\frac{1}{2-3i}}&{}={}& \frac{(2+3i)}{4+9}&{} \\
\phantom{\frac{1}{2-3i}}&{}={}& \frac{(2+3i)}{13}&{} \\
\phantom{\frac{1}{2-3i}}&{}={}& \frac{2}{13}+\frac{3}{13}i&{} \\
\end{array}$

Solved example 5.5
Express the following in the form a+bi
(i) $\frac{5+\sqrt{2}\,i}{1-\sqrt{2}\,i}$  (ii) $i^{-35}$
Solution(i):
$\begin{array}{ll}
\frac{5+\sqrt{2}\,i}{1-\sqrt{2}\,i}&{}={}&\frac{(5+\sqrt{2}\,i)(1+\sqrt{2}\,i)}{(1-\sqrt{2}\,i)(1+\sqrt{2}\,i)}& {} &{} \\
\phantom{\frac{5+\sqrt{2}\,i}{1-\sqrt{2}\,i}}&{}={}& \frac{(5+\sqrt{2}\,i)(1+\sqrt{2}\,i)}{1^2-(\sqrt{2}\,i)^2}&{} \\
\phantom{\frac{1}{2-3i}}&{}&\color {green}{(a+b)(a-b)=a^2-b^2} &{} \\
\phantom{\frac{5+\sqrt{2}\,i}{1-\sqrt{2}\,i}}&{}={}& \frac{5+5\sqrt{2}\,i+\sqrt{2}\,i+(\sqrt{2}\,i)^2}{1-(2 × -1)}&{} \\
\phantom{\frac{5+\sqrt{2}\,i}{1-\sqrt{2}\,i}}&{}={}& \frac{5+5\sqrt{2}\,i+\sqrt{2}\,i+(2 × -1)}{1-(2 × -1)}&{} \\
\phantom{\frac{5+\sqrt{2}\,i}{1-\sqrt{2}\,i}}&{}={}& \frac{5+5\sqrt{2}\,i+\sqrt{2}\,i-2}{1+2}&{} \\
\phantom{\frac{5+\sqrt{2}\,i}{1-\sqrt{2}\,i}}&{}={}& \frac{3+6\sqrt{2}\,i}{3}&{} \\
\phantom{\frac{5+\sqrt{2}\,i}{1-\sqrt{2}\,i}}&{}={}& 1+2\sqrt{2}\,i&{} \\
\end{array}$

Solution(ii):
1. Dividing 35 by 4, we get: $35\div 4 = 8 \frac{3}{4}$
    ♦ So the remainder is 3
2. Thus $i^{-35}=\frac{1}{i^{35}}=\frac{1}{-i}$
3. Now we remove -i from the denominator:
$\frac{1}{-i}=\frac{1}{-i} × \frac{i}{i}=\frac{i}{-1 × i^2}=\frac{i}{-1 × -1}=\frac{i}{1}=i$

---

The link below gives some solved examples related to the topics that we have discussed so far in this chapter.

Exercise 5.1

---

• In the next section, we will see Argand plane and Polar representation.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

 

Chapter 5.2 - Division of two Complex Numbers

In the previous section, we saw complex numbers and some of their algebraic operations like addition, subtraction and multiplication. We also saw additive inverse and multiplicative inverse. In this section, we will see some more algebraic operations.

D. Division of two complex numbers.
This can be written in 2 steps:
1. If z₁ and z₂ are two complex numbers,
Then the quotient ${z_1}\div{z_2}$ is defined as: ${z_1}\div{z_2}=z_1 × \frac{1}{z_2}$
(Recall that, for 'division of real numbers' also, we use the reciprocal.
For example: $5 \div 2=5 × \frac{1}{2}$)
2. We have seen that, $\frac{1}{z_2}$ is the multiplicative inverse of z₂
• So we can write:
    ♦ If we want to divide z₁ by z₂,
    ♦ We must multiply z₁ by the multiplicative inverse of z₂
• Let us see an example:
If z₁ = 6+3i  and  z₂ = 2-i, find $\frac{z_1}{z_2}$
Solution:
• We have:
Multiplicative inverse of a+bi = $\frac{a}{a^2+b^2}~+~\left(\frac{-b}{a^2+b^2} \right)i$
• So the multiplicative inverse of 2-i = $\frac{2}{2^2+(-1)^2}~+~\left(\frac{-(-1)}{2^2+(-1)^2} \right)i$
= $\frac{2}{4+1}~+~\left(\frac{1}{4+1} \right)i$
= $\frac{2}{5}~+~\left(\frac{1}{5} \right)i$
• Thus we get:
$\begin{array}{ll}
\frac{6+3i}{2-i}&{}={}& (6+3i) × \left[\frac{2}{5}~+~\left(\frac{1}{5} \right)i \right]& {} \\
\phantom{\frac{6+3i}{2-i}}&{}={}& 6×\frac{2}{5}~-~3×\frac{1}{5}~+~\left[6×\frac{1}{5}~+~3×\frac{2}{5}\right] i &{} & {} \\
\phantom{\frac{6+3i}{2-i}}&{}={}& \frac{12}{5}~-~\frac{3}{5}~+~\left[\frac{6}{5}~+~\frac{6}{5}\right] i &{}& {} \\
\phantom{\frac{6+3i}{2-i}}&{}={}& \frac{9}{5}~+~\left[\frac{12}{5}\right] i &{}& {} \\
\end{array}$

E. Power of i
◼ First we will consider positive powers. It can be written in 7 steps:
1. We know that: $i=\sqrt{-1}$
2. So $i^2=\left(\sqrt{-1}\right)^2 = -1$
3. Then $i^3 = (i^2) i = (-1)i = -i$
4. $i^4 = \left(i^2 \right)^2 = (-1)^2 = 1$
5. Then $i^5 = (i^4)i = (1)i = i$
6. Then $i^6 = (i^5)i = (i)i = i^2 = -1$
7. We see that the result can be -1, -i, 1 and i

• Based on the above results, we can write:
If k is any integer, the general form can be written as:
   ♦ $i^{4k}=1$
   ♦ $i^{4k+1}=i$
   ♦ $i^{4k+2}=-1$
   ♦ $i^{4k+3}=-i$
• That means, we have to divide the power by 4
   ♦ If the remainder is 0, the result is 1
   ♦ If the remainder is 1, the result is i
   ♦ If the remainder is 2, the result is -1
   ♦ If the remainder is 3, the result is -i
• Let us see an example:
Find the value of $i^{15}$
Solution:
(i) Dividing 15 by 4, we get: $\frac{15}{4}=3\frac{3}{4}$
   ♦ So the remainder is 3
   ♦ Thus we get: $i^{15}=-i$
(ii) Check:
$i^{15}=\left(i^{14}\right)i=\left(i^{2}\right)^7i=\left(-1\right)^7 i=\left[(-1)^6 × -1 \right]i=\left[\left(-1^2\right)^3 × -1 \right]i$

${}=\left[\left(1\right)^3 × -1 \right]i=\left[1 × -1 \right]i=\left[-1 \right]i=-i$

◼ Next we will consider negative powers.
Negative powers can be converted into positive powers by taking the reciprocals. Once the powers become positive, we can use the above method.
• Let us see an example:
Find the value of $i^{-18}$
Solution:
(i) $i^{-18}= \frac{1}{i^{18}}$
(ii) Dividing 18 by 4, we get: $\frac{18}{4}=4\frac{2}{4}$
   ♦ So the remainder is 2
   ♦ Thus we get: $i^{-18}= \frac{1}{i^{18}}=\frac{1}{-1}=-1$
(iii) Check:
$i^{-18}= \left[ i^{-1}\right]^{18}=(-i)^{18}=(-1)^{18}(i)^{18}=(1)(i)^{18}$

${}=i^{18}=\left(i^{2}\right)^9=\left(-1\right)^9=-1$

F. The square roots of negative real numbers
• In the first section of this chapter, we derived the result:
If '$a$' is a positive real number, $\sqrt{-a}=\sqrt{a} × \sqrt{-1}=\sqrt{a}\,i$
• Using this result, we can write the square root of any real number.
• However, there is a possible contradiction when we take the square root of the product of two -ve real numbers. This can be explained in 2 steps:
1. We know that, $\sqrt{a} × \sqrt{b}=\sqrt{ab}$
• This result is applicable when:
   ♦ Both a and b are greater than zero.
   ♦ a is greater than 0 but b is less than zero.
         ✰ $\sqrt{a} × \sqrt{-b}=\sqrt{a} × \sqrt{b}\,i = \sqrt{ab}\,i$
   ♦ b is greater than 0 but a is less than zero.
         ✰ $\sqrt{-a} × \sqrt{b}=\sqrt{a}\,i × \sqrt{b} = \sqrt{ab}\,i$
2. What happens if both a and b are less than zero?
Answer: If both are less than zero, it is possible to write as:
$\sqrt{-a} × \sqrt{-b}=\sqrt{a}\,i × \sqrt{b}\,i = \sqrt{ab} × i^2 =\sqrt{ab} × -1 =-\sqrt{ab}$
• But the square root of the product of two -ve real numbers is never negative. So there is a contradiction.
• Based on this, mathematicians have decided that:
The formula $\sqrt{a} × \sqrt{b}=\sqrt{ab}$ is not applicable when both a and b are less than zero.

G. Identities related to complex numbers.
• Identities help us to perform algebraic operations quickly. Some important identities related to complex numbers are given below:
1. $(z_1+z_2)^2=z_1^2 +2z_1 z_2 + z_2^2 $
• Let us write the proof:
$\begin{array}{ll}
(z_1+z_2)^2&{}={}& (z_1+z_2) × (z_1+z_2)& {} &{} \\
\phantom{(z_1+z_2)^2}&{}={}& (z_1+z_2)z_1~+~(z_1+z_2)z_2 &\color {green}{\text{Distributive law}} &{} \\
\phantom{(z_1+z_2)^2}&{}={}& z_1^2+z_2z_1+z_1z_2+z_2^2 &\color {green}{\text{Distributive law}} &{} \\
\phantom{(z_1+z_2)^2}&{}={}& z_1^2+z_1z_2+z_1z_2+z_2^2 &\color {green}{\text{Commutative law}} &{} \\
\phantom{(z_1+z_2)^2}&{}={}& z_1^2+2z_1z_2+z_2^2 &{} &{} \\
\end{array}$
• Two points can be written about this identity:
(i) We know how to multiply two complex numbers z₁ and z₂
• If z₁ = (a+bi) and z₂ = (c+di), then:
z₁z₂ = (ac-bd)+(ad+bc)i
• So the second term in the above identity can be easily calculated.
(ii) z₁² and/or z₂² can be calculated in a similar way:
$\begin{array}{ll}
(a+bi)(c+di)&{}={}& (ac-bd)~+~(ad+bc)i  & {} \\
(a+bi)(a+bi)&{}={}& a×a~-~b×b~+~(a×b~+~b×a)i &\color {green}{\text{Put c = a and d = b}} & {} \\
\Rightarrow (a+bi)^2 &{}={}& a^2~-~b^2~+~(ab+ba)i&{} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& a^2~-~b^2~+~(ab+ab)i&{} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& \left(a^2-b^2\right)+(2ab)i&{} & {} \\
\end{array}$
2. $(z_1-z_2)^2=z_1^2 -2z_1 z_2 + z_2^2 $

3. $(z_1+z_2)^3=z_1^3 +3z_1^2 z_2+3z_1 z_2^2 + z_2^3 $

4. $(z_1-z_2)^3=z_1^3 -3z_1^2 z_2+3z_1 z_2^2 - z_2^3 $

5. $z_1^2-z_2^2=(z_1+z_2)(z_1-z_2)$

• Identities (2) to (5) above can be proved using methods similar to that we used for (1).

---

Now we will see some solved examples.
Solved example 5.1
Express the following in the form a+bi
(i) $(-5i)\left(\frac{1}{8}i\right)$  (ii) $(-i)(2i)\left(\frac{1}{8}i\right)^3$
Solution (i):
$\begin{array}{ll}
(-5i)\left(\frac{1}{8}i\right)&{}={}& -1 × 5 × i × \frac{1}{8} × i& {} &{} \\
\phantom{(-5i)\left(\frac{1}{8}i\right)}&{}={}& -1 × 5 × \frac{1}{8} × i^2 &{} \\
\phantom{(-5i)\left(\frac{1}{8}i\right)}&{}={}& -1 × 5 × \frac{1}{8} × -1 &{} \\
\phantom{(-5i)\left(\frac{1}{8}i\right)}&{}={}& \frac{5}{8} &{} \\
\phantom{(-5i)\left(\frac{1}{8}i\right)}&{}={}& \frac{5}{8}+0i &{} \\
\end{array}$

Solution (ii):
$\begin{array}{ll}
(-i)(2i)\left(\frac{1}{8}i\right)^3&{}={}& -1 × i × 2 × i × (-1)^3 × \frac{1}{8^3} × i^3& {} &{} \\
\phantom{(-i)(2i)\left(\frac{1}{8}i\right)^3}&{}={}& -1 × 2 × (-1)^3 × \frac{1}{8^3} × i^5 &{} \\
\phantom{(-i)(2i)\left(\frac{1}{8}i\right)^3}&{}={}& -1 × 2 × -1 × \frac{1}{8^3} × i &{} \\
\phantom{(-i)(2i)\left(\frac{1}{8}i\right)^3}&{}&\color {green}{5\div4=1 \frac{1}{4}\text{    Remainder is 1. So }i^5=i} &{} \\
\phantom{(-i)(2i)\left(\frac{1}{8}i\right)^3}&{}={}& 2 × \frac{1}{(2^3)^3} × i &{} \\
\phantom{(-i)(2i)\left(\frac{1}{8}i\right)^3}&{}={}& 2 × \frac{1}{2^9} × i &{} \\
\phantom{(-i)(2i)\left(\frac{1}{8}i\right)^3}&{}={}& \frac{1}{2^8} × i &{} \\
\phantom{(-i)(2i)\left(\frac{1}{8}i\right)^3}&{}={}& \frac{1}{256}i &{} \\
\end{array}$

Solved example 5.2
Express (5-3i)³ in the form a+bi
Solution:
We can use the identity: $(z_1-z_2)^3=z_1^3 -3z_1^2 z_2+3z_1 z_2^2 - z_2^3 $
$\begin{array}{ll}
(5-3i)^3&{}={}&5^3~-~3 × 5^2 × (3i)~+~3 × 5 × (3i)^2~-~ (3i)^3 & {} &{} \\
\phantom{(5-3i)^3}&{}={}&125~-~75 × (3i)~+~15 × 3^2 × i^2~-~ 3^3 × i^3 &{} \\
\phantom{(5-3i)^3}&{}={}&125~-~225i~+~135 × i^2~-~ 27 × i^3 &{} \\
\phantom{(5-3i)^3}&{}={}&125~-~225i~+~135 × -1~-~ 27 × (-i) &{} \\
\phantom{(5-3i)^3}&{}={}&125~-~225i~+~-135~-~ -27i &{} \\
\phantom{(5-3i)^3}&{}={}&125~-135~-~225i~+27i &{} \\
\phantom{(5-3i)^3}&{}={}&-10-198i &{} \\
\end{array}$

Solved example 5.3
Express $(-\sqrt{3}+\sqrt{-2})(2\sqrt{3}-i)$ in the form a+bi
Solution:
$\begin{array}{ll}
(-\sqrt{3}+\sqrt{-2})(2\sqrt{3}-i)&{}={}&(-\sqrt{3}+\sqrt{2}\,i)(2\sqrt{3}-i)& {} &{} \\
\phantom{(-\sqrt{3}+\sqrt{-2})(2\sqrt{3}-i)}&{}&\color {green}{\because~\sqrt{-2}=\sqrt{2}\,i} &{} \\
\phantom{(-\sqrt{3}+\sqrt{-2})(2\sqrt{3}-i)}&{}={}&[(-\sqrt{3} × 2\sqrt{3})-(\sqrt{2} × -1)]~+~[(-\sqrt{3} × -1)+(\sqrt{2} × 2\sqrt{3})]i &{} \\
\phantom{(-\sqrt{3}+\sqrt{-2})(2\sqrt{3}-i)}&{}&\color {green}{\because~(a+bi)(c+di)=(ac-bd)~+~(ad+bc)i} &{} \\
\phantom{(-\sqrt{3}+\sqrt{-2})(2\sqrt{3}-i)}&{}={}&[(-2(\sqrt{3})^2)--(\sqrt{2})]~+~[(\sqrt{3})+(2\sqrt{2}×\sqrt{3})]i &{} \\
\phantom{(-\sqrt{3}+\sqrt{-2})(2\sqrt{3}-i)}&{}={}&[(-2 × 3)+\sqrt{2}]~+~[(\sqrt{3})i+(2\sqrt{2}×\sqrt{3})i] &{} \\
\phantom{(-\sqrt{3}+\sqrt{-2})(2\sqrt{3}-i)}&{}={}&[-6+\sqrt{2}]~+~[\sqrt{3}\,i+(2\sqrt{2}×\sqrt{3}) × i] &{} \\
\phantom{(-\sqrt{3}+\sqrt{-2})(2\sqrt{3}-i)}&{}={}&(-6+\sqrt{2})+\sqrt{3}(1+2\sqrt{2})i &{} \\
\end{array}$

---

• So we have completed a discussion on the algebra of complex numbers.
• In the next section, we will see Modulus and conjugate of a complex number.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 5.1 - Complex Numbers And Their Algebra

In the previous section, we saw how square root of -ve numbers can be denoted using the symbol i. In this section, we will see complex numbers.

Complex numbers

Some basics about complex numbers can be written in 6 steps:
1. Consider the formula for finding the solutions of quadratic equation:
$x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
• In some cases, b²-4ac may work out to a number less than zero. In such cases, we used to wind up the calculations saying that 'there are no real solutions'.
2. But now we have a method to proceed with the calculations along an alternate path.
• Suppose that, we have the quadratic equation: $2x^2 + 3x + \frac{7}{4}$
    ♦ Here a = 2, b = 3 and c = 7/4
• Then we get:
$\begin{array}{ll}
b^2 - 4ac~=& 3^2 - 4 × 2 × \frac{7}{4} & {} & {} & {} \\
\phantom{b^2 - 4ac}~=&9 - 14 & {} &{} & {} \\
\phantom{b^2 - 4ac}~=& - 5 & {} &{} & {} \\
\end{array}$
3.Applying the formula, we get: $x=\frac{-3 \pm \sqrt{-5}}{4}$
• The right side can be split into two parts: $-\frac{3}{4}~\pm~\frac{\sqrt{-5}}{4}$
• We used to wind up the calculations due to the presence of '-5'.
• But now, based on what we have discussed in the previous section, we can write the right side as: $-\frac{3}{4}~\pm~\frac{\sqrt{5}i}{4}$
• So the solutions are: $-\frac{3}{4}~+~\frac{\sqrt{5}i}{4}$ and $-\frac{3}{4}~-~\frac{\sqrt{5}i}{4}$
4. A number of the form $a+bi$ is defined to be a complex number.
◼ ‘a’ and ‘b’ should be real numbers
• Some examples are:
    ♦ $3+5i$  
    ♦ $-2+ \sqrt{7}i$  
    ♦ $5+ \left(\frac{-3}{11} \right)i$  
5. Consider a complex number $z=a+bi$
    ♦ ‘a’ is called the real part. It is denoted by Re z
    ♦ ‘b’ is called the imaginary part. It is denoted by Im z 
• Let us see an example: If $z=3+7i$, then:
   ♦ Re z = 3
   ♦ Im z = 7
• For our present case of $-\frac{3}{4}~+~\frac{\sqrt{5}i}{4}$,
    ♦ Re z = $-\frac{3}{4}$
    ♦ Im z = $\frac{\sqrt{5}}{4}$
• For our present case of $-\frac{3}{4}~-~\frac{\sqrt{5}i}{4}$,
    ♦ Re z = $-\frac{3}{4}$
    ♦ Im z = $-\frac{\sqrt{5}}{4}$
6. Consider two complex numbers:
z₁ = a+bi and z₂ = c+di
• z₁ will be equal to z₂ if two conditions are satisfied:
    ♦ a = c
    ♦ b = d
• Let us see an example:
Given that the two complex numbers [(2x+3y) + 25i] and [20 + (3x+2y)i] are equal. If x and y are real numbers, find the actual values of x and y.
Solution:
• Given that the two complex numbers are equal. So we can equate the corresponding parts.
    ♦ Equating the real parts, we get: 2x+3y = 20
    ♦ Equating the imaginary parts, we get: 25 = 3x+2y
• So we have two simultaneous equations in two variables:
    ♦ 2x+3y = 20
    ♦ 3x+2y = 25
• They can be solved as follows:
$\begin{array}{ll}
2x+3y&{}={}& 20 & \color {green}{\text{- - - - (a)}} & {} \\
3x+2y&{}={}& 25 & \color {green}{\text{- - - - (b)}} & {} \\
6x+9y&{}={}& 60 & \color {green}{\text{- - - - (c)}} & \color {green}{\text{[Multiplying (a) by 3]}} \\
6x+4y&{}={}& 50 & \color {green}{\text{- - - - (d)}} & \color {green}{\text{[Multiplying (b) by 2]}} \\
5y&{}={}& 10 & {} & \color {green}{\text{[(c) - (d)]}} \\
\Rightarrow ~y&{}={}& 2 & {} & {} \\
2x+6&{}={}& 20 & {} & \color {green}{\text{[Substituting for y in (a)]}} \\
\Rightarrow ~x&{}={}& 7 & {} & {} \\
\end{array}$
• Thus we get: x = 7 and y = 2

Algebra of Complex Numbers

• Consider the quadratic equation that we saw in step (2) above. Let us write it again: $2x^2 + 3x + \frac{7}{4}$
    ♦ We saw that, it’s solutions are complex numbers:
        ✰ $-\frac{3}{4}~+~\frac{\sqrt{5}i}{4}$
        ✰ $-\frac{3}{4}~-~\frac{\sqrt{5}i}{4}$
• We will want to check whether those complex numbers indeed are the solutions.
• For that, we will want to input each of them into the original quadratic equation. We will be writing thus:
(i) Checking whether $-\frac{3}{4}~+~\frac{\sqrt{5}i}{4}$ is a solution:
$$2\left(-\frac{3}{4}~+~\frac{\sqrt{5}i}{4} \right)^2 + 3\left(-\frac{3}{4}~+~\frac{\sqrt{5}i}{4} \right) + \frac{7}{4}=0$$
(ii) Checking whether $-\frac{3}{4}~-~\frac{\sqrt{5}i}{4}$ is a solution:
$$2\left(-\frac{3}{4}~-~\frac{\sqrt{5}i}{4} \right)^2 + 3\left(-\frac{3}{4}~-~\frac{\sqrt{5}i}{4} \right) + \frac{7}{4}=0$$
• Consider (i):
In the first term, we squared the complex number. In the second term, we multiplied the complex number by a constant 3
• Consider (ii):
Here also, in the first term, we squared the complex number. In the second term, we multiplied the complex number by a constant 3
• In the same way, we may want to:
    ♦ Add two complex numbers.
    ♦ Subtract a complex number from another complex number.
    ♦ Multiply two complex numbers.
    ♦ Divide a complex number by another complex number.
• In short, we may want to perform various algebraic operations on complex numbers. So we must have a good knowledge on performing such operations.

A. Addition of two complex numbers
This can be written in 6 steps:
1. If z₁ = a+bi and z₂ = c+di, then z₁+z₂ is defined as:
z₁+z₂ = (a+c)+(b+d)i
• That is:
    ♦ Real parts are added together.
    ♦ Imaginary parts are added together.
• Let us see an example:
    ♦ (4+7i)+(-3+11i) = (4-3)+(7+11)i = 1+18i
• Note that, sum is also a complex number.
2. The addition of complex numbers satisfy the closure law.
• According to this law, the sum of two complex numbers is a complex number.
• That is:
For any two complex numbers z₁ and z₂, the sum (z₁+z₂) will be a complex number.
3. Addition of two complex numbers satisfy the commutative law.
• That is:
For any two complex numbers z₁ and z₂, (z₁+z₂) = (z₂+z₁).
4. Addition of two complex numbers satisfy the associative law.
• That is:
For any three complex numbers z₁, z₂ and z₃, (z₁+z₂)+z₃ =  z₁+(z₂+z₃).
5. Any complex number z added to (0+0i) will give the same z.
• That is:
z+(0+0i) = z
• This property is called existence of additive identity.
    ♦ The complex number (0+0i) is called the additive identity.
    ♦ It is also called zero complex number.
    ♦ It is denoted as 0
6. Any complex number z = a+bi added to [-a+(-b)i] will give a zero complex number.
• That is:
a+bi + [-a+(-b)i] = (a-a)+(b-b)i = 0+0i
• This property is called existence of additive inverse.
    ♦ The complex number [-a+(-b)i] is called the additive inverse.
    ♦ It is also called negative of z.
    ♦ If a complex number is denoted as z, it’s additive inverse is denoted as -z.
• The sum of any complex number and it’s additive inverse will always be a zero complex number.

B. Difference of two complex numbers.
This can be written as follows:
1. If z₁ = a+bi and z₂ = c+di, then the difference z₁-z₂ is defined as:
z₁-z₂ = z₁+(-z₂) = a+bi+[-c+(-d)i] = (a-c)+(b-d)i
• That is:
    ♦ We add the additive inverse of z₂ to z₁.
• Let us see two examples:
    ♦ (4+7i)-(-3+11i) = (4+7i)+[3+(-11)i] = (4+3)+(7-11)i = 7-4i
    ♦ (2-3i)-(6+9i) = (2-3i)+[-6+(-9)i] = (2-6)+(-3-9)i = -4-12i
• Note that, difference is also a complex number.

C. Multiplication of two complex numbers.
This can be written in 7 steps:
1. If z₁ = a+bi and z₂ = c+di, then the product z₁z₂ is defined as:
z₁z₂ = (ac-bd)+(ad+bc)i
• This result can be derived as follows:
$\begin{array}{ll}
(a+bi)(c+di)&{}={}& a × c~+~a × di~+~bi × c~+~bi × di &{} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& ac~+~adi~+~bci~+~bd × i^2 &{} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& ac~+~(ad+bc)i~+~bd × (\sqrt{-1})^2 &{} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& ac~+~(ad+bc)i~+~bd × (-1) &{} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& ac~+~(ad+bc)i~+~(-bd) &{} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& (ac-bd)~+~(ad+bc)i &{} & {} \\
\end{array}$
• Let us see an example:
    ♦ (2+9i)(3+7i) = (2 × 3 - 9 × 7)+(2 × 7 + 9 × 3)i = (6-63)+(14+27)i = -57+41i
2. The multiplication of complex numbers satisfy the closure law.
• According to this law, the product of two complex numbers is a complex number.
• That is:
For any two complex numbers z₁ and z₂, the product z₁z₂ will be a complex number.
3. Multiplication of two complex numbers satisfy the commutative law.
• That is:
For any two complex numbers z₁ and z₂, (z₁z₂) = (z₂z₁).
4. Multiplication of two complex numbers satisfy the associative law.
• That is:
For any three complex numbers z₁, z₂ and z₃, (z₁z₂)z₃ =  z₁(z₂z₃).
5. Any complex number z multiplied by (1+0i) will give the same z.
• That is:
z × (1+0i) = z
• This property is called existence of multiplicative identity.
    ♦ The complex number (1+0i) is called the multiplicative identity.
    ♦ It is denoted as 1
• The proof can be written as follows:
$\begin{array}{ll}
(a+bi)(c+di)&{}={}& (ac-bd)~+~(ad+bc)i &\color {green}{\text{This is already proved above.}} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& a×1~-~b×0~+~(a×0~+~b×1)i &\color {green}{\text{Put c = 1 and d = 0.}} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& a~-~0~+~(0+b)i&{} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& a+bi&{} & {} \\
\end{array}$
6. Any complex number z = a+bi multiplied by $\left[\frac{a}{a^2+b^2}~+~\left(\frac{-b}{a^2+b^2} \right)i\right]$ will give 1.
(Remember that 1, which actually is the complex number (1+0i), is the multiplicative identity)
• That is:
$(a+bi) × \left[\frac{a}{a^2+b^2}~+~\left(\frac{-b}{a^2+b^2} \right)i \right]~=~1$
• This property is called existence of multiplicative inverse.
    ♦ The complex number $\left[\frac{a}{a^2+b^2}~+~\left(\frac{-b}{a^2+b^2} \right)i \right]$ is called the multiplicative inverse.
    ♦ If a complex number is denoted as $z$, it’s multiplicative inverse is denoted as $\frac{1}{z}$.
• We can write:
If $z=a+bi$, then $\frac{1}{z}=\frac{a}{a^2+b^2}~+~\left(\frac{-b}{a^2+b^2} \right)i$
• The product of any complex number and it’s multiplicative inverse will always be 1. That is: $z × \frac{1}{z}=1$
• The proof can be written as follows:
$\begin{array}{ll}
(a+bi)(c+di)&{}={}& (ac-bd)~+~(ad+bc)i &\color {green}{\text{This is already proved above.}} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& a×\frac{a}{a^2+b^2}~-~b×\frac{-b}{a^2+b^2}~+~\left[a×\frac{-b}{a^2+b^2}~+~b×\frac{a}{a^2+b^2}\right] i &\color {green}{\text{Changing c and d.}} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& \frac{a^2}{a^2+b^2}~+~\frac{b^2}{a^2+b^2}~+~\left[\frac{-ab}{a^2+b^2}~+~\frac{ab}{a^2+b^2}\right] i &{}& {} \\
\phantom{(a+bi)(c+di)}&{}={}& \frac{a^2+b^2}{a^2+b^2}~+~\left[\frac{-ab+ab}{a^2+b^2}\right] i &{}& {} \\
\phantom{(a+bi)(c+di)}&{}={}& 1~+~0i&{} & {} \\
\phantom{(a+bi)(c+di)}&{}={}& 1&{} & {} \\
\end{array}$
◼ For the existence of multiplicative inverse, both a and b should be non-zero real numbers.
7. Multiplication of two complex numbers satisfy the distributive law.
• That is:
For any three complex numbers z₁, z₂ and z₃,
(a) z₁(z₂+z₃) =  z₁z₂ + z₁z₃.
(a) (z₁+z₂)z₃ =  z₁z₃ + z₂z₃.

---

In the next section, we will see more algebraic operations.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 5 - Complex Numbers and Quadratic Equations

In the previous section, we completed a discussion on mathematical induction. In this chapter, we will see complex numbers and quadratic equations.

Let us recall the three types of equations that we have seen in our earlier classes.
(i) Linear equations in one variable
Example:
2x+5 = 17
• We know how to solve such equations. (Details here)
(ii) Linear equations in two variables
Example:
4x+3y = 43
3x - 2y = 11
• We know how to solve such equations. (Details here)  
(iii) Quadratic equations in one variable
Example: x² + 2x – 224 = 0
• We know how to solve such equations. (Details here)

---

• Let us consider the quadratic equations again.
We know that, the solutions of a quadratic equation can be found out by using the equation: $\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
• Consider the portion $b^2 - 4ac$.
If this portion is -ve, we will not be able to calculate $\sqrt{b^2 - 4ac}$.
Because, root of -ve numbers do not exist.
(Mark any point on the number line. Even if that number is -ve, it’s square will be a +ve number. That is why we say that, root of a -ve number is not a real number)
• So in this chapter we try an alternate method to solve quadratic equations, when $b^2 - 4ac$ is -ve.

Significance of i

Some basics about $i$ can be written in 6 steps:
1. Consider the quadratic equation: $x^2 + 1 = 0$   
• Rearranging it, we get: $x^2 = -1$
• So $x = \pm \sqrt{-1}$
2. We know that $\sqrt{-1}$ is not a real number.
• Let us denote $\sqrt{-1}$ by the symbol $i$
• Then we get: $x = \pm i$
• That is: x = $i$ or $-i$
(i) Let us substitute $i$ in the place of x in the given equation. We get: $i^2 +1 = 0$
   ♦ That is., $(\sqrt{-1})^2 + 1 = 0 ~\Rightarrow~ -1 + 1 = 0$, which is true.
   ♦ So we can write: $i$ is a solution of the equation $x^2 + 1 = 0$  
(ii) Let us substitute $-i$ in the place of x in the given equation. We get: $(-i)^2 +1 = 0$
   ♦ That is., $(-\sqrt{-1})^2 + 1 = 0 ~\Rightarrow~ [(-1 × -1) × -1] + 1 = 0$
   ♦ That is.,$[(1) × -1]+1 = 0~\Rightarrow~ -1+1 =0$, which is true.
   ♦ So we can write: $-i$ is also a solution of the equation $x^2 + 1 = 0$  
(iii) Thus we get:
   ♦ Solutions of the equation $x^2 + 1 = 0$ are $\sqrt{-1}$ and $-\sqrt{-1}$
   ♦ In other words:
   ♦ Solutions of the equation $x^2 + 1 = 0$ are $i$ and $-i$

• While solving the equation $x^2 + 1 = 0$, we are actually calculating the square roots of -1. This is clear from the fact that, the equation is rearranged into the form: $x^2 = -1$ • From the detailed steps that we wrote, we come to the conclusion that: $\sqrt{-1}$ can be $i$  or $-i$ • However, when we write $\sqrt{-1}$, we would mean $i$ only.    ♦ If we want $-i$, we must specifically write $-\sqrt{-1}$

3. We denoted $\sqrt{-1}$ by the symbol $i$. What about $\sqrt{-2}$ ?
(i) Consider the quadratic equation: $x^2 + 2 = 0$   
• Rearranging it, we get: $x^2 = -2$
• So $x = \pm \sqrt{-2}$
(ii) We can write $\pm \sqrt{-2}$ as:
$\pm \sqrt{-1 \times 2}~=~\pm \sqrt{-1} \times \sqrt{2}~=~ \pm i \times \sqrt{2}$
• So we get: $\sqrt{-2}~=~\pm \sqrt{2}\,i$  
(iii) Let us substitute $\sqrt{2}\,i$ in the place of x in the given equation. We get: $(\sqrt{2}\,i)^2 +2 = 0$
   ♦ That is., $[(\sqrt{2})^2~ × ~i^2] + 2 = 0$
   ♦ That is., $[(\sqrt{2})^2~ × ~(\sqrt{-1})^2] + 2 = 0 ~\Rightarrow~ [2 × -1] + 2 = 0$, which is true.
   ♦ So we can write: $\sqrt{2}\;i$ is a solution of the equation $x^2 + 2 = 0$  
(iv) Let us substitute $-\sqrt{2}\,i$ in the place of x in the given equation. We get:
$(-\sqrt{2}\,i)^2 +2 = 0$
   ♦ That is., $[(-1 × -1) × ~ (\sqrt{2})^2~ × ~i^2] + 2 = 0$
   ♦ That is., $[(-1 × -1) × ~ (\sqrt{2})^2 × ~(\sqrt{-1})^2] + 2 = 0$
   ♦ That is., $[(1) × 2 × -1] + 2 = 0~\Rightarrow~[-2]+2=0$, which is true.
   ♦ So we can write: $-\sqrt{2}\;i$ is also a solution of the equation $x^2 + 2 = 0$
(v) Thus we get:
   ♦ Solutions of the equation $x^2 + 2 = 0$ are $\sqrt{-2}$ and $-\sqrt{-2}$
   ♦ In other words:
   ♦ Solutions of the equation $x^2 + 2 = 0$ are $\sqrt{2}\;i$ and $-\sqrt{2}\;i$

• While solving the equation $x^2 + 2 = 0$, we are actually calculating the square roots of -2. This is clear from the fact that, the equation is rearranged into the form: $x^2 = -2$ • From the detailed steps that we wrote, we come to the conclusion that: $\sqrt{-2}$ can be $\sqrt{2}\,i$  or $-\sqrt{2}\,i$ • However, when we write $\sqrt{-2}$, we would mean $\sqrt{2}\,i$ only.    ♦ If we want $-\sqrt{2}\,i$, we must specifically write $-\sqrt{-2}$

4. We denoted $\sqrt{-1}$ by the symbol $i$. What about $\sqrt{-3}$ ?
(i) Consider the quadratic equation: $x^2 + 3 = 0$   
• Rearranging it, we get: $x^2 = -3$
• So $x = \pm \sqrt{-3}$
(ii) We can write $\sqrt{-3}$ as:
$\pm \sqrt{-1 \times 3}~=~\pm \sqrt{-1} \times \sqrt{3}~=~ \pm i \times \sqrt{3}$
• So we get: $\sqrt{-3}~=~\pm \sqrt{3} \,i$  
(iii) Let us substitute $\sqrt{3}\,i$ in the place of x in the given equation. We get: $(\sqrt{3}\;i)^2 +3 = 0$
   ♦ That is., $[(\sqrt{3})^2~ × ~i^2] + 3 = 0$
   ♦ That is., $[(\sqrt{3})^2~ × ~(\sqrt{-1})^2] + 3 = 0 ~\Rightarrow~ [3 × -1] + 3 = 0$, which is true.
   ♦ So we can write: $\sqrt{3}\,i$ is a solution of the equation $x^2 + 3 = 0$  
(iv) Let us substitute $-\sqrt{3}\,i$ in the place of x in the given equation. We get:
$(-\sqrt{3}\,i)^2 +3 = 0$
   ♦ That is., $[(-1 × -1) × ~ (\sqrt{3})^2~ × ~i^2] + 3 = 0$
   ♦ That is., $[(-1 × -1) × (\sqrt{3})^2 × (\sqrt{-1})^2] + 3 = 0$
   ♦ That is., $[(1) × 3 × -1] + 3 = 0~\Rightarrow~[-3]+3=0$, which is true.
   ♦ So we can write: $-\sqrt{3}\,i$ is also a solution of the equation $x^2 + 3 = 0$
(v) Thus we get:
   ♦ Solutions of the equation $x^2 + 3 = 0$ are $\sqrt{-3}$ and $-\sqrt{-3}$
   ♦ In other words:
   ♦ Solutions of the equation $x^2 + 3 = 0$ are $\sqrt{3}\,i$ and $-\sqrt{3}\,i$

• While solving the equation $x^2 + 3 = 0$, we are actually calculating the square roots of -3. This is clear from the fact that, the equation is rearranged into the form: $x^2 = -3$ • From the detailed steps that we wrote, we come to the conclusion that: $\sqrt{-3}$ can be $\sqrt{3}\,i$  or $-\sqrt{3}\,i$ • However, when we write $\sqrt{-3}$, we would mean $\sqrt{3}\,i$ only.    ♦ If we want $-\sqrt{3}\,i$, we must specifically write $-\sqrt{-3}$

5. We denoted $\sqrt{-1}$ by the symbol $i$. What about $\sqrt{-4}$ ?
(i) Consider the quadratic equation: $x^2 + 4 = 0$   
• Rearranging it, we get: $x^2 = -4$
• So $x = \pm \sqrt{-4}$
(ii) We can write $\pm \sqrt{-4}$ as:
$\pm \sqrt{-1 \times 4}~=~\pm \sqrt{-1} \times \sqrt{4}~=~ \pm i \times \sqrt{4}$
• So we get: $\sqrt{-4}~=~\pm \sqrt{4}\,i~=~\pm 2i$  
(iii) Let us substitute $2i$ in the place of x in the given equation. We get: $(2i)^2 +4 = 0$
   ♦ That is., $[(2)^2~ × ~i^2] + 4 = 0$
   ♦ That is., $[(2)^2~ × ~(\sqrt{-1})^2] + 4 = 0 ~\Rightarrow~ [4 × -1] + 4 = 0$, which is true.
   ♦ So we can write: $2i$ is a solution of the equation $x^2 + 4 = 0$  
(iv) Let us substitute $-2i$ in the place of x in the given equation. We get:
$(-2i)^2 +4 = 0$
   ♦ That is., $[(-1 × -1) × ~ (2)^2~ × ~i^2] + 4 = 0$
   ♦ That is., $[(-1 × -1) × (2)^2~ × ~(\sqrt{-1})^2] + 4 = 0$
   ♦ That is., $[(1) × 4 × -1] + 4 = 0~\Rightarrow~[-4]+4=0$, which is true.
   ♦ So we can write: $-2i$ is also a solution of the equation $x^2 + 4 = 0$
(v) Thus we get:
   ♦ Solutions of the equation $x^2 + 4 = 0$ are $\sqrt{-4}$ and $-\sqrt{-4}$
   ♦ In other words:
   ♦ Solutions of the equation $x^2 + 4 = 0$ are $2i$ and $-2i$

• While solving the equation $x^2 + 4 = 0$, we are actually calculating the square roots of -4. This is clear from the fact that, the equation is rearranged into the form: $x^2 = -4$ • From the detailed steps that we wrote, we come to the conclusion that: $\sqrt{-4}$ can be $2i$  or $-2i$ • However, when we write $\sqrt{-4}$, we would mean $2i$ only.    ♦ If we want $-2i$, we must specifically write $-\sqrt{-4}$

6. In this way, we can write the square roots of -5, -6, -7, . . . so on.
• In fact, we can write the square roots of any -ve real number.
• Generally, if '$a$' is a positive real number, $\sqrt{-a}=\sqrt{a} × \sqrt{-1}=\sqrt{a}\,i$

---

• So now we know the significance of $i$.
• Using $i$, we can do problems involving the square roots of -ve real numbers. We will see those problems in later sections.
• In the next section, we will see complex numbers.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com