Chapter 12.6 - Miscellaneous Examples

In the previous section, we saw some solved examples on section formula. In this section, we will see some miscellaneous examples.

Solved example 12.11
Show that the points A(1,2,3), B(-1,-2,-1), C(2,3,2) and D(4,7,6) are the vertices of a parallelogram ABCD but it is not a rectangle.
Solution:
1. A rough sketch is shown in fig.12.19 below:

Fig.12.19

2. Using the distance formula, we can find the lengths of sides.
   ♦ AB = √36 = 6
   ♦ BC = √43
   ♦ CD = √36 = 6
   ♦ DA = √43
3. We see that, both pairs of opposite sides (AB, CD) and (BC, DA) are equal. So it is a parallelogram.
4. A rectangle is a parallelogram in which both diagonals are of the same length.
• If a parallelogram is not to be a rectangle, it's diagonals should not be of the same length.
5. Using distance formula, let us write the lengths of the diagonals:
   ♦ AC = √3
   ♦ BD = √155
• We see that, diagonals are not equal. So it a parallelogram which is not a rectangle.

Solved example 12.12
Find the equation of the set of points P such that it's distances from the points A(3,4,-5) and B(-2,1,4) are equal.
Solution:
1. Let P(x,y,z) be equidistant from A and B
2. Let us use the distance formula.
• Square of the distance PA can be obtained as follows:
PA² = (x-3)² + (y-4)² + (z+5)²
= x² -6x +9 +y² -8y +16 +z² +10z +25
• Square of the distance PB can be obtained as follows:
PB² = (x+2)² + (y-1)² + (z-4)²
= x² +4x +4 +y² -2y +1 +z² -8z +16
3. Since the distances are equal, the square of the distances will also be equal. We can write:
x² -6x +9 +y² -8y +16 +z² +10z +25 = x² +4x +4 +y² -2y +1 +z² -8z +16
⇒ -6x +9 -8y +16 +10z +25 = +4x +4 -2y +1 -8z +16
⇒ -6x -4x +9 -8y +2y +16 +10z +8z +25 = +4  +1 +16
⇒ -10x +9 -6y +16 +18z +25 = +4  +1 +16
⇒ -10x -6y +18z +50 = 21
⇒ -10x -6y +18z +29 = 0
⇒ 10x +6y -18z -29 = 0

Solved example 12.13
The centroid of a triangle ABC is at G(1,1,1). If the coordinates of A and B are (3,-5,7) and (-1,7,-6) respectively, find the coordinates of C.
Solution:
1. Let the coordinates of C be (x,y,z)
Then we can draw a rough sketch as shown below:

Fig.12.20

2. We know that, the coordinates of the centroid of any triangle can be obtained using the expression:
$\left( \frac{x_1 + x_2 + x_3}{3},~ \frac{y_1 + y_2 + y_3}{3},~ \frac{z_1 + z_2 + z_3}{3}\right)$  

3. Substituting the known values, we get:
• $ \frac{3 -1 + x}{3}~=~1$
⇒ 2+x = 3
⇒ x = 1 
• $ \frac{-5 +7 + y}{3}~=~1$
⇒ 2+y = 3
⇒ y = 1 
• $ \frac{7 -6 + z}{3}~=~1$
⇒ 1+x = 3
⇒ z = 2

4. So the coordinates of C are: (1,1,2)

---

The link below gives a few more solved examples:

Miscellaneous Exercise

---

We have completed a disscusion on three dimensional geometry. In the next chapter, we will see limits and derivatives.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 12.5 - Solved Examples on Section Formula

In the previous section, we saw section formula. We also saw a solved example. In this section, we will see a few more solved examples.

Solved example 12.8
Using the section formula, prove that the three points A(-4,6,10), B(2,4,6) and C(14,0,-2) are collinear.
Solution:
1. Let us assume that, the third point C is collinear with A and B. Then two possibilities arise:
(i) C lies between A and B
(ii) C lies in the extension of AB
2. If the case is 1(i), then C will be dividing AB internally in some ratio k:1
3. If the case is 1(ii), then C will be dividing AB externally in some ratio k:1
4. For a point which divides AB (internally or externally) in the ratio k:1, the coordinates will be:
$\left(\frac{k x_2 + x_1}{1+k},~\frac{k y_2 + y_1}{1+k},~\frac{k z_2 + z_1}{1+k} \right)$
⇒ $\left(\frac{k × 2 + -4}{1+k},~\frac{k × 4 + 6}{1+k},~\frac{k × 6 + 10}{1+k} \right)$
⇒ $\left(\frac{2k - 4}{1+k},~\frac{4k + 6}{1+k},~\frac{6k + 10}{1+k} \right)$
5. Let us check whether the coordinates of C satisfy the conditions in (4).
The check can be done in 4 steps:
(i) Equating the x coordinates, we get:

$\begin{array}{ll}
{}&{\frac{2k - 4}{1+k}}
& {~=~}& {14}
&{} \\

{\Rightarrow}&{2k-4}
& {~=~}& {14 +14k }
&{} \\

{\Rightarrow}&{-12k}
& {~=~}& {18}
&{} \\

{\Rightarrow}&{-2k}
& {~=~}& {3}
&{} \\

{\Rightarrow}&{k}
& {~=~}& {- \frac{3}{2}}
&{} \\

\end{array}$

(ii) If k = -3/2, then the y-coordinate can be calculated from the result in (4). We get:

$\begin{array}{ll}
{}&{\rm{y-coordinate}}
& {~=~}& {\frac{4k + 6}{1+k}}
&{} \\

{}&{}
& {~=~}& {\frac{4(-3/2) + 6}{1+(-3/2)}}
&{} \\

{}&{}
& {~=~}& {\frac{-6+6}{1+(-3/2)}}
&{} \\

{}&{}
& {~=~}& {0}
&{} \\

\end{array}$

• Note that, the y-coordinate of C is also '0'.

(iii) If k = -3/2, then the z-coordinate can be calculated from the result in (4). We get:

$\begin{array}{ll}
{}&{\rm{z-coordinate}}
& {~=~}& {\frac{6k + 10}{1+k}}
&{} \\

{}&{}
& {~=~}& {\frac{6(-3/2) + 10}{1+(-3/2)}}
&{} \\

{}&{}
& {~=~}& {\frac{-9+10}{-(1/2)}}
&{} \\

{}&{}
& {~=~}& {\frac{1}{-(1/2)}}
&{} \\

{}&{}
& {~=~}& {-2}
&{} \\

\end{array}$

• Note that, the z-coordinate of C is also '-2'.

(iv) So the coordinates of C satisfy the conditions in (4).

6. That means, the point C indeed divides AB internally or externally in the ratio k:1
Since k (= -3/2) is a -ve value, it is an external division.
7. Point C can divide AB (internally or externally) only if A, B and C is collinear.

Solved example 12.9
Find the coordinates of the centroid of the triangle PQR whose vertices are P(x₁,y₁,z₁), Q(x₂,y₂,z₂), R(x₃,y₃,z₃).
Solution:
1. Let A be the midpoint of QR. Then the coordinates of A will be:
$\left(\frac{x_2 + x_3}{2},~\frac{y_2 + y_3}{2},~\frac{z_2 + z_3}{2} \right)$
2. Let G be the centroid.
3. We have the coordinates of P and A.
• The centroid G will divide PA internally in the ratio 2:1
• So the coordinates of G will be:
$\left(\frac{m x_2 + n x_1}{m+n},~\frac{m y_2 + n y_1}{m+n},~\frac{m z_2 + n z_1}{m+n} \right)$
⇒ $\left(\frac{2 × \frac{x_2 + x_3}{2} + 1 × x_1}{2+1},~\frac{2 × \frac{y_2 + y_3}{2} + 1 × y_1}{2+1},~\frac{2 × \frac{z_2 + z_3}{2} + 1 × z_1}{2+1} \right)$
⇒ $\left(\frac{x_2 + x_3 + 1 × x_1}{2+1},~\frac{y_2 + y_3 + 1 × y_1}{2+1},~\frac{z_2 + z_3 + 1 × z_1}{2+1} \right)$
⇒ $\left(\frac{x_1 + x_2 + x_3}{3},~\frac{y_1 + y_2 + y_3}{3},~\frac{z_1 + z_2 + z_3}{3} \right)$

Solved example 12.10
Find the ratio in which the line segment joining the points A(4,8,10) and B(6,10,-8) is divided by the YZ-plane. Also find the coordinates of the point at which the division is done.
Solution:
1. Let the YZ-plane divide AB in the ratio k:1
2. Let the point of division be C.
3. We can write the coordinates of C as follows:
$\left(\frac{k x_2 + x_1}{1+k},~\frac{k y_2 + y_1}{1+k},~\frac{k z_2 + z_1}{1+k} \right)$
⇒ $\left(\frac{k × 6 + 4}{1+k},~\frac{k × 10 + 8}{1+k},~\frac{k × -8 + 10}{1+k} \right)$
⇒ $\left(\frac{6k + 4}{1+k},~\frac{10k + 8}{1+k},~\frac{-8k + 10}{1+k} \right)$
4. Consider any point on the YZ-plane. The x-coordinate of that point will be zero.
So the x-coordinate written in (3) is zero. We get:

$\begin{array}{ll}
{}&{\frac{6k + 4}{1+k}}
& {~=~}& {0}
&{} \\

{\Rightarrow}&{6k + 4}
& {~=~}& {0}
&{} \\

{\Rightarrow}&{6k}
& {~=~}& {-4}
&{} \\

{\Rightarrow}&{3k}
& {~=~}& {-2}
&{} \\

{\Rightarrow}&{k}
& {~=~}& {- \frac{2}{3}}
&{} \\

\end{array}$

5. Thus we get the value of k.
• We have seen that, k:1 is just another form of m:n. Both represent the same ratio.
So we can write:

$\begin{array}{ll}
{}&{k:1}
& {~=~}& {\frac{k}{1}}
&{} \\

{\Rightarrow}&{\frac{k}{1}}
& {~=~}& {\frac{m}{n}}
&{} \\

{\Rightarrow}&{\frac{-(2/3)}{1}}
& {~=~}& {\frac{m}{n}}
&{} \\

{\Rightarrow}&{-\frac{2}{3}}
& {~=~}& {\frac{m}{n}}
&{} \\

\end{array}$

• That means, the YZ-plane divides AB in the ratio m:n where m/n = -(2/3)

6. Now we can calculate the y-coordinate of C.
• Substituting the value of k in the expression for y-coordinate in (3), we get:

$\begin{array}{ll}
{}&{\rm{y-coordinate}}
& {~=~}& {\frac{10k + 8}{1+k}}
&{} \\

{}&{}
& {~=~}& {\frac{10(-2/3) + 8}{1+(-2/3)}}
&{} \\

{}&{}
& {~=~}& {\frac{-20+24}{3-2}}
&{} \\

{}&{}
& {~=~}& {4}
&{} \\

\end{array}$

7. Finally we can calculate the z-coordinate of C.
• Substituting the value of k in the expression for z-coordinate in (3), we get:

$\begin{array}{ll}
{}&{\rm{z-coordinate}}
& {~=~}& {\frac{-8k + 10}{1+k}}
&{} \\

{}&{}
& {~=~}& {\frac{-8(-2/3) + 10}{1+(-2/3)}}
&{} \\

{}&{}
& {~=~}& {\frac{16+30}{3-2}}
&{} \\

{}&{}
& {~=~}& {46}
&{} \\

\end{array}$

8. So the division is done at C(0,4,46)
• Fig.12.18 below shows the actual plot.

Fig.12.18

We can write 3 points:
(i) We see that:
• The YZ-plane does not divide AB
• But the YZ plane divides the extension of AB. So it is an external division. The division is done at C(0,4,46)
(ii) We have the coordinates of all three points:
A(4,8,10), B(6,10,-8) and C(0,4,46)
    ♦ Using the distance formula, BC = √2988
    ♦ Using the distance formula, AC = √1328
(iii) So we get:
$\frac{AC}{BC}~=~\frac{\sqrt{1328}}{\sqrt{2988}}~=~\sqrt{\frac{1328}{2988}}~=~\sqrt{\frac{4}{9}}~=~\frac{2}{3}$

---

The link below gives a few more solved examples:

Exercise 12.3

---

In the next section, we will see some miscellaneous examples.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 12.4 - Section Formula

In the previous section, we completed a discussion on distance formula. In this section, we will see section formula.

• In our earlier classes, we have seen the application of section formula in two-dimensional problems.
• Let us recall the important points related to the section formula. It can be written in 2 steps:
1. In fig.12.13 (a) below, the line segment PQ lies in the XY-plane.    
    ♦ Point R lies between P and Q.
    ♦ Point R divides the segment PQ internally in the ratio m:n
    ♦ Coordinates of P and Q are (x₁,y₁) and (x₂,y₂) respectively.
• Then the coordinates of R will be: $\left(\frac{m x_2 + n x_1}{m+n}, \frac{m y_2 + n y_1}{m+n} \right)$.

Fig.12.13

2. In fig.12.13 (b) above, the line segment PQ lies in the XY-plane.    
    ♦ Point R does not lie between P and Q. It is on the extension of the line PQ.
    ♦ Point R divides the segment PQ externally in the ratio m:n
    ♦ Coordinates of P and Q are (x₁,y₁) and (x₂,y₂) respectively.
• Then the coordinates of R will be:$\left(\frac{m x_2 - n x_1}{m-n}, \frac{m y_2 - n y_1}{m-n} \right)$.

---

• Now we will see the section formula when P(x₁,y₁,z₁) and Q(x₂,y₂,z₂) are two points in three-dimensional space.
    ♦ R (x,y,z) divides PQ in the ratio m:n.
    ♦ We need to derive expressions for x, y and z.
• First, we will derive an expression for z. It can be derived in 8 steps:

1. The first step is to drop perpendiculars from P, Q and R, on to the XY-plane.
• In fig.12.14 below, the XY-plane is shown in blue color.
    ♦ L is the foot of the perpendicular from P.
    ♦ M is the foot of the perpendicular from Q.
    ♦ N is the foot of the perpendicular from R.

Fig.12.14

2. Draw the line LM.
    ♦ Point N will lie on LM.
3. Through R, draw a line parallel to LM.
    ♦ Let this line meet PL (actually, it is the ‘extension of PL’) at S.
    ♦ Let this line meet QM at T.
4. The points P, Q, R, S and T are on the same plane. So we can show them separately as in fig.12.15 below:

Fig.12.15

• Consider the two triangles ΔPRS and ΔQRT.
• Let us analyze the angles of the two triangles. The analysis can be written in 5 steps:
(i) PS and QT are vertical lines because, they are drawn perpendicular to the XY-plane.
(ii) ST is a horizontal line because, it is drawn parallel to the XY-plane.
(iii) So we get: ∠PSR = ∠QTR = 90^o
(iv) Angle at R is common to both triangles.
(v) So we have two angles same in both triangles. Consequently, the third angles (∠SPR and ∠TQR) will also be the same.
5. Since angles are the same in the two triangles, they are similar triangles.
• Since they are similar triangles, we can take ratio of sides:

(i) $\frac{\text{Side opposite ∠R in ΔPRS}}{\text{Side opposite ∠R in ΔQRT}}~=~\frac{\text{SP}}{\text{TQ}}$

(ii) $\frac{\text{Side opposite ∠PSR in ΔPRS}}{\text{Side opposite ∠QTR in ΔQRT}}~=~\frac{\text{PR}}{\text{QR}}~=~\frac{m}{n}$

(iii) $\frac{\text{Side opposite ∠SPR in ΔPRS}}{\text{Side opposite ∠TQR in ΔQRT}}~=~\frac{\text{SR}}{\text{TR}}$

6. For similar triangles, the three ratios will be equal. So we get:

$\frac{\text{SP}}{\text{TQ}}~=~\frac{m}{n}~=~\frac{\text{SR}}{\text{TR}}$ 

• We need only the first two ratios. We can write:

$\frac{m}{n}~=~\frac{\text{SP}}{\text{TQ}}$

7. Now we can write the lengths in terms of 'z'. It can be done in two steps:
(i) From fig.12.14, we get:
SP = SL – PL
• S is at the same level as R.
So SL = RN = z
• Also, PL = height of P = z₁
• Therefore, SP = z-z₁
(ii) Again from Fig.12.14, we get:
TQ = QM – TM
• T is at the same level as R
So TM = RN = z
• Also, QM = height of Q = z₂
• Therefore, TQ = z₂ – z
8. Substituting for SP and TQ in (6), we get:

$\begin{array}{ll}
{}&{\frac{m}{n}}
& {~=~}& {\frac{z - z_1}{z_2 - z}}
&{} \\

{\Rightarrow}&{m(z_2 - z)}
& {~=~}& {n(z - z_1)}
&{} \\

{\Rightarrow}&{m z_2 ~-~m z}
& {~=~}& {n z ~-~n z_1}
&{} \\

{\Rightarrow}&{m z_2 ~+~n z_1}
& {~=~}& {n z ~+~ m z}
&{} \\

{\Rightarrow}&{(m~+~n)z}
& {~=~}& {m z_2 ~+~n z_1}
&{} \\

{\Rightarrow}&{z}
& {~=~}& {\frac{m z_2 + n z_1}{m+n}}
&{} \\

\end{array}$

---

• So we obtained the z-coordinate of R. We did this by dropping perpendiculars from P and Q, onto the XY-plane.
• If we drop perpendiculars from P and Q, onto the XZ-plane, we will get the y-coordinate of R.
• If we drop perpendiculars from P and Q, onto the YZ-plane, we will get the x-coordinate of R.
• The perpendiculars onto the XZ-plane is shown in fig.12.16 below:

Fig.12.16

• In the above fig.12.16, we see the two similar triangles ΔPRS and ΔQRT.
• Based on the above fig., the reader may write all the steps for the y-coordinate in his/her own notebooks.
   ♦ The result will be: $y~=~\frac{m y_2 + n y_1}{m+n}$
• Similarly, the reader may draw the diagrams and write the steps for x-coordinate also.
   ♦ The result will be: $x~=~\frac{m x_2 + n x_1}{m+n}$

---

So we can write a summary:

Case 1:
   ♦ P(x₁,y₁,z₁) and Q(x₂,y₂,z₂) are two points in space.
   ♦ Point R divides the line segment PQ internally in the ratio m:n
   ♦ Then the coordinates of R will be: $\left(\frac{m x_2 + n x_1}{m+n},~\frac{m y_2 + n y_1}{m+n},~\frac{m z_2 + n z_1}{m+n} \right)$

Case 2:
   ♦ P(x₁,y₁,z₁) and Q(x₂,y₂,z₂) are two points in space.
   ♦ Point R divides the line segment PQ externally in the ratio m:n
   ♦ Then the coordinates of R will be: $\left(\frac{m x_2 - n x_1}{m-n},~\frac{m y_2 - n y_1}{m-n},~\frac{m z_2 - n z_1}{m-n} \right)$

Case 3:
   ♦ Consider case 1.
   ♦ If R is the midpoint of PQ, then m:n will be 1:1
   ♦ So the coordinates of R will be: $\left(\frac{1 × x_2 + 1 × x_1}{1+1},~\frac{1 × y_2 + 1 × y_1}{1+1},~\frac{1 × z_2 + 1 × z_1}{1+1} \right)$
   ♦ That means: If R is the midpoint, then it's coordinates will be: $\left(\frac{x_2 + x_1}{2},~\frac{y_2 + y_1}{2},~\frac{z_2 + z_1}{2} \right)$

Case 4:
   ♦ Any ratio m:n can be written as k:1
   ♦ For that, we divide both m and n by n
   ♦ $\frac{m}{n}~=~\frac{m/n}{n/n}~=~\frac{m/n}{1}~=~\frac{k}{1}$
         ✰ So we get: $k~=~\frac{m}{n}$
   ♦ So the coordinates of R will be: $\left(\frac{k × x_2 + 1 × x_1}{k+1},~\frac{k × y_2 + 1 × y_1}{k+1},~\frac{k × z_2 + 1 × z_1}{k+1} \right)$
   ♦ That means, coordinates of R are: $\left(\frac{k x_2 + x_1}{1+k},~\frac{k y_2 + y_1}{1+k},~\frac{k z_2 + z_1}{1+k} \right)$
• This case 4 is helpful in some special problems where, we need to calculate only one unknown value 'k' instead of two unknown values 'm' and 'n'.

---

Now we will see a solved example:

Solved example 12.7
Find the coordinates of point R which divides the line segment joining P(1,-2,3) and Q(3,4,-5) in the ratio 2:3 (i) internally, (ii) externally.
Solution:
Part (i): Dividing internally
1. The ratio m:n is 2:3
2. Coordinates of R will be: $\left(\frac{m x_2 + n x_1}{m+n},~\frac{m y_2 + n y_1}{m+n},~\frac{m z_2 + n z_1}{m+n} \right)$
3. Substituting the values, we get:
$\left(\frac{2 × 3 + 3 × 1}{2+3},~\frac{2 × 4 + 3 × -2}{2+3},~\frac{2 × -5 + 3 × 3}{2+3} \right)$
⇒ $\left(\frac{6 + 3}{5},~\frac{8 -6}{5},~\frac{-10 + 9}{5} \right)$
⇒ $\left(\frac{9}{5},~\frac{2}{5},~\frac{-1}{5} \right)$

Part (ii): Dividing externally
1. The ratio m:n is 2:3
2. Coordinates of R' will be: $\left(\frac{m x_2 - n x_1}{m-n},~\frac{m y_2 - n y_1}{m-n},~\frac{m z_2 - n z_1}{m-n} \right)$
3. Substituting the values, we get:
$\left(\frac{2 × 3 - 3 × 1}{2-3},~\frac{2 × 4 - 3 × -2}{2-3},~\frac{2 × -5 - 3 × 3}{2-3} \right)$
⇒ $\left(\frac{6 - 3}{-1},~\frac{8 +6}{-1},~\frac{-10 - 9}{-1} \right)$
⇒ $\left(\frac{3}{-1},~\frac{14}{-1},~\frac{-19}{-1} \right)$
⇒ (-3, -14, 19)

Check:
1. Fig.12.17 below shows the actual plot:

Fig.12.17

2. We have the coordinates of all four points:
P(1,-2,3), Q(3,4,-5), R(9/5, 2/5, -1/5) and R'(-3, -14, 19)
3. First we will check the internal division:
• Using the distance formula, we can find the lengths:
    ♦ PR = 37/9 units
    ♦ QR = 49/8 units
• Thus the ratio PR/QR = $\frac{37/9}{49/8}~=~\frac{2}{3}$
4. Next we will check the external division:
• Using the distance formula, we can find the lengths:
    ♦ PR' = 102/5 units
    ♦ QR' = 153/5 units
• Thus the ratio PR'/QR' = $\frac{102/5}{153/5}~=~\frac{2}{3}$ 

---

In the next section, we will see a few more solved examples. 

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 12.3 - Distance Between Two Points

In the previous section, we completed a discussion on the basics of the rectangular coordinate system. In this section, we will see distance between two points.

• Consider a two-dimensional problem in which two points P(x₁,y₁) and Q(x₂,y₂) lie on the XY-plane.
   ♦ We know that, the distance PQ will be $\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2}$.
• Now we will derive a formula to find the distance between two points P(x₁,y₁,z₁) and Q(x₂,y₂,z₂) which lie in space.
• It can be derived in 10 steps:
1. In fig.12.11(a) below, P(x₁,y₁,z₁) and Q(x₂,y₂,z₂) are two points in space.
• To derive the formula, we need a rectangular prism in which PQ is a diagonal.

Fig.12.11

2. The rectangular prism can be obtained in 5 steps:
(i) Draw two magenta planes.
   ♦ Those two planes must be parallel to the XY-plane.
         ✰ One plane must pass through P.
         ✰ The other plane must pass through Q.
(ii) Draw two yellow planes.
   ♦ Those two planes must be parallel to the XZ-plane.
         ✰ One plane must pass through P.
         ✰ The other plane must pass through Q.
(iii) Draw two gray planes.
   ♦ Those two planes must be parallel to the YZ-plane.
         ✰ One plane must pass through P.
         ✰ The other plane must pass through Q.
(iv) We have drawn six planes.
• The six planes together enclose a three-dimensional-shape.
   ♦ The planes were drawn parallel to the coordinate planes.
   ♦ So all interior angles of the three-dimensional-shape are 90^o
   ♦ So the three-dimensional-shape is a rectangular prism.
• Also note that, PQ is a diagonal of this rectangular prism.
3. We want four points from the rectangular prism.
   ♦ They are: P, Q, A and N
• Remember that, our task is to find the distance PQ.
4. Let us obtain a right angled triangle inside the prism. It can be obtained in 5 steps:
(i) Consider the magenta plane in which PA lies.
(ii) Also consider the yellow plane in which AQ lies.
(iii) The magenta plane is perpendicular to the yellow plane.
   ♦ So PA is perpendicular to AQ.
(iv) Thus the angle between PA and AQ is 90^o. This is shown in fig.b
(v) We can write:
PAQ is a right angled triangle. It is right angled at A
• So we get: PQ² = PA² + AQ²
5. Let us obtain one more right angled triangle inside the prism. It can be obtained in 5 steps:
(i) Consider the magenta plane in which AN lies.
(ii) Also consider the yellow plane in which NQ lies.
(iii) The magenta plane is perpendicular to the yellow plane.
   ♦ So AN is perpendicular to NQ
(iv) Thus the angle between AN and NQ is 90^o. This is shown in fig.b
(v) We can write:
ANQ is a right angled triangle. It is right angled at N.
• So we get: AQ² = AN² + NQ²
6. Now we can substitute for AQ in (4). We get:
PQ² = PA² + AN² + NQ²
• So to find PQ, we need PA, AN and NQ
7. First we will find PA. It can be done in 4 steps:
(i) Consider the line PA
   ♦ PA lies on the yellow plane, which is parallel to the YZ-plane.
   ♦ All points on that yellow plane will have the same x-coordinate.
   ♦ So P and A will have the same x-coordinate.
(ii) PA lies on the magenta plane, which is parallel to the XY-plane.
   ♦ All points on that magenta plane will have the same z-coordinate.
   ♦ So P and A will have the same z-coordinate.
(iii) We need to pay special attention to the y-coordinates of P and A. They will be different.
   ♦ We already know the y-coordinate of P. It is: y₁
• Point A lies on the yellow plane passing through Q.
   ♦ So the y-coordinates of A and Q will be the same, which is y₂
(iv) So the distance PA = y₂ – y₁
8. Using a similar analysis as in (7), we will get:
   ♦ AN = x₂ – x₁
   ♦ NQ = z₂ - z₁
9. Now we have the lengths PA, AN and NQ
• Substituting those lengths in (6), we get:
PQ² = (y₂ – y₁)² + (x₂ – x₁)² + (z₂ – z₁)²
• So the distance formula is: $\rm{PQ}~=~\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}$
10. Suppose that, point P is the origin O
• Then we can write: x₁ = 0, y₁ = 0 and z₁ = 0
• So the distance formula becomes:
$\rm{OQ}~=~\sqrt{x_2^2~+~y_2^2~+~z_2^2}$
   ♦ This formula gives the distance of any point Q from the origin.

---

Now we will see some solved examples.

Solved example 12.3
Find the distance between the points P(1, –3, 4) and Q (– 4, 1, 2).
Solution:
1. We have the distance formula:
$\rm{PQ}~=~\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}$
2. So we get:

$\begin{array}{ll}
{}&{\rm{PQ}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(-4 - 1)^2~+~(1 -~-3)^2~+~(2 - 4)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(-5)^2~+~(4)^2~+~(-2)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{25~+~16~+~4}}
&{} \\

{}&{}
& {~=~}& {\sqrt{45}}
&{} \\

{}&{}
& {~=~}& {3\sqrt{5}~\rm{units}}
&{} \\

\end{array}$

Solved example 12.4
Show that the points P (–2, 3, 5), Q (1, 2, 3) and R (7, 0, –1) are collinear.
Solution:
1. We are given three points P, Q and R
• Using those three points, we can draw three line segments:
PQ, QR and PR
• Let us find the lengths of those three line segments.
2. First we will find PQ

$\begin{array}{ll}
{}&{\rm{PQ}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(1 -~-2)^2~+~(2 - 3)^2~+~(3 - 5)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(3)^2~+~(-1)^2~+~(-2)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{9~+~1~+~4}}
&{} \\

{}&{}
& {~=~}& {\sqrt{14}~\rm{units}}
&{} \\

\end{array}$

3. Next, we will find QR

$\begin{array}{ll}
{}&{\rm{QR}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(7 - 1)^2~+~(0 - 2)^2~+~(-1 - 3)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(6)^2~+~(-2)^2~+~(-4)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{36~+~4~+~16}}
&{} \\

{}&{}
& {~=~}& {\sqrt{56}}
&{} \\

{}&{}
& {~=~}& {2\sqrt{14}~\rm{units}}
&{} \\

\end{array}$

4. Finally, we will find PR

$\begin{array}{ll}
{}&{\rm{PR}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(7 - ~-2)^2~+~(0 - 3)^2~+~(-1 - 5)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(9)^2~+~(-3)^2~+~(-6)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{81~+~9~+~36}}
&{} \\

{}&{}
& {~=~}& {\sqrt{136}}
&{} \\

{}&{}
& {~=~}& {3\sqrt{14}~\rm{units}}
&{} \\

\end{array}$

5. We see that: PQ + QR = (√14 + 2√14) = 3√14 = PR
• In the fig.12.12 below, PR is the shortest distance from P to R.

Fig.12.12

• If we move from P to R through Q, then the distance will be greater.
• It follows that:
If Q is not in line with P and R. the sum (PQ + QR) will be greater than PR.
• But we saw that, the sum is equal to PR.
• So we can write: P, Q and R are collinear.
6. In the above fig.12.12, it is clear that, (PQ' + Q'R) cannot be less than PR.
• That means, there are only two possibilities:
   ♦ The sum is equal to PR.
   ♦ The sum is greater than PR.
7. Based on the above step (6), we can write the general steps to check whether three points are collinear:
(i) We are given three points P, Q and R.
(ii) Find the lengths PQ, QR and PR.
(iii) Pick out the longest length.
(iv) Add the remaining two lengths.
(v) If the sum is equal to the longest length, then the three points are collinear.
(vi) If the sum is greater than the longest length, then the three points are not collinear. 

Solved example 12.5
Are the points A (3, 6, 9), B (10, 20, 30) and C (25, – 41, 5), the vertices
of a right angled triangle?
Solution:
1. We are given three points A, B and C
• Using those three points, we can draw three line segments:
AB, BC and AC
• Let us find the lengths of those three line segments.
2. First we will find AB

$\begin{array}{ll}
{}&{\rm{AB}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(10 -3)^2~+~(20 - 6)^2~+~(30 - 9)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(7)^2~+~(14)^2~+~(21)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{49~+~196~+~441}}
&{} \\

{}&{}
& {~=~}& {\sqrt{686}~\rm{units}}
&{} \\

\end{array}$

3. Next, we will find BC

$\begin{array}{ll}
{}&{\rm{BC}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(25 - 10)^2~+~(-41 - 20)^2~+~(5 - 30)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(15)^2~+~(-61)^2~+~(-25)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{225~+~3721~+~625}}
&{} \\

{}&{}
& {~=~}& {\sqrt{4571}}
&{} \\

\end{array}$

4. Finally, we will find AC

$\begin{array}{ll}
{}&{\rm{AC}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(25 - ~3)^2~+~(-41 - 6)^2~+~(5 - 9)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(22)^2~+~(-47)^2~+~(-4)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{484~+~2209~+~16}}
&{} \\

{}&{}
& {~=~}& {\sqrt{2709}}
&{} \\

\end{array}$

5. Based on the above steps, we get:
AB² = 686, BC² = 4571 and AC² =2709

6.Now we can check whether A, B and C are the vertices of a right angled triangle.
(i) In the above result, mark out the largest square, which is BC²
(ii) Add the remaining squares:
AB² + AC² = (686 + 2709) = 3395
(iii) We see that, AB² + AC²≠ BC²
• So the vertices do not form a right angled triangle.

Solved example 12.6
Find the equation of the set of points P such that PA² + PB² = 2k², where A and B are points (3,4,5) and (-1,3,-7) respectively.
Solution:
1. Let the coordinates of P be (x,y,z)
2. Then PA² = (x-3)² + (y-4)² + (z-5)^2
3. Also, PB² = (x+1)² + (y-3)² + (z+7)^2
4. So we can write:
PA² + PB² = (x-3)² + (y-4)² + (z-5)^2 + (x+1)² + (y-3)² + (z+7)^2
= x² - 6x + 9 + y² -8y + 16 + z² - 10z + 25
+ x² +2x + 2 + y² -6y + 9 + z² + 14z + 49

= 2x² -4x + 11 +2y² -14y +25 +z² +4z +64
= 2x² + 2y² + 2z² -4x -14y +4z +100
5. So the given equation becomes:
2x² + 2y² + 2z² - 4x - 14y + 4z + 100 = 2k²
⇒ x² + y² + z² - 2x - 7y + 2z + 50 = k²

---

The link below gives a few more solved examples:

Exercise 12.2

---

In the next section, we will see section formula. 

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 12.2 - Another Method to Find Coordinates of A Point In Space

In the previous section, we accomplished two tasks:

Task 1:
To find the coordinates of a point with reference to x, y and z-axes.
Task 2: To mark a point in space when the coordinates of that point are given.
(Task 2 is the converse of task 1)
• The same two tasks can be accomplished using another method. In this section, we will see this new method.

◼ First we will see task 1:
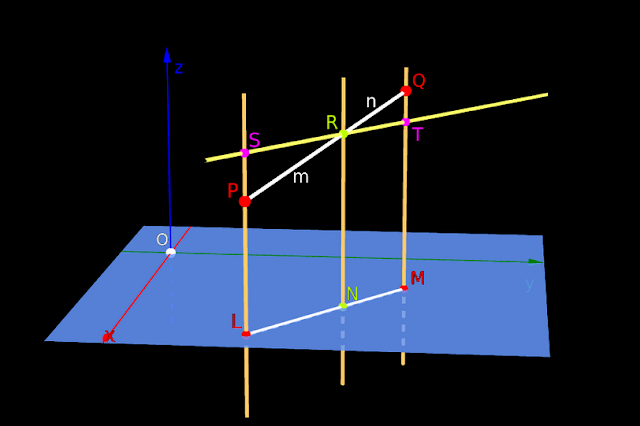
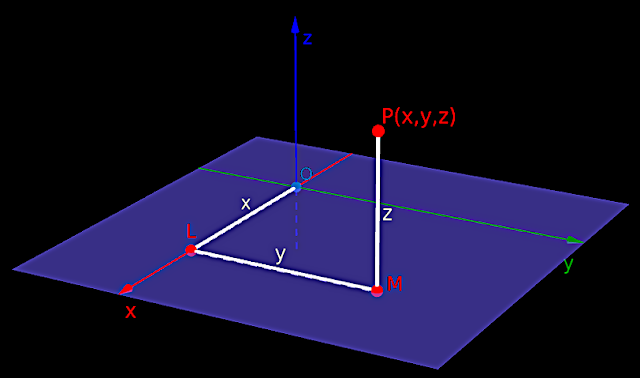
• In fig.12.7 below, P is a point in space.

Fig.12.7

• We want to write the position of P. It can be done in 4 steps:
1. The first step always is to draw a plane.
• This plane should be:
    ♦ Passing through P.
    ♦ Parallel to the YZ-plane.
• In the fig.12.7 above, this plane is shown in gray color.
• Mark the point A where this plane intersects the x-axis.
    ♦ Measure the length OA.
• This length is indicated as ‘x’.
    ♦ If A is on the +ve side of the x-axis, then x is +ve.  
    ♦ If A is on the -ve side of the x-axis, then x is -ve.
2. The second step always is to draw a second plane.
• This plane should be:
    ♦ Passing through P.
    ♦ Parallel to the XZ-plane.
• In the fig.12.7 above, this plane is shown in yellow color.
• Mark the point B where this plane intersects the y-axis.
    ♦ Measure the length OB.
• This length is indicated as ‘y’.
    ♦ If B is on the +ve side of the y-axis, then y is +ve.  
    ♦ If B is on the -ve side of the y-axis, then y is -ve.
3. The third step always is to draw a third plane.
• This plane should be:
    ♦ Passing through P.
    ♦ Parallel to the XY-plane.
• In the fig.12.7 above, this plane is shown in magenta color.
• Mark the point C where this plane intersects the z-axis.
    ♦ Measure the length OC.
• This length is indicated as ‘z’.
    ♦ If C is above the XY-plane, then z is +ve.  
    ♦ If C is below the XY-plane, then z is -ve.
4. The fourth and final step always is to write x, y and z together as an ordered triplet: (x,y,z)
• To specify the position of point P, we write: P(x,y,z)

---

Let us see two examples.
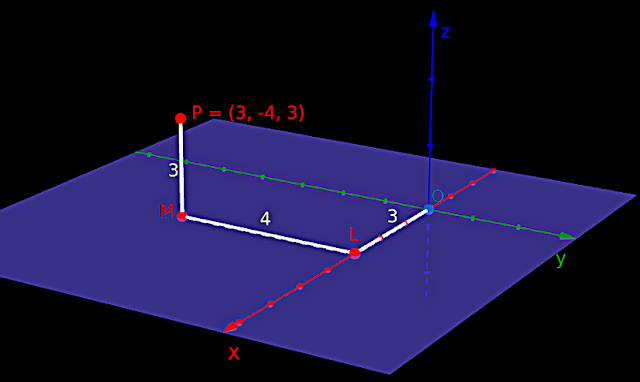
Example 1:
This can be written in 5 steps:
1. In fig.12.8 below, P is a point in space. Let us assume that, it's position is not known. Our task is to find it's position with reference to the three axes.

Fig.12.8

2. First we draw a plane.
• This plane is:
    ♦ Passing through P.
    ♦ Parallel to the YZ-plane.
• In the fig.12.8 above, this plane is shown in white color.
    ♦ This plane intersects the x-axis at A
    ♦ Length OA is 3 units.
    ♦ A is on the +ve side of the x-axis. So x = 3
3. Next we draw another plane.
• This plane is:
    ♦ Passing through P.
    ♦ Parallel to the XZ-plane.
• In the fig.12.8 above, this plane is shown in yellow color.
    ♦ This plane intersects the y-axis at B.
    ♦ Length OB is 4 units.
    ♦ B is on the -ve side of the y-axis. So y = -4
4. Next we draw a third plane.
• This plane is:
    ♦ Passing through P.
    ♦ Parallel to the XY-plane.
• In the fig.12.8 above, this plane is shown in magenta color.
    ♦ This plane intersects the z-axis at C.
    ♦ Length OC is 3 units.
    ♦ C is on the +ve side of the z-axis. So z = 3
5. So we can write the coordinates of P as: P(3,-4,3)

Example 2:
This can be written in 5 steps:
1. In fig.12.9 below, P is a point in space. Let us assume that, it's position is not known. Our task is to find it's position with reference to the three axes.

Fig.12.9

2. First we draw a plane.
• This plane is:
    ♦ Passing through P.
    ♦ Parallel to the YZ-plane.
• In the fig.12.9 above, this plane is shown in gray color.
    ♦ This plane intersects the x-axis at A
    ♦ Length OA is 4 units.
    ♦ A is on the -ve side of the x-axis. So x = -4
3. Next we draw another plane.
• This plane is:
    ♦ Passing through P.
    ♦ Parallel to the XZ-plane.
• In the fig.12.9 above, this plane is shown in yellow color.
    ♦ This plane intersects the y-axis at B.
    ♦ Length OB is 3 units.
    ♦ B is on the +ve side of the y-axis. So y = 3
4. Next we draw a third plane.
• This plane is:
    ♦ Passing through P.
    ♦ Parallel to the XY-plane.
• In the fig.12.9 above, this plane is shown in magenta color.
    ♦ This plane intersects the z-axis at C.
    ♦ Length OC is 5 units.
    ♦ C is on the -ve side of the z-axis. So z = -5
5. So we can write the coordinates of P as: P(-4,3,-5)

---

◼ Now we will see how task 2 is accomplished using this method.
• Consider fig.12.7 that we saw at the beginning of this section. For convenience, it is shown again below:

Fig.12.7

• We are given the coordinates (x,y,z) of point P. We want to mark that point P in space. It can be done in 4 steps:
1. The first step always is to start from O and move along the x-axis.
   ♦ If the given ‘x’ is +ve, we must move in the +ve x direction.
   ♦ If the given ‘x’ is -ve, we must move in the -ve x direction.
• Mark a point A in such a way that, OA = x units.
• Now draw a plane. This plane should be:
    ♦ Passing through A.
    ♦ Parallel to the YZ-plane.
• In the fig.12.7 above, this plane is shown in gray color.
2. The second step always is to start from O and move along the y-axis.
   ♦ If the given ‘y’ is +ve, we must move in the +ve y direction.
   ♦ If the given ‘y’ is -ve, we must move in the -ve y direction.
• Mark a point B in such a way that, OB = x units.
• Now draw a plane. This plane should be:
    ♦ Passing through B.
    ♦ Parallel to the XZ-plane.
• In the fig.12.7 above, this plane is shown in yellow color.
3. The third step always is to start from O and move along the z-axis.
   ♦ If the given ‘z’ is +ve, we must move in the +ve z direction.
   ♦ If the given ‘z’ is -ve, we must move in the -ve z direction.
• Mark a point C in such a way that, OA = x units.
• Now draw a plane. This plane should be:
    ♦ Passing through C.
    ♦ Parallel to the XY-plane.
• In the fig.12.7 above, this plane is shown in magenta color.
4. The point of intersection of the three planes is the position of P.

---

Let us see two examples.
Example 1:
This can be written in 5 steps:
1. Consider the fig.12.8 that we saw earlier. For convenience, it is shown again below:

Fig.12.8

2. First we start from O and move along the x-axis.
• Since the given x is +ve, we move along the +ve direction of x-axis.
• We mark the point A in such a way that, length of OA is 3 units.
• Now draw a plane. This plane should be:
    ♦ Passing through A.
    ♦ Parallel to the YZ-plane.
• In the fig.12.8 above, this plane is shown in white color.
3. Next we start from O and move along the y-axis.
• Since the given y is -ve, we move along the -ve direction of y-axis.
• We mark the point B in such a way that, length of OB is 4 units.
• Now draw a plane. This plane should be:
    ♦ Passing through B.
    ♦ Parallel to the XZ-plane.
• In the fig.12.8 above, this plane is shown in yellow color.
4. Next we start from O and move along the z-axis.
• Since the given z is +ve, we move along the +ve direction of z-axis.
• We mark the point C in such a way that, length of OC is 3 units.
• Now draw a plane. This plane should be:
    ♦ Passing through C.
    ♦ Parallel to the XY-plane.
• In the fig.12.8 above, this plane is shown in magenta color.
5. The point of intersection of the three planes is the position of P.       

Example 2:
This can be written in 4 steps:
1. Consider the fig.12.9 that we saw earlier. For convenience, it is shown again below:

Fig.12.9

2. First we start from O and move along the x-axis.
• Since the given x is -ve, we move along the -ve direction of x-axis.
• We mark the point A in such a way that, length of OA is 4 units.
• Now draw a plane. This plane should be:
    ♦ Passing through A.
    ♦ Parallel to the YZ-plane.
• In the fig.12.9 above, this plane is shown in gray color.
3. Next we start from O and move along the y-axis.
• Since the given y is +ve, we move along the +ve direction of y-axis.
• We mark the point B in such a way that, length of OB is 3 units.
• Now draw a plane. This plane should be:
    ♦ Passing through B.
    ♦ Parallel to the XZ-plane.
• In the fig.12.9 above, this plane is shown in yellow color.
4. Next we start from O and move along the z-axis.
• Since the given z is -ve, we move along the -ve direction of z-axis.
• We mark the point C in such a way that, length of OC is 5 units.
• Now draw a plane. This plane should be:
    ♦ Passing through C.
    ♦ Parallel to the XY-plane.
• In the fig.12.9 above, this plane is shown in magenta color.
5. The point of intersection of the three planes is the position of P.

---

From the above discussion, we can write three important points:
1. Consider any point P(x,y,z) in space.
    ♦ x will be the distance of P from the YZ-plane.
    ♦ y will be the distance of P from the XZ-plane.
    ♦ z will be the distance of P from the XY-plane.
2. If P is situated on any one of the three axes, then two of it’s coordinates will be zeroes.
    ♦ If P is on the x-axis, then it’s coordinates will be in the form P(x,0,0).
    ♦ If P is on the y-axis, then it’s coordinates will be in the form P(0,y,0).
    ♦ If P is on the z-axis, then it’s coordinates will be in the form P(0,0,z). 
3. If P is situated on any one of the three planes, then one of it’s coordinates will be zero.
    ♦ If P is on the XY-plane, then it’s coordinates will be in the form P(x,y,0).
    ♦ If P is on the XZ-plane, then it’s coordinates will be in the form P(x,0,z).
    ♦ If P is on the YZ-plane, then it’s coordinates will be in the form P(0,0,z).

---

• Using the signs of the three coordinates of a point P, we can easily write the octant in which P is situated. We mentioned this in the previous section.
• The converse is also possible. That is., if we are given any of the eight octants, we can easily write the signs of the coordinates of points in that octant.
• Let us see two examples:
Example 1:
What are the signs of the coordinates of points in octant II?
Solution:
1. Octant II is one of the first four octants.
    ♦ So we directly consider quadrant II.
    ♦ Name of quadrant II is X’OY
2. Since octant II is one of the first four octants, we can put Z.
    ♦ So the name of the octant II is X`OYZ
3. Based on this name, the signs are: -ve, +ve, +ve

Example 2:
What are the signs of the coordinates of points in octant VII?
Solution:
1. Octant VII is one of the last four octants.
• The octant occurring above octant VII is: (7-4) = octant III
    ♦ So we consider quadrant III.
    ♦ Name of quadrant III is X’OY’
2. Since octant VII is one of the last four octants, we can put Z’.
    ♦ So the name of the octant VII is X`OY’Z’
3. Based on this name, the signs are: -ve, -ve, -ve

---

Now we will see some solved examples. 

Solved example 12.1
In fig.12.10 below, the coordinates of P are (2,4,5). What are the coordinates of the point F ?

Fig.12.10

Solution:
1. The gray plane is parallel to the YZ-plane. So all points on the gray plane will have the same x-coordinate.
• P(2,4,5) lies on the gray plane. So all points on the gray plane will have the x-coordinate ‘2’
• The point F lies on the gray plane. So the x-coordinate of F is ‘2’.
2. The magenta plane is parallel to the XY-plane. So all points on the magenta plane will have the same z-coordinate.
• P(2,4,5) lies on the magenta plane. So all points on the magenta plane will have the z-coordinate ‘5’.
• The point F lies on the magenta plane. So the z-coordinate of F is ‘5’  
3. The point F lies on the XZ-plane.
• All points on the XZ-plane will have the y-coordinate as zero.
4. Based on the above three steps, we get the coordinates of F as: (2,0,5)

Solved example 12.2
Find the octants in which the points (-3,1,2) and (-3,1,-2) lie.
Solution:
Case 1: (-3,1,2)
1. The signs are: -ve, +ve, +ve
    ♦ Based on the first two signs, we can write: X’OY
    ♦ Based on the last sign, we get: Z
• So the name of the octant is X’OYZ
• Since Z is +ve, it is one of the first four octants.
2. The first three letters of the name are: X’OY.
• This corresponds to the quadrant II
3. Since it is one of the first four octants, the names of quadrants and octants are same.
• We get: octant II
Case 2: (-3,1,-2)
1. The signs are: -ve, +ve, -ve
    ♦ Based on the first two signs, we can write: X’OY
    ♦ Based on the last sign, we get: Z’
• So the name of the octant is X’OYZ’
• Since Z is -ve, it is one of the last four octants.
2. The first three letters of the name are: X’OY.
• This corresponds to the quadrant II
3. Since it is one of the last four octants, we must add 4.
    ♦ 2+4 = 6
• We get: octant VI

---

The link below gives a few more solved examples:

Exercise 12.1

---

In the next section, we will see distance between two points. 

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 12.1 - Coordinates of a Point in Space

In the previous section, we saw the basics of the rectangular coordinate system. In this section, we will see how this system can be used to fix the position of any object in space.

• In fig.12.4 below, P is a point in space.

Fig.12.4

• We want to write the position of P. It can be done in 6 steps:
1. The first step always is to drop a perpendicular from the given point, onto the XY-plane.
• In the above fig.12.4, the foot of the perpendicular is marked as M.
    ♦ We must measure the length of PM.
• PM is parallel to the z-axis. So the length of PM is denoted as ‘z’.
• ‘z’ should be given the proper sign.
    ♦ If PM is above the XY-plane, then z is +ve.
    ♦ If PM is below the XY-plane, then z is -ve.
2. The second step always is to drop a perpendicular from M onto the x-axis.
• In the above fig.12.4, the foot of the perpendicular is marked as L.
    ♦ We must measure the length of ML.
• ML is parallel to the y-axis. So the length of ML is denoted as ‘y’.
• ‘y’ should be given the proper sign.
    ♦ If ML is on the +ve side of the y-axis, then y is +ve.
    ♦ If ML is on the -ve side of the y-axis, then y is -ve.
3. The third step always is to measure OL.
• OL is on the x-axis. So the length of OL is denoted as ‘x’.
• ‘x’ should be given the proper sign.
    ♦ If OL is on the +ve side of the x-axis, then x is +ve.
    ♦ If OL is on the -ve side of the x-axis, then x is -ve.
4. The fourth and final step always is to write x, y and z together as an ordered triplet: (x,y,z)
• To specify the position of point P, we write: P(x,y,z)
5. Since x, y and z are given the proper signs, anybody can get an idea about the octant in which P is situated.
6. Anybody can get an idea about the distances also.
    ♦ The magnitude of x is the distance of P from the YZ-Plane.
    ♦ The magnitude of y is the distance of P from the XZ-Plane.
    ♦ The magnitude of z is the distance of P from the XY-Plane.

---

Let us see two examples.
Example 1:
This can be written in 6 steps:
1. In fig.12.5 below, P is a point in space. Let us assume that, it's position is not known. Our task is to find it's position with reference to the three axes.

Fig.12.5

2. First we drop the perpendicular PM onto the XY-plane. Then we measure the length of PM. In our present case, the length is 3 units.
• PM is parallel to the z-axis.
• PM is above the XY-plane.
   ♦ So z is +ve. We can write: z = 3
3. Next we drop the perpendicular ML onto the x-axis. Then we measure the length of ML. In our present case, the length is 4 units.
• ML is parallel to the y-axis.
• ML is on the -ve side of the y-axis.
   ♦ So y is -ve. We can write: y = -4
4. Finally, we measure the length of OL. In our present case, the length is 3 units.
• OL lies on the x-axis.
• OL is on the +ve side of the x-axis.
   ♦ So x is +ve. We can write: x = 3
5. So we obtained the values of x, y and z.
• We write it as an ordered triplet: (3, -4, 3)
• Thus the coordinates of P are written as: P(3, -4,3)      
6. Using the sign of each coordinate, we can write the name of the octant. It can be done in 5 steps:
(i) z is +ve. So we get Z. It is one of the first four octants.
(ii)  x is +ve and y is -ve. So we get XOY’
(iii) Thus the name of the octant is XOY’Z
(iv) The first three letters are XOY’.
• Comparing this with the name of the quadrants of two-dimensional problems, we see that, XOY’ is the name of the fourth quadrant.
(v) So we can write:
The given point P is in the octant IV.

Example 2:
This can be written in 6 steps:
1. In fig.12.6 below, P is a point in space. Let us assume that, it's position is not known. Our task is to find it's position with reference to the three axes.

Fig.12.6

2. First we drop the perpendicular PM onto the XY-plane. Then we measure the length of PM. In our present case, the length is 5 units.
• PM is parallel to the z-axis.
• PM is below the XY-plane.
   ♦ So z is -ve. We can write: z = -5
3. Next we drop the perpendicular ML onto the x-axis. Then we measure the length of ML. In our present case, the length is 3 units.
• ML is parallel to the y-axis.
• ML is on the +ve side of the y-axis.
   ♦ So y is +ve. We can write: y = 3
4. Finally, we measure the length of OL. In our present case, the length is 4 units.
• OL lies on the x-axis.
• OL is on the -ve side of the x-axis.
   ♦ So x is -ve. We can write: x = -4
5. So we obtained the values of x, y and z.
• We write it as an ordered triplet: (-4, 3, -5)
• Thus the coordinates of P are written as: P(-4, 3, -5)      
6. Using the sign of each coordinate, we can write the name of the octant. It can be done in 5 steps:
(i) z is -ve. So we get Z'. It is one of the last four octants.
(ii)  x is -ve and y is +ve. So we get X’OY
(iii) Thus the name of the octant is X’OYZ'
(iv) The first three letters are X’OY.
• Comparing this with the name of the quadrants of two-dimensional problems, we see that, X’OY is the name of the second quadrant.
    ♦ The octant below second octant is (2+4) = 6
(v) So we can write:
The given point P is in the octant VI.

---

• So far in this section, we have been discussing this:
Given a point in space. How to find the coordinates of that point?
• We must be able to do the reverse also:
Given the coordinates of a point in space. How will we mark that point in space?
• This is similar to the task of the electrician that we saw in the previous section. He knows the measurements. His task is to use those measurements and hang the lamp at the correct position.

• Consider fig.12.4 that we saw at the beginning of this section. For convenience, it is shown again below:

Fig.12.4

• We are given the coordinates (x,y,z) of point P. We want to mark that point P in space. It can be done in 3 steps:
1. The first step always is to start from O and move along the x-axis.
   ♦ If the given ‘x’ is +ve, we must move in the +ve x direction.
   ♦ If the given ‘x’ is -ve, we must move in the -ve x direction.
• Mark a point L in such a way that, OL = x units.
2. The second step always is to draw a line LM perpendicular to the x-axis.
   ♦ If the given ‘y’ is +ve, we must draw LM towards +ve y direction.
   ♦ If the given ‘y’ is -ve, we must draw LM towards -ve y direction.
• The length of LM should be y units.
• Also, LM must lie on the XY-plane.
3. The third step always is to draw a line MP perpendicular to the XY-plane.
   ♦ If the given ‘z’ is +ve, we must draw MP upwards from the XY-plane.
   ♦ If the given ‘z’ is -ve, we must draw MP downwards from the XY-plane.
• The length of MP must be z units.
• The end P of the line MP is the required point.

---

Let us see two examples.
Example 1:
This can be written in 4 steps:
1. Consider the fig.12.5 that we saw earlier. For convenience, it is shown again below:

Fig.12.5

• Coordinates of P are given: (3,-4,3)
• Our task is to mark the position of P in space.   
2. First we start from O and move along the x-axis.
• Since the given x is +ve, we move along the +ve direction of x-axis.
• We mark the point L in such a way that, length of OL is 3 units.
3. Next we draw LM, perpendicular to the x-axis.
• Since the given y is -ve, we must draw LM towards the -ve y direction.
• Length of LM must be 4 units.
• Also, LM must lie on the XY-plane.
4. Finally we draw MP, perpendicular to the XY-plane.
• Since the given z is +ve, we must draw MP upwards from the XY-plane.
• Length of MP must be 3 units.
• The end P of the line MP is the required position.       

Example 2:
This can be written in 4 steps:
1. Consider the fig.12.6 that we saw earlier. For convenience, it is shown again below:

Fig.12.6

• Coordinates of P are given: (-4,3,-5)
• Our task is to mark the position of P in space.   
2. First we start from O and move along the x-axis.
• Since the given x is -ve, we move along the -ve direction of x-axis.
• We mark the point L in such a way that, length of OL is 4 units.
3. Next we draw LM, perpendicular to the x-axis.
• Since the given y is +ve, we must draw LM towards the +ve y direction.
• Length of LM must be 3 units.
• Also, LM must lie on the XY-plane.
4. Finally we draw MP, perpendicular to the XY-plane.
• Since the given z is -ve, we must draw MP downwards from the XY-plane.
• Length of MP must be 5 units.
• The end P of the line MP is the required position.

---

• In this section, we accomplished two tasks:
Task 1:
To find the coordinates of a point with reference to x, y and z-axes.
Task 2: To mark a point in space when the coordinates of that point are given.
(Task 2 is the converse of task 1)
• The same two tasks can be accomplished using another method. We will see it in the next section. 

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com