In the previous section, we saw the basics about derivatives. We saw that, derivative is the rate of change. In this section, we will see another use of derivatives.
It can be written in 9 steps:
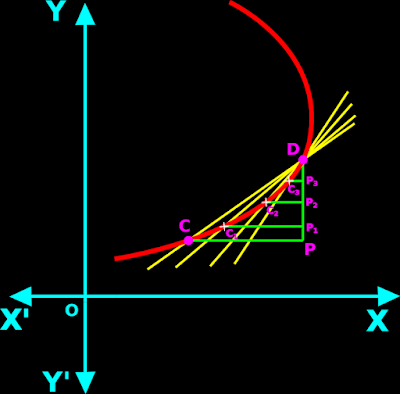
1. In fig.13.28 below, the red curve is the graph of a function f(x).
 |
| Fig.13.28 |
• C and D are two adjacent points on the graph.
• A yellow line connects C and D.
♦ A vertical green line is drawn through D.
♦ A horizontal green line is drawn through C.
• These vertical and horizontal green lines intersect at P.
• So we get a right triangle CPD
• We know that, slope of the line CD will be given by the ratio $\frac{\rm{PD}}{\rm{PC}}$
• The line CD intersects the red curve at two points C and D
2. Keeping D fixed, let us consider a point which is closer to D
• This new point is marked as C1 in the fig.13.28
♦ A horizontal green line is drawn through C1
• Thus we get a right triangle C1P1D
• So slope of the line C1D will be given by the ratio $\rm{\frac{P_1 D}{P_1 C_1}}$
• Note that:
♦ the denominator of this ratio
♦ is smaller than
♦ the denominator of the ratio in (1)
3. Keeping D fixed, let us consider a point which is still closer to D
• This new point is marked as C2 in the fig.13.28
♦ A horizontal green line is drawn through C2
• Thus we get a right triangle C2P2D
• So slope of the line C2D will be given by the ratio $\rm{\frac{P_2 D}{P_2 C_2}}$
• Note that:
♦ the denominator of this ratio
♦ is smaller than
♦ the denominator of the ratio in (2)
4. Keeping D fixed, let us consider a point which is even more closer to D
• This new point is marked as C3 in the fig.13.28
♦ A horizontal green line is drawn through C3
• Thus we get a right triangle C3P3D
• So slope of the line C3D will be given by the ratio $\rm{\frac{P_3 D}{P_3 C_3}}$
• Note that:
♦ the denominator of this ratio
♦ is smaller than
♦ the denominator of the ratio in (3)
5. Proceeding like this, we can mark points C4, C5, C6, C7 etc., which are closer and closer to D
• When the point is very close to D, the yellow line will no longer intersect the red curve at two points.
• The yellow line will intersect the red curve only at one point.
• When there is only one point, we can say that:
The yellow line touches the red curve.
• The ‘touch’ occurs at D
6. When the yellow line touches the red curve at D, we say that:
The yellow line is the tangent of the red curve at D
7. Even though there is only a "touch" at one point, we still have a triangle similar to CPD.
Only difference is that, the base of that triangle will be of infinitesimal length.
• Since there is a triangle, we can take the ratio $\rm{\frac{Altitude}{Base}}$. This ratio will give the slope.
• So we can write:
Slope of the tangent = $\frac{\text{PD corresponding to infinitesimal CP}}{\text{infinitesimal CP}}$.
(We use the word “corresponding: because:
For each length of the base CP, there will be a corresponding length for the altitude PD. Even when the base is infinitesimal, there will be a corresponding altitude)
8. But in the previous section, we saw that, the ratio with infinitesimal denominator is called the derivative.
• So we can write:
The slope of the tangent at a point is same as the derivative at that point.
9. We proved that, slope is equal to the derivative. We proved this by taking point C and moving forward towards D
• We can take point E and move backward towards D. We will get the same result. This is shown in fig.13.29 below:
 |
| Fig.13.29 |
• The reader should write all steps related to fig.13.29 and become convinced that slope is same as the derivative.
• We saw two applications of derivatives.
(i) Derivative as rate of change.
(ii) Derivative as slope of tangent.
• While discussing rate of change, we did not draw the line CD. Because, for that discussion, such a line is not required.
• But while discussing slope of tangent, we did draw that line. Because, it is that line CD which gradually becomes the tangent at D. This gradual change occurs when the point C becomes closer and closer to D.
In the next section, we will see an easy method to find the derivative.
No comments:
Post a Comment