In the previous section,
we saw second theorem. We saw some solved examples also. In this section, we will
see the third theorem. Later in this section, we will see the sandwich theorem also.
Theorem 3
This can be written in 5 steps:
1. Consider two functions f and g.
•
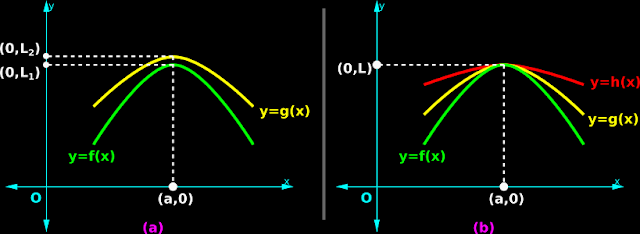
They are plotted in fig.13.20(a) below:
 |
| Fig.13.20 |
• This can be explained in 2 steps:
(i) We know that, domain of a function is a set.
• This set will contain all input x values that can be used for that function.
(ii) In our present case, both f and g should have the same domain.
• For example,
♦ the domain of f consists of all real numbers from -10 to 15,
♦ the domain of g must also be the same.
♦ -11 cannot be an input x value for g
3. In our present case, functions f and g satisfy a special condition. The condition can be written in 4 steps:
(i) Take any input x value from the domain.
(ii) Calculate f(x) corresponding to that input x.
(iii) Calculate g(x) corresponding to that input x.
(iv) f(x) should be less than g(x).
◼ Mathematically, this condition can be written as:
$f(x) < g(x)$ for all x in the domain
4. The functions in fig.13.20(a), satisfy the above condition in (3).
•
We see that:
♦ all points of the green curve, lie below the yellow curve.
5. If the condition in (3) is satisfied, then we get an useful result. It can be written in 4 steps:
(i) Take any input x (say 'a') from the domain.
(ii) Calculate $\lim_{x\rightarrow a} f(x)$ corresponding to that input x.
•
We know that,$\lim_{x\rightarrow a} f(x)$ = f(a)
♦ From the fig13.20(a), we see that: f(a) = L1
(iii) Calculate $\lim_{x\rightarrow a} g(x)$ corresponding to that input x.
•
We know that,$\lim_{x\rightarrow a} g(x)$ = g(a)
♦ From the fig13.20(a), we see that: g(a) = L2
(iv) We know that f(a) < g(a). So we get:
$\lim_{x\rightarrow a} f(x)$ will be less than $\lim_{x\rightarrow a} g(x)$
•
Indeed, in fig.13.20(a), we see that, (0,L1) lies below (0,L2)
◼ Mathematically, we can write this as:
$$\lim_{x\rightarrow a} f(x) < \lim_{x\rightarrow a} g(x)$$
• The above five steps and fig.13.20(a), completely describes theorem 3.
•
Based on theorem 3, we can write theorem 4
Theorem 4
This theorem is also known as sandwich theorem. It can be written in 7 steps:
1. In fig.13.20(b) above, we see that:
f(x) < g(x) < h(x) for every x in the domain.
2. Take any input x (say 'a') from the domain.
Suppose that:
♦ f(a) is equal to L
♦ h(a) is also equal to L
3. Given that, g(x) is greater than f(x) for every x
•
So g(a) will be greater than f(a)
♦ That means, g(a) will be greater than L
4. Given also that, g(x) is lesser than h(x) for every x
•
So g(a) will be lesser than h(a)
♦ That means, g(a) will be lesser than L
5. Let us compare the above results:
♦ In (3), we have: g(a) > L
♦ In (4), we have: g(a) < L
•
Only one condition can satisfy both the inequalities. That is., g(a) = L
6. Let us write the results in terms of limits:
•
If f(a) = L, then we can write: $\lim_{x\rightarrow a} f(x) = L$
•
If g(a) = L, then we can write: $\lim_{x\rightarrow a} g(x) = L$
•
If h(a) = L, then we can write: $\lim_{x\rightarrow a} h(x) = L$
7. Based on the above steps, we can write:
If $\lim_{x\rightarrow a} f(x) = \lim_{x\rightarrow a} h(x) = l$, then $\lim_{x\rightarrow a} g(x) = L$
• The above seven steps and fig.13.20(b), completely describes the sandwich theorem.
•
Sandwich theorem can be effectively used to find the limits of complicated functions. All we need are two simple functions such that, the complicated function is sandwiched between the two simple functions. Let us see such an application. It can be written in steps:
1. In fig.13.21(a) below, a unit circle is drawn in red color.
 |
| Fig.13.21 |
• Since it is a unit circle, distances OA = OC = 1 unit
• OC makes an angle of x radians with the X-axis.
• Direction of rotation of OC is anti-clockwise. So angle x is +ve.
• A perpendicular is drawn to the X-axis at A.
♦ This perpendicular meets the extension of OC at B.
• A perpendicular is dropped from C on to the X-axis.
♦ The foot of this perpendicular is D.
• Line AC is drawn in violet color.
2. We have to find three areas:
♦ Area of triangle OAC
♦ Area of sector OAC
♦ Area of triangle OAB
3. First we will find the area of triangle OAC. It can be done in 4 steps:
(i) We have:
Area of triangle OAC = $\rm{\frac{1}{2} × OA × CD}$
(ii) Length OA = 1
(iii) In triangle ODC, $\rm{\sin x = \frac{CD}{OC} = \frac{CD}{1} = CD}$
• So CD = sin x
(iv) So from (i), we get:
Area of triangle OAC = $\rm{\frac{1}{2} × 1 × \sin x = \frac{\sin x}{2}}$
4. Next we will find the area of sector OAC. It can be done in 5 steps:
(i) When OC rotates a complete 2π radians, we get the full area of πr2 square units.
(ii) So when OC rotates 1 radian, we get an area of:
$\rm{\frac{\pi r^2}{2 \pi} = \frac{r^2}{1} = \frac{1^2}{2} = \frac{1}{2}}$ square units.
(iii) So when OC rotates x radians, we get an area of:
$\rm{x × \frac{1}{2} = \frac{x}{2}}$ square units.
(iv) But area obtained by rotating through x radians is same as the area of the sector OAC.
(v) So we can write:
Area of sector OAC = $\rm{\frac{x}{2}}$ square units.
5. Finally we will find the area of triangle OAB. It can be done in 4 steps:
(i) We have:
Area of triangle OAB = $\rm{\frac{1}{2} × OA × AB}$
(ii) Length OA = 1
(iii) In triangle OAB, $\rm{\tan x = \frac{AB}{OA} = \frac{AB}{1} = AB}$
• So AB = tan x
(iv) So from (i), we get:
Area of triangle OAB = $\rm{\frac{1}{2} × 1 × \tan x = \frac{\tan x}{2}}$
6. Comparing the three areas in the fig.13.21(a), we can see that:
♦ Area of triangle OAC is the smallest area.
♦ Area of triangle OAB is the largest area.
• So we can write:
Area of △OAC < Area of sector OAC < Area of △OAB
7. Substituting the actual areas, we get:
$\frac{\sin x}{2} < \frac{x}{2}< \frac{\tan x}{2}$
• Multiplying throughout by 2, we get:
$\rm{\sin x < x < \tan x}$
• This can be written as:
$\rm{\sin x < x < \frac{\sin x}{\cos x}}$
• Dividing by sin x, we get:
$\rm{1 < \frac{x}{\sin x} < \frac{1}{\cos x}}$
(For our present discussion, we are considering only those x values from zero to $\frac{\pi}{2}$ radians. For those x values, sin x will be +ve. So dividing by sin x will not alter the nature of the inequalities)
8. Consider the result in (7).
• If we take the reciprocals throughout, the nature of the inequalities will change. We will get:
$\rm{1 > \frac{\sin x}{x} > \frac{\cos x}{1}}$
• This can be rearranged as:
$\rm{\frac{\cos x}{1} < \frac{\sin x}{x} < 1}$
9. Consider the result in (8).
• The right term can be written as a function: f(x) = 1
• The middle term can be written as a function: g(x) = $\rm{\frac{\sin x}{x}}$
• The left term can be written as a function: h(x) = cos x
• So we get: f(x) < g(x) < h(x)
10. We want: $\lim_{x\rightarrow 0} g(x)$
• That is., we want: $\lim_{x\rightarrow 0} \left[\frac{\sin x}{x} \right]$
• Here, direct substitution is not possible because, both numerator and denominator will become zero.
11. So we try another method. It can be written in 2 steps:
(i) In (9) we saw that, g(x) lies between f(x) and h(x)
• As x approaches zero, f(x) will approach 1
♦ That is., $\lim_{x\rightarrow 0} f(x) = 1$
♦ Recall that, $\lim_{x\rightarrow 0} 1 =1$.
• As x approaches zero, h(x) will also approach 1
♦ That is., $\lim_{x\rightarrow 0} h(x) = 1$
♦ Recall that, $\lim_{x\rightarrow 0} \cos x =1$.
(ii) We want the limit at zero.
• At that point, the limits of both f(x) and h(x) are 1
• So by sandwich theorem, the limit of g(x) will also be 1
• We can write: $\lim_{x\rightarrow 0} \frac{\sin x}{x} = 1$
12. Thus we effectively used the sandwich theorem to find the limit of a complicated function.
• Fig.13.22 below shows the plot of three functions:
♦ f(x) = cos x
♦ g(x) = $\frac{\sin x}{x}$
♦ h(x) = 1
 |
| Fig.13.22 |
• Based on the plots, we can write a few more details about the limit of g(x). It can be written in 3 steps:
1. We see that, g(x) is sandwiched between f(x) and h(x)
• As x approaches zero, both f(x) and h(x) approach 1.
• So sandwich theorem is indeed applicable.
2. We used the geometrical construction in fig.13.21(a) to find the limit of $\frac{\sin x}{x}$.
• This fig. helps us to prove the right side limit $\lim_{x\rightarrow 0^{+}} \left[\frac{\sin x}{x} \right]$
• The reason can be explained in 4 steps:
(i) The angle x in fig.13.21(a) is +ve because, it is measured in the anti-clockwise direction.
(ii) So the x values obtained from this fig. are marked on the right side of the origin O.
(iii) We can approach from the right side (starting from say $\frac{\pi}{2}$) towards zero.
(iv) As we approach zero, the angle x decreases. The line OB gets closer and closer to the x-axis.
3. To prove the left side limit, we can use fig.13.21(b)
• The procedure is the same. The reader may write all the necessary steps to find the three areas. The areas can be compared to determine the required limit.
• Some points to remember are:
(i) The angle increases from $\frac{-\pi}{2}$ to zero. The line OB' gets closer and closer to the x-axis.
(ii) The angles are -ve, So sine of those angles will be -ve. (Remember the identity: sin(-x) = -sin x)
(iii) The angles are -ve. So x values are -ve.
(iv) Since the quantities in both (ii) and (iii) are -ve, the ratio $\frac{\sin x}{x}$ will be +ve.
(v) The angles are -ve. So cosine of those angles will be +ve. (Remember the identity: cos(-x) = cos x)
• We have completed a discussion on sandwich theorem.
• We also proved an important limit which is: $\lim_{x\rightarrow 0} \frac{\sin x}{x} = 1$
• In the next section, we will see another important limit.
No comments:
Post a Comment