In the previous section, we saw an easy method to find the derivative at a point. In this section, we will see a general form.
• The general form can be obtained using the same fig.13.30 that we saw in the previous section. All we need to do is, change 'a' to 'x'.
• The steps are the same with 'x' in place of 'a'. However, we will write all those 11 steps here:
1. In fig.13.31 below, the red curve is the graph of f(x).
 |
| Fig.13.31 |
• Two points P and Q are marked on the red curve.
(P is an arbitrary point. An arbitrary point is chosen so that, it will be applicable for all cases. The dictionary meaning of the word "arbitrary" can be seen here)
♦ A green horizontal line is drawn through P.
♦ A green vertical line is drawn through Q.
♦ These horizontal and vertical lines meet at R
• Thus we get a right triangle PQR
2. A green dashed vertical line is drawn through P.
• This vertical line meets the x-axis at (x,0)
[We are able to write "(x,0)" because, P is an arbitrary point. Since it is an arbitrary point, 'x' can be any point in the domain of f(x)]
• So we can write:
The x-coordinate of P is ‘x’.
• If the x-coordinate is ‘x’, then obviously, the y-coordinate will be f(x)
• Thus we get the coordinates of P: (x,f(x))
3. Another green dashed vertical line is drawn through R.
• This vertical line meets the x-axis at ((x+h),0)
• So we can write:
The x-coordinate of Q is ‘(x+h)’.
• If the x-coordinate is ‘(x+h)’, then obviously, the y-coordinate will be f(x+h)
• Thus we get the coordinates of Q: ((x+h),f(x+h))
4. Using the x-coordinates of P and Q, we can find the horizontal distance between P and Q.
• We get:
Horizontal distance between P and Q = [(x+h) – x] = h
• That means, the length PR = h.
5. Using the y-coordinates of P and Q, we can find the vertical distance between P and Q.
• We get:
Vertical distance between P and Q = [f(x+h) – f(x)]
• That means, the length QR = [f(x+h) – f(x)].
6. Now we have the base and altitude of the right triangle PQR.
• So we can write the slope of the line PQ.
Slope of PQ = $\frac{[f(x+h) – f(x)]}{h}$
7. If Q is brought very close to P, then the slope calculated in (6) will be the slope of the tangent at P
• For bringing Q closer to P, we must decrease the length h. When h approaches zero, Q will be very close to P.
• h must become very close to zero. At the same time, it must not become exact zero. This can be written as:
$\lim_{h\rightarrow 0} h$
8. From (5), we have the length of the altitude:
[f(x+h) – f(x)]
• When h approaches zero, the base PR will become infinitesimal.
• There will be corresponding changes in the altitude also.
• When h approaches zero, the length of the altitude can be written as: $\lim_{h\rightarrow 0} {[f(x+h) – f(x)]}$
9. So now we can write the slope of the tangent at P:
$\frac{\lim_{h\rightarrow 0} {[f(x+h) – f(x)]}}{\lim_{h\rightarrow 0} h}$
• The limit is being applied to both numerator and denominator. So this can be written in a simplified form as:
Slope of tangent at P = $\lim_{h\rightarrow 0}{\left[\frac{f(x+h) – f(x)}{h} \right]}$
10. But slope of the tangent at P is the derivative at P.
• Point P corresponds to any x in the domain.
• So we can write:
The result in (9) gives the derivative of f(x) at any x in the domain.
11. The derivative of f(x) at x is denoted as: f'(x).
• So we can write:
$$f'(x)~=~\lim_{h\rightarrow 0}{\left[\frac{f(x+h) – f(x)}{h} \right]}$$
Now we will see the same solved examples of the previous section:
Solved example 13.6
Find the derivative of f(x) = 3x.
Solution:
• In our present case, f(x) = 3x. So we get:
$\begin{array}{ll}
{}&{f'(x)}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{f(x+h) – f(x)}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{3(x+h) – 3 x}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{3x + 3h – 3x}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{3h}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {3 \lim_{h\rightarrow 0}{\left[\frac{h}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {3 \lim_{h\rightarrow 0}{1}}
&{} \\
{}&{}
& {~=~}& {3 × 1}
&{} \\
{}&{}
& {~=~}& {3}
&{} \\
\end{array}$
Solved example 13.7
Find the derivative of f(x) = 2x2 + 3x - 5. Also prove that f'(0) + 3f'(-1) = 0
Solution:
Part (i):
• In our present case, f(x) = 2x2 + 3x - 5. So we get:
$\begin{array}{ll}
{}&{f'(x)}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{f(x+h) – f(x)}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{[2(x+h)^2 + 3(x+h) - 5] – [2×(x)^2 + 3 x ~- 5]}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{[2(x^2 + 2hx + h^2) + 3x +3h - 5] – [2 x^2 + 3x - 5]}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{2x^2 + 4hx + 2h^2 + 3x + 3h - 5 – 2 x^2 - 3x + 5}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{4hx + 2h^2 + 3h}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{h(2h +4x + 3)}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{[2h + 4x +3]}}
&{} \\
{}&{}
& {~=~}& {4x + 3}
&{} \\
\end{array}$
Part (ii):
1. We have: f'(x) = 4x + 3
2. Thus we get: f'(0) = [4(0) + 3] = 3
3. Also we get: f'(-1) = [4(-1) + 3] = [-4 + 3] = -1
4. So f'(0) + 3f'(-1) = [3 + 3(-1)] = [3 - 3] = 0
◼ A graphical description can be written in 3 steps:
1. In the fig.13.32 below, f(x) = 2x2 + 3x - 5 is plotted in red color.
 |
| Fig.13.32 |
2. We saw that: f'(0) = 3
• That means, the "derivative of f(x)" at (x = 0) is 3.
♦ That means, slope of the tangent at (x = 0) is 3.
• When (x=0), f(x) is -5.
♦ So we mark the point (0,-5)
• If we have a point and the slope, we can draw a line through that point (recall the slope-point form that we saw in coordinate geometry lessons).
• So we draw a line through (0,-5) at a slope of 3.
♦ This line will be the tangent of f(x) at (x=0).
♦ This tangent is shown in green color.
3. We saw that: f'(-1) = -1
• That means, the "derivative of f(x)" at (x = -1) is -1.
♦ That means, slope of the tangent at (x = -1) is -1.
• When (x=-1), f(x) is -6.
♦ So we mark the point (-1,-6)
•
If we have a point and the slope, we can draw a line through that point
(recall the slope-point form that we saw in coordinate geometry
lessons).
• So we draw a line through (-1,-5) at a slope of -1.
♦ This line will be the tangent of f(x) at (x=-1).
♦ This tangent is shown in white color.
Solved example 13.8
Find the derivative of sin x
Solution:
• In our present case, f(x) = sin x. So we get:
$\begin{array}{ll}
{}&{f'(x)}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{f(x+h) – f(x)}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{[\sin (x+h)] – [sin x]}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{[\sin x \cos h ~+~\cos x \sin h] – [sin x]}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{\sin x (\cos h - 1)~+~ \cos x \sin h}{h} \right]}}
&{} \\
{}&{}
&
{~=~}& {\lim_{h\rightarrow 0}{\left[\frac{\sin x (\cos h - 1)}{h}
\right]}~+~\lim_{h\rightarrow 0}{\left[\frac{\cos x \sin h}{h} \right]}}
&{} \\
{}&{}
&
{~=~}& {\sin x \lim_{h\rightarrow 0}{\left[\frac{\cos h - 1}{h}
\right]}~+~\cos x \lim_{h\rightarrow 0}{\left[\frac{\sin h}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\sin x × 0~+~\cos x × 1}
&{} \\
{}&{}
& {~=~}& {\cos x}
&{} \\
\end{array}$
◼ Let us find the derivatives at some convenient points:
• We have: f'(x) = cos x
• Let us find the derivative at (x = 0) and $\rm{\left(x = \frac{\pi}{3} \right)}$. We get:
♦ f'(0) = cos 0 = 1
♦ $\rm{f' \left(\frac{\pi}{3}\right)~=~\cos \left(\frac{\pi}{3}\right)~=~\frac{1}{2}}$
◼ A graphical description can be written in 3 steps:
1. In the fig.13.33 below, f(x) = sin x is plotted in red color.
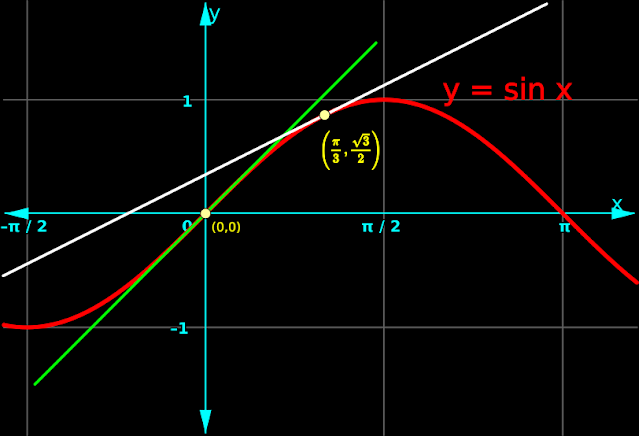 |
| Fig.13.33 |
2. We saw that: f'(0) = 1
• That means, the "derivative of f(x)" at (x = 0) is 1.
♦ That means, slope of the tangent at (x = 0) is 1.
• When (x=0), f(x) is sin 0 = 0.
♦ So we mark the point (0,0)
•
If we have a point and the slope, we can draw a line through that point
(recall the slope-point form that we saw in coordinate geometry
lessons).
• So we draw a line through (0,0) at a slope of 1.
♦ This line will be the tangent of f(x) at (x=0).
♦ This tangent is shown in green color.
3. We saw that: $\rm{f' \left(\frac{\pi}{3}\right)~=~\frac{1}{2}}$
• That means, the "derivative of f(x)" at $\rm{\left(x = \frac{\pi}{3} \right)}$ is $\frac{1}{2}$
♦ That means, slope of the tangent at $\rm{\left(x = \frac{\pi}{3} \right)}$ is $\frac{1}{2}$.
• When $\rm{\left(x = \frac{\pi}{3} \right)}$, f(x) is $\frac{\sqrt3}{2}$.
♦ So we mark the point $\rm{\left(\frac{\pi}{3}, \frac{\sqrt3}{2} \right)}$
•
If we have a point and the slope, we can draw a line through that point
(recall the slope-point form that we saw in coordinate geometry
lessons).
• So we draw a line through $\rm{\left(\frac{\pi}{3}, \frac{\sqrt3}{2} \right)}$ at a slope of $\frac{1}{2}$.
♦ This line will be the tangent of f(x) at $\rm{\left(x = \frac{\pi}{3} \right)}$.
♦ This tangent is shown in white color.
Solved example 13.9
Find the derivative of f(x) = 3. Also find f'(0) and f'(3).
Solution:
Part (i):
• In our present case, f(x) = 3. So we get:
$\begin{array}{ll}
{}&{f'(0)}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{f(x+h) – f(x)}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{[3] – [3]}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{0}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {0}
&{} \\
\end{array}$
Part (ii):
1. We have: f'(x) = 0. This is a constant function.
• So f'(0) = 0.
2. We have: f'(x) = 0. This is a constant function.
• So f'(3) = 0.
◼ In this example, we see that:
♦ f’(0) = 0
♦ f’(3) = 0
• In fact, we can put any value for a. The derivative will be zero.
• The reason can be written in 2 steps:
1. f(x) = 3 is a constant function.
• That means, whatever be the value of x, the resulting f(x) will be the same.
• If there is no change in f(x), it means that, there is no rate of change.
♦ That means, rate of change is zero.
♦ That means, derivative is zero.
2. We can think in terms of slope of tangent also.
• For a straight line, the tangent at any point, will be the line itself.
• Here, the straight line is horizontal. So the tangent at any point will also be horizontal.
• For a horizontal line, the slope is zero.
• For a given function f, we can find the derivative at every point. The derivative will be a new function denoted by f'.
• In some cases, the derivative will be a constant function.
♦ The derivative in solved example 13.6 above is a constant function.
♦ The derivative in solved example 13.9 above is a constant function.
• In some cases, the derivative will be an ordinary function.
♦ The derivative in solved example 13.7 above is an ordinary function.
♦ The derivative in solved example 13.8 above is an ordinary function.
◼ Derivative can be denoted in different ways. In the discussions above, we denoted it as f'(x)
• Five more methods are given below:
1. Derivative can be denoted as $\frac{d}{dx}\left(f(x) \right)$.
2. If y = f(x), then the derivative can be denoted as $\frac{dy}{dx}$.
• We can read it in any one of the two ways below:
(i) Derivative of y with respect to x.
(ii) "dy" by "dx"
3. Derivative can be denoted as : $D \left(f(x) \right)$.
4. Derivative of f(x) at (x=a) can be denoted in any one of the three ways below:
(i) $\left.\frac{d}{dx} f(x)\right\vert_{a}$
(ii) $\left.\frac{df}{dx}\right\vert_{a}$
(iii) $\left(\frac{df}{dx}\right)_{x=a}$
In the next section, we will see a few more solved examples.
No comments:
Post a Comment