Chapter 11.4 - Ellipse

In the previous section, we completed a discussion on parabola. In this section, we will see ellipse.

Some basics about ellipse can be written in 6 steps:
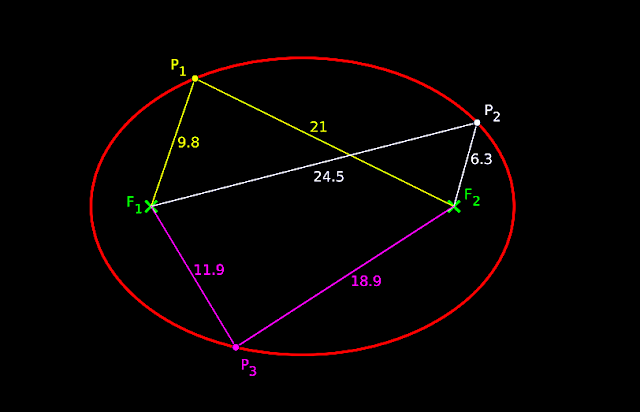
1. Consider the five points F₁, F₂, P₁, P₂ and P₃ marked in fig.11.29 below:

Fig.11.29

2. Let us write some distances:
• Distance of P₁:
   ♦ Distance of P₁ from F₁ is 9.8 units.
   ♦ Distance of P₁ from F₂ is 21 units.
         ✰ The sum of the two distances is (9.8+21) = 30.8 units.
• Distance of P₂:
   ♦ Distance of P₂ from F₁ is 24.5 units.
   ♦ Distance of P₂ from F₂ is 6.3 units.
         ✰ The sum of the two distances is (24.5+6.3) = 30.8 units.
• Distance of P₃:
   ♦ Distance of P₃ from F₁ is 11.9 units.
   ♦ Distance of P₃ from F₂ is 18.9 units.
         ✰ The sum of the two distances is (11.9+18.9) = 30.8 units.
3. So the three points P₁, P₂ and P₃ have a specialty. It can be written in two steps:
(i) Take any one of those three points.
   ♦ Measure the distance of that point from F₁.
   ♦ Measure the distance of that point from F₂.
(ii) The sum of the two distances will be 30.8 units.
4. There are infinite number of points for which the sum is 30.8 units.      
• All such points will lie in the red curve.
• The red curve is called an ellipse.
5. So we can write the definition:
An ellipse is the set of all points in a plane sum of whose distances from two fixed points in the plane is a constant.
6. Note that, for a particular ellipse, the two points F₁ and F₂ are fixed. If we change one or both of those points, we will get another ellipse.

---

Now we will see some basic features of ellipse. They can be written in 7 steps:
1. We have seen that, F₁ and F₂ are two fixed points.
• They are called the foci of the ellipse.
(‘foci’ is the plural of ‘focus’)
2. Draw a line connecting the two foci. Extend this line in both directions.
• Let it intersect the ellipse at A and B.
• Then the line segment AB is called the major axis of the ellipse.
• This is shown in fig.11.30 below:

Fig.11.30

3. The midpoint of F₁F₂ is called center of the ellipse. It is denoted by the letter O.
4. Draw a line through O and perpendicular to AB.
• Let this line intersect the ellipse at C and D
• Then the line segment CD is called the minor axis of the ellipse.
5. The end points A and B of the major axis are called vertices of the ellipse.
6. The length of the major axis is written as ‘2a’. This is shown in fig.11.31 below:

Fig.13.31

• The length of the minor axis is written as ‘2b’
• The distance between the two foci is written as ‘2c’
7. Based on the above fig.11.31, we can write:
   ♦ Length of semi major axis is ‘a’.   
   ♦ Length of semi minor axis is ‘b’.    
   ♦ Distance from center to any one focus is 'c'.

---

Now we will derive the relation between 'a', 'b' and 'c'. It can be derived in four steps:
1. In fig.12.32 below, B and C are two points on the ellipse.
2. Let us write the distances related to B:
• Distance of B from F₁ can be written as:

$\begin{array}{ll}
{}&{BF_1}
& {~=~}& {OF_1}
&{~+~}&{OF_2}&{~+~}&{B F_2} \\

{}&{}
& {~=~}& {c}
&{~+~}&{c}&{~+~}&{OB - OF_2} \\

{}&{}
& {~=~}& {c}
&{~+~}&{c}&{~+~}&{a - c} \\

{}&{}
& {~=~}& {c}
&{}&{}&{~+~}&{a} \\

\end{array}$

• Distance of B from F₂ can be written as:

$\begin{array}{ll}
{}&{BF_2}
& {~=~}& {OB}
&{~-~}&{OF_2}&{}&{} \\

{}&{}
& {~=~}& {a}
&{~-~}&{c}&{}&{} \\

\end{array}$

• So sum of the two distances = (c+a) + (a-c) = 2a

3. Let us write the distances related to C.
• Distance of C from F₁ can be written as:

$\begin{array}{ll}
{}&{CF_1}
& {~=~}& {\sqrt{(O F_1)^2 ~+~(OC)^2}}
&{}&{}&{}&{} \\

{}&{}
& {~=~}& {\sqrt{c^2 ~+~b^2}}
&{}&{}&{}&{} \\

\end{array}$

• Distance of C from F₂ can be written as:

$\begin{array}{ll}
{}&{CF_2}
& {~=~}& {\sqrt{(O F_2)^2 ~+~(OC)^2}}
&{}&{}&{}&{} \\

{}&{}
& {~=~}& {\sqrt{c^2 ~+~b^2}}
&{}&{}&{}&{} \\

\end{array}$

• So sum of the two distances
= $\sqrt{c^2 ~+~b^2} + \sqrt{c^2 ~+~b^2}~=~2 \sqrt{c^2 ~+~b^2}$

4. Both B and C are points on the same ellipse. So we can equate the sum of the distances. We get:

$\begin{array}{ll}
{}&{2a}
& {~=~}& {2\sqrt{c^2 ~+~b^2}}
&{}&{}&{}&{} \\

{\Rightarrow}&{a}
& {~=~}& {\sqrt{c^2 ~+~b^2}}
&{}&{}&{}&{} \\

{\Rightarrow}&{a^2}
& {~=~}& {b^2 ~+~c^2}
&{}&{}&{}&{} \\

\end{array}$

• This is a simple relation between 'a', 'b' and 'c'.

---

The relation a² = b² + c² is applicable to any ellipse. Let us see two cases where this relation gives interesting results.

Case 1: Special case of an ellipse where it becomes a circle.
This can be written in five steps:
1. Suppose that, the vertices A and B are fixed in position.
    ♦ When A and B are fixed, the length 2a becomes a constant.
    ♦ When 2a is a constant, ‘a’ is a constant.
2. Keeping ‘a’ constant, we decrease ‘c’.
• We have the relation: a² = b² + c².
• So, keeping ‘a’ constant, if we decrease ‘c’, The length ‘b’ will automatically increase.
3. An increase in ‘b’ is an increase in the length of minor axis.
• As the length of the minor axis increase, the shape of the ellipse will become more and more circular.
• This is shown in the animation below:

Fig.13.32

4. We are decreasing ‘c’.
• That means, the foci get closer and closer to O.
• Finally, when ‘c’ becomes zero, the foci will merge at the center O.
• In such a situation, ‘a’ and ‘b’ are equal. The ellipse has become a circle.
5. So we can write:
A circle is an ellipse with a = b and c = 0.

Case 2: Special case of an ellipse where it becomes a line.
This can be written in five steps:
1. Suppose that, the vertices A and B are fixed in position.
    ♦ When A and B are fixed, the length 2a becomes a constant.
    ♦ When 2a is a constant, ‘a’ is a constant.
2. Keeping ‘a’ constant, we increase ‘c’.
• We have the relation: a² = b² + c².
• So, keeping ‘a’ constant, if we increase ‘c’, The length ‘b’ will automatically decrease.
3. A decrease in ‘b’ is a decrease in the length of minor axis.
• As the length of the minor axis decrease, the shape of the ellipse will become more and more linear.
• This is shown in the animation below:

Fig.11.33

4. We are increasing ‘c’.
• That means, the foci get closer and closer to vertices A and B.
• Finally, when ‘c’ becomes 'a', the foci will merge with A and B.
• In such a situation, ‘b’ is zero. The ellipse has become a line.
5. So we can write:
A line is an ellipse with a = c and b = 0.

---

Eccentricity of an Ellipse

This can be explained in 5 steps:
1. Consider the distance ‘c’.
• It is the distance of the focus from the center O.
2. Consider the distance ‘a’.
• It is the distance of the vertex from the center O.
3. Eccentricity of an ellipse is the ratio of the above two items. It is denoted by the letter ‘e’.
So we can write: $\rm{e=\frac{c}{a}}$
4. Based on this result, we can write: c = ae.
• That means, in any ellipse, the focus is at a distance of ae from the center.
5. We have seen that, for a circle, a = c
• So for a circle, c = ce, which gives e = 1
• We can write:
For a circle, eccentricity is 1

---

In the next section, we will see the standard equations of an ellipse.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com