In the previous section, we saw the basic details about parabolas. In this section, we will see the latus rectum of a parabola.
Latus rectum of a parabola
This can be explained in three steps:
1. Latus rectum is a line segment.
2. If a line segment is to qualify as the latus rectum of a parabola, it must satisfy three conditions.
(i) It must pass through F.
(ii) It must be perpendicular to the axis.
(iii) It’s end points must lie on the parabola.
3. Line segment AB in fig.11.23 below satisfies all three conditions. So it is the latus rectum of that parabola.
 |
| Fig.11.23 |
Length of the latus rectum
• We have seen the four cases where the equation of parabola is in the simplest form. Length of the latus rectum can be calculated very easily in those four cases.
• Let us see case A. We want the length AB. It can be calculated in 5 steps:
1. In the fig.11.23 above, a perpendicular is drawn from A to the directrix. C is the foot of the perpendicular.
2. Consider the quadrilateral ACDF. We must prove that, ACDF is a rectangle. The proof can be written in 5 steps:
(i) We know that the directrix is perpendicular to axis. So ∠CDF = 90o
(ii) We know that latus rectum is perpendicular to the axis. So ∠AFD = 90o
(iii) We have drawn AC perpendicular to the directrix. So ∠ACD = 90o
(iv) The sum of all interior angles of a quadrilateral is 360o. Here we have calculated the value of three interior angles. Each of them are 90o. So the fourth angle ∠CAF must also be 90o
(v) Since all four interior angles are 90o, the quadrilateral ACDF is a rectangle.
3. In a rectangle, opposite sides are equal. So AC must be equal to DF
• But DF = (DV + VF) = (a+a) = 2a
• So AC = DF = 2a
4. Point A is on the parabola. It is equidistant from the directrix and F
• So AC = AF
• Thus we get, AF = AC = 2a
5. The parabola is symmetrical about it’s axis. So length BF will be equal to length AF
• So we get: AB = (AF + BF) = (AF + AF) = 2AF = 2 × 2a = 4a
• Let us see case C. It is shown in fig.11.24 below:
 |
| Fig.11.24 |
• We want the length AB. It can be calculated in 5 steps:
1. In the fig.11.24 above, a perpendicular is drawn from A to the directrix. C is the foot of the perpendicular.
2. Consider the quadrilateral ACDF. We must prove that, ACDF is a rectangle. The proof can be written in 5 steps:
(i) We know that the directrix is perpendicular to axis. So ∠CDF = 90o
(ii) We know that latus rectum is perpendicular to the axis. So ∠AFD = 90o
(iii) We have drawn AC perpendicular to the directrix. So ∠ACD = 90o
(iv)
The sum of all interior angles of a quadrilateral is 360o. Here we
have calculated the value of three interior angles. Each of them are
90o. So the fourth angle ∠CAF must also be 90o
(v) Since all four interior angles are 90o, the quadrilateral ACDF is a rectangle.
3. In a rectangle, opposite sides are equal. So AC must be equal to DF
• But DF = (DV + VF) = (a+a) = 2a
• So AC = DF = 2a
4. Point A is on the parabola. It is equidistant from the directrix and F
• So AC = AF
• Thus we get, AF = AC = 2a
5. The parabola is symmetrical about it’s axis. So length BF will be equal to length AF
• So we get: AB = (AF + BF) = (AF + AF) = 2AF = 2 × 2a = 4a
• In all four cases, we will find that, length of latus rectum is 4a. Where 'a' is the distance of F from V.
• The reader may write the steps for case B and case D.
Now we will see some solved examples:
Solved example 11.5
For the parabola y2 = 8x, write the following items:
(i) Coordinates of the focus
(ii) Equation of the axis
(iii) Equation of the directrix
(iv) Length of the latus rectum.
Solution:
1. Consider the chart that we saw in fig.11.22 of the previous section. It is shown again below:
 |
| Fig.11.22 |
• In our present case, the given equation falls in the category y2 = 4ax.
• So we can write:
The axis of the given parabola coincides with the x-axis. And also, the given parabola opens to the right.
2. Comparing y2 = 4ax and the given equation y2 = 8x, we get:
8 = 4a which gives a = 2
3. Based on the information in the above two steps, we can write:
Focus F lies on the +ve side of the x-axis. It lies at a distance of a = 2 from the origin.
• So the coordinates of F are: (2,0)
• This is the answer for part (i).
4. The axis of the given parabola coincides with the x-axis.
• So equation of the axis of the parabola is: y = 0
• This is the answer for part (ii)
5. The directrix is perpendicular to the x-axis. So it will be parallel to the y-axis.
• The directrix intersects the x-axis at a point a = 2 units away from the origin.
♦ This point of intersection will be on the -ve side of the x-axis.
♦ So the equation of the directrix will be x = -2.
• This is the answer for part (iii)
6. The length of the latus rectum will be 4a, which gives 4 × 2 = 8 units.
• This is the answer for part (iv)
7. The actual plot is shown below:
 |
| Fig.11.25 |
Solved example 11.6
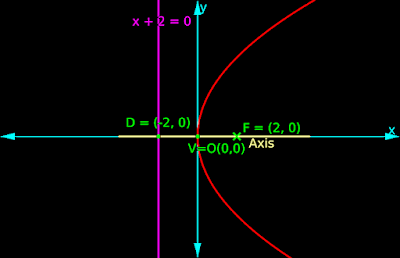
Find the equation of the parabola with focus (2,0) and directrix x = -2
Solution:
1. Given that, the focus is (2,0).
•
So the axis of the parabola passes through (2,0).
•
But using this information, we cannot decide about the direction of the axis of the parabola.
2. To help us decide about the direction of the axis, we are given the equation of the directrix. The equation is: x = -2
•
Based on this equation, we can write:
Directrix is a vertical line. It passes through (-2,0)
3. If the directrix is a vertical line, the axis of the parabola will be a horizontal line.
•
A horizontal line passing through (2,0) is the x-axis itself.
•
So we can write:
The axis of the parabola coincides with the x-axis.
•
Now we can draw a rough sketch as shown below:
 |
| Fig.11.26 |
•
Based on the rough sketch and the chart in fig.11.22, we can write:
The equation of the parabola will be in the form: y2 = 4ax
4. So our next aim is to find ‘a’.
•
The value of ‘a’ can be calculated in any of the two ways:
(i) ‘a’ is the distance DV, which is 2
(ii) ‘a’ is the distance FV, which is 2
5. So the equation of the parabola is:
y2 = 4 × 2 × x
⇒ y2 = 8x
Solved example 11.7
Find the equation of the parabola with vertex at (0,0) and focus at (0,2)
Solution:
1. Given that, the focus is (2,0).
•
So the axis of the parabola passes through (2,0).
•
But using this information, we cannot decide about the direction of the axis.
2. To help us decide about the direction of the axis, we are given the coordinates of the vertex. The coordinates are: (0,0)
•
The axis of the parabola is a line which passes through both vertex and focus.
•
A line which passes through (0,0) and (2,0) is the x-axis.
•
So we can write:
The axis of the parabola coincides with the x-axis.
3. So we have V, F and the axis. We can draw a rough sketch as shown in fig.11.27 below:
 |
| Fig.11.27 |
• Based on the rough sketch and the chart in fig.11.22, we can write:
The equation of the parabola will be in the form: y2 = 4ax
4. So our next aim is to find ‘a’.
• ‘a’ is the distance DV, which is 2
5. So the equation of the parabola is:
y2 = 4 × 2 × x
⇒ y2 = 8x
Solved example 11.8
Find the equation of the parabola which passes through (2,-3) if it is symmetric about the y-axis and it’s vertex is at the origin.
Solution:
1. The given parabola satisfies two conditions:
(i) It is symmetric about one of the coordinate axes.
(ii) It’s vertex is at the origin.
•
So this parabola is one of the four simplest forms.
2. This parabola is symmetric about the y-axis.
•
So based on the chart in fig.11.22, we can write:
The equation will be one of the two below:
(i) x2 = 4ay (opening upwards)
(ii) x2 = -4ay (opening downwards)
3. Given that, the parabola passes through (2,-3)
•
The point (2,-3) lies in the fourth quadrant. So the parabola opens downwards.
•
So we can write:
The equation is in the form x2 = -4ay
4. Given that, the parabola passes through (2,-3)
•
Substituting these coordinates in the equation obtained in (3), we get:
22 = -4 × a × -3
a = 1/3
5. So equation of the parabola is:
$\begin{array}{ll}
{}&{x^2}
&{}={}& {-4 \times \left(\frac{1}{3} \right) \times x}
&{} \\
{\Rightarrow}&{x^2}
&{}={}& {\frac{-4x}{3}}
&{} \\
\end{array}$
6. The actual plot is shown below:
 |
| Fig.11.28 |
Link to a few more solved examples is given below:
In the next section, we will see latus rectum.
No comments:
Post a Comment