In the previous section, we saw the details about circles. In this section, we will see the details about parabolas.
Some basics about parabola can be written in 9 steps:
1. Consider the point P1 in fig.11.15 below:
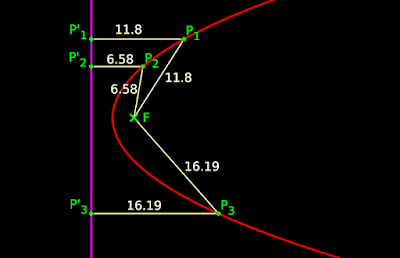 |
| Fig.11.15 |
• This point P1 satisfies one condition. It can be written in three steps:
(i) The distance of P1 from the magenta line is P1P’1
(Remember that, the distance of a point from a line should be measured in the perpendicular direction. That is., the line segment P1P’1 must be perpendicular to the magenta line.)
(ii) The distance of P1 from the point F is FP1
(iii) The condition is that, the above two distances are equal.
• That is., P1P’1 = FP1
♦ In the fig., both distances are 11.8 units
2. Consider the point P2 in the fig.11.15.
This point P2 satisfies one condition. It can be written in steps:
(i) The distance of P2 from the magenta line is P2P’2
(ii) The distance of P2 from the point F is FP2
(iii) The condition is that, the above two distances are equal.
• That is., P2P’2 = FP2
♦ In the fig., both distances are 6.58 units
3. Consider the point P3 in the fig.11.15.
This point P3 satisfies one condition. It can be written in steps:
(i) The distance of P3 from the magenta line is P3P’3
(ii) The distance of P3 from the point F is FP3
(iii) The condition is that, the above two distances are equal.
• That is., P3P’3 = FP3
♦ In the fig., both distances are 16.19 units
4. We have seen three points. All of them satisfy the same condition:
♦ Distance from the magenta line
♦ is equal to
♦ Distance from F
5. There are infinite number of points which will satisfy the above condition. All such points will lie on the red curve.
• The red curve is called Parabola.
◼ We can write:
• A parabola is the set of all points that are equidistant from a fixed line and a fixed point.
♦ The fixed point must not be on the fixed line.
♦ The fixed line, fixed point and all points on the parabola, must lie on the same plane.
✰ The fixed line is called the directrix (l) of the parabola.
✰ The fixed point is called the focus (F) of the parabola.
6. We can draw a line in such a way that:
♦ The line passes through the focus F
♦ The line is perpendicular to the directrix.
• Only one line is possible which satisfies both the conditions. That line is called the axis of the parabola.
• It is shown in fig.11.16 below:
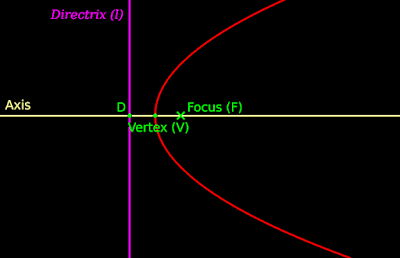 |
| Fig.11.16 |
7. Consider the point where the axis intersects the parabola. That point is called the vertex (V) of the parabola. It is shown in fig.11.16 above.
8. Consider the point where the axis intersects the directrix. That point is marked as D in the above fig.11.16.
• Let us see the significance of point D. It can be written in four steps:
(i) We know that, all points on the parabola are equidistant from l and F
(ii) V is a point on the parabola. So V is also equidistant from l and F
(iii) That means, V is the midpoint of DF
(iv) In other words:
♦ Distance of l from V
♦ is equal to
♦ Distance of F from V
9. Let us see how the word parabola is derived:
♦ The word ‘para’ means ‘for’
♦ The word ‘bola’ means ‘throwing’
• In projectile motion in physics classes, we have seen that, a thrown object follows a parabolic path.
Standard equations of parabola
• The equation of a parabola will be in the simplest form when two conditions are satisfied:
(i) V is at the origin of the coordinate axes.
(ii) Axis of the parabola coincides with one of the coordinate axes.
• Based on this information, we can think of four cases:
A. V is at the origin, axis coincides with the x-axis and parabola opens to the right.
♦ This is shown in fig.11.17(a) below.
✰ Axes are shown in cyan color
✰ Parabola is shown in red color.
✰ Directrix is shown in magenta color. It is marked as l.
✰ Axis of the parabola is shown in yellow color.
B. V is at the origin, axis coincides with the x-axis and parabola opens to the left.
♦ This is shown in fig.11.17(b) below.
C. V is at the origin, axis coincides with the y-axis and parabola opens upwards.
♦ This is shown in fig.11.17(c) below.
D. V is at the origin, axis coincides with the y-axis and parabola opens downwards.
♦ This is shown in fig.11.17(d) below.
 |
| Fig.11.17 |
• We will now derive equation in each case.
Case A:
V is at the origin, axis coincides with the x-axis and parabola opens to the right.
• This can be written in 6 steps:
1. Let the focus F be at a distance of ‘a’ units from the vertex V.
• This is shown in fig.11.18 below:
 |
| Fig.11.18 |
(i) Axis of the parabola coincides with the x-axis. So F lies on the x-axis.
(ii) V is at the origin O
• Based on these two points, we can write:
Coordinates of F are (a,0)
2. Remember that, D and F are equidistant from V.
• So the coordinates of D will be (-a,0)
3. Mark any convenient point P(x,y) on the parabola.
• Draw a perpendicular from P onto the directrix l
• Let the foot of the perpendicular be P1
4. Let us write the coordinates of P1:
• P1 and D lies on the same vertical line.
♦ So both will have the same x-coordinate ‘-a’
• P1 and P lies on the same horizontal line.
♦ So both will have the same y-coordinate ‘y’
• Thus the coordinates of P1 are: (-a,y)
5. Now we have the coordinates of all the points. We can calculate the distances:
• First we calculate PP1:
$\begin{array}{ll}
{}&{PP_1}
&{}={}& {\sqrt{(-a - x)^2~+~(y-y)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{[-1 × (a + x)]^2~+~(y-y)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{(a + x)^2}}
&{} \\
\end{array}$
• Next we calculate PF:
$\begin{array}{ll}
{}&{PF}
&{}={}& {\sqrt{(a - x)^2~+~(0-y)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{(a - x)^2~+~y^2}}
&{} \\
\end{array}$
6. Remember that, any point on the parabola is equidistant from F and l.
• So we can equate the above two distances. We get:
$\begin{array}{ll}
{}&{PP_1}
& {~=~}& {PF}
&{}&{}&{} \\
{\Rightarrow}&{\sqrt{(a + x)^2}}
& {~=~}& {\sqrt{(a - x)^2~+~y^2}}
&{}&{}&{} \\
{\Rightarrow}&{(a + x)^2}
& {~=~}& {(a - x)^2~+~y^2}
&{}&{}&{} \\
{\Rightarrow}&{a^2 + 2ax + x^2}
& {~=~}& {a^2 - 2ax + x^2~+~y^2}
&{}&{}&{} \\
{\Rightarrow}&{2ax}
& {~=~}& {- 2ax + y^2}
&{}&{}&{} \\
{\Rightarrow}&{y^2}
& {~=~}& {4ax}
&{}&{}&{} \\
\end{array}$
• This is the equation of the parabola for case A.
Case B:
V is at the origin, axis coincides with the x-axis and parabola opens to the left.
• This can be written in 6 steps:
1. Let the focus F be at a distance of ‘a’ units from the vertex V.
• This is shown in fig.11.19 below:
 |
| Fig.13.19 |
• Remember the two points:
(i) Axis of the parabola coincides with the x-axis. So F lies on the x-axis.
(ii) V is at the origin O
• Based on these two points, we can write:
Coordinates of F are (-a,0)
2. Remember that, D and F are equidistant from V.
• So the coordinates of D will be (a,0)
3. Mark any convenient point P(x,y) on the parabola.
• Draw a perpendicular from P onto the directrix l
• Let the foot of the perpendicular be P1
4. Let us write the coordinates of P1:
• P1 and D lies on the same vertical line.
♦ So both will have the same x-coordinate ‘a’
• P1 and P lies on the same horizontal line.
♦ So both will have the same y-coordinate ‘y’
• Thus the coordinates of P1 are: (a,y)
5. Now we have the coordinates of all the points. We can calculate the distances:
• First we calculate PP1:
$\begin{array}{ll}
{}&{PP_1}
&{}={}& {\sqrt{(a - x)^2~+~(y-y)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{(a - x)^2}}
&{} \\
\end{array}$
• Next we calculate PF:
$\begin{array}{ll}
{}&{PF}
&{}={}& {\sqrt{(-a - x)^2~+~(0-y)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{[-1 × (a + x)]^2~+~y^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{(a + x)^2~+~y^2}}
&{} \\
\end{array}$
6. Remember that, any point on the parabola is equidistant from F and l.
• So we can equate the above two distances. We get:
$\begin{array}{ll}
{}&{PP_1}
& {~=~}& {PF}
&{}&{}&{} \\
{\Rightarrow}&{\sqrt{(a - x)^2}}
& {~=~}& {\sqrt{(a + x)^2~+~y^2}}
&{}&{}&{} \\
{\Rightarrow}&{a^2 - 2ax + x^2}
& {~=~}& {a^2 + 2ax + x^2~+~y^2}
&{}&{}&{} \\
{\Rightarrow}&{-2ax}
& {~=~}& {2ax + y^2}
&{}&{}&{} \\
{\Rightarrow}&{y^2}
& {~=~}& {-4ax}
&{}&{}&{} \\
\end{array}$
• This is the equation of the parabola for case B.
Case C:
V is at the origin, axis coincides with the y-axis and parabola opens upwards.
• This can be written in 6 steps:
1. Let the focus F be at a distance of ‘a’ units from the vertex V.
• This is shown in fig.11.20 below:
 |
| Fig.11.20 |
(i) Axis of the parabola coincides with the y-axis. So F lies on the y-axis.
(ii) V is at the origin O
• Based on these two points, we can write:
Coordinates of F are (0,a)
2. Remember that, D and F are equidistant from V.
• So the coordinates of D will be (0,-a)
3. Mark any convenient point P(x,y) on the parabola.
• Draw a perpendicular from P onto the directrix l
• Let the foot of the perpendicular be P1
4. Let us write the coordinates of P1:
• P1 and D lies on the same horizontal line.
♦ So both will have the same y-coordinate ‘-a’
• P1 and P lies on the same vertical line.
♦ So both will have the same x-coordinate ‘x’
• Thus the coordinates of P1 are: (x,-a)
5. Now we have the coordinates of all the points. We can calculate the distances:
• First we calculate PP1:
$\begin{array}{ll}
{}&{PP_1}
&{}={}& {\sqrt{(x - x)^2~+~(-a-y)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{[-1 × (a + y)]^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{(a + y)^2}}
&{} \\
\end{array}$
• Next we calculate PF:
$\begin{array}{ll}
{}&{PF}
&{}={}& {\sqrt{(0 - x)^2~+~(a-y)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{x^2~+~(a-y)^2}}
&{} \\
\end{array}$
6. Remember that, any point on the parabola is equidistant from F and l.
• So we can equate the above two distances. We get:
$\begin{array}{ll}
{}&{PP_1}
& {~=~}& {PF}
&{}&{}&{} \\
{\Rightarrow}&{\sqrt{(a + y)^2}}
& {~=~}& {\sqrt{x^2~+~(a-y)^2}}
&{}&{}&{} \\
{\Rightarrow}&{a^2 + 2ay + y^2}
& {~=~}& {x^2 ~+~ a^2 - 2ay + y^2}
&{}&{}&{} \\
{\Rightarrow}&{2ay}
& {~=~}& {x^2 - 2ay}
&{}&{}&{} \\
{\Rightarrow}&{x^2}
& {~=~}& {4ay}
&{}&{}&{} \\
\end{array}$
• This is the equation of the parabola for case C.
Case D:
V is at the origin, axis coincides with the y-axis and parabola opens downwards.
• This can be written in 6 steps:
1. Let the focus F be at a distance of ‘a’ units from the vertex V.
• This is shown in fig.11.21 below:
 |
| Fig.11.21 |
(i) Axis of the parabola coincides with the y-axis. So F lies on the y-axis.
(ii) V is at the origin O
• Based on these two points, we can write:
Coordinates of F are (0,-a)
2. Remember that, D and F are equidistant from V.
• So the coordinates of D will be (0,a)
3. Mark any convenient point P(x,y) on the parabola.
• Draw a perpendicular from P onto the directrix l
• Let the foot of the perpendicular be P1
4. Let us write the coordinates of P1:
• P1 and D lies on the same horizontal line.
♦ So both will have the same y-coordinate ‘a’
• P1 and P lies on the same vertical line.
♦ So both will have the same x-coordinate ‘x’
• Thus the coordinates of P1 are: (x,a)
5. Now we have the coordinates of all the points. We can calculate the distances:
• First we calculate PP1:
$\begin{array}{ll}
{}&{PP_1}
&{}={}& {\sqrt{(x - x)^2~+~(a-y)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{(a - y)^2}}
&{} \\
\end{array}$
• Next we calculate PF:
$\begin{array}{ll}
{}&{PF}
&{}={}& {\sqrt{(0 - x)^2~+~(-a-y)^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{x^2~+~[-1 × (a+y)]^2}}
&{} \\
{}&{}
&{}={}& {\sqrt{x^2~+~(a+y)^2}}
&{} \\
\end{array}$
6. Remember that, any point on the parabola is equidistant from F and l.
• So we can equate the above two distances. We get:
$\begin{array}{ll}
{}&{PP_1}
& {~=~}& {PF}
&{}&{}&{} \\
{\Rightarrow}&{\sqrt{(a - y)^2}}
& {~=~}& {\sqrt{x^2~+~(a+y)^2}}
&{}&{}&{} \\
{\Rightarrow}&{a^2 - 2ay + y^2}
& {~=~}& {x^2 ~+~ a^2 + 2ay + y^2}
&{}&{}&{} \\
{\Rightarrow}&{-2ay}
& {~=~}& {x^2 + 2ay}
&{}&{}&{} \\
{\Rightarrow}&{x^2}
& {~=~}& {-4ay}
&{}&{}&{} \\
\end{array}$
• This is the equation of the parabola for case D.
So we have seen all the four cases. The results follow a pattern. So we can draw a flow chart:
 |
| Fig.11.22 |
In the next section, we will see latus rectum.
No comments:
Post a Comment