In the previous section, we completed a discussion on straight lines. In this chapter, we will see the details about curves like circles, ellipses, parabolas and hyperbolas.
First we will see a double napped right circular cone. It can be written in 5 steps:
1. In fig.11.1(a) below, l is a fixed vertical line.
• m is another line which intersects l at V.
• Also, m is inclined at an angle of 𝛼 with l.
 |
| Fig.11.1 |
2. Next step is to rotate m around l
• During the rotation,
♦ Point V must not change.
♦ The angle 𝛼 must not change.
• Such a rotation is shown in the animation in fig.11.2 below:
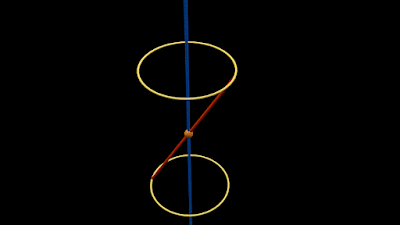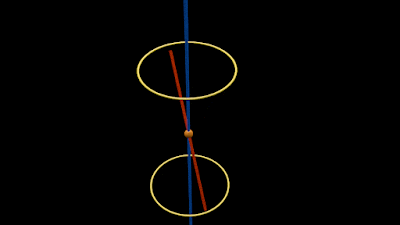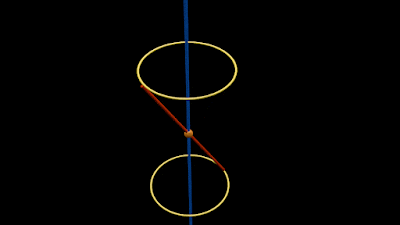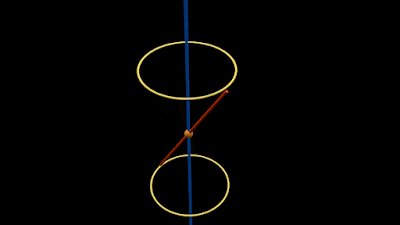 |
| Fig.11.2 |
We see that:
♦ The rotating line m generates a conical surface.
♦ The top end of m moves along the top yellow circle.
♦ The bottom end of m moves along the bottom yellow circle.
3. We get an upper nappe and a lower nappe. The yellow circles form the bases of the nappes.
• This is shown in fig.11.1(b) above. The shape in fig.11.1(b) is called a double-napped right circular cone. For our discussions in this chapter, we will call it simply as cone.
• The cone obtained in this way will be hollow.
4. Let us see the various features of a cone:
(i) The point V is called vertex of the cone.
(ii) The line l is called axis of the cone.
(iii) The line m is called generator of the cone
(iv) The vertex separates the cone into two parts called nappes.
• These features are marked in fig.11.1(c) above.
5. Keeping V and 𝛼 fixed, we can increase the lengths of l and m.
• Then the size of the cone will also increase.
• By increasing the lengths of l and m, the size of cone can be increased upto infinity.
Sections of a cone
This can be explained in 5 steps:
1. We can cut a cone using a plane. An example is shown in fig.11.3(a) below:
 |
| Fig.11.3 |
2. When such a cut is made, the cone is separated into two parts.
(i) A larger part. We will call it major part.
(ii) A smaller part. We will call it minor part.
3. After making the cut, we remove the minor part and the plane.
• After removing them, when we look at the portion where the cut is made, we will see a curve.
• This curve is called a conic section. This curve is highlighted in green color in fig.11.3(b).
◼ We can write:
Conic sections are curves obtained by intersecting a right circular cone by a plane.
4. Consider the situation in fig.11.3(a). In this situation, if we look from the edge of the plane, that edge will appear as a line. This is shown in fig.11.3(c).
• The upper and lower nappes will appear as triangles.
• The angle between the plane and the axis l is marked as 𝛽.
5. There are three ways to cut a cone.
(i) The plane can pass through the vertex.
(ii) The plane can pass through the upper nappe.
(iii) The plane can pass through the lower nappe.
• The angle 𝛽 can also vary according to the requirement.
Circle, ellipse, parabola and hyperbola as conic sections
This can be explained in 6 steps:
1. In the above fig.13.3(c), the angle 𝛽 is less than 90o.
• If 𝛽 is exactly 90o, then the plane will cut the cone in a horizontal manner. This is shown in fig.11.4(a) below:
 |
| Fig.11.4 |
• In fig.11.4(b) above, we can clearly see the major part and minor part.
• In fig.11.4(c) above, the plane and the minor part are removed to reveal the conic section.
• The conic section is highlighted in green color. It is a circle.
2. We know the significance of angle 𝛼. It is the angle between the generator m and the axis l.
• If this 𝛼 is 90o, we will not get a cone. We will get only a plane surface.
• So 𝛼 must be always less than 90o. We can write: 𝛼 < 90o
3. We have seen the situation where 𝛽 is 90o. We saw that, a circle will be obtained.
• Now we will see the situation when 𝛽 is less than 90o. For this situation, we can write: 𝛼 < 90o and 𝛽 < 90o
• Here three cases can arise:
(i) 𝛼 < 90o, 𝛽 < 90o and 𝛼 < 𝛽
(ii) 𝛼 < 90o, 𝛽 < 90o and 𝛼 = 𝛽
(iii) 𝛼 < 90o, 𝛽 < 90o and 𝛼 > 𝛽
4. An ellipse is obtained in case 3(i). It is shown in fig.11.5 below:
 |
| Fig.11.5 |
• In fig.11.5(a) above, 𝛽 is greater than 𝛼.
• In fig.(b), we can clearly see the major and minor parts.
• In fig.(c), the plane and the minor part are removed to reveal the conic section.
• The conic section is highlighted in green color. It is an ellipse.
5. A parabola is obtained in case 3(ii). It is shown in fig.11.6 below:
 |
| Fig.11.6 |
• In fig.11.6(a) above, 𝛽 is equal to 𝛼.
• In fig.(b), we can clearly see the major and minor parts.
• In fig.(c), the plane and the minor part are removed to reveal the conic section.
• The conic section is highlighted in green color. It is a parabola.
6. A hyperbola is obtained in case 3(iii). It is shown in fig.11.7 below:
 |
| Fig.11.7 |
• In fig.11.7(a) above, 𝛽 is less than 𝛼.
♦ So the plane is able to cut both upper nappe and lower nappe.
• In fig.(b), we can clearly see the major and minor parts.
• In fig.(c), the plane and the minor parts are removed to reveal the conic section.
• The conic section is highlighted in green color. It is a hyperbola.
♦ We see that, a hyperbola has two curves.
Degenerated conic sections
This can be explained in 4 steps:
1. Degenerated conic sections are special cases when the cutting plane passes through the vertex V.
2. We have seen that 𝛼 must be less than 90o. [step (2) below fig.11.4]
3. We have also seen that:
𝛽 can be equal to 90o [fig.11.4]
• In this situation, if the plane passes through the vertex, we can represent it as shown in fig.11.8(a) below:
 |
| Fig.11.8 |
• The section obtained will be a point.
4. We have also seen the cases where 𝛽 is less than 90o:
(i) 𝛽 can be less than 90o and greater than 𝛼 [fig.11.5]
• In this situation, if the plane passes through the vertex, we can represent it as shown in fig.11.8(b) above.
• The section obtained will be a point.
(ii) 𝛽 can be less than 90o and equal to 𝛼 [fig.11.6]
• In this situation, if the plane passes through the vertex, we can represent it as shown in fig.11.8(c) above.
• The plane just touches the lateral surface of the nappes. It does not make a cut.
• The section obtained will be a straight line.
• It is the degenerated case of a parabola.
(iii) 𝛽 can be less than 90o and less than 𝛼 [fig.11.7]
• In this situation, if the plane passes through the vertex, we can represent it as shown in fig.11.9(a) below:
 |
| Fig.11.9 |
• In fig.11.9(a) above, 𝛽 is less than 𝛼.
♦ So the plane is able to cut both upper nappe and lower nappe.
• In fig.(b), we can clearly see the major and minor parts.
• In fig.(c), the plane and the minor parts are removed to reveal the conic section.
• The conic section is highlighted in green color. It is a pair of two intersecting straight lines.
• It is the degenerated case of a hyperbola.
(iv) 𝛽 can be zero (which is less than 90o) and less than 𝛼
• In this situation, if the plane passes through the vertex, we can represent it as shown in fig.11.10(a) below:
 |
| Fig.11.10 |
• In fig.11.10(a) above, 𝛽 is zero. The axis lies in the plane.
♦ The plane is able to cut both upper nappe and lower nappe.
• In fig.(b), we can clearly see the two parts. They cannot be called as major and minor parts. Because, both are of the same size.
• In fig.(c), the plane and one of the parts are removed to reveal the conic section.
• The conic section is highlighted in green color. It is a pair of two intersecting straight lines.
• It is the degenerated case of a hyperbola.
So we have seen circle, ellipse, parabola and hyperbola. In the next section, we will see more details about circles.
No comments:
Post a Comment