In the previous section, we saw the basics of the rectangular coordinate system. In this section, we will see how this system can be used to fix the position of any object in space.
• In fig.12.4 below, P is a point in space.
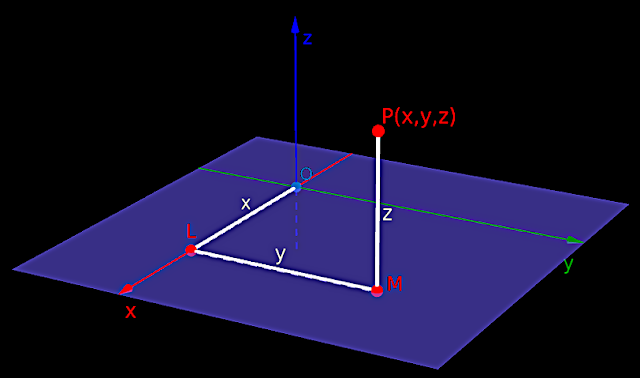 |
| Fig.12.4 |
• We want to write the position of P. It can be done in 6 steps:
1. The first step always is to drop a perpendicular from the given point, onto the XY-plane.
• In the above fig.12.4, the foot of the perpendicular is marked as M.
♦ We must measure the length of PM.
• PM is parallel to the z-axis. So the length of PM is denoted as ‘z’.
• ‘z’ should be given the proper sign.
♦ If PM is above the XY-plane, then z is +ve.
♦ If PM is below the XY-plane, then z is -ve.
2. The second step always is to drop a perpendicular from M onto the x-axis.
• In the above fig.12.4, the foot of the perpendicular is marked as L.
♦ We must measure the length of ML.
• ML is parallel to the y-axis. So the length of ML is denoted as ‘y’.
• ‘y’ should be given the proper sign.
♦ If ML is on the +ve side of the y-axis, then y is +ve.
♦ If ML is on the -ve side of the y-axis, then y is -ve.
3. The third step always is to measure OL.
• OL is on the x-axis. So the length of OL is denoted as ‘x’.
• ‘x’ should be given the proper sign.
♦ If OL is on the +ve side of the x-axis, then x is +ve.
♦ If OL is on the -ve side of the x-axis, then x is -ve.
4. The fourth and final step always is to write x, y and z together as an ordered triplet: (x,y,z)
• To specify the position of point P, we write: P(x,y,z)
5. Since x, y and z are given the proper signs, anybody can get an idea about the octant in which P is situated.
6. Anybody can get an idea about the distances also.
♦ The magnitude of x is the distance of P from the YZ-Plane.
♦ The magnitude of y is the distance of P from the XZ-Plane.
♦ The magnitude of z is the distance of P from the XY-Plane.
Let us see two examples.
Example 1:
This can be written in 6 steps:
1. In fig.12.5 below, P is a point in space. Let us assume that, it's position is not known. Our task is to find it's position with reference to the three axes.
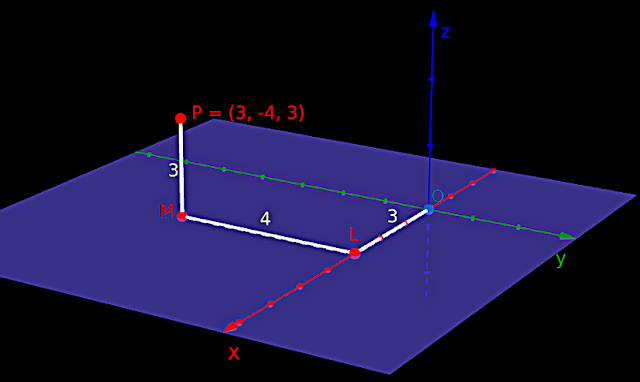 |
| Fig.12.5 |
2. First we drop the perpendicular PM onto the XY-plane. Then we measure the length of PM. In our present case, the length is 3 units.
•
PM is parallel to the z-axis.
•
PM is above the XY-plane.
♦ So z is +ve. We can write: z = 3
3. Next we drop the perpendicular ML onto the x-axis. Then we measure the length of ML. In our present case, the length is 4 units.
•
ML is parallel to the y-axis.
•
ML is on the -ve side of the y-axis.
♦ So y is -ve. We can write: y = -4
4. Finally, we measure the length of OL. In our present case, the length is 3 units.
•
OL lies on the x-axis.
•
OL is on the +ve side of the x-axis.
♦ So x is +ve. We can write: x = 3
5. So we obtained the values of x, y and z.
•
We write it as an ordered triplet: (3, -4, 3)
•
Thus the coordinates of P are written as: P(3, -4,3)
6. Using the sign of each coordinate, we can write the name of the octant. It can be done in 5 steps:
(i) z is +ve. So we get Z. It is one of the first four octants.
(ii) x is +ve and y is -ve. So we get XOY’
(iii) Thus the name of the octant is XOY’Z
(iv) The first three letters are XOY’.
•
Comparing this with the name of the quadrants of two-dimensional problems, we see that, XOY’ is the name of the fourth quadrant.
(v) So we can write:
The given point P is in the octant IV.
Example 2:
This can be written in 6 steps:
1. In fig.12.6 below, P is a point in space. Let us assume that, it's position is not
known. Our task is to find it's position with reference to the three
axes.
 |
| Fig.12.6 |
2. First we drop the perpendicular PM onto the XY-plane. Then we measure
the length of PM. In our present case, the length is 5 units.
•
PM is parallel to the z-axis.
•
PM is below the XY-plane.
♦ So z is -ve. We can write: z = -5
3.
Next we drop the perpendicular ML onto the x-axis. Then we measure the
length of ML. In our present case, the length is 3 units.
•
ML is parallel to the y-axis.
•
ML is on the +ve side of the y-axis.
♦ So y is +ve. We can write: y = 3
4. Finally, we measure the length of OL. In our present case, the length is 4 units.
•
OL lies on the x-axis.
•
OL is on the -ve side of the x-axis.
♦ So x is -ve. We can write: x = -4
5. So we obtained the values of x, y and z.
•
We write it as an ordered triplet: (-4, 3, -5)
•
Thus the coordinates of P are written as: P(-4, 3, -5)
6. Using the sign of each coordinate, we can write the name of the octant. It can be done in 5 steps:
(i) z is -ve. So we get Z'. It is one of the last four octants.
(ii) x is -ve and y is +ve. So we get X’OY
(iii) Thus the name of the octant is X’OYZ'
(iv) The first three letters are X’OY.
•
Comparing this with the name of the quadrants of two-dimensional problems, we see that, X’OY is the name of the second quadrant.
♦ The octant below second octant is (2+4) = 6
(v) So we can write:
The given point P is in the octant VI.
• So far in this section, we have been discussing this:
Given a point in space. How to find the coordinates of that point?
• We must be able to do the reverse also:
Given the coordinates of a point in space. How will we mark that point in space?
• This is similar to the task of the electrician that we saw in the previous section. He knows the measurements. His task is to use those measurements and hang the lamp at the correct position.
•
Consider fig.12.4 that we saw at the beginning of this section. For convenience, it is shown again below:
 |
| Fig.12.4 |
•
We are given the coordinates (x,y,z) of point P. We want to mark that point P in space. It can be done in 3 steps:
1. The first step always is to start from O and move along the x-axis.
♦ If the given ‘x’ is +ve, we must move in the +ve x direction.
♦ If the given ‘x’ is -ve, we must move in the -ve x direction.
•
Mark a point L in such a way that, OL = x units.
2. The second step always is to draw a line LM perpendicular to the x-axis.
♦ If the given ‘y’ is +ve, we must draw LM towards +ve y direction.
♦ If the given ‘y’ is -ve, we must draw LM towards -ve y direction.
•
The length of LM should be y units.
•
Also, LM must lie on the XY-plane.
3. The third step always is to draw a line MP perpendicular to the XY-plane.
♦ If the given ‘z’ is +ve, we must draw MP upwards from the XY-plane.
♦ If the given ‘z’ is -ve, we must draw MP downwards from the XY-plane.
•
The length of MP must be z units.
•
The end P of the line MP is the required point.
Let us see two examples.
Example 1:
This can be written in 4 steps:
1. Consider the fig.12.5 that we saw earlier. For convenience, it is shown again below:
 |
| Fig.12.5 |
•
Coordinates of P are given: (3,-4,3)
•
Our task is to mark the position of P in space.
2. First we start from O and move along the x-axis.
•
Since the given x is +ve, we move along the +ve direction of x-axis.
•
We mark the point L in such a way that, length of OL is 3 units.
3. Next we draw LM, perpendicular to the x-axis.
•
Since the given y is -ve, we must draw LM towards the -ve y direction.
•
Length of LM must be 4 units.
•
Also, LM must lie on the XY-plane.
4. Finally we draw MP, perpendicular to the XY-plane.
•
Since the given z is +ve, we must draw MP upwards from the XY-plane.
•
Length of MP must be 3 units.
•
The end P of the line MP is the required position.
Example 2:
This can be written in 4 steps:
1. Consider the fig.12.6 that we saw earlier. For convenience, it is shown again below:
 |
| Fig.12.6 |
•
Coordinates of P are given: (-4,3,-5)
•
Our task is to mark the position of P in space.
2. First we start from O and move along the x-axis.
•
Since the given x is -ve, we move along the -ve direction of x-axis.
•
We mark the point L in such a way that, length of OL is 4 units.
3. Next we draw LM, perpendicular to the x-axis.
•
Since the given y is +ve, we must draw LM towards the +ve y direction.
•
Length of LM must be 3 units.
•
Also, LM must lie on the XY-plane.
4. Finally we draw MP, perpendicular to the XY-plane.
•
Since the given z is -ve, we must draw MP downwards from the XY-plane.
•
Length of MP must be 5 units.
•
The end P of the line MP is the required position.
•
In this section, we accomplished two tasks:
Task 1:
To find the coordinates of a point with reference to x, y and z-axes.
Task 2: To mark a point in space when the coordinates of that point are given.
(Task 2 is the converse of task 1)
•
The same two tasks can be accomplished using another method. We will see it in the next section.
No comments:
Post a Comment