In the previous section, we completed a discussion on distance formula. In this section, we will see section formula.
• In our earlier classes, we have seen the application of section formula in two-dimensional problems.
• Let us recall the important points related to the section formula. It can be written in 2 steps:
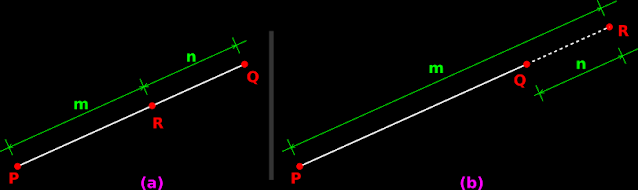
1. In fig.12.13 (a) below, the line segment PQ lies in the XY-plane.
♦ Point R lies between P and Q.
♦ Point R divides the segment PQ internally in the ratio m:n
♦ Coordinates of P and Q are (x1,y1) and (x2,y2) respectively.
• Then the coordinates of R will be: $\left(\frac{m x_2 + n x_1}{m+n}, \frac{m y_2 + n y_1}{m+n} \right)$.
 |
| Fig.12.13 |
2. In fig.12.13 (b) above, the line segment PQ lies in the XY-plane.
♦ Point R does not lie between P and Q. It is on the extension of the line PQ.
♦ Point R divides the segment PQ externally in the ratio m:n
♦ Coordinates of P and Q are (x1,y1) and (x2,y2) respectively.
• Then the coordinates of R will be:$\left(\frac{m x_2 - n x_1}{m-n}, \frac{m y_2 - n y_1}{m-n} \right)$.
• Now we will see the section formula when P(x1,y1,z1) and Q(x2,y2,z2) are two points in three-dimensional space.
♦ R (x,y,z) divides PQ in the ratio m:n.
♦ We need to derive expressions for x, y and z.
• First, we will derive an expression for z. It can be derived in 8 steps:
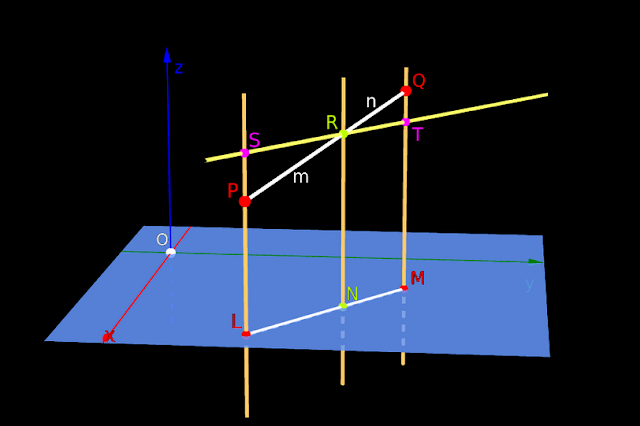
1. The first step is to drop perpendiculars from P, Q and R, on to the XY-plane.
• In fig.12.14 below, the XY-plane is shown in blue color.
♦ L is the foot of the perpendicular from P.
♦ M is the foot of the perpendicular from Q.
♦ N is the foot of the perpendicular from R.
 |
| Fig.12.14 |
2. Draw the line LM.
♦ Point N will lie on LM.
3. Through R, draw a line parallel to LM.
♦ Let this line meet PL (actually, it is the ‘extension of PL’) at S.
♦ Let this line meet QM at T.
4. The points P, Q, R, S and T are on the same plane. So we can show them separately as in fig.12.15 below:
 |
| Fig.12.15 |
• Consider the two triangles ΔPRS and ΔQRT.
• Let us analyze the angles of the two triangles. The analysis can be written in 5 steps:
(i) PS and QT are vertical lines because, they are drawn perpendicular to the XY-plane.
(ii) ST is a horizontal line because, it is drawn parallel to the XY-plane.
(iii) So we get: ∠PSR = ∠QTR = 90o
(iv) Angle at R is common to both triangles.
(v) So we have two angles same in both triangles. Consequently, the third angles (∠SPR and ∠TQR) will also be the same.
5. Since angles are the same in the two triangles, they are similar triangles.
• Since they are similar triangles, we can take ratio of sides:
(i) $\frac{\text{Side opposite ∠R in ΔPRS}}{\text{Side opposite ∠R in ΔQRT}}~=~\frac{\text{SP}}{\text{TQ}}$
(ii) $\frac{\text{Side opposite ∠PSR in ΔPRS}}{\text{Side opposite ∠QTR in ΔQRT}}~=~\frac{\text{PR}}{\text{QR}}~=~\frac{m}{n}$
(iii) $\frac{\text{Side opposite ∠SPR in ΔPRS}}{\text{Side opposite ∠TQR in ΔQRT}}~=~\frac{\text{SR}}{\text{TR}}$
6. For similar triangles, the three ratios will be equal. So we get:
$\frac{\text{SP}}{\text{TQ}}~=~\frac{m}{n}~=~\frac{\text{SR}}{\text{TR}}$
• We need only the first two ratios. We can write:
$\frac{m}{n}~=~\frac{\text{SP}}{\text{TQ}}$
7. Now we can write the lengths in terms of 'z'. It can be done in two steps:
(i) From fig.12.14, we get:
SP = SL – PL
• S is at the same level as R.
So SL = RN = z
• Also, PL = height of P = z1
• Therefore, SP = z-z1
(ii) Again from Fig.12.14, we get:
TQ = QM – TM
• T is at the same level as R
So TM = RN = z
• Also, QM = height of Q = z2
• Therefore, TQ = z2 – z
8. Substituting for SP and TQ in (6), we get:
$\begin{array}{ll}
{}&{\frac{m}{n}}
& {~=~}& {\frac{z - z_1}{z_2 - z}}
&{} \\
{\Rightarrow}&{m(z_2 - z)}
& {~=~}& {n(z - z_1)}
&{} \\
{\Rightarrow}&{m z_2 ~-~m z}
& {~=~}& {n z ~-~n z_1}
&{} \\
{\Rightarrow}&{m z_2 ~+~n z_1}
& {~=~}& {n z ~+~ m z}
&{} \\
{\Rightarrow}&{(m~+~n)z}
& {~=~}& {m z_2 ~+~n z_1}
&{} \\
{\Rightarrow}&{z}
& {~=~}& {\frac{m z_2 + n z_1}{m+n}}
&{} \\
\end{array}$
•
So we obtained the z-coordinate of R. We did this by dropping perpendiculars from P and Q, onto the XY-plane.
•
If we drop perpendiculars from P and Q, onto the XZ-plane, we will get the y-coordinate of R.
•
If we drop perpendiculars from P and Q, onto the YZ-plane, we will get the x-coordinate of R.
•
The perpendiculars onto the XZ-plane is shown in fig.12.16 below:
 |
| Fig.12.16 |
•
In the above fig.12.16, we see the two similar triangles ΔPRS and ΔQRT.
•
Based on the above fig., the reader may write all the steps for the y-coordinate in his/her own notebooks.
♦ The result will be: $y~=~\frac{m y_2 + n y_1}{m+n}$
•
Similarly, the reader may draw the diagrams and write the steps for x-coordinate also.
♦ The result will be: $x~=~\frac{m x_2 + n x_1}{m+n}$
So we can write a summary:
Case 1:
♦ P(x1,y1,z1) and Q(x2,y2,z2) are two points in space.
♦ Point R divides the line segment PQ internally in the ratio m:n
♦ Then the coordinates of R will be: $\left(\frac{m x_2 + n x_1}{m+n},~\frac{m y_2 + n y_1}{m+n},~\frac{m z_2 + n z_1}{m+n} \right)$
Case 2:
♦ P(x1,y1,z1) and Q(x2,y2,z2) are two points in space.
♦ Point R divides the line segment PQ externally in the ratio m:n
♦ Then the coordinates of R will be: $\left(\frac{m x_2 - n x_1}{m-n},~\frac{m y_2 - n y_1}{m-n},~\frac{m z_2 - n z_1}{m-n} \right)$
Case 3:
♦ Consider case 1.
♦ If R is the midpoint of PQ, then m:n will be 1:1
♦ So the coordinates of R will be: $\left(\frac{1 × x_2 + 1 × x_1}{1+1},~\frac{1 × y_2 + 1 × y_1}{1+1},~\frac{1 × z_2 + 1 × z_1}{1+1} \right)$
♦ That means: If R is the midpoint, then it's coordinates will be: $\left(\frac{x_2 + x_1}{2},~\frac{y_2 + y_1}{2},~\frac{z_2 + z_1}{2} \right)$
Case 4:
♦ Any ratio m:n can be written as k:1
♦ For that, we divide both m and n by n
♦ $\frac{m}{n}~=~\frac{m/n}{n/n}~=~\frac{m/n}{1}~=~\frac{k}{1}$
✰ So we get: $k~=~\frac{m}{n}$
♦ So the coordinates of R will be: $\left(\frac{k × x_2 + 1 ×
x_1}{k+1},~\frac{k × y_2 + 1 × y_1}{k+1},~\frac{k × z_2 + 1 ×
z_1}{k+1} \right)$
♦ That means, coordinates of R are: $\left(\frac{k x_2 + x_1}{1+k},~\frac{k y_2 + y_1}{1+k},~\frac{k z_2 + z_1}{1+k} \right)$
•
This case 4 is helpful in some special problems where, we need to calculate only one unknown value 'k' instead of two unknown values 'm' and 'n'.
Now we will see a solved example:
Solved example 12.7
Find the coordinates of point R which divides the line segment joining P(1,-2,3) and Q(3,4,-5) in the ratio 2:3 (i) internally, (ii) externally.
Solution:
Part (i): Dividing internally
1. The ratio m:n is 2:3
2. Coordinates of R will be: $\left(\frac{m x_2 + n x_1}{m+n},~\frac{m y_2 + n y_1}{m+n},~\frac{m z_2 + n z_1}{m+n} \right)$
3. Substituting the values, we get:
$\left(\frac{2 × 3 + 3 × 1}{2+3},~\frac{2 × 4 + 3 × -2}{2+3},~\frac{2 × -5 + 3 × 3}{2+3} \right)$
⇒ $\left(\frac{6 + 3}{5},~\frac{8 -6}{5},~\frac{-10 + 9}{5} \right)$
⇒ $\left(\frac{9}{5},~\frac{2}{5},~\frac{-1}{5} \right)$
Part (ii): Dividing externally
1. The ratio m:n is 2:3
2. Coordinates of R' will be: $\left(\frac{m x_2 - n x_1}{m-n},~\frac{m y_2 - n y_1}{m-n},~\frac{m z_2 - n z_1}{m-n} \right)$
3. Substituting the values, we get:
$\left(\frac{2 × 3 - 3 × 1}{2-3},~\frac{2 × 4 - 3 × -2}{2-3},~\frac{2 × -5 - 3 × 3}{2-3} \right)$
⇒ $\left(\frac{6 - 3}{-1},~\frac{8 +6}{-1},~\frac{-10 - 9}{-1} \right)$
⇒ $\left(\frac{3}{-1},~\frac{14}{-1},~\frac{-19}{-1} \right)$
⇒ (-3, -14, 19)
Check:
1. Fig.12.17 below shows the actual plot:
 |
| Fig.12.17 |
2. We have the coordinates of all four points:
P(1,-2,3), Q(3,4,-5), R(9/5, 2/5, -1/5) and R'(-3, -14, 19)
3. First we will check the internal division:
• Using the distance formula, we can find the lengths:
♦ PR = 37/9 units
♦ QR = 49/8 units
• Thus the ratio PR/QR = $\frac{37/9}{49/8}~=~\frac{2}{3}$
4. Next we will check the external division:
• Using the distance formula, we can find the lengths:
♦ PR' = 102/5 units
♦ QR' = 153/5 units
• Thus the ratio PR'/QR' = $\frac{102/5}{153/5}~=~\frac{2}{3}$
In the next section, we will see a few more solved examples.
No comments:
Post a Comment