In the previous section, we completed a discussion on conic sections. In this chapter, we will see three dimensional geometry.
The importance of three dimensional geometry can be explained using two simple examples.
Example 1:
This can be written in 5 steps:
1. Consider the point marked as ‘O’ in fig.12.1 below:
 |
| Fig.12.1 |
• Point 'O' is the bottom corner of a large room.
• Point 'O' is formed by the intersection of three items:
♦ The green wall.
♦ The red wall.
♦ The blue floor.
2. The green and red walls are adjacent walls. They are perpendicular to each other. Both walls are perpendicular to the floor.
• So we can write:
The walls and the floor are mutually perpendicular to each other.
3. The electrician wants to fix a lamp.
♦ The lamp must be on the green wall.
♦ The lamp must be 4 meters away from the red wall.
♦ The lamp must be at a height of 3 meters above the floor.
4. To fix the position of the lamp, the electrician adopts two steps:
(i) First he marks point A
• This point is at a distance of 4 meters from O
• The distance 4 meters is measured along a line perpendicular to red wall.
(ii) Then he marks point B
• This point is at a distance of 3 meters from A.
• The distance 3 m is measured along a line perpendicular to the floor.
5. We can write:
• To fix the position of the lamp, the electrician requires the two numbers: ‘4’ and ‘3’.
• He also requires two adjacent perpendicular planes: ‘red wall’ and ‘blue floor’.
6. We are already familiar with this type of problems. The numbers ‘3’ and ‘4’ are the coordinates. They are written as an ordered pair (4,3).
• When viewed from the side of the room, the floor will appear as a line. It is the x-axis.
• When viewed from the side of the room, the red wall will appear as a line. It is the y-axis.
• When viewed from the side of the room, the green wall will appear as a plane. It is the xy-plane.
• So this is a two-dimensional problem. Every point in a two-dimensional problem will lie in the xy-plane.
Example 2:
This can be written in steps:
1. Fig.12.2 below shows the same room that we saw in example 1.
 |
| Fig.12.2 |
2. The electrician wants to fix a lamp.
♦ The lamp must hang from the ceiling.
♦ The lamp must be 4 meters away from the red wall.
♦ The lamp must be 5 meters away from the green wall.
♦ The lamp must be at a height of 3 meters above the floor.
3. To fix the position of the lamp, the electrician adopts three steps:
(i) First he marks point A.
•
This point is at a distance of 4 meters from O.
•
The distance 4 meters is measured along a line perpendicular to red wall.
(ii) Then he marks point B.
•
This point is at a distance of 5 meters from A.
•
The distance 5 m is measured along a line perpendicular to the green wall.
(iii) Then he marks point C.
•
This point is at a distance of 3 meters from B.
•
The distance 3 m is measured along a line perpendicular to the
floor.
4. We can write:
To fix the position of the lamp, the electrician requires the three numbers '4', ‘5’ and ‘3’. He also requires three adjacent perpendicular planes ‘red wall’, ‘green wall’ and ‘blue floor’
5. This is a new type of problem for us. The numbers ‘4’, ‘5’ and ‘3’ are the coordinates. They are written as an ordered triplet (4, 5, 3).
•
This is a three-dimensional problem.
Let us compare the two examples. The comparison can be written in 2 steps:
1. In the example 1, two coordinates and two adjacent perpendicular planes are sufficient to fix the position of an object.
•
The two numbers are called coordinates of the object with reference to the two perpendicular planes.
•
The object will lie on a third plane which is perpendicular to the first two planes.
•
It is a two-dimensional problem. Since we have enough practice in two-dimensional problems, we can ignore the planes and use just the x and y axes.
2. In the example 2, three coordinates and three adjacent perpendicular planes are required to fix the position of an object.
•
The three numbers are called coordinates of the object with reference to the three perpendicular planes.
•
The object will not be on any of the three planes. We say that, the object is situated in ‘space’.
•
It is a three-dimensional problem.
In many scientific and engineering problems, we will need three coordinates to describe the position of an object. So we must develop a three-dimensional mathematical model which can be easily set up for any given problem. Such a model can be described in 10 steps:
1. Fig.12.3 below shows three mutually perpendicular planes.
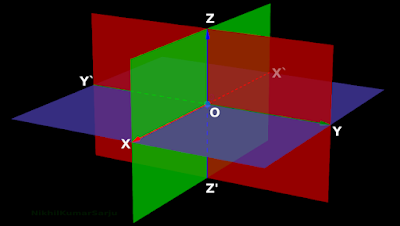 |
| Fig.12.3 |
♦ One plane is red in color.
♦ Another plane is green in color.
♦ The third plane is blue in color.
2. Intersection of the three planes gives us three different lines:
♦ Intersection of green and blue planes give us the line X`OX.
✰ This line is shown in red color.
♦ Intersection of red and blue planes give us the line Y`OY.
✰ This line is shown in green color.
♦ Intersection of red and green planes give us the line Z`OZ.
✰ This line is shown in blue color.
•
The three lines obtained in this way are mutually perpendicular to each other. The three lines intersect at O.
3. Now we have two items:
(i) The planes mentioned in step (1)
(ii) The lines mentioned in step (2)
•
These two items together gives us a simple but powerful system to fix the position of any point in space.
•
This system is known as the rectangular coordinate system.
•
We will soon see how this system can be used to fix points in space.
4. Before that, we will give specific names to each of the different components of the system.
(i) Naming the lines:
♦ Line X’OX is called x-axis.
♦ Line Y’OY is called y-axis.
♦ Line Z’OZ is called z-axis.
(ii) Naming the planes:
•
Two axes lie on the blue plane: x-axis and y-axis.
♦ This plane is called XY-plane.
♦ z-axis is perpendicular to the XY-plane.
•
Two axes lie on the green plane: x-axis and z-axis.
♦ This plane is called XZ-plane.
♦ y-axis is perpendicular to the XZ-plane.
•
Two axes lie on the red plane: y-axis and z-axis.
♦ This plane is called YZ-plane.
♦ x-axis is perpendicular to the YZ-plane.
(iii) The point O is called origin.
5. The blue plane (XY-plane) is considered to be horizontal.
•
So Z’OZ (z-axis) will be vertical.
6. XY-plane is considered to be the plane of the paper.
7. Positive and negative distances:
This can be explained in 3 steps.
(i) The XY-plane divides z-axis into two parts: OZ and OZ’.
•
Consider the distances measured along the z-axis.
♦ Distances measured from O towards Z are taken as +ve.
♦ Distances measured from O towards Z’ are taken as -ve.
(ii) The XZ-plane divides y-axis into two parts: OY and OY’.
•
Consider the distances measured along the y-axis.
♦ Distances measured from O towards Y are taken as +ve.
♦ Distances measured from O towards Y’ are taken as -ve.
(iii) The YZ-plane divides x-axis into two parts: OX and OX’.
•
Consider the distances measured along the x-axis.
♦ Distances measured from O towards X are taken as +ve.
♦ Distances measured from O towards X’ are taken as -ve.
8. Naming of octants.
This can be written in 2 steps:
(i) We know that, the XY-plane is horizontal.
•
We have a space above this horizontal plane.
♦ YZ-plane and XZ-plane together, divides this space into four compartments.
♦ Each of these compartments is called an octant.
•
The octant formed by +ve x and +ve y axes is called octant I.
♦ It can be named as XOYZ.
✰ In two-dimensional problems, +ve x and +ve y axes give quadrant I.
✰ It is named XOY.
•
The octant formed by -ve x and +ve y axes is called octant II.
♦ It can be named as X'OYZ.
✰ In two-dimensional problems, -ve x and +ve y axes give quadrant II.
✰ It is named X'OY.
•
The octant formed by -ve x and -ve y axes is called octant III.
♦ It can be named as X'OY'Z.
✰ In two-dimensional problems, -ve x and -ve y axes give quadrant III.
✰ It is named X'OY'.
•
The octant formed by +ve x and -ve y axes is called octant IV.
♦ It can be named as XOY`Z.
✰ In two-dimensional problems, +ve x and -ve y axes give quadrant IV.
✰ It is named XOY'.
(ii) We know that, the XY-plane is horizontal.
•
We have a space below this horizontal plane.
♦ YZ-plane and XZ-plane together, divides this space into four compartments.
♦ Each of these compartments is called an octant.
•
The octant formed by +ve x and +ve y axes is called octant V.
♦ It can be named as XOYZ'.
•
The octant formed by -ve x and +ve y axes is called octant VI.
♦ It can be named as X`OYZ'.
•
The octant formed by -ve x and -ve y axes is called octant VII.
♦ It can be named as X`OY`Z'.
•
The octant formed by +ve x and -ve y axes is called octant VIII.
♦ It can be named as XOY`Z'.
9. We see a pattern in the names of the octants. It can be explained in 5 steps:
(i) Consider octant I. Adding four, we get octant V.
•
Both have the same name except the ‘Z’ part.
♦ Name of octant I is XOYZ.
♦ Name of octant V is XOYZ’.
✰ Obviously, V is directly below I.
(ii) Consider octant II. Adding four, we get octant VI.
•
Both have the same name except the ‘Z’ part.
♦ Name of octant II is X'OYZ.
♦ Name of octant V is X'OYZ’.
✰ Obviously, VI is directly below II.
(iii) Consider octant III. Adding four, we get octant VII.
•
Both have the same name except the ‘Z’ part.
♦ Name of octant III is X'OY'Z.
♦ Name of octant VII is X'OY'Z’.
✰ Obviously, VII is directly below III.
(iv) Consider octant IV. Adding four, we get octant VIII.
•
Both have the same name except the ‘Z’ part.
♦ Name of octant IV is XOY'Z.
♦ Name of octant VIII is XOY'Z’.
✰ Obviously, VIII is directly below IV.
(v) So, if we can remember the details about the first four octants, we can easily write the details about the remaining four octants.
•
The good news is that, there is not much to remember about the first four octants.
•
This is because:
♦ the names of the first four octants
♦ is similar to
♦ the names of the four quadrants in two-dimensional problems.
•
This is shown below:
♦ Quadrant I is XOY; Octant I is XOYZ
♦ Quadrant II is X'OY; Octant II is X'OYZ
♦ Quadrant III is X'OY'; Octant III is X'OY'Z
♦ Quadrant IV is XOY'; Octant IV is XOY'Z
◼ So the bottom line is this:
♦ Since we are familiar with the quadrants of two-dimensional problems,
♦ we can easily write the details about
♦ the eight octants of three-dimensional problems.
•
This will become clear when we do actual problems.
10. A comparison between quadrants and octants can be written in 2 steps:
(i) In two-dimensional problems, the x-axis and y-axis together, divides an area into four quadrants. Recall that, 'quad' indicates four.
(ii) In three-dimensional problems, the XY-plane, XZ-plane and YZ-plane together, divides a space into eight octants. Recall that, 'oct' indicates eight.
Now we know the basic details about the rectangular coordinate system. In the next section, we will see how this system can be used to fix the position of any object in space.
No comments:
Post a Comment