In the previous section, we completed a discussion on the basics of the rectangular coordinate system. In this section, we will see distance between two points.
•
Consider a two-dimensional problem in which two points P(x1,y1) and Q(x2,y2) lie on the XY-plane.
♦ We know that, the distance PQ will be $\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2}$.
•
Now we will derive a formula to find the distance between two points P(x1,y1,z1) and Q(x2,y2,z2) which lie in space.
•
It can be derived in 10 steps:
1. In fig.12.11(a) below, P(x1,y1,z1) and Q(x2,y2,z2) are two points in space.
•
To derive the formula, we need a rectangular prism in which PQ is a diagonal.
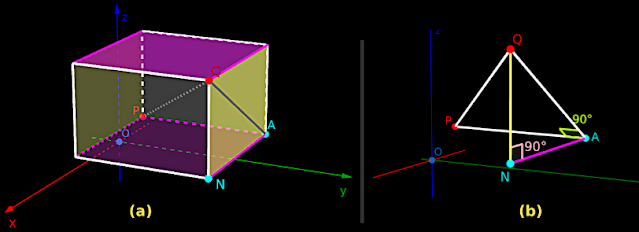 |
| Fig.12.11 |
2. The rectangular prism can be obtained in 5 steps:
(i) Draw two magenta planes.
♦ Those two planes must be parallel to the XY-plane.
✰ One plane must pass through P.
✰ The other plane must pass through Q.
(ii) Draw two yellow planes.
♦ Those two planes must be parallel to the XZ-plane.
✰ One plane must pass through P.
✰ The other plane must pass through Q.
(iii) Draw two gray planes.
♦ Those two planes must be parallel to the YZ-plane.
✰ One plane must pass through P.
✰ The other plane must pass through Q.
(iv) We have drawn six planes.
•
The six planes together enclose a three-dimensional-shape.
♦ The planes were drawn parallel to the coordinate planes.
♦ So all interior angles of the three-dimensional-shape are 90o
♦ So the three-dimensional-shape is a rectangular prism.
•
Also note that, PQ is a diagonal of this rectangular prism.
3. We want four points from the rectangular prism.
♦ They are: P, Q, A and N
•
Remember that, our task is to find the distance PQ.
4. Let us obtain a right angled triangle inside the prism. It can be obtained in 5 steps:
(i) Consider the magenta plane in which PA lies.
(ii) Also consider the yellow plane in which AQ lies.
(iii) The magenta plane is perpendicular to the yellow plane.
♦ So PA is perpendicular to AQ.
(iv) Thus the angle between PA and AQ is 90o. This is shown in fig.b
(v) We can write:
PAQ is a right angled triangle. It is right angled at A
•
So we get: PQ2 = PA2 + AQ2
5. Let us obtain one more right angled triangle inside the prism. It can be obtained in 5 steps:
(i) Consider the magenta plane in which AN lies.
(ii) Also consider the yellow plane in which NQ lies.
(iii) The magenta plane is perpendicular to the yellow plane.
♦ So AN is perpendicular to NQ
(iv) Thus the angle between AN and NQ is 90o. This is shown in fig.b
(v) We can write:
ANQ is a right angled triangle. It is right angled at N.
•
So we get: AQ2 = AN2 + NQ2
6. Now we can substitute for AQ in (4). We get:
PQ2 = PA2 + AN2 + NQ2
•
So to find PQ, we need PA, AN and NQ
7. First we will find PA. It can be done in 4 steps:
(i) Consider the line PA
♦ PA lies on the yellow plane, which is parallel to the YZ-plane.
♦ All points on that yellow plane will have the same x-coordinate.
♦ So P and A will have the same x-coordinate.
(ii) PA lies on the magenta plane, which is parallel to the XY-plane.
♦ All points on that magenta plane will have the same z-coordinate.
♦ So P and A will have the same z-coordinate.
(iii) We need to pay special attention to the y-coordinates of P and A. They will be different.
♦ We already know the y-coordinate of P. It is: y1
•
Point A lies on the yellow plane passing through Q.
♦ So the y-coordinates of A and Q will be the same, which is y2
(iv) So the distance PA = y2 – y1
8. Using a similar analysis as in (7), we will get:
♦ AN = x2 – x1
♦ NQ = z2 - z1
9. Now we have the lengths PA, AN and NQ
•
Substituting those lengths in (6), we get:
PQ2 = (y2 – y1)2 + (x2 – x1)2 + (z2 – z1)2
•
So the distance formula is: $\rm{PQ}~=~\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}$
10. Suppose that, point P is the origin O
•
Then we can write: x1 = 0, y1 = 0 and z1 = 0
•
So the distance formula becomes:
$\rm{OQ}~=~\sqrt{x_2^2~+~y_2^2~+~z_2^2}$
♦ This formula gives the distance of any point Q from the origin.
Now we will see some solved examples.
Solved example 12.3
Find the distance between the points P(1, –3, 4) and Q (– 4, 1, 2).
Solution:
1. We have the distance formula:
$\rm{PQ}~=~\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}$
2. So we get:
$\begin{array}{ll}
{}&{\rm{PQ}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(-4 - 1)^2~+~(1 -~-3)^2~+~(2 - 4)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(-5)^2~+~(4)^2~+~(-2)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{25~+~16~+~4}}
&{} \\
{}&{}
&
{~=~}& {\sqrt{45}}
&{} \\
{}&{}
&
{~=~}& {3\sqrt{5}~\rm{units}}
&{} \\
\end{array}$
Solved example 12.4
Show that the points P (–2, 3, 5), Q (1, 2, 3) and R (7, 0, –1) are collinear.
Solution:
1. We are given three points P, Q and R
•
Using those three points, we can draw three line segments:
PQ, QR and PR
•
Let us find the lengths of those three line segments.
2. First we will find PQ
$\begin{array}{ll}
{}&{\rm{PQ}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(1 -~-2)^2~+~(2 - 3)^2~+~(3 - 5)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(3)^2~+~(-1)^2~+~(-2)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{9~+~1~+~4}}
&{} \\
{}&{}
& {~=~}& {\sqrt{14}~\rm{units}}
&{} \\
\end{array}$
3. Next, we will find QR
$\begin{array}{ll}
{}&{\rm{QR}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(7 - 1)^2~+~(0 - 2)^2~+~(-1 - 3)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(6)^2~+~(-2)^2~+~(-4)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{36~+~4~+~16}}
&{} \\
{}&{}
&
{~=~}& {\sqrt{56}}
&{} \\
{}&{}
&
{~=~}& {2\sqrt{14}~\rm{units}}
&{} \\
\end{array}$
4. Finally, we will find PR
$\begin{array}{ll}
{}&{\rm{PR}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(7 - ~-2)^2~+~(0 - 3)^2~+~(-1 - 5)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(9)^2~+~(-3)^2~+~(-6)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{81~+~9~+~36}}
&{} \\
{}&{}
&
{~=~}& {\sqrt{136}}
&{} \\
{}&{}
&
{~=~}& {3\sqrt{14}~\rm{units}}
&{} \\
\end{array}$
5. We see that: PQ + QR = (√14 + 2√14) = 3√14 = PR
•
In the fig.12.12 below, PR is the shortest distance from P to R.
 |
| Fig.12.12 |
•
If we move from P to R through Q, then the distance will be greater.
•
It follows that:
If Q is not in line with P and R. the sum (PQ + QR) will be greater than PR.
•
But we saw that, the sum is equal to PR.
•
So we can write: P, Q and R are collinear.
6. In the above fig.12.12, it is clear that, (PQ' + Q'R) cannot be less than PR.
•
That means, there are only two possibilities:
♦ The sum is equal to PR.
♦ The sum is greater than PR.
7. Based on the above step (6), we can write the general steps to check whether three points are collinear:
(i) We are given three points P, Q and R.
(ii) Find the lengths PQ, QR and PR.
(iii) Pick out the longest length.
(iv) Add the remaining two lengths.
(v) If the sum is equal to the longest length, then the three points are collinear.
(vi) If the sum is greater than the longest length, then the three points are not collinear.
Solved example 12.5
Are the points A (3, 6, 9), B (10, 20, 30) and C (25, – 41, 5), the vertices
of a right angled triangle?
Solution:
1. We are given three points A, B and C
•
Using those three points, we can draw three line segments:
AB, BC and AC
•
Let us find the lengths of those three line segments.
2. First we will find AB
$\begin{array}{ll}
{}&{\rm{AB}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(10 -3)^2~+~(20 - 6)^2~+~(30 - 9)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(7)^2~+~(14)^2~+~(21)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{49~+~196~+~441}}
&{} \\
{}&{}
& {~=~}& {\sqrt{686}~\rm{units}}
&{} \\
\end{array}$
3. Next, we will find BC
$\begin{array}{ll}
{}&{\rm{BC}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(25 - 10)^2~+~(-41 - 20)^2~+~(5 - 30)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(15)^2~+~(-61)^2~+~(-25)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{225~+~3721~+~625}}
&{} \\
{}&{}
&
{~=~}& {\sqrt{4571}}
&{} \\
\end{array}$
4. Finally, we will find AC
$\begin{array}{ll}
{}&{\rm{AC}}
& {~=~}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2~+~(z_2 - z_1)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(25 - ~3)^2~+~(-41 - 6)^2~+~(5 - 9)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{(22)^2~+~(-47)^2~+~(-4)^2}}
&{} \\
{}&{}
& {~=~}& {\sqrt{484~+~2209~+~16}}
&{} \\
{}&{}
&
{~=~}& {\sqrt{2709}}
&{} \\
\end{array}$
5. Based on the above steps, we get:
AB2 = 686, BC2 = 4571 and AC2 =2709
6.Now we can check whether A, B and C are the vertices of a right angled triangle.
(i) In the above result, mark out the largest square, which is BC2
(ii) Add the remaining squares:
AB2 + AC2 = (686 + 2709) = 3395
(iii) We see that, AB2 + AC2≠ BC2
•
So the vertices do not form a right angled triangle.
Solved example 12.6
Find the equation of the set of points P such that PA2 + PB2 = 2k2, where A and B are points (3,4,5) and (-1,3,-7) respectively.
Solution:
1. Let the coordinates of P be (x,y,z)
2. Then PA2 = (x-3)2 + (y-4)2 + (z-5)^2
3. Also, PB2 = (x+1)2 + (y-3)2 + (z+7)^2
4. So we can write:
PA2 + PB2 = (x-3)2 + (y-4)2 + (z-5)^2 + (x+1)2 + (y-3)2 + (z+7)^2
= x2 - 6x + 9 + y2 -8y + 16 + z2 - 10z + 25
+ x2 +2x + 2 + y2 -6y + 9 + z2 + 14z + 49
= 2x2 -4x + 11 +2y2 -14y +25 +z2 +4z +64
= 2x2 + 2y2 + 2z2 -4x -14y +4z +100
5. So the given equation becomes:
2x2 + 2y2 + 2z2 - 4x - 14y + 4z + 100 = 2k2
⇒ x2 + y2 + z2 - 2x - 7y + 2z + 50 = k2
The link below gives a few more solved examples:
In the next section, we will see section formula.
No comments:
Post a Comment