Chapter 12 - Three Dimensional Geometry

In the previous section, we completed a discussion on conic sections. In this chapter, we will see three dimensional geometry.

The importance of three dimensional geometry can be explained using two simple examples.
Example 1:
This can be written in 5 steps:
1. Consider the point marked as ‘O’ in fig.12.1 below:

Fig.12.1

• Point 'O' is the bottom corner of a large room.
• Point 'O' is formed by the intersection of three items:
   ♦ The green wall.
   ♦ The red wall.
   ♦ The blue floor.
2. The green and red walls are adjacent walls. They are perpendicular to each other. Both walls are perpendicular to the floor.
• So we can write:
The walls and the floor are mutually perpendicular to each other.
3. The electrician wants to fix a lamp.
   ♦ The lamp must be on the green wall.
   ♦ The lamp must be 4 meters away from the red wall.
   ♦ The lamp must be at a height of 3 meters above the floor.
4. To fix the position of the lamp, the electrician adopts two steps:
(i) First he marks point A
• This point is at a distance of 4 meters from O
• The distance 4 meters is measured along a line perpendicular to red wall.
(ii) Then he marks point B
• This point is at a distance of 3 meters from A.
• The distance 3 m is measured along a line perpendicular to the floor.
5. We can write:
• To fix the position of the lamp, the electrician requires the two numbers: ‘4’ and ‘3’.
• He also requires two adjacent perpendicular planes: ‘red wall’ and ‘blue floor’.
6. We are already familiar with this type of problems. The numbers ‘3’ and ‘4’ are the coordinates. They are written as an ordered pair (4,3).
• When viewed from the side of the room, the floor will appear as a line. It is the x-axis.     
• When viewed from the side of the room, the red wall will appear as a line. It is the y-axis.
• When viewed from the side of the room, the green wall will appear as a plane. It is the xy-plane.
• So this is a two-dimensional problem. Every point in a two-dimensional problem will lie in the xy-plane.

Example 2:
This can be written in steps:
1. Fig.12.2 below shows the same room that we saw in example 1.

Fig.12.2

2. The electrician wants to fix a lamp.
   ♦ The lamp must hang from the ceiling.
   ♦ The lamp must be 4 meters away from the red wall.
   ♦ The lamp must be 5 meters away from the green wall.
   ♦ The lamp must be at a height of 3 meters above the floor.
3. To fix the position of the lamp, the electrician adopts three steps:
(i) First he marks point A.
• This point is at a distance of 4 meters from O.
• The distance 4 meters is measured along a line perpendicular to red wall.
(ii) Then he marks point B.
• This point is at a distance of 5 meters from A.
• The distance 5 m is measured along a line perpendicular to the green wall.
(iii) Then he marks point C.
• This point is at a distance of 3 meters from B.
• The distance 3 m is measured along a line perpendicular to the
floor.
4. We can write:
To fix the position of the lamp, the electrician requires the three numbers '4', ‘5’ and ‘3’. He also requires three adjacent perpendicular planes ‘red wall’, ‘green wall’ and ‘blue floor’
5. This is a new type of problem for us. The numbers ‘4’, ‘5’ and ‘3’ are the coordinates. They are written as an ordered triplet (4, 5, 3).
• This is a three-dimensional problem.

---

Let us compare the two examples. The comparison can be written in 2 steps:
1. In the example 1, two coordinates and two adjacent perpendicular planes are sufficient to fix the position of an object.
• The two numbers are called coordinates of the object with reference to the two perpendicular planes.
• The object will lie on a third plane which is perpendicular to the first two planes.
• It is a two-dimensional problem. Since we have enough practice in two-dimensional problems, we can ignore the planes and use just the x and y axes.
2. In the example 2, three coordinates and three adjacent perpendicular planes are required to fix the position of an object.
• The three numbers are called coordinates of the object with reference to the three perpendicular planes.
• The object will not be on any of the three planes. We say that, the object is situated in ‘space’.
• It is a three-dimensional problem.

---

In many scientific and engineering problems, we will need three coordinates to describe the position of an object. So we must develop a three-dimensional mathematical model which can be easily set up for any given problem. Such a model can be described in 10 steps:

1. Fig.12.3 below shows three mutually perpendicular planes.

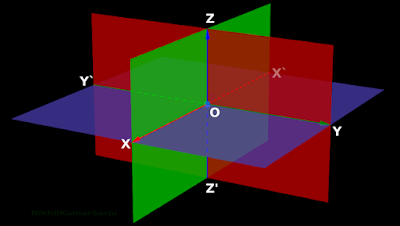Fig.12.3

   ♦ One plane is red in color.
   ♦ Another plane is green in color.
   ♦ The third plane is blue in color.
2. Intersection of the three planes gives us three different lines:
   ♦ Intersection of green and blue planes give us the line X`OX.
         ✰ This line is shown in red color.
   ♦ Intersection of red and blue planes give us the line Y`OY.
         ✰ This line is shown in green color.
   ♦ Intersection of red and green planes give us the line Z`OZ.
         ✰ This line is shown in blue color.
• The three lines obtained in this way are mutually perpendicular to each other. The three lines intersect at O.
3. Now we have two items:
(i) The planes mentioned in step (1)
(ii) The lines mentioned in step (2)  
• These two items together gives us a simple but powerful system to fix the position of any point in space.
• This system is known as the rectangular coordinate system.
• We will soon see how this system can be used to fix points in space.
4. Before that, we will give specific names to each of the different components of the system.
(i) Naming the lines:
   ♦ Line X’OX is called x-axis.
   ♦ Line Y’OY is called y-axis.
   ♦ Line Z’OZ is called z-axis.
(ii) Naming the planes:
• Two axes lie on the blue plane: x-axis and y-axis.
   ♦ This plane is called XY-plane.
   ♦ z-axis is perpendicular to the XY-plane.
• Two axes lie on the green plane: x-axis and z-axis.
   ♦ This plane is called XZ-plane.
   ♦ y-axis is perpendicular to the XZ-plane.
• Two axes lie on the red plane: y-axis and z-axis.
   ♦ This plane is called YZ-plane.
   ♦ x-axis is perpendicular to the YZ-plane.
(iii) The point O is called origin.
5. The blue plane (XY-plane) is considered to be horizontal.
• So Z’OZ (z-axis) will be vertical.
6. XY-plane is considered to be the plane of the paper.
7. Positive and negative distances:
This can be explained in 3 steps.
(i) The XY-plane divides z-axis into two parts: OZ and OZ’.
• Consider the distances measured along the z-axis.
   ♦ Distances measured from O towards Z are taken as +ve.
   ♦ Distances measured from O towards Z’ are taken as -ve.
(ii) The XZ-plane divides y-axis into two parts: OY and OY’.
• Consider the distances measured along the y-axis.
   ♦ Distances measured from O towards Y are taken as +ve.
   ♦ Distances measured from O towards Y’ are taken as -ve.
(iii) The YZ-plane divides x-axis into two parts: OX and OX’.
• Consider the distances measured along the x-axis.
   ♦ Distances measured from O towards X are taken as +ve.
   ♦ Distances measured from O towards X’ are taken as -ve.
8. Naming of octants.
This can be written in 2 steps:
(i) We know that, the XY-plane is horizontal.
• We have a space above this horizontal plane.
   ♦ YZ-plane and XZ-plane together, divides this space into four compartments.
   ♦ Each of these compartments is called an octant.
• The octant formed by +ve x and +ve y axes is called octant I.
   ♦ It can be named as XOYZ.
         ✰ In two-dimensional problems, +ve x and +ve y axes give quadrant I.
         ✰ It is named XOY.
• The octant formed by -ve x and +ve y axes is called octant II.
   ♦ It can be named as X'OYZ.
         ✰ In two-dimensional problems, -ve x and +ve y axes give quadrant II.
         ✰ It is named X'OY.
• The octant formed by -ve x and -ve y axes is called octant III.
   ♦ It can be named as X'OY'Z.
         ✰ In two-dimensional problems, -ve x and -ve y axes give quadrant III.
         ✰ It is named X'OY'.
• The octant formed by +ve x and -ve y axes is called octant IV.
   ♦ It can be named as XOY`Z.
         ✰ In two-dimensional problems, +ve x and -ve y axes give quadrant IV.
         ✰ It is named XOY'.
(ii) We know that, the XY-plane is horizontal.
• We have a space below this horizontal plane.
   ♦ YZ-plane and XZ-plane together, divides this space into four compartments.
   ♦ Each of these compartments is called an octant.
• The octant formed by +ve x and +ve y axes is called octant V.
   ♦ It can be named as XOYZ'.
• The octant formed by -ve x and +ve y axes is called octant VI.
   ♦ It can be named as X`OYZ'.
• The octant formed by -ve x and -ve y axes is called octant VII.
   ♦ It can be named as X`OY`Z'.
• The octant formed by +ve x and -ve y axes is called octant VIII.
   ♦ It can be named as XOY`Z'.
9. We see a pattern in the names of the octants. It can be explained in 5 steps:
(i) Consider octant I. Adding four, we get octant V.
• Both have the same name except the ‘Z’ part.
   ♦ Name of octant I is XOYZ.
   ♦ Name of octant V is XOYZ’.
         ✰ Obviously, V is directly below I.
(ii) Consider octant II. Adding four, we get octant VI.
• Both have the same name except the ‘Z’ part.
   ♦ Name of octant II is X'OYZ.
   ♦ Name of octant V is X'OYZ’.
         ✰ Obviously, VI is directly below II.
(iii) Consider octant III. Adding four, we get octant VII.
• Both have the same name except the ‘Z’ part.
   ♦ Name of octant III is X'OY'Z.
   ♦ Name of octant VII is X'OY'Z’.
         ✰ Obviously, VII is directly below III.
(iv) Consider octant IV. Adding four, we get octant VIII.
• Both have the same name except the ‘Z’ part.
   ♦ Name of octant IV is XOY'Z.
   ♦ Name of octant VIII is XOY'Z’.
         ✰ Obviously, VIII is directly below IV.
(v) So, if we can remember the details about the first four octants, we can easily write the details about the remaining four octants.
• The good news is that, there is not much to remember about the first four octants.
• This is because:
   ♦ the names of the first four octants
   ♦ is similar to
   ♦ the names of the four quadrants in two-dimensional problems.
• This is shown below:
   ♦ Quadrant I is XOY;       Octant I is XOYZ
   ♦ Quadrant II is X'OY;     Octant II is X'OYZ
   ♦ Quadrant III is X'OY';   Octant III is X'OY'Z
   ♦ Quadrant IV is XOY';    Octant IV is XOY'Z
◼ So the bottom line is this:
   ♦ Since we are familiar with the quadrants of two-dimensional problems,
   ♦ we can easily write the details about
   ♦ the eight octants of three-dimensional problems.
• This will become clear when we do actual problems.
10. A comparison between quadrants and octants can be written in 2 steps:
(i) In two-dimensional problems, the x-axis and y-axis together, divides an area into four quadrants. Recall that, 'quad' indicates four.
(ii) In three-dimensional problems, the XY-plane, XZ-plane and YZ-plane together, divides a space into eight octants. Recall that, 'oct' indicates eight.

---

Now we know the basic details about the rectangular coordinate system. In the next section, we will see how this system can be used to fix the position of any object in space.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 11.14 - Miscellaneous Examples

In the previous section, we completed a discussion on hyperbola. In this section, we will see some miscellaneous examples.

Solved example 11.18
The focus of the parabolic mirror shown in fig.11.55 below is at a distance of 5 cm from it's vertex. If the mirror is 45 cm deep, find the distance AB.

Fig.11.55

Solution:
1. From fig.11.55, it is clear that:
    ♦ Vertex of the mirror is at the origin O.
    ♦ Axis of the mirror lies along the x-axis.
    ♦ The parabola opens to the right.
2. So we can draw a rough sketch of the graph of the parabola as shown in fig.11.56 below:

Fig.11.56

3. General equation of the parabola in the above fig.11.56 is: y² = 4ax
• Given that, F is at a distance of 5 cm from the vertex. So we get: a = 5 cm.
• So the equation of the parabola is: y² = 4 × 5 × x = 20x
4. In fig.11.55, 'A' is a point on the parabola. It is at a horizontal distance of 45 cm from the y=axis.
• So the coordinates of 'A' can be written as (45,y) 
5. 'B' is also at a distance of 45 cm from the y-axis.
• So 'A' and 'B' are symmetrical points. The coordinates of B can be written as (45,-y)
6. Since A(45,y) is a point on the parabola, we can substitute those coordinates in the equation of the parabola obtained in (3).
• We get: y² = 20 × 45 = 900
• From this we get: y = 30 or -30
7. So the coordinates of point A are (45,30)
• Also, the coordinates of B are (45,-30)
8. Using the coordinates, we get:
Distance AB  = $\sqrt{(45 - 45)^2 + (-30 - 30)^2}~=~\sqrt{60^2} = 60$ cm.

Solved example 11.19
The distance between the supports of a beam is 12 metres. When loads are applied on the beam, it deflects and becomes parabolic in shape. The maximum deflection of 3 cm occurs at the midpoint between the supports. At what point between the supports, does a deflection of 1 cm occur?
Solution:
1. The situation before deflection is shown in fig.11.57(a) below:

Fig.11.57

     
• The beam is represented by the red horizontal line AB.
2. After deflection, the the midpoint O of the beam is at a vertical distance of 3 cm below the horizontal line. This is shown in fig.11.57(b).
• Let C be the point where the deflection is 1 cm. Then C will be at a vertical distance of 2 cm above O
3. Given that, the deflected beam is in the shape of a parabola.
• We can consider the lowest point ‘O’ as the vertex.
4. So we can draw a rough sketch of the graph of the parabola as shown in fig.11.58 below:

Fig.11.58

• Vertex of the parabola is at the origin O. This vertex is the midpoint of the beam.
• A is at a distance of 6 m to the left of midpoint. Also, A is 3 cm (0.03 m) vertically above O.
    ♦ So the coordinates of A are: (-6,0.03)
• B is at a distance of 6 m to the right of midpoint. Also, B is 3 cm (0.03 m) vertically above O.
    ♦ So the coordinates of B are: (6,0.03)
• C is at an unknown distance. It is represented by ‘x’. Also, C is 2 cm (0.02 m) vertically above O.
    ♦ So the coordinates of C are (x,0.02)
5. The parabola in fig.11.58 is of the form x² = 4ay
6. A(-6,0.03) is a point on the parabola. So substituting the coordinates in (5), we get:
(-6)² = 4 × a × 0.03
⇒ 36 = 0.12a
⇒ a = 300
7. So the equation of the parabola is: x² = 4 × 300y = 1200y
8. Substituting the coordinates of C in the above equation, we get:
x² = 1200 × 0.02 = 24
⇒ x = √24 = 2√6
9. So we can write:
Deflection of 1 cm, occurs at a distance of 2√6 m from the midpoint of the beam.

Solved example 11.20
A rod AB of length 15 cm rests in between two coordinate axes in such a way that the end point A lies on x-axis and end point B lies on y-axis. A point P(x,y) is taken on the rod in such a way that AP = 6 cm. Show that the locus of P is an ellipse.
Solution:
1. In fig.11.59 below, the rod AB is resting between OX and OY.

Fig.11.59

• AB makes an angle 𝜃 with OX.
• End A is on OX. End B is on OY.
• P is a point on the rod.
    ♦ Distance of P from A is 6 cm.
    ♦ Distance of P from B is 9 cm.
2. Horizontal and vertical dashed lines:
• A horizontal dashed line is drawn through P. This line intersects the y-axis at Q.
• A vertical dashed line is drawn through P. This line intersects the x-axis at R.
3. Since OX and PQ are parallel, ∠ QPB = 𝜃
4. Let the coordinates of P be (x,y)
    ♦ Then PQ wil be equal to x.
    ♦ Also PR will be equal to y.
5. Now we take trigonometric ratios:
(i) Consider ⧍PBQ.
• In this triangle, cos 𝜃 = x/9.
(ii) Consider ⧍PAR.
• In this triangle, sin 𝜃 = y/6
6. We have the identity: cos²𝜃 + sin²𝜃 = 1
• Substituting the values from (5), we get:

$\begin{array}{ll}
{}&{\left(\frac{x}{9} \right)^2 + \left(\frac{x}{9} \right)^2}
& {~=~}& {1}
&{} \\

{\Rightarrow}&{\frac{x^2}{81} + \frac{y^2}{36}}
& {~=~}& {1}
&{} \\

\end{array}$
7. This is the equation of an ellipse. Any values of (x,y) which the point P takes, will fall on the ellipse.
• So we can write:
Locus of point P is the ellipse $\frac{x^2}{81} + \frac{y^2}{36} = 1$.

◼ More details can be written in 3 steps:
1. The locus is the path traced by a moving point.
• The movement of the point must satisfy one or more specified conditions.
2. In our present problem, P is the point which moves.
The conditions are:
(i) Point A must always be on the x-axis.
(ii) Point B must always be on the y-axis.
(iii) Point P must always be:
    ♦ on the line connecting A and B..
    ♦ 6 cm away from A.  
    ♦ 9 cm away from B.
3. All conditions specified in (2) are satisfied in the animation in fig.11.60 below:

Fig.11.60

• We see that:
The path traced by P is the ellipse $\frac{x^2}{81} + \frac{y^2}{36} = 1$

---

Link to a few more solved examples is given below:

Miscellaneous Exercise

---

In the next chapter, we will see Three dimensional geometry.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 11.13 - Solved Examples on Hyperbola

In the previous section, we saw latus rectum of hyperbola. We also saw a solved example. In this section, we will see a few more solved examples.

Solved example 11.15
Find the equation of the hyperbola with foci (0,±3) and vertices $\left(0,\pm \frac{\sqrt{11}}{2} \right)$
Solution:
1. The given foci are: (0,3) and (0,-3)
   ♦ These foci lie on the y-axis.
• So the equation of the hyperbola is of the form: $\frac{y^2}{a^2}~-~\frac{x^2}{b^2}~=~1$
2. Since the foci are (0,3) and (0,-3), we get: c = 3
3. The given vertices are: $\left(0, \frac{\sqrt{11}}{2} \right),~\left(0, -\frac{\sqrt{11}}{2} \right)$
• So we get: a = $\frac{\sqrt{11}}{2}$
4. Now we have 'a' and 'c'. We can calculate 'b'.
• We have: c² = a² + b².
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{3^2}
& {~=~}& {\left(\frac{\sqrt{11}}{2} \right)^2~+~b^2}
&{} \\

{\Rightarrow}&{9}
& {~=~}& {\frac{11}{4}~+~b^2}
&{} \\

{\Rightarrow}&{b^2}
& {~=~}& {9~-~\frac{11}{4}}
&{} \\

{\Rightarrow}&{b^2}
& {~=~}& {\frac{25}{4}}
&{} \\

{\Rightarrow}&{b}
& {~=~}& {\frac{5}{2}}
&{} \\

\end{array}$

• So the value of b is $\frac{5}{2}$ units.

5. Now we have 'a' and 'b'.
• Based on step (1), we can write:
Equation of the hyperbola is: $\frac{y^2}{\left(\frac{\sqrt{11}}{2} \right)^2}~-~\frac{x^2}{\left(\frac{5}{2} \right)^2}~=~1$
• This can be simplified as follows:

$\begin{array}{ll}
{}&{\frac{y^2}{\left(\frac{\sqrt{11}}{2} \right)^2}~-~\frac{x^2}{\left(\frac{5}{2} \right)^2}}
& {~=~}& {1}
&{} \\

{\Rightarrow}&{\frac{y^2}{\frac{11}{4}}~-~\frac{x^2}{\frac{25}{4}}}
& {~=~}& {1}
&{} \\

{\Rightarrow}&{\frac{4 y^2}{11}~-~\frac{4 x^2}{25}}
& {~=~}& {1}
&{} \\

{\Rightarrow}&{100 y^2~-~44 x^2}
& {~=~}& {275}
&{} \\

\end{array}$

Solved example 11.16
Find the equation of the hyperbola with foci (0,±12) and length of latus rectum 36.
Solution:
1. The given foci are: (0,12) and (0,-12)
   ♦ These foci lie on the y-axis.
• So the equation of the hyperbola is of the form: $\frac{y^2}{a^2}~-~\frac{x^2}{b^2}~=~1$
2. Since the foci are (0,12) and (0,-12), we get: c = 12
3. We have: Length of latus rectum = $\frac{2 b^2}{a}$ = 36
• From this, we get:
$\begin{array}{ll}
{}&{36}
& {~=~}& {\frac{2 × b^2}{a}}
&{} \\

{\Rightarrow}&{18}
& {~=~}& {\frac{b^2}{a}}
&{} \\

{\Rightarrow}&{b^2}
& {~=~}& {18a}
&{} \\

\end{array}$

4. Now we have 'b²' in terms of 'a' . We can calculate 'a'.
• We have: c² = a² + b².
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{12^2}
& {~=~}& {a^2~+~18 a}
&{} \\

{\Rightarrow}&{144}
& {~=~}& {a^2~+~18a}
&{} \\

{\Rightarrow}&{a^2~+~18a~-~144}
& {~=~}& {0}
&{} \\

\end{array}$

• Solving this quadratic equation, we get: a = 6 or a = -24.
'a' is a length. It cannot be -ve. So we can write: a = 6

5. From the result in (3), we get: b² = 18a = 18 × 6 = 108

6. Now we have 'a' and 'b²'.
• Based on step (1), we can write:
Equation of the hyperbola is: $\frac{y^2}{36}~-~\frac{x^2}{108}~=~1$

Solved example 11.17
If the foci of the ellipse $\frac{x^2}{25}~+~\frac{y^2}{k^2}~=~1$ and the hyperbola $\frac{x^2}{144}~-~\frac{y^2}{81}~=~\frac{1}{25}$ coincide, find the value of k.
Solution:
1. We are given the complete equation of the hyperbola. So we will analyze it first.
• Given equation of the hyperbola is: $\frac{x^2}{144}~-~\frac{y^2}{81}~=~\frac{1}{25}$.
• It can be rearranged as follows:
$\begin{array}{ll}
{}&{\frac{x^2}{144}~-~\frac{y^2}{81}}
& {~=~}& {\frac{1}{25}}
&{} \\

{\Rightarrow}&{\frac{25 x^2}{144}~-~\frac{25 y^2}{81}}
& {~=~}& {\frac{25}{25}}
&{} \\

{\Rightarrow}&{\frac{x^2}{144/25}~-~\frac{y^2}{81/25}}
& {~=~}& {1}
&{} \\

{\Rightarrow}&{\frac{x^2}{(12/5)^2}~-~\frac{y^2}{(9/5)^2}}
& {~=~}& {1}
&{} \\

\end{array}$

2. In the above result, x² is the +ve term. So we can write:
The given hyperbola is of the form: $\frac{x^2}{a^2}~-~\frac{y^2}{b^2}~=~1$ 
• Thus we get: a = 12/5 and b = 9/5
3. For any hyperbola, we have: c² = a² + b².
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{c^2}
& {~=~}& {\left(\frac{12}{5} \right)^2~+~\left(\frac{9}{5} \right)^2}
&{} \\

{}&{}
& {~=~}& {\frac{144}{25}~+~\frac{81}{25}}
&{} \\

{}&{}
& {~=~}& {\frac{225}{25}}
&{} \\

\end{array}$

• So the value of c is 15/5 = 3

4. The foci are (-c,0) and (c,0)
• So we get: (-3,0) and (3,0)

5. Given that, foci of the ellipse and the hyperbola are the same. So we can write:
• Foci of the ellipse $\frac{x^2}{25}~+~\frac{y^2}{k^2}~=~1$ are: (-3,0) and (3,0)
• Thus we can write: Value of 'c' for the ellipse is 3.   
6. Given equation of the ellipse is: $\frac{x^2}{25}~+~\frac{y^2}{k^2}~=~1$
• This is of the form: $\frac{x^2}{a^2}~+~\frac{y^2}{b^2}~=~1$
• So we can write: a = 5 and b = k
7. For any ellipse, we have: c² = a² - b².
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{3^2}
& {~=~}& {5^2~-~k^2}
&{} \\

{\Rightarrow}&{k^2}
& {~=~}& {5^2~-~3^2}
&{} \\

{\Rightarrow}&{k^2}
& {~=~}& {25~-~9}
&{} \\

{\Rightarrow}&{k^2}
& {~=~}& {16}
&{} \\

{\Rightarrow}&{k}
& {~=~}& {4}
&{} \\

\end{array}$

8. So we can write:
   ♦ The ellipse $\frac{x^2}{25}~+~\frac{y^2}{4^2}~=~1$
   ♦ And the hyperbola $\frac{x^2}{144}~-~\frac{y^2}{81}~=~\frac{1}{25}$
   ♦ Have the same foci (-3,0) and (3,0).
9. The actual plot is shown in fig.11.54 below:

Fig.11.54

 

---

Link to a few more solved examples is given below:

Exercise 11.4

---

In the next section, we will see some miscellaneous examples.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 11.12 - Latus Rectum of Hyperbola

In the previous section, we completed a discussion on the standard equations of hyperbola. In this section, we will see latus rectum of hyperbola.

Latus rectum of a hyperbola

This can be explained in three steps:
1. Latus rectum is a line segment.
2. If a line segment is to qualify as the latus rectum of a hyperbola, it must satisfy three conditions.
(i) It must pass through F₁ or F₂.
(ii) It must be perpendicular to the transverse axis.
(iii) It’s end points must lie on the hyperbola.
3. Line segments AB and CD in fig.11.52 below satisfy all three conditions. So both are latus rectum of that hyperbola.

Fig.11.52

 

---

Length of the latus rectum

• We have seen the two forms where the equation of hyperbola is the simplest. Length of the latus rectum can be calculated very easily for those two forms.

• Let us see Form 1. It is shown in fig.11.52 above. We want the length AB. It can be calculated in 2 steps:
1. In the fig.11.52 above, let the length AF₂ be l.
• Then the coordinates of A will be (c,l)
2. Point A lies on the hyperbola. So we can write:

$\begin{array}{ll}
{}&{\frac{c^2}{a^2}~-~\frac{l^2}{b^2}}
& {~=~}& {1}
&{} \\

{\Rightarrow}&{\frac{l^2}{b^2}}
& {~=~}& {\frac{c^2}{a^2}~-~1}
&{} \\

{\Rightarrow}&{\frac{l^2}{b^2}}
& {~=~}& {\frac{a^2~+~b^2}{a^2}~-~1}
&{} \\

{\Rightarrow}&{\frac{l^2}{b^2}}
& {~=~}& {\frac{a^2}{a^2}~+~\frac{b^2}{a^2}~-~1}
&{} \\

{\Rightarrow}&{\frac{l^2}{b^2}}
& {~=~}& {1~+~\frac{b^2}{a^2}~-~1}
&{} \\

{\Rightarrow}&{\frac{l^2}{b^2}}
& {~=~}& {\frac{b^2}{a^2}}
&{} \\

{\Rightarrow}&{l^2}
& {~=~}& {\frac{b^4}{a^2}}
&{} \\

{\Rightarrow}&{l}
& {~=~}& {\frac{b^2}{a}}
&{} \\

{\Rightarrow}&{2l}
& {~=~}& {\frac{2b^2}{a}}
&{} \\

\end{array}$

• Note:
In the above calculation, first we obtained l. Then we doubled it to obtain the total length AB. This is because, the hyperbola is symmetric about the transverse axis.

◼ So we can write:
Length of the latus rectum of the hyperbola $\frac{x^2}{a^2}~-~\frac{y^2}{b^2}~=~1$ is  $\frac{2 b^2}{a}$

---

• Let us see Form 2. It is shown in fig.11.53 below:

Fig.11.53

• We want the length AB. It can be calculated in 2 steps:
1. In the fig.11.53 above, let the length AF₁ be l.
Then the coordinates of A will be (-l,c)
2. Point A lies on the hyperbola. So we can write:

$\begin{array}{ll}
{}&{\frac{c^2}{a^2}~-~\frac{(-l)^2}{b^2}}
& {~=~}& {1}
&{} \\

{}&{\frac{c^2}{a^2}~-~\frac{l^2}{b^2}}
& {~=~}& {1}
&{} \\

{\Rightarrow}&{\frac{l^2}{b^2}}
& {~=~}& {\frac{c^2}{a^2}~-~1}
&{} \\

{\Rightarrow}&{\frac{l^2}{b^2}}
& {~=~}& {\frac{a^2~+~b^2}{a^2}~-~1}
&{} \\

{\Rightarrow}&{\frac{l^2}{b^2}}
& {~=~}& {1~+~\frac{b^2}{a^2}~-~1}
&{} \\

{\Rightarrow}&{l^2}
& {~=~}& {\frac{b^4}{a^2}}
&{} \\

{\Rightarrow}&{l}
& {~=~}& {\frac{b^2}{a}}
&{} \\

{\Rightarrow}&{2l}
& {~=~}& {\frac{2b^2}{a}}
&{} \\

\end{array}$

• Note:
In the above calculation, first we obtained l. Then we doubled it to obtain the total length AB. This is because, the hyperbola is symmetric about the transverse axis.

◼ So we can write:
Length of the latus rectum of the hyperbola $\frac{y^2}{a^2}~-~\frac{x^2}{b^2}~=~1$ is also  $\frac{2 b^2}{a}$

---

Now we will see a solved example:

Solved example 11.14
For the hyperbolas:
(a) $\frac{x^2}{9}~-~\frac{y^2}{16}~=~1$
(b) y² - 16x² = 16
find the following:
(i) coordinates of the foci
(ii) coordinates of the vertices
(iii) the eccentricity
(iv) length of the latus rectum.
Solution:
Part (a):
1. x² has the +ve term.
• So the equation of the hyperbola is of the form: $\frac{x^2}{a^2}~-~\frac{y^2}{b^2}~=~1$
• So we can write:
    ♦ Transverse axis of this hyperbola lies along the x-axis.
    ♦ Conjugate axis of this hyperbola lies along the y-axis.
    ♦ a² = 9. So a = 3
    ♦ b² = 16. So b = 4
2. We have: c² = a² + b².
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{c^2}
& {~=~}& {3^2~+~4^2}
&{} \\

{}&{}
& {~=~}& {9~+~16}
&{} \\

{}&{}
& {~=~}& {25}
&{} \\

\end{array}$

• So the value of c is 5

3. The coordinates of the foci are (-c,0) and (c,0)
• So in our present case, the coordinates are: (-5,0) and (5,0)
• This is the answer for part (i).
4. The coordinates of the vertices are (-a,0) and (a,0)
• So in our present case, the coordinates are: (-3,0) and (3,0)
• This is the answer for part (ii).
5. Eccentricity is given by: e = c/a
• So in our present case, e = 5/3
• This is the answer for part (iii).
6. We have: Length of latus rectum = $\frac{2 b^2}{a}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\text{Length}}
& {~=~}& {\frac{2 × 4^2}{3}}
&{} \\

{}&{}
& {~=~}& {\frac{32}{3}~\text{units}}
&{} \\

\end{array}$
• This is the answer for part (iv).

Part (b):
• The given equation is y² - 16x² = 16.
   ♦ Numerator of the coefficient of x² must be 1.
   ♦ Numerator of the coefficient of y² must be 1.
   ♦ Right side of the equation must be 1.
• So we divide the given equation by 16. We get: $\frac{y^2}{16}~-~\frac{x^2}{1}~=~1$
1. y² has the +ve term.
• So the equation of the hyperbola is of the form: $\frac{y^2}{a^2}~-~\frac{x^2}{b^2}~=~1$
• So we can write:
    ♦ Transverse axis of this hyperbola lies along the y-axis.
    ♦ Conjugate axis of this hyperbola lies along the x-axis.
    ♦ a² = 16. So a = 4
    ♦ b² = 1. So b = 1
2. We have: c² = a² + b².
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{c^2}
& {~=~}& {4^2~+~^2}
&{} \\

{}&{}
& {~=~}& {16~+~1}
&{} \\

{}&{}
& {~=~}& {17}
&{} \\

\end{array}$

• So the value of c is √17

3. The coordinates of the foci are (0,-c) and (0,c)
• So in our present case, the coordinates are: (0,-√17) and (0,√17)
• This is the answer for part (i).
4. The coordinates of the vertices are (-a,0) and (a,0)
• So in our present case, the coordinates are: (0,-4) and (0,4)
• This is the answer for part (ii).
5. Eccentricity is given by: e = c/a
• So in our present case, e = (√17)/4
• This is the answer for part (iii).
6. We have: Length of latus rectum = $\frac{2 b^2}{a}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\text{Length}}
& {~=~}& {\frac{2 × 1^2}{4}}
&{} \\

{}&{}
& {~=~}& {\frac{1}{2}~\text{units}}
&{} \\

\end{array}$
• This is the answer for part (iv).

---

In the next section, we will see a few more solved examples.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 11.11 - Another Simplest Equation of Hyperbola

In the previous section, we saw the simplest equation of a hyperbola.
    ♦ The center was at O.
    ♦ The transverse axis was along the x-axis.
    ♦ The conjugate axis was along the y-axis.

• To write the equation of a hyperbola, we must first place it on the Cartesian plane.
• The equation will be in the simplest form also when the following three conditions are satisfied:
    ♦ The center is at O.
    ♦ The transverse axis lies along the y-axis.
    ♦ The conjugate axis lies along the x-axis.
• This is shown in fig.11.48 below:

Fig.11.48

• Based on fig.11.48, we can derive the equation in 6 steps:
1. Let P(x,y) be any point on the hyperbola.
2. We know that, F₁ is at a distance of ‘c’ from O.
• So the coordinates of F₁ will be (0,c)   
3. We know that, F₂ is at a distance of ‘c’ from O.
• So the coordinates of F₂ will be (0,-c)
4. Now we have three points and their coordinates:
P(x,y), F₁(0,c), F₂(0,-c)
• Using the distance formula, we can write some distances:

• First we write the distance PF₁:
$\begin{array}{ll}
{}&{PF_1}
& {~=~}& {\sqrt{(x~-~ 0)^2~+~(y - c)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{x^2~+~(y-c)^2}}
&{} \\

\end{array}$ 

• Next we write the distance PF₂:
$\begin{array}{ll}
{}&{PF_2}
& {~=~}& {\sqrt{(x~-~ 0)^2~+~(y~-~-c)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{x^2~+~(y+c)^2}}
&{} \\

\end{array}$

• Difference of the above two distances is: $\sqrt{x^2~+~(y-c)^2}~-~\sqrt{x^2~+~(y+c)^2}$

5. We know that, the constant difference for a hyperbola is '2a'

6. Equating the results in (4) and (5), we get:

$\begin{array}{ll}
{}&{\sqrt{x^2~+~(y-c)^2}~-~\sqrt{x^2~+~(y+c)^2}}
& {~=~}& {2a}
&{} \\

{\Rightarrow}&{\sqrt{x^2~+~(y-c)^2}}
& {~=~}& {2a~+~\sqrt{x^2~+~(y+c)^2}}
&{} \\

{\Rightarrow}&{x^2~+~(y-c)^2}
& {~=~}& {4a^2~+~4a \sqrt{x^2~+~(y+c)^2}~+~x^2~+~(y+c)^2~~ \color {green} {\text{- - - (I)}}}
&{} \\

{\Rightarrow}&{x^2 + y^2 - 2yc + c^2}
& {~=~}& {4a^2~+~4a \sqrt{x^2~+~(y+c)^2}~+~x^2 + y^2 + 2yc + c^2}
&{} \\

{\Rightarrow}&{-2yc}
& {~=~}& {4a^2~+~4a \sqrt{x^2~+~(y+c)^2} + 2yc}
&{} \\

{\Rightarrow}&{-4yc}
& {~=~}& {4a^2~+~4a \sqrt{x^2~+~(y+c)^2}}
&{} \\

{\Rightarrow}&{-yc}
& {~=~}& {a^2~+~a \sqrt{x^2~+~(y+c)^2}~~ \color {green} {\text{- - - (II)}}}
&{} \\

{\Rightarrow}&{-\frac{yc}{a}}
& {~=~}& {a~+~\sqrt{x^2~+~(y+c)^2}}
&{} \\

{\Rightarrow}&{\sqrt{x^2~+~(y+c)^2}}
& {~=~}& {a~+~\frac{yc}{a}~~ \color {green} {\text{- - - (III)}}}
&{} \\

{\Rightarrow}&{x^2~+~(y+c)^2}
& {~=~}& {a^2~+~\frac{2ayc}{a}~+~\frac{y^2 c^2}{a^2}}
&{} \\

{\Rightarrow}&{x^2~+~(y+c)^2}
& {~=~}& {a^2~+~2yc~+~\frac{y^2 c^2}{a^2}}
&{} \\

{\Rightarrow}&{x^2 + y^2 + 2yc + c^2}
& {~=~}& {a^2~+~2yc~+~\frac{y^2 c^2}{a^2}}
&{} \\

{\Rightarrow}&{x^2 + y^2 + c^2}
& {~=~}& {a^2 + \frac{y^2 c^2}{a^2}}
&{} \\

{\Rightarrow}&{x^2 ~+~y^2~-~\frac{y^2 c^2}{a^2}}
& {~=~}& {a^2 - c^2}
&{} \\

{\Rightarrow}&{x^2 ~+~y^2 \left(1~-~\frac{c^2}{a^2} \right)}
& {~=~}& {a^2 - c^2}
&{} \\

{\Rightarrow}&{x^2 ~+~y^2 \left(\frac{a^2~-~c^2}{a^2} \right)}
& {~=~}& {a^2 - c^2~~ \color {green} {\text{- - - (IV)}}}
&{} \\

{\Rightarrow}&{-x^2 ~+~y^2 \left(\frac{c^2~-~a^2}{a^2} \right)}
& {~=~}& {c^2 - a^2~~ \color {green} {\text{- - - (V)}}}
&{} \\

{\Rightarrow}&{-x^2 ~+~y^2 \left(\frac{b^2}{a^2} \right)}
& {~=~}& {b^2~~ \color {green} {\text{- - - (VI)}}}
&{} \\

{\Rightarrow}&{\frac{y^2}{a^2}~-~\frac{x^2}{b^2}}
& {~=~}& {1}
&{} \\

\end{array}$

◼ Remarks:
• Line marked as (I):
In this line, we square both sides.
• Line marked as (II):
In this line, we divide both sides by 4.
• Line marked as (III):
In this line, we square both sides.
• Line marked as (IV):
In this line, we multiply both sides by -1.
• Line marked as (V):
In this line, we write b² in the place of c² - a².
• Line marked as (VI):
In this line, we divide both sides by b².

---

Using the above 6 steps, we derived an equation. Now we will prove the converse. It can be written in 8 steps:

1. We derived an equation: $\frac{y^2}{a^2} - \frac{x^2}{b^2}~=~1$
2. To prove the converse, we assume a point P.
• Let P(x,y) be any point on the hyperbola.
• Distance of P from F₁ can be written as:

$\begin{array}{ll}
{}&{PF_1}
& {~=~}& {\sqrt{(x~-~ 0)^2~+~(y - c)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{x^2~+~(y-c)^2}}
&{} \\

\end{array}$

3. But based on the equation written in (1), we can write:

$\begin{array}{ll}
{}&{\frac{x^2}{b^2}}
& {~=~}& {\frac{y^2}{a^2}-1}
&{} \\

{\Rightarrow}&{x^2}
& {~=~}& {b^2\left(\frac{y^2}{a^2}- 1 \right)}
&{} \\

\end{array}$

4. Substituting the above result in (2), we get:

$\begin{array}{ll}
{}&{PF_1}
& {~=~}& {\sqrt{x^2~+~(y-c)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{b^2\left(\frac{y^2}{a^2}-1 \right)~+~(y-c)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{\left(c^2 - a^2 \right)  \left(\frac{y^2}{a^2}-1 \right)~+~(y-c)^2}~~ \color {green} {\text{- - - (I)}}}
&{} \\

{}&{}
& {~=~}& {\sqrt{\frac{c^2 y^2}{a^2} - c^2  - y^2 + a^2 ~+~y^2 - 2yc + c^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{\frac{c^2 y^2}{a^2} + a^2  - 2yc }}
&{} \\

{}&{}
& {~=~}& {\sqrt{\left( a - \frac{cy}{a} \right)^2}}
&{} \\

{}&{}
& {~=~}& {a - \frac{cy}{a}}
&{} \\

\end{array}$

◼ Remarks:
• Line marked as (I):
In this line, we write c² - a² in the place of b².

5. Now we consider the distance of P from F₂. It can be written as:

$\begin{array}{ll}
{}&{PF_2}
& {~=~}& {\sqrt{(x~-~ 0)^2~+~(y~-~-c)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{x^2~+~(y+c)^2}}
&{} \\

\end{array}$

6. As we did in the case of PF₁, here also, we substitute for x². We get:

$\begin{array}{ll}
{}&{PF_2}
& {~=~}& {\sqrt{x^2~+~(y+c)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{b^2\left(\frac{y^2}{a^2}-1 \right)~+~(y+c)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{\left(c^2 - a^2 \right)  \left(\frac{y^2}{a^2}-1 \right)~+~(y+c)^2}~~ \color {green} {\text{- - - (I)}}}
&{} \\

{}&{}
& {~=~}& {\sqrt{ \frac{c^2 y^2}{a^2} - c^2 - y^2 + a^2~+~y^2 + 2yc + c^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{\frac{c^2 y^2}{a^2} + a^2 + 2yc}}
&{} \\

{}&{}
& {~=~}& {\sqrt{\left( a + \frac{cy}{a} \right)^2}}
&{} \\

{}&{}
& {~=~}& {a + \frac{cy}{a}}
&{} \\

\end{array}$

◼ Remarks:
• Line marked as (I):
In this line, we write c² - a² in the place of b². 

7. Now we have to find the difference between PF₁ and PF₂. It can be calculated in 6 steps:
(i) We know that, the vertices are at a distance of 'a' from O.
• So we can draw the horizontal lines y= a and y = -a through the vertices. This is shown in fig.11.49 below:

Fig.11.49

(ii) Our point P is on the top branch of the hyperbola.
• That means, P is above the line y=a
    ♦ So the y-coordinate of P will be greater than 'a'.
    ♦ We can write: y > a
(iii) Now, $\frac{c}{a}$ is greater than '1' because, 'c' is always greater than 'a'.
    ♦ Since $\frac{c}{a}$ is greater than '1', and y>a, we can write: $\frac{cy}{a}$ is greater than 'a'.
(iv) So the distance PF₁ = $a-\frac{cy}{a}$ will become -ve
• To make it +ve, we must write: PF₁ = $\frac{cy}{a}-a$
(v) The distance PF₂ = $a+\frac{cy}{a}$ need not be adjusted because, subtraction is not involved. 
(vi) Now we can write the difference:
• Since PF₂ is larger, we must subtract PF₁ from PF₂.
PF₂ - PF₁ = $a+\frac{cy}{a}~-~\left( \frac{cy}{a}-a \right)$
= $a+\frac{cy}{a} -  \frac{cy}{a}+ a$ = 2a
8. In the step (7) above, we considered the case when the point P is on the top branch of the hyperbola.
• Fig.11.50 below shows the case when P is on the bottom branch.

Fig.11.50

• Here also, to find the difference, we must make some adjustments. It can be written in 6 steps:
(i) We know that, the vertices are at a distance of 'a' from O.
• So we can draw the horizontal lines y= -a and y = a through the vertices. This is shown in fig.11.50 above.
(ii) Our point P is on the bottom branch of the hyperbola.
• That means, P is below the line y=-a
    ♦ So the y-coordinate of P will be lesser than '-a'.
    ♦ We can write: y will be -ve
(iii) Since y is -ve, the distance PF₁ = $a-\frac{cy}{a}$ will become +ve. So there is no adjustment required for PF₁
(iv) Now consider PF₂ = $a+\frac{cy}{a}$
• $\frac{c}{a}$ is greater than '1' because, 'c' is always greater than 'a'.
    ♦ Since $\frac{c}{a}$ is greater than '1', and 'y' is -ve, we can write: $\frac{cy}{a}$ is -ve and numerically greater than 'a'.
(v) So the distance PF₂ = $a+\frac{cy}{a}$ will become -ve
• To make it +ve, we must write: PF₂ = $-\left(a+\frac{cy}{a} \right)$
(vi) Now we can write the difference:
• Since PF₁ is larger, we must subtract PF₂ from PF₁.
PF₁ - PF₂ = $\left(a-\frac{cy}{a}\right)~-~-\left(a+\frac{cy}{a} \right)$
= $a - \frac{cy}{a}+ a + \frac{cy}{a}$ = 2a
9. Based on steps (7) and (8), we can write:
The point P can be anywhere on the hyperbola. The difference will always be '2a'.
10. In the previous section, we saw that, the constant difference of the hyperbola is '2a'.
11. So any point P(x,y) on the hyperbola will satisfy the equation $\frac{y^2}{a^2}~-~\frac{x^2}{b^2}~=~1$
• The converse is proved.

◼ So we can write:
If the center of the hyperbola is at O, transverse axis lies along the y-axis and conjugate axis lies along the x-axis, then equation of the hyperbola is: $\frac{y^2}{a^2}~-~\frac{x^2}{b^2}~=~1$

---

Based on the above equation of the hyperbola, we can write an interesting fact. It can be written in 4 steps:
1. We have: $\frac{y^2}{a^2}~-~\frac{x^2}{b^2}~=~1$
2. This can be rearranged as: $\frac{y^2}{a^2}~=~1~+~\frac{x^2}{b^2}$
• So $\frac{y^2}{a^2}$ will be always greater than 1.
• That is: $\left|\frac{y}{a}\right|~\ge~1$
3. Solving the above inequality, we get:
    ♦ y should not be greater than -a.
    ♦ y should not be less than a.
• That is: $y \le -a ~\text{or}~y \ge a$
4. So we can write:
• Consider any point on the hyperbola. It will not lie between the two horizontal lines:
    ♦ y = -a.
    ♦ y =  a.

---

• So we have seen the two simplest forms of the hyperbola. Let us write a comparison between the two forms:
A. Comparison based on orientation:
• This can be written in 5 steps:
1. In the first form,
    ♦ Transverse axis lies along the x-axis.
    ♦ Conjugate axis lies along the y-axis.
2. In the second form,
    ♦ Transverse axis lies along the y-axis.
    ♦ Conjugate axis lies along the x-axis.
3. Whatever be the orientation,
    ♦ Length of semi-transverse axis is denoted by the letter ‘a’.
    ♦ Length of semi-conjugate axis is denoted by the letter ‘b'.
4. Equations of the two orientations:
    ♦ For the first form, the equation is: $\frac{x^2}{a^2}~-~\frac{y^2}{b^2}~=~1$
    ♦ For the second form, the equation is: $\frac{y^2}{a^2}~-~\frac{x^2}{b^2}~=~1$
• These are known as the standard equations of the hyperbola.
5. A hyperbola in which 'a' and 'b' are same, is called an equilateral hyperbola.
B. Comparison of coefficients:
• This can be written in 2 steps:
1. For the first form, $\frac{1}{a^2}$ is the coefficient of x²
    ♦ Here x² is the +ve term.
2. For the second form, $\frac{1}{a^2}$ is the coefficient of y²
    ♦ Here y² is the +ve term.
◼ So in the given equation,    
• If x² is the +ve term, then the transverse axis of the hyperbola lies along the x-axis.
• If y² is the +ve term, then the transverse axis of the hyperbola lies along the y-axis.
C. Comparison based on symmetry:
• This can be written in 3 steps:
1. Whatever be the orientation, the hyperbola will be symmetric about the transverse axis and conjugate axis.
2. This is because, the x and y values are being squared.
    ♦ +ve x and -ve x give the same result.
    ♦ +ve y and -ve y give the same result.
3. So four symmetric combinations are possible:
(x,y), (-x,y), (x,-y) and (-x,-y).
• An example is shown in fig.11.51 below:

Fig.11.51

---

So we have seen the standard equations of the hyperbola. In the next section, we will see latus rectum of hyperbola.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 11.10 - Simplest Equation of A Hyperbola

In the previous section, we saw the basic properties of a hyperbola. In this section, we will see equation of an hyperbola.

• To write the equation of a hyperbola, we must first place it on the Cartesian plane.
• The equation will be in the simplest form when the following three conditions are satisfied:
    ♦ The center of the hyperbola is at the origin O.
    ♦ The transverse axis of the hyperbola lies along the x-axis.
    ♦ The conjugate axis of the hyperbola lies along the y-axis.
• This is shown in fig.11.45 below:

Fig.11.45

• Based on fig.11.45, we can derive the equation in 6 steps:
1. Let P(x,y) be any point on the hyperbola.
2. We know that, F₁ is at a distance of ‘c’ from O.
• So the coordinates of F₁ will be (-c,0)   
3. We know that, F₂ is at a distance of ‘c’ from O.
• So the coordinates of F₂ will be (c,0)
4. Now we have three points and their coordinates:
P(x,y), F₁(-c,0), F₂(c,0)
• Using the distance formula, we can write some distances:

• First we write the distance PF₁:
$\begin{array}{ll}
{}&{PF_1}
& {~=~}& {\sqrt{(x~-~ -c)^2~+~(y - 0)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(x + c)^2~+~y^2}}
&{} \\

\end{array}$ 

• Next we write the distance PF₂:
$\begin{array}{ll}
{}&{PF_2}
& {~=~}& {\sqrt{(x~-~ c)^2~+~(y - 0)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(x - c)^2~+~y^2}}
&{} \\

\end{array}$

• Difference of the above two distances is: $\sqrt{(x + c)^2~+~y^2}~-~\sqrt{(x - c)^2~+~y^2}$

5. We know that, the constant difference for a hyperbola is '2a'

6. Equating the results in (4) and (5), we get:

$\begin{array}{ll}
{}&{\sqrt{(x + c)^2~+~y^2}~-~\sqrt{(x - c)^2~+~y^2}}
& {~=~}& {2a}
&{} \\

{\Rightarrow}&{\sqrt{(x + c)^2~+~y^2}}
& {~=~}& {2a~+~\sqrt{(x - c)^2~+~y^2}}
&{} \\

{\Rightarrow}&{(x + c)^2~+~y^2}
& {~=~}& {4a^2~+~4a \sqrt{(x - c)^2~+~y^2}~+~(x - c)^2~+~y^2~~ \color {green} {\text{- - - (I)}}}
&{} \\

{\Rightarrow}&{x^2 + 2xc + c^2 + y^2}
& {~=~}& {4a^2~+~4a \sqrt{(x - c)^2~+~y^2}~+~x^2 - 2xc + c^2~+~y^2}
&{} \\

{\Rightarrow}&{2xc}
& {~=~}& {4a^2~+~4a \sqrt{(x - c)^2~+~y^2}- 2xc}
&{} \\

{\Rightarrow}&{4xc}
& {~=~}& {4a^2~+~4a \sqrt{(x - c)^2~+~y^2}}
&{} \\

{\Rightarrow}&{xc}
& {~=~}& {a^2~+~a \sqrt{(x - c)^2~+~y^2}~~ \color {green} {\text{- - - (II)}}}
&{} \\

{\Rightarrow}&{\frac{xc}{a}}
& {~=~}& {a~+~\sqrt{(x - c)^2~+~y^2}}
&{} \\

{\Rightarrow}&{\sqrt{(x - c)^2~+~y^2}}
& {~=~}& {\frac{xc}{a}~-~a~~ \color {green} {\text{- - - (III)}}}
&{} \\

{\Rightarrow}&{(x - c)^2~+~y^2}
& {~=~}& {\frac{x^2 c^2}{a^2}~-~\frac{2axc}{a}~+~a^2}
&{} \\

{\Rightarrow}&{(x - c)^2~+~y^2}
& {~=~}& {a^2~-~2cx~+~\frac{x^2 c^2}{a^2}}
&{} \\

{\Rightarrow}&{x^2 - 2cx + c^2~+~y^2}
& {~=~}& {a^2~-~2cx~+~\frac{x^2 c^2}{a^2}}
&{} \\

{\Rightarrow}&{x^2 + c^2~+~y^2}
& {~=~}& {a^2~+~\frac{x^2 c^2}{a^2}}
&{} \\

{\Rightarrow}&{x^2 ~+~y^2~-~\frac{x^2 c^2}{a^2}}
& {~=~}& {a^2 - c^2}
&{} \\

{\Rightarrow}&{x^2 \left(1~-~\frac{c^2}{a^2} \right)~+~y^2}
& {~=~}& {a^2 - c^2}
&{} \\

{\Rightarrow}&{x^2 \left(\frac{a^2~-~c^2}{a^2} \right)~+~y^2}
& {~=~}& {a^2 - c^2~~ \color {green} {\text{- - - (IV)}}}
&{} \\

{\Rightarrow}&{x^2 \left(\frac{c^2~-~a^2}{a^2} \right)~-~y^2}
& {~=~}& {c^2 - a^2~~ \color {green} {\text{- - - (V)}}}
&{} \\

{\Rightarrow}&{x^2 \left(\frac{b^2}{a^2} \right)~-~y^2}
& {~=~}& {b^2~~ \color {green} {\text{- - - (VI)}}}
&{} \\

{\Rightarrow}&{\frac{x^2}{a^2}~-~\frac{y^2}{b^2}}
& {~=~}& {1}
&{} \\

\end{array}$

◼ Remarks:
• Line marked as (I):
In this line, we square both sides.
• Line marked as (II):
In this line, we divide both sides by 4.
• Line marked as (III):
In this line, we square both sides.
• Line marked as (IV):
In this line, multiply both sides by -1.
• Line marked as (V):
In this line, write b² in the place of c² - a².
• Line marked as (VI):
In this line, we divide both sides by b².

---

Using the above 6 steps, we derived an equation. Now we will prove the converse. It can be written in 11 steps:

1. We derived an equation: $\frac{x^2}{a^2}~-~\frac{y^2}{b^2}~=~1$
2. To prove the converse, we assume a point P.
• Let P(x,y) be any point on the ellipse.
• Distance of P from F₁ can be written as:

$\begin{array}{ll}
{}&{PF_1}
& {~=~}& {\sqrt{(x~-~ -c)^2~+~(y - 0)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(x + c)^2~+~y^2}}
&{} \\

\end{array}$

3. But based on the equation written in (1), we can write:

$\begin{array}{ll}
{}&{\frac{y^2}{b^2}}
& {~=~}& {\frac{x^2}{a^2}-1}
&{} \\

{\Rightarrow}&{y^2}
& {~=~}& {b^2\left(\frac{x^2}{a^2}~-~1 \right)}
&{} \\

\end{array}$

4. Substituting the above result in (2), we get:

$\begin{array}{ll}
{}&{PF_1}
& {~=~}& {\sqrt{(x + c)^2~+~y^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(x + c)^2~+~b^2\left(\frac{x^2}{a^2}~-~1 \right)}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(x + c)^2~+~\left(c^2 - a^2 \right) \left(\frac{x^2 }{a^2}~-~1 \right)}~~ \color {green} {\text{- - - (I)}}}
&{} \\

{}&{}
& {~=~}& {\sqrt{x^2 + 2cx + c^2~+~\frac{c^2 x^2}{a^2} - c^2 - x^2 + a^2 }}
&{} \\

{}&{}
& {~=~}& {\sqrt{2cx~+~a^2 + \frac{c^2 x^2}{a^2}}}
&{} \\

{}&{}
& {~=~}& {\sqrt{\left(a+\frac{cx}{a} \right)^2}}
&{} \\

{}&{}
& {~=~}& {a+\frac{cx}{a}}
&{} \\

\end{array}$

◼ Remarks:
• Line marked as (I):
In this line, we write c² - a² in the place of b².

5. Now we consider the distance of P from F₂. It can be written as:

$\begin{array}{ll}
{}&{PF_2}
& {~=~}& {\sqrt{(x~-~ c)^2~+~(y - 0)^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(x - c)^2~+~y^2}}
&{} \\

\end{array}$

6. As we did in the case of PF₁, here also, we substitute for y². We get:

$\begin{array}{ll}
{}&{PF_2}
& {~=~}& {\sqrt{(x - c)^2~+~y^2}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(x - c)^2~+~b^2\left(\frac{x^2 - a^2}{a^2} \right)}}
&{} \\

{}&{}
& {~=~}& {\sqrt{(x - c)^2~+~\left(c^2 - a^2 \right) \left(\frac{x^2 }{a^2}~-~1 \right)}~~ \color {green} {\text{- - - (I)}}}
&{} \\

{}&{}
& {~=~}& {\sqrt{x^2 - 2cx + c^2~+~\frac{c^2 x^2}{a^2} - c^2 - x^2 + a^2 }}
&{} \\

{}&{}
& {~=~}& {\sqrt{-2cx~+~a^2 + \frac{c^2 x^2}{a^2}}}
&{} \\

{}&{}
& {~=~}& {\sqrt{\left(a-\frac{cx}{a} \right)^2}}
&{} \\

{}&{}
& {~=~}& {a-\frac{cx}{a}}
&{} \\

\end{array}$

◼ Remarks:
• Line marked as (I):
In this line, we write c² - a² in the place of b². 

7. Now we have to find the difference between PF₁ and PF₂. It can be calculated in 6 steps:
(i) We know that, the vertices are at a distance of 'a' from O.
• So we can draw the vertical lines x= -a and x = a through the vertices. This is shown in fig.11.46 below:

Fig.11.46

(ii) Our point P is on the right branch of the hyperbola.
• That means, P is on the right side of the line x=a
    ♦ So the x-coordinate of P will be greater than 'a'.
    ♦ We can write: x > a
(iii) Now, $\frac{c}{a}$ is greater than '1' because, 'c' is greater than 'a'.
    ♦ Since $\frac{c}{a}$ is greater than '1', and x>a, we can write: $\frac{cx}{a}$ is greater than 'a'.
(iv) So the distance PF₂ = $a-\frac{cx}{a}$ will become -ve
• To make it +ve, we must write: PF₂ = $\frac{cx}{a}-a$
(v) The distance PF₁ = $a+\frac{cx}{a}$ need not be adjusted because, subtraction is not involved. 
(vi) Now we can write the difference:
PF₁ - PF₂ = $a+\frac{cx}{a}~-~\left( \frac{cx}{a}-a \right)$
= $a+\frac{cx}{a} -  \frac{cx}{a}+ a$ = 2a
8. In the step (7) above, we considered the case when the point P is on the right side branch of the hyperbola.
• Fig.11.47 below shows the case when P is on the left side branch.

Fig.11.47

• Here also, to find the difference, we must make some adjustments. It can be written in 6 steps:
(i) We know that, the vertices are at a distance of 'a' from O.
• So we can draw the vertical lines x= -a and x = a through the vertices. This is shown in fig.11.47 above.
(ii) Our point P is on the left branch of the hyperbola.
• That means, P is on the left side of the line x=-a
    ♦ So the x-coordinate of P will be lesser than '-a'.
    ♦ We can write: x will be -ve
(iii) Since x is -ve, the distance PF₂ = $a-\frac{cx}{a}$ will become +ve. So there is no adjustment required for PF₂
(iv) Now consider PF₁ = $a+\frac{cx}{a}$
• c/a is greater than '1' because, 'c' is always greater than 'a'.
    ♦ Since $\frac{c}{a}$ is greater than '1', and 'x' is -ve, we can write: $\frac{cx}{a}$ is -ve and numerically greater than 'a'.
(v) So the distance PF₁ = $a+\frac{cx}{a}$ will become -ve
• To make it +ve, we must write: PF₁ = $-\left(a+\frac{cx}{a} \right)$
(vi) Now we can write the difference:
• Since PF₂ is larger, we must subtract PF₁ from PF₂.
PF₂ - PF₁ = $\left(a-\frac{cx}{a}\right)~-~-\left(a+\frac{cx}{a} \right)$
= $a - \frac{cx}{a}+ a + \frac{cx}{a}$ = 2a
9. Based on steps (7) and (8), we can write:
The point P can be anywhere on the hyperbola. The difference will always be '2a'.
10. In the previous section, we saw that, the constant difference of the hyperbola is '2a'.
11. So any point P(x,y) on the hyperbola will satisfy the equation $\frac{x^2}{a^2}~-~\frac{y^2}{b^2}~=~1$
• The converse is proved.

◼ So we can write:
If the center of the hyperbola is at O, transverse axis lies along the x-axis and conjugate axis lies along the y-axis, then equation of the hyperbola is: $\frac{x^2}{a^2}~-~\frac{y^2}{b^2}~=~1$

---

Based on the above equation of the hyperbola, we can write an interesting fact. It can be written in 4 steps:
1. We have: $\frac{x^2}{a^2}~-~\frac{y^2}{b^2}~=~1$
2. This can be rearranged as: $\frac{x^2}{a^2}~=~1~+~\frac{y^2}{b^2}$
• So $\frac{x^2}{a^2}$ will be always greater than 1.
• That is: $\left|\frac{x}{a}\right|~\ge~1$
3. Solving the above inequality, we get:
    ♦ x should not be greater than -a.
    ♦ x should not be less than a.
• That is: $x \le -a ~\text{or}~x \ge a$
4. So we can write:
• Consider any point on the hyperbola. It will not lie between the two vertical lines:
    ♦ x = -a.
    ♦ x =  a.

---

• In this section, we saw a simplest equation of a hyperbola.
    ♦ The center is at O.
    ♦ The transverse axis lies along the x-axis.
    ♦ The conjugate axis lies along the y-axis.
• We will get another simplest equation also when:
    ♦ The center is at O.
    ♦ The transverse axis lies along the y-axis.
    ♦ The conjugate axis lies along the x-axis.
• We will see it in the next section.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 11.9 - Hyperbola

In the previous section, we completed a discussion on ellipse. In this section, we will see hyperbola.

Some basics about hyperbola can be written in 6 steps:
1. Consider the five points F₁, F₂, P₁, P₂ and P₃ marked in fig.11.42 below:

Fig.11.42

2. Let us write some distances:
• Distance of P₁:
   ♦ Distance of P₁ from F₁ is 8.6 units.
   ♦ Distance of P₁ from F₂ is 18.7 units.
         ✰ The difference of the two distances is (18.7 - 8.6) = 10.1 units.
• Distance of P₂:
   ♦ Distance of P₂ from F₁ is 16.7 units.
   ♦ Distance of P₂ from F₂ is 6.6 units.
         ✰ The difference of the two distances is (16.7 - 6.6) = 10.1 units.
• Distance of P₃:
   ♦ Distance of P₃ from F₁ is 14.1 units.
   ♦ Distance of P₃ from F₂ is 4.0 units.
         ✰ The difference of the two distances is (14.1 - 4.0) = 10.1 units.
3. So the three points P₁, P₂ and P₃ have a specialty. It can be written in two steps:
(i) Take any one of those three points.
   ♦ Measure the distance of that point from F₁.
   ♦ Measure the distance of that point from F₂.
(ii) The difference of the two distances will be 10.1 units.
4. There are infinite number of points for which the difference is 10.1 units.      
• All such points will lie in the red curve.
• The red curve is called a hyperbola.
5. So we can write the definition:
A hyperbola is the set of all points in a plane difference of whose distances from two fixed points in the plane is a constant.
6. Note that, for a particular hyperbola, the two points F₁ and F₂ are fixed. If we change one or both of those points, we will get another hyperbola.

---

Now we will see some basic features of hyperbola. They can be written in 8 steps:
1. We have seen that, F₁ and F₂ are two fixed points.
• They are called the foci of the hyperbola.
(‘foci’ is the plural of ‘focus’)
2. Draw a line connecting the two foci.
• Let it intersect the hyperbola at A and B.
• Then the line through the foci is called the transverse axis of the hyperbola.
• This is shown in fig.11.43 below:

Fig.11.43

3. The midpoint of F₁F₂ is called center of the hyperbola. It is denoted by the letter O.
4. Draw a line through O and perpendicular to AB.
• This line is called the conjugate axis of the hyperbola.
5. The points A and B at which the transverse axis meets the hyperbola are called vertices of the hyperbola.
6. The length AB is written as ‘2a’. This is shown in fig.11.44 below:

Fig.11.44

• The distance between the two foci is written as ‘2c’
7. Based on the above fig.11.44, we can write:
   ♦ Distance from center to any one vertex is 'a'.
   ♦ '2a' is the length of the transverse axis.
   ♦ Distance from center to any one focus is 'c'.
8. '2b' is considered as the length of the conjugate axis.
   ♦ Where $b=\sqrt{c^2 - a^2}$

---

In fig.11.42, we saw that, the difference of the distances is a constant. Our next aim is to find the value of that constant. It can be written in 3 steps:
1. Consider a point P on the hyperbola.
• Let it be situated at the vertex A
• Then the distance of P from F₁ = AF₁ = (OF₁ – OA) = c-a
• Also the distance of P from F₂ = AF₂ = (OA + OB + BF₂)
= [a+a+(c-a)] = c + a  
2. So the difference between the distances = [(c+a) – (c-a)] = [c+a-c+a] = 2a
3. We can write:
For any point P on the hyperbola, the difference in distances from the foci will be ‘2a’          

---

Eccentricity of a Hyperbola

This can be explained in 5 steps:
1. Consider the distance ‘c’.
• It is the distance of the focus from the center O.
2. Consider the distance ‘a’.
• It is the distance of the vertex from the center O.
3. Eccentricity of a hyperbola is the ratio of the above two items. It is denoted by the letter ‘e’.
So we can write: $\rm{e=\frac{c}{a}}$
4. Based on this result, we can write: c = ae.
• That means, in any hyperbola, the focus is at a distance of ae from the center.
5. From fig.11.44, it is clear that, 'c' is greater than 'a'. So the eccentricity is never less than 1.

---

In the next section, we will see the standard equations of a hyperbola.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com

Chapter 11.8 - Solved Examples on Ellipse

In the previous section, we saw latus rectum of ellipse. We also saw a solved example. In this section, we will see a few more solved examples.

Solved example 11.10
For the ellipse 9x² + 4y² = 36, find the following:
(i) coordinates of the foci
(ii) coordinates of the vertices
(iii) the length of major axis
(iv) the length of minor axis
(v) the eccentricity
(vi) length of the latus rectum.
Solution:
The given equation can be rearranged as follows:

$\begin{array}{ll}
{}&{9x^2 + 4 y^2}
& {~=~}& {36}
&{} \\

{\Rightarrow}&{\frac{9 x^2}{36}~+~\frac{4 y^2}{36}}
& {~=~}& {\frac{36}{36}}
&{} \\

{\Rightarrow}&{\frac{x^2}{36/9}~+~\frac{y^2}{36/4}}
& {~=~}& {\frac{36}{36}}
&{} \\

{\Rightarrow}&{\frac{x^2}{4}~+~\frac{y^2}{9}}
& {~=~}& {1}
&{} \\

\end{array}$

• Now the equation is in the standard form of an ellipse.
1. Comparing the denominators:
    ♦ Denominator of the x² term is 4
    ♦ Denominator of the y² term is 9
• The larger denominator is taken as a²
• So the equation of the ellipse is of the form: $\frac{x^2}{b^2}~+~\frac{y^2}{a^2}~=~1$
• So we can write:
    ♦ Major axis of this ellipse lies along the y-axis.
    ♦ Minor axis of this ellipse lies along the x-axis.
    ♦ a² = 9. So a = 3
    ♦ b² = 4. So b = 2
2. We have: c² = a² - b².
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{c^2}
& {~=~}& {3^2~-~2^2}
&{} \\

{}&{}
& {~=~}& {9~-~4}
&{} \\

{}&{}
& {~=~}& {5}
&{} \\

\end{array}$

• So the value of c is √5

3. The coordinates of the foci are (0,c) and (0,-c)
• So in our present case, the coordinates are: (0,√5) and (0,-√5)
• This is the answer for part (i).
4. The coordinates of the vertices are (0,a) and (0,-a)
• So in our present case, the coordinates are: (0,3) and (0,-3)
• This is the answer for part (ii).
5. The length of major axis is 2a
• So in our present case, the length is: 2 × 3 = 6 units
• This is the answer for part (iii).
6. The length of minor axis is 2b
• So in our present case, the length is: 2 × 2 = 4 units
• This is the answer for part (iv).
7. Eccentricity is given by: e = c/a
• So in our present case, e = √5/3
• This is the answer for part (v).
8. We have: Length of latus rectum = $\frac{2 b^2}{a}$
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{\text{Length}}
& {~=~}& {\frac{2 × 2^2}{3}}
&{} \\

{}&{}
& {~=~}& {\frac{8}{3}~\text{= 2.7 units}}
&{} \\

\end{array}$

• This is the answer for part (vi).

9. The actual plot is shown below:

Fig.11.41

Solved example 11.11
Find the equation of the ellipse whose vertices are (±13,0) and foci are (±5,0).
Solution:
1. Given that, vertices are (-13,0) and (13,0)
• Vertices are the end points of the major axis. The given vertices lie on the x-axis.
• So we can write:
The major axis of the given ellipse lies along the x-axis.
2. The given vertices are symmetric about the origin O.
• So we can write:
The center of the given ellipse is at O.
3. Based on the above two steps, we can write:
• Equation of the given ellipse is of the form: $\frac{x^2}{a^2}~+~\frac{y^2}{b^2}~=~1$
4. The vertices are (-13,0) and (13,0).
• So length of the major axis
= Distance between (-13,0) and (13,0)
= 2a = (13 + 13) = 26 
• Thus we get: a = 13 units.
5. Given that, foci are (-5,0) and (5,0).
• So distance of any one focus from center = c = 5 unit.
6. Now we have 'a' and 'c'. We can calculate 'b'.
• We have: c² = a² - b².
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{5^2}
& {~=~}& {13^2~-~b^2}
&{} \\

{\Rightarrow}&{25}
& {~=~}& {169~-~b^2}
&{} \\

{\Rightarrow}&{b^2}
& {~=~}& {169~-~25}
&{} \\

{\Rightarrow}&{b^2}
& {~=~}& {144}
&{} \\

{\Rightarrow}&{b}
& {~=~}& {12}
&{} \\

\end{array}$

• So the value of b is 12 units.

7. Now we have 'a' and 'b'.
• Based on step (3), we can write:
Equation of the ellipse is: $\frac{x^2}{13^2}~+~\frac{y^2}{12^2}~=~1$

Solved example 11.12
Find the equation of the ellipse whose length of the major axis is 20 and foci are (0,±5)
Solution:
1. Given that, foci are (0,5) and (0,-5)
• Both these points lie on the y-axis.
• So we can write:
Major axis of the ellipse lies along the y-axis.
2. The foci (0,5) and (0,-5) are symmetric about the origin O.
• So we can write:
Center of the given ellipse is at O.
3. Based on the above two steps, we can write:
• Equation of the given ellipse is of the form: $\frac{x^2}{b^2}~+~\frac{y^2}{a^2}~=~1$
4. Given that, foci are (0,5) and (0,-5).
• So distance of any one focus from center = c = 5 unit.
5. Given that, length of the major axis is 20 units.
• So we can write:
Length of the semi major axis = a = 10 units.
6. Now we have 'a' and 'c'. We can calculate 'b'.
• We have: c² = a² - b².
• Substituting the known values, we get:

$\begin{array}{ll}
{}&{5^2}
& {~=~}& {10^2~-~b^2}
&{} \\

{\Rightarrow}&{25}
& {~=~}& {100~-~b^2}
&{} \\

{\Rightarrow}&{b^2}
& {~=~}& {100~-~25}
&{} \\

{\Rightarrow}&{b^2}
& {~=~}& {75}
&{} \\

{\Rightarrow}&{b}
& {~=~}& {5 \sqrt{3}}
&{} \\

\end{array}$

• So the value of b is $5 \sqrt{3}$ units.

7. Now we have 'a' and 'b'.
• Based on step (3), we can write:
Equation of the ellipse is: $\frac{x^2}{(5 \sqrt{3})^2}~+~\frac{y^2}{10^2}~=~1$
• Which is same as: $\frac{x^2}{75}~+~\frac{y^2}{100}~=~1$

Solved example 11.13
Find the equation of the ellipse, with major axis along the x-axis and passing through the points (4,3) and (-1,4).
Solution:
1. Given that, major axis lies along the x-axis.
• So the equation of the ellipse will be of the form: $\frac{x^2}{a^2}~+~\frac{y^2}{b^2}~=~1$
2. Since (4,3) ans (-1,4) lie on the ellipse, we can write:
(i) $\frac{4^2}{a^2}~+~\frac{3^2}{b^2}~=~1$
• Which is same as: $\frac{16}{a^2}~+~\frac{9}{b^2}~=~1$
(ii) $\frac{(-1)^2}{a^2}~+~\frac{4^2}{b^2}~=~1$
• Which is same as: $\frac{1}{a^2}~+~\frac{16}{b^2}~=~1$ 
3. Let $\frac{1}{a^2}~=~P~\text{and}~\frac{1}{b^2}~=~Q$
    ♦ Then 2(i) will become: 16P + 9Q = 1
    ♦ Also, 2(ii) will become: P + 16Q = 1
4. Solving the two equations in step (3), we get:
(i) P = $\frac{1}{a^2}~=~\frac{7}{247}$
• So $a^2 ~=~\frac{247}{7}$
(ii) Q = $\frac{1}{b^2}~=~\frac{15}{247}$
• So $b^2 ~=~\frac{247}{15}$
5. Now we have 'a' and 'b'. So based on step (1), we can write:
Equation of the given ellipse is: $\frac{x^2}{247/7}~+~\frac{y^2}{247/15}~=~1$

---

Link to a few more solved examples is given below:

Exercise 11.3

---

In the next section, we will see hyperbola.

Previous

Contents

Next

Copyright©2023 Higher secondary mathematics.blogspot.com