Chapter 10.1 - Slope of a Line

In the previous section, we saw some basic concepts and formulae in coordinate geometry. In this section, we will see slope of lines.

Inclination of a line and Slope of a line

First we will see inclination of a line. It can be written in 4 steps:
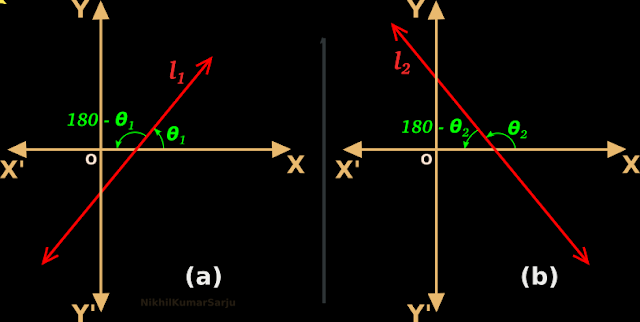
1. In fig.10.5(a) below,
(i) The angle between the line l₁ and the +ve side of the x-axis is 𝜃₁.
(ii) The angle 𝜃₁ is measured from the +ve side of the x-axis in the anti-clockwise direction.
• If the above two conditions are satisfied, then 𝜃₁ is called the inclination of the line l₁.

Fig.10.5

2. Consider the line l₂ in fig.10.5(b) above.
• Based on what we saw in fig.(a), we can write:
Inclination of the line l₂ is  𝜃₂
• This is because, the two conditions are satisfied:
(i) 𝜃₂ is measured from the +ve side of the x-axis.
(ii) 𝜃₂ is measured in the anti-clockwise direction.
3. Based on the two figs. (a) and (b), we can write:
• Inclination of a line parallel to the x-axis will be 0^o
• Inclination of a line parallel to the y-axis will be 90^o
4. So it is obvious that:
    ♦ Inclination of a line can never be less than 0^o.
    ♦ Inclination of a line can never be greater than 180^o.
• We can write: 0^o≤ 𝜃 ≤ 180^o.

---

Now we will see slope of a line. It can be written in steps:
1. We have seen how to write the inclination 𝜃 of any line l
• Now, tan 𝜃 is called the slope of that line l
2. Another name for slope is gradient.
• So we can write in either of the two ways:
    ♦ tan 𝜃 is the slope of the line l
    ♦ tan 𝜃 is the gradient of the line l
3. Slope of a line whose inclination is zero (a horizontal line) = tan 0 = 0
4. Slope of a line whose inclination is 90^o (a vertical line) = tan 90
    ♦ But tan 90 gives a number which does not exist.
    ♦ So slope of such a line is not defined
5. Based on this, we can write:
    ♦ Slope of x-axis = 0
    ♦ Slope of y-axis is not defined.

---

Slope from coordinates

• We know that, a line can be completely determined if we know the coordinates of any two points on it.
• If we know those coordinates, we can find the slope also. Let us see how it is done. It can be written in 7 steps:
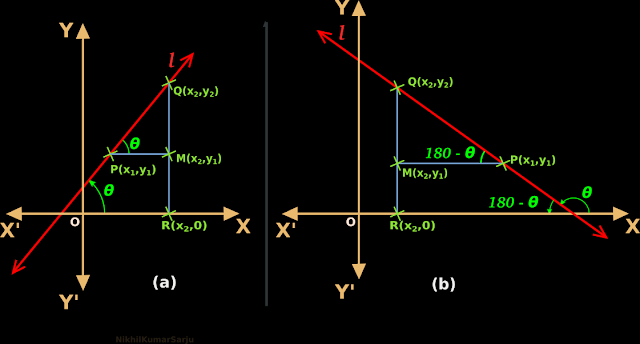
1. In fig.10.6(a) below, the non-vertical line l has an inclination of 𝜃
• P (x₁, y₁) and Q (x₂,y₂) are two points on the line.

Fig.10.6

• Note:
In fig.10.6(a), x₁ cannot be equal to x₂. If they are equal, line l will become vertical. The slope of a vertical line is not defined.
2. A line QR is drawn perpendicular to the x-axis.
• Another line PM is drawn perpendicular to QR.
3. In the triangle PMQ, angle QPM will be equal to 𝜃.
So we can write:
$\text{Slope of}~l~=~\tan \theta ~=~\frac{QM}{PM}$
4. Now, the coordinates of M will be (x₂,y₁)
So the distance QM wil be (y₂ – y₁)
5. Since the coordinates of M are (x₂,y₁), the distance PM will be (x₂ – x₁)
6. Based on steps (3), (4) and (5), we get:
$\text{Slope of}~l~=~\tan \theta ~=~\frac{QM}{PM}~=~\frac{y_2 - y_1}{x_2 - x_1}$
7. Thus we get a simple method to find the slope using coordinates.

---

In the fig.10.6(a) above, the inclination 𝜃 is an acute angle. Let us see the case when 𝜃 is an obtuse angle. It can be written in steps:
1. In fig.10.6(b) above, the non-vertical line l has an inclination of 𝜃
• P (x₁, y₁) and Q (x₂,y₂) are two points on the line.
• Note:
In fig.10.6(b), x₁ cannot be equal to x₂. If they are equal, line l will become vertical. The slope of a vertical line is not defined.
2. A line QR is drawn perpendicular to the x-axis.
• Another line PM is drawn perpendicular to QR.
3. In the triangle PMQ, angle QPM will be equal to (180 - 𝜃).
So we can write:
$\text{Slope of}~l~=~\tan (180~-~\theta) ~=~-\tan \theta~=~\frac{QM}{PM}$
[See identities 9(c) and 9(d) in the list of identities]
4. Now, the coordinates of M will be (x₂,y₁)
So the distance QM wil be (y₂ – y₁)
5. Since the coordinates of M are (x₂,y₁), the distance PM will be (x₁ – x₂)
• Note that, in this case, we subtract x₂ from x₁ because, x₁ is larger than x₂.
6. Based on steps (3), (4) and (5), we get:
$\text{Slope of}~l~=~\tan (180~-~\theta) ~=~-\tan \theta~=~\frac{QM}{PM}~=~\frac{y_2 - y_1}{x_1 - x_2}$
• The -ve sign can be avoided by rearranging the denominator. We get:
$\text{Slope of}~l~=~\tan \theta~=~\frac{y_2 - y_1}{x_2 - x_1}$
7. Thus here also, we get the same simple method to find the slope using coordinates.

---

• If a line is horizontal, all points on that line will have the same y coordinates.
    ♦ That is., y₂ will be equal to y₁.
• Then the numerator will become zero.
• Consequently, tan 𝜃 will become zero.
• So the above result is applicable to all non-vertical lines, even if the line is horizontal.
• We can write:
If P (x₁, y₁) and Q (x₂,y₂) are two points on a non-vertical line, then the slope of that line will be equal to $\frac{y_2 - y_1}{x_2 - x_1}$
• Note that, in the numerator, we have a distance. Distance can be measured in meter or centimeter. In the denominator also, we have distance. So the units will cancel each other. That means: Slope has no units. It is just a number.

---

Condition for parallelism

This can be written in steps:
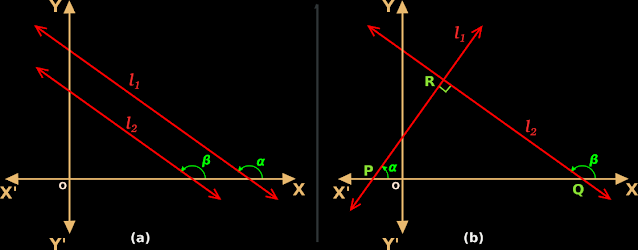
1. Fig.10.7(a) below shows two non-vertical lines l₁ and l₂.
    ♦ l₁ has an inclination of 𝛼
    ♦ l₂ has an inclination of β
    ♦ The slope of l₁ is m₁
    ♦ The slope of l₂ is m₂

Fig.10.7

2. From our earlier geometry classes, we know this:
    ♦ If l₁ and l₂ are parallel, then 𝛼 = β
3. But if 𝛼 = β, then tan 𝛼 = tan β
    ♦ If tan 𝛼 = tan β, then m₁ = m₂
• So the condition for two lines l₁ and l₂ to be parallel is:
Their slopes m₁ and m₂ must be equal.

---

Let us prove the converse.
• We need to prove that, if slopes m₁ and m₂ of the two lines l₁ and l₂ are equal, then the two lines are parallel.
It can be proved in 5 steps:
1. Given that, m₁ = m₂
Then we can write: tan 𝛼 = tan β
2. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
3. So, if tan 𝛼 = tan β, we can write:
𝛼 = n𝞹 + β
• Let us put the smallest possible value of 'n', which is 1
We get: 𝛼 = 𝞹 + β
4. But (𝞹 + β) is greater than 180^o
• Inclination cannot be greater than 180^o
• So the only possibility is that 𝛼 = β.
If 𝛼 = β, then the two lines are parallel
5. Thus we arrive at the conclusion:
If slopes m₁ and m₂ of two lines are equal, then the lines will be parallel.

---

Condition for perpendicularity

This can be written in 3 steps:
1. Fig.10.7(b) above shows two non-vertical lines l₁ and l₂.
    ♦ l₁ has an inclination of 𝛼
    ♦ l₂ has an inclination of β
    ♦ The slope of l₁ is m₁
    ♦ The slope of l₂ is m₂
2. Formation of triangle PQR:
    ♦ l₁ and l₂ intersect at R.
    ♦ l₁ intersect the x-axis at P
    ♦ l₂ intersect the x-axis at q
• Thus we get a right angled triangle PQR
3. Relation between 𝛼 and β:
• β is an exterior angle of the triangle PQR
• For this exterior angle β, the angles 𝛼 and 90^o are remote interior angles.
• So we get: β = 𝛼 + 90
• This result can be used to find a relation between the two slopes:

$\begin{array}{ll}
{}&{\beta}
&{}={}& {\alpha + 90^o}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \beta}
&{}={}& {\tan (\alpha + 90^o)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \beta}
&{}={}& {- \cot \alpha}
&{\color {green}{\text{- - - (a) }}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \beta}
&{}={}& {- \frac{1}{\tan \alpha}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{m_2}
&{}={}& {- \frac{1}{m_1}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{m_1 m_2}
&{}={}& {- 1}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
• Line marked as (a):
See identities 9(a) and 9(b) in the list of identities.
tan (90+𝜃) = -cot 𝜃
• So the condition for two lines l₁ and l₂ to be perpendicular is:
Product of their slopes (m₁ m₂) must be -1.

---

Let us prove the converse.
• We need to prove that, if product of the slopes (m₁ m₂) of the two lines l₁ and l₂ is -1, then the two lines are perpendicular to each other.
It can be proved in 3 steps:

1. Relation between 𝛼 and β:

$\begin{array}{ll}
{}&{m_1 m_2}
&{}={}& {-1}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \alpha × \tan \beta}
&{}={}& {-1}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \alpha}
&{}={}& {- \frac{1}{ \tan \beta}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \alpha}
&{}={}& {- \cot \beta}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \alpha}
&{}={}& {\tan (90^o + \beta)}
&{\color {green}{\text{- - - (a) }}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\alpha}
&{}={}& {90^o + \beta}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
• Line marked as (a):
See identities 9(a) and 9(b) in the list of identities.
tan (90+𝜃) = -cot 𝜃

2. So 𝛼 and β differ by 90^o
• Then based on fig.10.7(b), the two lines will be perpendicular to each other.
3. So it is clear that, if (m₁m₂) = -1, then the two lines are perpendicular to each other.

Let us see a solved example

Solved example 10.1
Find the slope of the following lines:
(a) Line passing through the points (3,-2) and (-1,4)
(b) Line passing through the points (3,-2) and (7,-2)
(c) Line passing through the points (3,-2) and (3,4)
(d) Line making an inclination of 60^o with the positive direction of the x-axis.
Solution:
If a line pass through two points (x₁,y₁) and (x₂,y₂), then the slope of that line will be $\frac{y_2 - y_1}{x_2 - x_1}$ 
Part (a): Slope = $\frac{4 - -2}{-1 - 3}~=~\frac{6}{-4}~=~-\frac{3}{2}$
Part (b): Slope = $\frac{-2 - -2}{7 - 3}~=~\frac{0}{4}~=~0$
Part (c): Slope = $\frac{4 - -2}{3 - 3}~=~\frac{6}{0},~\text{which is not defined}$
Part (d): Slope is the tangent of inclination. So we get:
Slope = tan 60^o = $\sqrt{3}$

---

In the next section, we will see angle between two lines.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com