Chapter 10.9 - Distance of a Point from a Line

In the previous section, we saw the details about normal form. In this section, we will see distance of a point from a line. Later in this section we will see distance between two parallel lines also.

• We can derive an expression for the distance in 9 steps:
1. In fig.10.38 below, equation of line L is Ax + By + C = 0

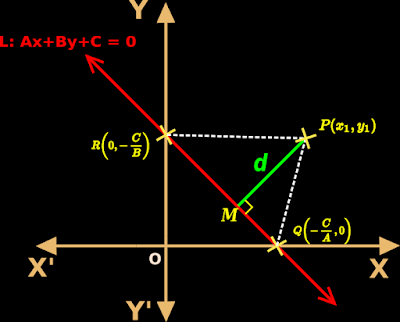Fig.10.38

2. This line intersects the x-axis at Q.
• We know that, the x-intercept will be $-\frac{C}{A}$. So the coordinates of Q will be: $\left(-\frac{C}{A},0 \right)$
3. This line intersects the y-axis at R.
• We know that, the y-intercept will be $-\frac{C}{B}$. So the coordinates of R will be $\left(0,-\frac{C}{B} \right)$
4. P(x₁,y₁) is a point on the xy-plane.
• A perpendicular is dropped from P onto the line L
    ♦ Foot of the perpendicular is M.
    ♦ The length of the line segment PM is d.
    ♦ d is called the distance of the point P from line L.
5. It is possible to draw infinite lines from P onto line L.
• But it is possible to draw only one perpendicular.
• The length of that perpendicular line is called the distance of the point from L.
• The other lengths are not eligible to be considered as the distance of the point from L.
6. Our aim is to derive an expression for d
• Consider the triangle PQR. We have the coordinates of all three vertices:
$P(x_1,y_1),~Q\left(-\frac{C}{A},0 \right),~R\left(0,-\frac{C}{B} \right)$
• So we can find the area of that triangle. We get:

$\begin{array}{ll}
{}&{Area}
&{}={}& {\frac{1}{2}\left|x_1(y_2 - y_3)~+~x_2(y_3 - y_1)~+~x_3(y_1 - y_2) \right|}
&{} \\

{}&{}
&{}={}& {\frac{1}{2}\left|x_1 \left(0~-~-\frac{C}{B}\right)~+~-\frac{C}{A} × \left(-\frac{C}{B}~-~y_1 \right)~+~0 × \left(y_1~-~0\right) \right|}
&{} \\

{}&{}
&{}={}& {\frac{1}{2}\left|\frac{C x_1}{B}~+~\frac{C^2}{AB}~+~\frac{C y_1}{A} \right|}
&{} \\

{}&{}
&{}={}& {\frac{1}{2}\left| \frac{C}{AB}\left(\frac{C x_1}{B} × \frac{AB}{C}~+~\frac{C^2}{AB} × \frac{AB}{C}~+~\frac{C y_1}{A} × \frac{AB}{C}\right) \right|}
&{\color{green}{\text{- - - (a)}}} \\

{}&{}
&{}={}& {\frac{1}{2}\left| \frac{C}{AB}\left(\frac{x_1}{1} × \frac{A}{1}~+~C~+~\frac{y_1}{1} × \frac{B}{1}\right) \right|}
&{} \\

{}&{}
&{}={}& {\frac{1}{2}\left| \frac{C}{AB}\left(A x_1~+~B y_1~+~C\right) \right|}
&{} \\

{}&{}
&{}={}& {\frac{1}{2} × \left| \frac{C}{AB}\right| × \left|\left(A x_1~+~B y_1~+~C\right) \right|}
&{} \\

\end{array}$

◼ Remarks:
Line marked as (a):
In this line, we multiply each term by $\frac{C}{AB}$ and $\frac{AB}{C}$.

7. We know that, area of any triangle = 1/2 × Base × Altitude
• In our present case,
    ♦ Base of triangle PQR is QR
    ♦ Altitude of triangle PQR is d
• We know the coordinates of both Q and R:
$Q\left(-\frac{C}{A},0 \right),~R\left(0,-\frac{C}{B} \right)$
• So the length QR can be obtained as:

$\begin{array}{ll}
{}&{QR}
&{}={}& {\sqrt{(x_2 - x_1)^2~+~(y_2 - y_1)^2}}
&{} \\

{}&{}
&{}={}& {\sqrt{\left(0~-~ -\frac{C}{A}\right)^2~+~\left(-\frac{C}{B} - 0 \right)^2}}
&{} \\

{}&{}
&{}={}& {\sqrt{\frac{C^2}{A^2}~+~\frac{C^2}{B^2}}}
&{} \\

{}&{}
&{}={}& {\sqrt{ \frac{C^2}{A^2 B^2} \left(\frac{C^2}{A^2} × \frac{A^2 B^2}{C^2}~+~\frac{C^2}{B^2} × \frac{A^2 B^2}{C^2}\right)}}
&{\color{green}{\text{- - - (a)}}} \\

{}&{}
&{}={}& {\sqrt{ \frac{C^2}{A^2 B^2} \left(B^2~+~A^2\right)}}
&{} \\

{}&{}
&{}={}& {\sqrt{ \frac{C^2}{A^2 B^2}} × \sqrt{\left(B^2~+~A^2\right)}}
&{} \\

{}&{}
&{}={}& {\left| \frac{C}{AB} \right| × \sqrt{\left(A^2~+~B^2\right)}}
&{} \\

\end{array}$

◼ Remarks:
Line marked as (a):
In this line, we multiply each term by $\frac{C^2}{A^2 B^2}$ and $\frac{A^2 B^2}{C^2}$.

• Now we can obtain the area of the triangle PQR:

$\begin{array}{ll}
{}&{Area}
&{}={}& {\frac{1}{2} × \text{Base} × \text{Altitude}}
&{} \\

{}&{}
&{}={}& {\frac{1}{2} × QR ×d}
&{} \\

{}&{}
&{}={}& {\frac{1}{2} × \left| \frac{C}{AB} \right| × \sqrt{\left(A^2~+~B^2\right)} × d}
&{} \\

\end{array}$

8. Equating the areas:
    ♦ In (6), we obtained the area of triangle PQR.
    ♦ In (7) also, we obtained the area of triangle PQR.
• We can equate the two areas:

$\begin{array}{ll}
{}&{\frac{1}{2} × \left| \frac{C}{AB}\right| × \left|\left(A x_1~+~B y_1~+~C\right) \right|}
&{}={}& {\frac{1}{2} × \left| \frac{C}{AB} \right| × \sqrt{\left(A^2~+~B^2\right)} × d}
&{} \\

{\Rightarrow}&{\left|\left(A x_1~+~B y_1~+~C\right) \right|}
&{}={}& {\sqrt{\left(A^2~+~B^2\right)} × d}
&{} \\

{\Rightarrow}&{d}
&{}={}& {\frac{\left|\left(A x_1~+~B y_1~+~C\right) \right|}{\sqrt{\left(A^2~+~B^2\right)}}}
&{} \\

\end{array}$

9. Thus we get a formula to find the distance.
$d~=~\frac{\left|A x_1~+~B y_1~+~C \right|}{\sqrt{A^2~+~B^2}}$

---

Distance between two parallel lines

• We have derived a formula for the distance of a point from a line. Using this formula, we can derive another formula for the distance between two parallel lines. It can be derived in 5 steps:
1. In fig.10.39 below,
    ♦ equation of line L₁ is A₁x + B₁y + C₁ = 0
    ♦ equation of line L₂ is A₂x + B₂y + C₂ = 0

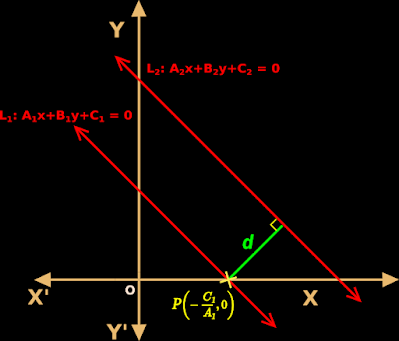Fig.10.39

2. Line L₁ intersects the x-axis at P
• Then the coordinates of P will be $\left(-\frac{C_1}{A_1},0 \right)$
3. A perpendicular line is dropped from P onto the line L₂
• Length of this perpendicular line is d
• Then we can write:
The distance between the two parallel lines is d.
4. We can use the formula derived earlier to find d.
• For applying the formula, we take P as the point and L₂ as the line. Thus we get:

$\begin{array}{ll}
{}&{d}
&{}={}& {\frac{\left|A x_1~+~B y_1~+~C \right|}{\sqrt{A^2~+~B^2}}}
&{} \\

{}&{}
&{}={}& {\frac{\left|A_2 × -\frac{C_1}{A_1}~+~B_2  × 0~+~C_2 \right|}{\sqrt{A_2^2~+~B_2^2}}}
&{} \\

{}&{}
&{}={}& {\frac{\left|A_2 × -\frac{C_1}{A_1}~+~C_2 \right|}{\sqrt{A_2^2~+~B_2^2}}}
&{} \\

{}&{}
&{}={}& {\frac{\left| \frac{-A_2 C_1~+~A_1 C_2}{A_1}\right|}{\sqrt{A_2^2~+~B_2^2}}}
&{} \\

{}&{}
&{}={}& {\frac{\left| \frac{A_1 C_2~-~A_2 C_1}{A_1}\right|}{\sqrt{A_2^2~+~B_2^2}}}
&{} \\

{}&{}
&{}={}& {\frac{\frac{\left|A_1 C_2~-~A_2 C_1 \right|}{\left|A_1\right|}}{\sqrt{A_2^2~+~B_2^2}}}
&{} \\

{}&{}
&{}={}& {\frac{\left|A_1 C_2~-~A_2 C_1 \right|}{\left|A_1\right| × \sqrt{A_2^2~+~B_2^2}}}
&{} \\

\end{array}$

5. Thus we get a formula to find the distance between two parallel lines.
$d~=~\frac{\left|A_1 C_2~-~A_2 C_1 \right|}{\left|A_1\right| × \sqrt{A_2^2~+~B_2^2}}$

---

Now we will see two solved examples

Solved example 10.18
Find the distance of the point (3,-5) from the line 3x - 4y - 26 = 0
Solution:
1. The given line is: 3x - 4y - 26 = 0
• So we get: A = 3, B = -4 and C = -26
2. We have: $d~=~\frac{\left|A x_1~+~B y_1~+~C \right|}{\sqrt{A^2~+~B^2}}$

• Substituting the known values, we get:

$\begin{array}{ll}
{}&{d}
&{}={}& {\frac{\left|3 × 3~+~-4 × -5~+~-26 \right|}{\sqrt{3^2~+~(-4)^2}}}
&{} \\

{}&{}
&{}={}& {\frac{\left|9~+~20~+~-26 \right|}{\sqrt{9~+~16}}}
&{} \\

{}&{}
&{}={}& {\frac{\left|3 \right|}{\sqrt{25}}}
&{} \\

{}&{}
&{}={}& {\frac{3}{5}~=~0.6~\text{units}}
&{} \\

\end{array}$

3. The actual plot is shown below:

Fig.10.40

 

Solved example 10.19
Find the distance between the parallel lines 3x - 4y + 7 = 0 and 3x - 4y + 5 = 0
Solution:
1. Let the line L₁ be: 3x - 4y + 7 = 0
• Then we get: A₁ = 3, B₁ = -4 and C₁ = 7
2. Let the line L₂ be: 3x - 4y + 5 = 0
• Then we get: A₂ = 3, B₂ = -4 and C₂ = 5
3. We have: $d~=~\frac{\left|A_1 C_2~-~A_2 C_1 \right|}{\left|A_1\right| × \sqrt{A_2^2~+~B_2^2}}$

• Substituting the known values, we get:

$\begin{array}{ll}
{}&{d}
&{}={}& {\frac{\left|3 × 5~-~3 × 7 \right|}{\left|3 \right| × \sqrt{3^2~+~(-4)^2}}}
&{} \\

{}&{}
&{}={}& {\frac{\left|15~-~21 \right|}{\left|3 \right| × \sqrt{9~+~16}}}
&{} \\

{}&{}
&{}={}& {\frac{\left|-6 \right|}{\left|3 \right| × 5}}
&{} \\

{}&{}
&{}={}& {\frac{6}{3× 5}}
&{} \\

{}&{}
&{}={}& {\frac{2}{5}~=~0.4~\text{units}}
&{} \\

\end{array}$

4. The actual plot is shown below:

Fig.10.41

---

Link to a few more solved examples is given below:

Exercise 10.3

---

In the next section, we will see some miscellaneous examples.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com