Chapter 10.5 - Intercept Form

In the previous section, we saw some of the different forms of the equation of a line. In this section, we will see intercept form.

Intercept form

• Suppose that, we are given the following two items:
   ♦ x-intercept of a line.
   ♦ y-intercept of that line.
• Then we can quickly write the equation of that line. Let us see how it is done.

Case I
This can be written in 4 steps:
1. Let the x-intercept be 'a'.
• Then the point of intersection of the line with the x-axis will be (a,0).
    ♦ This is shown in fig.10.26(a) below:

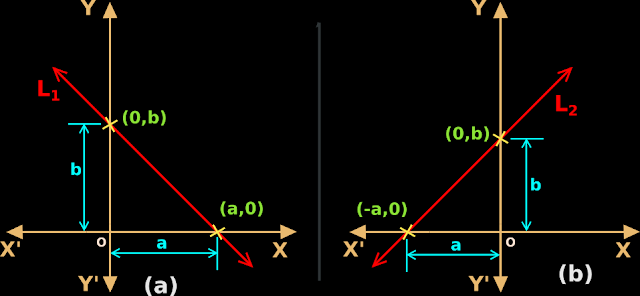Fig.10.26

2. Let the y-intercept be 'b'.
• Then the point of intersection of the line with the y-axis will be (0,b)
3. Now we have two points on the line. They are: (a,0) and (0,b).
• So we can use the two-point form: $y-y_1~=~\frac{y_2-y_1}{x_2-x_1} (x-x_1)$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{y-0}
&{}={}& {\frac{b-0}{0-a} (x-a)}
&{} \\

{\Rightarrow}&{y-0}
&{}={}& {\frac{-b}{a} (x-a)}
&{} \\

{\Rightarrow}&{ya}
&{}={}& {-bx+ab}
&{} \\

{\Rightarrow}&{\frac{y}{b}}
&{}={}& {\frac{-x}{a}~+~1}
&{\color{green}{\text{- - - (a)}}} \\

{\Rightarrow}&{\frac{x}{a} + \frac{y}{b}}
&{}={}& {1}
&{} \\

\end{array}$

◼ Remarks:
• Line marked as (a):
In this line, we divide both sides by ab
4. So we get an equation: $\frac{x}{a} + \frac{y}{b} = 1$
 

Case II
This can be written in 4 steps:
1. In case I, we derived an equation based on fig.10.26(a) above.
• In this fig.,
    ♦ the line intersects the x-axis at the +ve side.
    ♦ the line intersects the y-axis also at the +ve side.
2. What if
    ♦ the line intersect the x-axis at the -ve side.
    ♦ the line intersect the y-axis at the +ve side.
• Such a situation is shown in fig.10.26(b) above.
3. But this situation should not discourage us. Because, we have the two points where the line cuts the x-axis and y-axis. The points are (-a,0) and (0,b).
• Using the two-point form as before, we get:
$\begin{array}{ll}
{}&{y-0}
&{}={}& {\frac{b-0}{0-~-a} (x-~-a)}
&{} \\

{\Rightarrow}&{y-0}
&{}={}& {\frac{b}{a} (x+a)}
&{} \\

{\Rightarrow}&{ya}
&{}={}& {bx+ab}
&{} \\

{\Rightarrow}&{\frac{y}{b}}
&{}={}& {\frac{x}{a}~+~1}
&{} \\

{\Rightarrow}&{\frac{-x}{a} + \frac{y}{b}}
&{}={}& {1}
&{} \\

{\Rightarrow}&{\frac{x}{-a} + \frac{y}{b}}
&{}={}& {1}
&{} \\

\end{array}$

4. This is similar to the equation that we derived in case I. The 'a' has become '-a' because, the x-intercept in this case is -ve.

Case III
This can be written in 2 steps:
1. A third possible situation is shown in fig.10.27(a) below:

Fig.10.27

• Here the points are: (a,0) and (0,-b). Proceeding as before, we get:

$\begin{array}{ll}
{}&{y-0}
&{}={}& {\frac{-b-0}{0-a} (x-a)}
&{} \\

{\Rightarrow}&{y-0}
&{}={}& {\frac{-b}{-a} (x-a)}
&{} \\

{\Rightarrow}&{y-0}
&{}={}& {\frac{b}{a} (x-a)}
&{} \\

{\Rightarrow}&{ya}
&{}={}& {bx-ab}
&{} \\

{\Rightarrow}&{\frac{y}{b}}
&{}={}& {\frac{x}{a}~-~1}
&{} \\

{\Rightarrow}&{\frac{x}{a} - \frac{y}{b}}
&{}={}& {1}
&{} \\

{\Rightarrow}&{\frac{x}{a} + \frac{y}{-b}}
&{}={}& {1}
&{} \\

\end{array}$

2. This is similar to the equation that we derived in case I. The 'b' has become '-b' because, the y-intercept in this case is -ve.  

Case IV
This can be written in 2 steps:
1. The fourth and last possible situation is shown in fig.10.27(b) above.

• Here the points are: (-a,0) and (0,-b). Proceeding as before, we get:

$\begin{array}{ll}
{}&{y-0}
&{}={}& {\frac{-b-0}{0-~-a} (x-~-a)}
&{} \\

{\Rightarrow}&{y-0}
&{}={}& {\frac{-b}{a} (x+a)}
&{} \\

{\Rightarrow}&{ya}
&{}={}& {-bx-ab}
&{} \\

{\Rightarrow}&{\frac{y}{b}}
&{}={}& {\frac{-x}{a}~-~1}
&{} \\

{\Rightarrow}&{\frac{x}{a} + \frac{y}{b}}
&{}={}& {-1}
&{} \\

{\Rightarrow}&{\frac{x}{-a} + \frac{y}{-b}}
&{}={}& {1}
&{} \\

\end{array}$

2. This is similar to the equation that we derived in case I.
    ♦ The 'a' has become '-a' because, the x-intercept in this case is -ve. 
    ♦ The 'b' has become '-b' because, the y-intercept in this case is -ve. 

---

Based on the four cases, we can write:
• In the intercept form, we can use the general equation: $\frac{x}{a} + \frac{y}{b} = 1$
• But care must be taken regarding the signs of 'a' and 'b'.
(This equation is easy to remember because, x is divided by the x-intercept. Similarly, y is divided by the y-intercept)

---

• Fig.10.28 below shows the actual plot of four lines.

1. Equation of the red line L₁ is: $\frac{x}{-3} + \frac{y}{4} = 1$
• We see that:
    ♦ L₁ cuts the x-axis at (-3,0) 
    ♦ L₁ cuts the y-axis at (0,4)

Fig.10.28

 

2. Equation of the green line L₂ is: $\frac{x}{-6} + \frac{y}{-4} = 1$
• We see that:
    ♦ L₂ cuts the x-axis at (-6,0) 
    ♦ L₂ cuts the y-axis at (0,-4)

3. Equation of the magenta line L₃ is: $\frac{x}{3} + \frac{y}{5} = 1$
• We see that:
    ♦ L₃ cuts the x-axis at (3,0) 
    ♦ L₃ cuts the y-axis at (0,5)      

4. Equation of the pink line L₄ is: $\frac{x}{6} + \frac{y}{-3} = 1$
• We see that:
    ♦ L₄ cuts the x-axis at (6,0) 
    ♦ L₄ cuts the y-axis at (0,-3)

---

In the next section, we will see normal form.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com