Chapter 10.4 - Various Forms of Equations of A Line

In the previous section, we saw collinearity of three points. In this section, we will see the various forms of the equation of a line.

Some basics can be written in 3 steps:
1. Consider a line L lying in the xy-plane.
• We know that in any line, there will be infinite number of points.
• But there are other infinite points which do not lie on the line.
2. Then what is the difference between the following two types of points:
(i) Points which lie on L
(ii) Points which do not lie on L  
• The answer is:
   ♦ All points lying on L, will satisfy a particular condition.
   ♦ The points which do not lie on L, will not satisfy that condition.
3. We can write this is another way also:
Take any point on the xy-plane. If that point satisfies a particular condition, then that point will lie on L.

---

• So our next aim is to find the conditions for different types of lines.
• First we will see horizontal lines.

Equation of a horizontal line

This can be written in 9 steps.
1. The red line L₁ in fig.10.16(a) is parallel to the x-axis.
   ♦ It is a horizontal line.
   ♦ It is at a distance of ‘a’ from the x-axis.

Fig.10.16

2. Consider any point on L₁. The ordinate (y-coordinate) of that point will be 'a'.
• Conversely, any point whose ordinate is a, will lie on L₁
3. So we can write:
The condition for a point to lie on L₁ is that, the ordinate of that point must be ‘a’
4. In algebraic form, we can write: y = a
• This algebraic form is the equation of line L₁
• We can write:
Equation of L₁ is: y = a
5. Now consider the red line L₁' in fig.10.16(b) above.
   ♦ It is parallel to the x-axis
   ♦ It is a horizontal line.
   ♦ It is at a distance of ‘a’ from the x-axis.
6. Consider any point on L₁'. The ordinate (y-coordinate) of that point will be '-a'.
• Conversely, any point whose ordinate is -a, will lie on L₁'
7. So we can write:
The condition for a point to lie on L₁' is that, the ordinate of that point must be ‘-a’
8. In algebraic form, we can write: y = -a
• This algebraic form is the equation of line L₁'
• We can write:
Equation of L₁' is: y = -a
9. In general, we can write:
Equation of any horizontal line will be in the form: $y=\pm a$
   ♦ Where ‘a’ is a constant.
         ✰ We use the ‘+’ sign when the horizontal line is above the x-axis.
         ✰ We use the ‘-’ sign when the horizontal line is below the x-axis.

Equation of a vertical line

This can be written in 9 steps.
1. The red line L₂ in fig.10.17(a) is parallel to the y-axis.
   ♦ It is a vertical line.
   ♦ It is at a distance of ‘b’ from the y-axis.

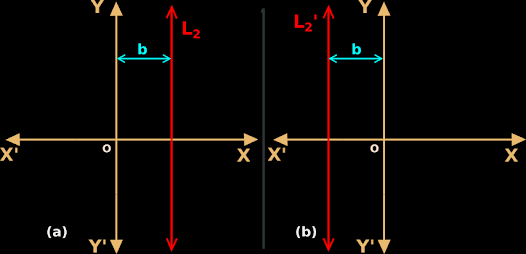Fig.10.17

2. Consider any point on L₂. The abscissa (x-coordinate) of that point will be 'b'.
• Conversely, any point whose abscissa is 'b', will lie on L₂
3. So we can write:
The condition for a point to lie on L₂ is that, the abscissa of that point must be ‘b’
4. In algebraic form, we can write: x = b
• This algebraic form is the equation of line L₂
• We can write:
Equation of L₂ is: x = b
5. Now consider the red line L₂' in fig.10.17(b) above.
   ♦ It is parallel to the y-axis
   ♦ It is a vertical line.
   ♦ It is at a distance of ‘b’ from the y-axis.
6. Consider any point on L₂'. The abscissa (x-coordinate) of that point will be '-b'.
• Conversely, any point whose abscissa is -b, will lie on L₂'
7. So we can write:
The condition for a point to lie on L₂' is that, the abscissa of that point must be ‘-b’
8. In algebraic form, we can write: x = -b
• This algebraic form is the equation of line L₂'
• We can write:
Equation of L₂' is: x = -b
9. In general, we can write:
Equation of any vertical line will be in the form: $x=\pm b$
   ♦ Where ‘b’ is a constant.
         ✰ We use the ‘+’ sign when the vertical line is on the right side of the y-axis.
         ✰ We use the ‘-’ sign when the vertical line is on the left side of the y-axis.

Solved Example 10.8
Write the equation of the line parallel to x-axis and passing through (-2,3). Also write the equation of the line parallel to y-axis and passing through the same point.
Solution:
1. First we will consider the line parallel to the x-axis.
• It's equation will be of the form $y = \pm a$
• This line passes through (-2,3). So it's distance from the x-axis is 3 units.
   ♦ That means, a = 3
• Also, (-2,3) is above the x-axis.
   ♦ So we use the +ve sign
• So the required equation is: $y = 3$
2. Next we will consider the line parallel to the y-axis.
• It's equation will be of the form $x = \pm b$
• This line passes through (-2,3). So it's distance from the y-axis is 2 units.
   ♦ That means, a = 2
• Also, (-2,3) is on the left side of the y-axis.
   ♦ So we use the -ve sign
• So the required equation is: $x = -2$
3. The actual lines are shown in the fig.10.18 below:

Fig.10.18

• In the above fig,
   ♦ The red line is the required line parallel to the x-axis.
   ♦ The green line is the required line parallel to the y-axis.

---

Point-slope form

• Suppose that, we are given the following two items:
   ♦ Slope of a line.
   ♦ A point through which the line passes.
• Then we can quickly write the equation of that line. Let us see how it is done. It can be written in 7 steps:
1. Let the slope of the line be m
2. Let the line pass through a known point P₀ (x₀,y₀)
• By saying "Known point", we mean that, the values of x₀ and y₀ are known.
3. Let P(x,y) be any point on the line.
4. Now we have two points on the line. They are: P₀(x₀,y₀) and P(x,y). This is shown in fig.10.19 below:

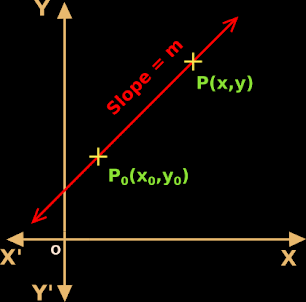Fig.10.19

5. If we have two points on a line, we can write the slope of the line.
• So in our present case, the slope will be $\frac{y-y_0}{x-x_0}$
6. But we are already given the slope. It is m. So we can write:

$\begin{array}{ll}
{}&{m}
&{}={}& {\frac{y-y_0}{x-x_0}}
&{} \\

{\Rightarrow}&{y-y_0}
&{}={}& {m(x-x_0)}
&{} \\
\end{array}$

7. So we get an equation: y-y₀ = m(x-x₀)
• We derived this equation by assuming that, the point (x,y) lies on the line (see fig.10.19).
• That means,
   ♦ if we take any point outside the line, this equation will not be satisfied.
   ♦ if we take any point on the line, this equation will be satisfied.
• So we can say that, y-y₀ = m(x-x₀) is the equation of the line.
   ♦ This is the equation of a line written in slope-point form.
         ✰ The slope is m.
         ✰ The point is (x₀,y₀).

---

Let us see a solved example:
Solved example 10.9
Three lines L₁, L₂ and L₃ pass through the point (-3,4). Write the equation of each of those lines, if their slopes are -3, 2 and 4 respectively. 
Solution:
• Given that,
   ♦ (x₀,y₀) = (-3,4)
   ♦ m₁ = -3
   ♦ m₂ = 2
   ♦ m₃ = 4
• We have the slope-point form: y-y₀ = m(x-x₀)
1. So for L₁, the equation will be:
$\begin{array}{ll}
{}&{y-4}
&{}={}& {-3(x-~-3)}
&{} \\

{\Rightarrow}&{y-4}
&{}={}& {-3x-9}
&{} \\

{\Rightarrow}&{3x + y +5}
&{}={}& {0}
&{} \\
\end{array}$

2. Similarly for L₂, the equation will be:
$\begin{array}{ll}
{}&{y-4}
&{}={}& {2(x-~-3)}
&{} \\

{\Rightarrow}&{y-4}
&{}={}& {2x+6}
&{} \\

{\Rightarrow}&{2x - y +10}
&{}={}& {0}
&{} \\
\end{array}$

3. Finally for L₃, the equation will be:
$\begin{array}{ll}
{}&{y-4}
&{}={}& {4(x-~-3)}
&{} \\

{\Rightarrow}&{y-4}
&{}={}& {4x+12}
&{} \\

{\Rightarrow}&{4x - y +16}
&{}={}& {0}
&{} \\
\end{array}$

4. The actual plot of the three lines are shown in fig.10.20 below:

Fig.10.20

5. We can infer some general information from the plot. They can be written in 3 steps:
(i) If the slope of a line is +ve, that line will have an upward slope. That means, when we move along the x-axis towards the +ve side, the line will be sloping upwards.
   ♦ Lines L₂ and L₃ are examples.
(ii) If the slope of a line is -ve, that line will have a downward slope. That means, when we move along the x-axis towards the +ve side, the line will be sloping downwards.
   ♦ Line L₁ is an example.
(iii) Compare the slopes of two lines.
   ♦ The line with the greater slope will be steeper.
   ♦ The line with the lesser slope will be flatter.
• This will become clear when we compare L₂ and L₃.

---

Two-point form

• Suppose that, we are given two known points on a line.
• Then we can quickly write the equation of that line. Let us see how it is done. It can be written in 6 steps:
1. Let the line pass through two known points P₁ (x₁,y₁) and P₂ (x₂,y₂)
• By saying "Known points", we mean that, the values of x₁, y₁, x₂ and y₂ are known.
2. Let P(x,y) be any point on the line.
3. Now we have three points on the line. They are: P₁(x₁,y₁), P₂(x₂,y₂) and P(x,y). This is shown in fig.10.21 below:

Fig.10.21

4. If there are three points, we can write slopes.
• So in our present case,
   ♦ the slope of line P₁P will be $\frac{y-y_1}{x-x_1}$
   ♦ the slope of line P₁P₂ will be $\frac{y_2-y_1}{x_2-x_1}$
5. But since the three points are collinear, the slopes will be equal. So we can write:

$\begin{array}{ll}
{}&{\frac{y-y_1}{x-x_1}}
&{}={}& {\frac{y_2-y_1}{x_2-x_1}}
&{} \\

{\Rightarrow}&{y-y_1}
&{}={}& {\frac{y_2-y_1}{x_2-x_1} (x-x_0)}
&{} \\
\end{array}$

6. So we get an equation: $y-y_1~=~\frac{y_2-y_1}{x_2-x_1} (x-x_1)$
• We derived this equation by assuming that, the point (x,y) lies on the line (see fig.10.21).
• That means,
   ♦ if we take any point outside the line, this equation will not be satisfied.
   ♦ if we take any point on the line, this equation will be satisfied.
• So we can say that, $y-y_1~=~\frac{y_2-y_1}{x_2-x_1} (x-x_1)$ is the equation of the line.
   ♦ This is the equation of a line written in two-point form.
         ✰ The two points are: (x₁,y₁) and (x₂,y₂).

---

Let us see a solved example:
Solved example 10.10
Write the equations of the following lines:
(i) Line L₁, passing through (-1, -3) and (2, 4). 
(ii) Line L₂, passing through (-3, 7) and (6, 7). 
Solution:
Part (i):
• We have the two-point form: $y-y_1~=~\frac{y_2-y_1}{x_2-x_1} (x-x_1)$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{y-~-3}
&{}={}& {\frac{4-~-3}{2-~-1} (x-~-1)}
&{} \\

{\Rightarrow}&{y+3}
&{}={}& {\frac{7}{3} (x+1)}
&{} \\

{\Rightarrow}&{3y+9}
&{}={}& {7x+7}
&{} \\

{\Rightarrow}&{7x-3y-2}
&{}={}& {0}
&{} \\

\end{array}$

Part (ii):
• We have the two-point form: $y-y_1~=~\frac{y_2-y_1}{x_2-x_1} (x-x_1)$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{y-7}
&{}={}& {\frac{7-7}{6-~-3} (x-~-3)}
&{} \\

{\Rightarrow}&{y-7}
&{}={}& {\frac{0}{9} (x+3)}
&{} \\

{\Rightarrow}&{y-7}
&{}={}& {0}
&{} \\

{\Rightarrow}&{y}
&{}={}& {7}
&{} \\

\end{array}$

• The actual plots are shown in fig.10.22 below:

Fig.10.22

• Note:
In the case of L₂, we see that, it is horizontal. Indeed we obtained the slope $\frac{y_2 - y_1}{x_2 - x_1}$ = 0 for L₂

---

Slope-intercept form

• Let us first see, what intercept is. It can be written in 6 steps:
1. In fig.10.23(a) below, the line L₁ intersects the x-axis at (a,0)
• The distance of the ‘point of intersection’ from the origin O is ‘a’.
• We say that, the x-intercept of the line is +a.

Fig.10.23

2. In fig.10.23(b) above, the line L₂ intersects the x-axis at (-b,0)
• The distance of the ‘point of intersection’ from the origin O is ‘b’
• We say that, the x-intercept of the line is -b.
3. In fig.10.24(a) below, the line L₃ intersects the y-axis at (c,0)
• The distance of the ‘point of intersection’ from the origin O is ‘c’.
• We say that, the y-intercept of the line is +c.

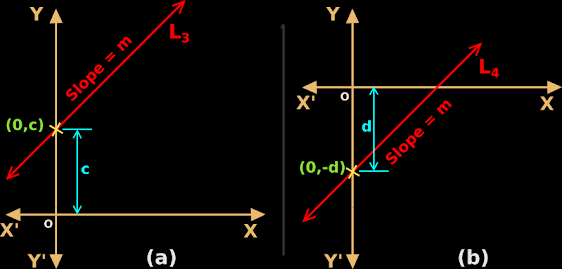Fig.10.,24

4. In fig.10.24(b) above, the line L₄ intersects the x-axis at (-d,0)
• The distance of the ‘point of intersection’ from the origin O is ‘d’
• We say that, the x-intercept of the line is -d.
5. So intercept is the distance of the point of intersection from O with the proper sign.
6. While writing intercepts, it is better to remember that:
• Any non-parallel line will intersect the x-axis.
   ♦ In some cases, the point of intersection will be on the right side of y-axis.
         ✰ Then the point of intersection will be of the type (a,0)
   ♦ In the remaining cases, the point of intersection will be on the left side of y-axis.
         ✰ Then the point of intersection will be of the type (-b,0)
• Any non-parallel line will intersect the y-axis.
   ♦ In some cases, the point of intersection will be above the x-axis.
         ✰ Then the point of intersection will be of the type (0,c)
   ♦ In the remaining cases, the point of intersection will be below the x-axis.
         ✰ Then the point of intersection will be of the type (0,-d)

---

• Suppose that, we are given the following two items:
   ♦ Slope of a line.
   ♦ x-intercept or y-intercept of the line.
• Then we can quickly write the equation of that line. Let us see how it is done.

Case I: The x-intercept is +ve.
This can be written in 4 steps:
1. Let the slope of the line be m
2. Let the x-intercept be +a
• Then we can say that, the line passes through (a,0). See fig.10.23(a) above.
3. Now we have two items:
   ♦ Slope of the line.
   ♦ A point through which the line passes.
4. So we can use the point-slope form: y-y₀ = m(x-x₀)
• Here, x₀ is 'a' and y₀ is 0
• Thus the equation becomes:
$\begin{array}{ll}
{}&{y-0}
&{}={}& {m(x-a)}
&{} \\

{\Rightarrow}&{y}
&{}={}& {m(x-a)}
&{} \\
\end{array}$

Case II: The x-intercept is -ve.
This can be written in 4 steps:
1. Let the slope of the line be m
2. Let the x-intercept be -b
• Then we can say that, the line passes through (-b,0). See fig.10.23(b) above.
3. Now we have two items:
   ♦ Slope of the line.
   ♦ A point through which the line passes.
4. So we can use the point-slope form: y-y₀ = m(x-x₀)
• Here, x₀ is '-b' and y₀ is 0
• Thus the equation becomes:
$\begin{array}{ll}
{}&{y-0}
&{}={}& {m(x- -b)}
&{} \\

{\Rightarrow}&{y}
&{}={}& {m(x+b)}
&{} \\
\end{array}$

• Based on cases I and II, we can write:
When the slope and x-intercept is given, we can use the general form: y = m(x-a)
    ♦ When the intercept is +ve, we give a +ve value for 'a'.
    ♦ When the intercept is -ve, we give a -ve value for 'a'.

Case III: The y-intercept is +ve.
This can be written in 4 steps:
1. Let the slope of the line be m
2. Let the y-intercept be +c
• Then we can say that, the line passes through (0,c). See fig.10.24(a) above.
3. Now we have two items:
   ♦ Slope of the line.
   ♦ A point through which the line passes.
4. So we can use the point-slope form: y-y₀ = m(x-x₀)
• Here, x₀ is 0 and y₀ is 'c'
• Thus the equation becomes:
$\begin{array}{ll}
{}&{y-c}
&{}={}& {m(x-0)}
&{} \\

{\Rightarrow}&{y-c}
&{}={}& {mx}
&{} \\

{\Rightarrow}&{y}
&{}={}& {mx + c}
&{} \\
\end{array}$

Case IV: The y-intercept is -ve.
This can be written in 4 steps:
1. Let the slope of the line be m
2. Let the y-intercept be -d
• Then we can say that, the line passes through (0,-d). See fig.10.24(b) above.
3. Now we have two items:
   ♦ Slope of the line.
   ♦ A point through which the line passes.
4. So we can use the point-slope form: y-y₀ = m(x-x₀)
• Here, x₀ is 0 and y₀ is '-d'
• Thus the equation becomes:
$\begin{array}{ll}
{}&{y-~-d}
&{}={}& {m(x-0)}
&{} \\

{\Rightarrow}&{y+d}
&{}={}& {mx}
&{} \\

{\Rightarrow}&{y}
&{}={}& {mx - d}
&{} \\
\end{array}$

• Based on cases III and IV, we can write:
When the slope and y-intercept is given, we can use the general form: y = mx+c
    ♦ When the intercept is +ve, we give a +ve value for 'c'.
    ♦ When the intercept is -ve, we give a -ve value for 'c'.

---

Let us see a solved example:
Solved example 10.11
Write the equations of the following lines:
(i) Line L₁ for which tan 𝜃 = 1/3 and x-intercept is 4. 
(ii) Line L₂ for which tan 𝜃 = 1/2 and y-intercept is -(11/2).
𝜃 is the inclination of the line. 
Solution:
Part (i):
• 𝜃 is the inclination of the line.  So tan 𝜃 will be the slope.
   ♦ So we can write: m = 1/3
• x-intercept is 4.
   ♦ We use the general equation: y = m(x-a)
   ♦ Here 'a' is 4.
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{y}
&{}={}& {\frac{1}{3} (x-4)}
&{} \\

{\Rightarrow}&{3y}
&{}={}& {x-4}
&{} \\

{\Rightarrow}&{x-3y-4}
&{}={}& {0}
&{} \\

\end{array}$

Part (ii):
• 𝜃 is the inclination of the line.  So tan 𝜃 will be the slope.
   ♦ So we can write: m = 1/2
• y-intercept is -(11/2).
   ♦ We use the general equation: y = mx + c
   ♦ Here 'c' is -(11/2)
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{y}
&{}={}& {\frac{1 x}{2} - \frac{11}{2}}
&{} \\

{\Rightarrow}&{2y}
&{}={}& {x-11}
&{} \\

{\Rightarrow}&{x-2y-11}
&{}={}& {0}
&{} \\

\end{array}$

• The actual plots are shown in fig.10.25 below:

Fig.10.25

• We can see that:
   ♦ L₁ intersects the x-axis at (4,0)
   ♦ L₂ intersects the x-axis at (0,-11/2)

---

In the next section, we will see intercept form and normal form.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com