In the previous section, we saw the intercept form of the equation of a line. In this section, we will see normal form.
Normal form
Let us first see what a normal is. It can be written in 3 steps:
1. 'Normal' is another word of 'perpendicular line'.
2. Suppose that, we have a line L1. We can draw another line L2 in such a way that, L2 is perpendicular to L1.
3. Then we say that, L2 is a normal to L1
• Suppose that, we are give the following two items:
♦ Length of the normal from the origin to the line
♦ Angle which the normal makes with the +ve direction of the x-axis.
• Then we can quickly write the equation of the line. Let us see how it is done.
Case I
This can be written in 5 steps:
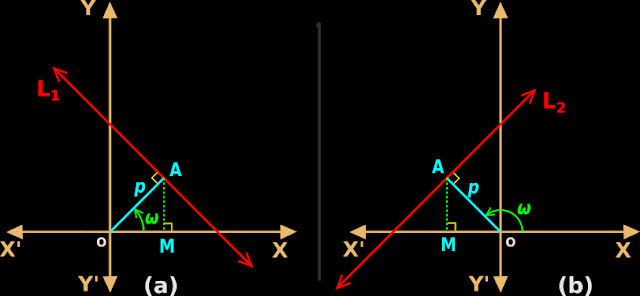
1. In fig.10.29(a) below, OA is the normal to the line L1.
• The length OA is p
• OA makes an angle of ω with the +ve direction of the x-axis.
 |
| Fig.10.29 |
2. Our first task is to find the slope of OA
• We know that, the slope of any line is the tangent of the inclination (angle with the +ve side of the x-axis).
• So the slope of OA = tan ω
3. Our next task is to find the slope of L1
• In step (2), we have calculated the slope of OA.
• OA is perpendicular to L1. So the slope of L1 will be the -ve reciprocal of the slope of OA.
• Thus we get:
Slope of L1 = $\frac{-1}{\tan \omega}$
4. Next, we want the coordinates of point A
• For that, we drop a perpendicular from A to the x-axis. M is the foot of the perpendicular.
• From the triangle OAM, we have:
♦ OM = p cos ω
♦ AM = p sin ω
• So the coordinates of A will be (p cos ω , p sin ω)
5. So now we have the slope of L1. We also have a point on L1.
• We can use the point-slope form. We get:
$\begin{array}{ll}
{}&{y-y_0}
&{}={}& {m(x-x_0)}
&{} \\
{\Rightarrow}&{y~-~p \sin \omega}
&{}={}& {\frac{-1}{\tan \omega}(x~-~p \cos \omega)}
&{} \\
{\Rightarrow}&{y~-~p \sin \omega}
&{}={}& {\frac{- \cos \omega}{\sin \omega}(x~-~p \cos \omega)}
&{} \\
{\Rightarrow}&{y \sin \omega~-~p \sin^2 \omega}
&{}={}& {-x \cos \omega~+~p \cos^2 \omega}
&{} \\
{\Rightarrow}&{x \cos \omega~+~y \sin \omega}
&{}={}& {p \sin^2 \omega~+~p \cos^2 \omega}
&{} \\
{\Rightarrow}&{x \cos \omega~+~y \sin \omega}
&{}={}& {p (\sin^2 \omega~+~ \cos^2 \omega)}
&{} \\
{\Rightarrow}&{x \cos \omega~+~y \sin \omega}
&{}={}& {p}
&{\color {green}{\text{- - - (a)}}} \\
\end{array}$
◼ Remarks:
• Line marked as (a):
sin2ω + cos2ω = 1
Case II
This can be written in 8 steps:
1. In case I, we derived an equation based on fig.10.29(a) above.
• In this fig.,
♦ the line intersects the x-axis at the +ve side.
♦ the line intersects the y-axis also at the +ve side.
2. What if
♦ the line intersect the x-axis at the -ve side.
♦ the line intersect the y-axis at the +ve side.
• Such a situation is shown in fig.10.29(b) above.
3.
But this situation should not discourage us. Because here also, we can
obtain the slope of the red line. Also we can obtain the coordinates of
A.
4. In fig.10.29(b) above, OA is the normal to the line L2.
• The length OA is p
• OA makes an angle of ω with the +ve direction of the x-axis.
5. Our first task is to find the slope of OA
• We know that, the slope of any line is the tangent of the inclination (angle with the +ve side of the x-axis).
• So the slope of OA = tan ω
•
We see that, OA is sloping downwards. That means, as we move along the
x-axis towards the +ve side, the line OA is falling. So OA must have a
-ve slope.
• Consider the angle ω in fig.10.29(b). It lies in
the second quadrant. In the second quadrant, tan is -ve. So the slope
tan ω will be -ve.
• We do not have to worry about the sign of
the slope of OA. All we need to write is that: Slope of OA is tan
ω. The ω will take care of the sign.
6. Our next task is to find the slope of L2
• In step (5), we have calculated the slope of OA.
• OA is perpendicular to L2. So the slope of L2 will be the -ve reciprocal of the slope of OA.
• Thus we get:
Slope of L2 = $\frac{-1}{\tan \omega}$
7. Next, we have to find the coordinates of point A
• For that, we drop a perpendicular from A to the x-axis. M is the foot of the perpendicular.
• From the triangle OAM, we have:
♦ OM = p cos (180 - ω) = -pcos ω
✰ See identity 9.c in the list of trigonometric identities.
♦ AM = p sin (180 - ω) = p sin ω
✰ See identity 9.d in the list of trigonometric identities.
• So the coordinates of A will be (-p cos ω , p sin ω)
•
Here also, we do not have to worry about the sign of the x-coordinate.
Since ω is in the second quadrant, cos ω will automatically
become -ve.
• We can write the coordinates of A as: (p cos ω , p sin ω)
8. So now we have the slope of L2. We also have a point on L2.
• Both are same as in case I. So we will get the same equation as in case I:
The equation of line L2 is: $x \cos \omega~+~y \sin \omega = p$
Case III
This can be written in 8 steps:
1. In case I, we derived an equation based on fig.10.29(a) above.
• In this fig.,
♦ the line intersects the x-axis at the +ve side.
♦ the line intersects the y-axis also at the +ve side.
2. What if
♦ the line intersect the x-axis at the -ve side.
♦ the line intersect the y-axis also at the -ve side.
• Such a situation is shown in fig.10.30(a) below:
 |
| Fig.10.30 |
3. But this situation should not discourage us. Because here also, we can obtain the slope of the red line. Also we can obtain the coordinates of A.
4. In fig.10.30(a) above, OA is the normal to the line L3.
• The length OA is p
• OA makes an angle of ω with the +ve direction of the x-axis.
5. Our first task is to find the slope of OA
• We know that, the slope of any line is the tangent of the inclination (angle with the +ve side of the x-axis).
• So the slope of OA = tan ω
• We see that, OA is sloping upwards. That means, as we move along the x-axis towards the +ve side, the line OA is rising. So OA must have a +ve slope.
• Consider the angle ω in fig.10.30(a). It lies in the third quadrant. In the third quadrant, tan is +ve. So the slope tan ω will be +ve.
• We do not have to worry about the sign of the slope of OA. All we need to write is that: Slope of OA is tan ω. The ω will take care of the sign.
6. Our next task is to find the slope of L3
• In step (5), we have calculated the slope of OA.
• OA is perpendicular to L3. So the slope of L3 will be the -ve reciprocal of the slope of OA.
• Thus we get:
Slope of L3 = $\frac{-1}{\tan \omega}$
7. Next, we have to find the coordinates of point A
• For that, we drop a perpendicular from A to the x-axis. M is the foot of the perpendicular.
• From the triangle OAM, we have:
♦ OM = p cos (ω - 180) = pcos [-(180 - ω)] = pcos (180 - ω) = -p cos ω
✰ See identities 2 and 9.c in the list of trigonometric identities.
♦ AM = p sin (ω - 180) = p sin [-(180 - ω)] = -p sin (180 - ω) = -p sin ω
✰ See identities 1 and 9.d in the list of trigonometric identities.
• So the coordinates of A will be (-p cos ω , -p sin ω)
• Here also, we do not have to worry about the sign of the x and y coordinates. Since ω is in the third quadrant, both sin ω and cos ω will automatically become -ve.
• We can write the coordinates of A as: (p cos ω , p sin ω)
8. So now we have the slope of L3. We also have a point on L3.
• Both are same as in case I. So we will get the same equation as in case I:
The equation of line L3 is: $x \cos \omega~+~y \sin \omega = p$
Case IV
This can be written in 8 steps:
1. In case I, we derived an equation based on fig.10.29(a) above.
• In this fig.,
♦ the line intersects the x-axis at the +ve side.
♦ the line intersects the y-axis also at the +ve side.
2. What if
♦ the line intersect the x-axis at the +ve side.
♦ the line intersect the y-axis at the -ve side.
• Such a situation is shown in fig.10.30(b) above.
3.
But this situation should not discourage us. Because here also, we can
obtain the slope of the red line. Also we can obtain the coordinates of
A.
4. In fig.10.30(b) above, OA is the normal to the line L4.
• The length OA is p
• OA makes an angle of ω with the +ve direction of the x-axis.
5. Our first task is to find the slope of OA
• We know that, the slope of any line is the tangent of the inclination (angle with the +ve side of the x-axis).
• So the slope of OA = tan ω
•
We see that, OA is sloping downwards. That means, as we move along the
x-axis towards the +ve side, the line OA is falling. So OA must have a -ve slope.
• Consider the angle ω in fig.10.30(b). It lies in
the fourth quadrant. In the fourth quadrant, tan is -ve. So the slope
tan ω will be -ve.
• We do not have to worry about the sign of
the slope of OA. All we need to write is that: Slope of OA is tan
ω. The ω will take care of the sign.
6. Our next task is to find the slope of L4
• In step (5), we have calculated the slope of OA.
• OA is perpendicular to L4. So the slope of L4 will be the -ve reciprocal of the slope of OA.
• Thus we get:
Slope of L4 = $\frac{-1}{\tan \omega}$
7. Next, we have to find the coordinates of point A
• For that, we drop a perpendicular from A to the x-axis. M is the foot of the perpendicular.
• From the triangle OAM, we have:
♦ OM = p cos (360 - ω) = pcos ω
✰ See identity 9.g in the list of trigonometric identities.
♦ AM = p sin (360 - ω) = -p sin ω
✰ See identity 9.h in the list of trigonometric identities.
• So the coordinates of A will be (p cos ω , -p sin ω)
•
Here also, we do not have to worry about the sign of the x and y coordinates.
Since ω is in the fourth quadrant, sin ω will be -ve and cos ω will be +ve.
• We can write the coordinates of A as: (p cos ω , p sin ω)
8. So now we have the slope of L4. We also have a point on L4.
• Both are same as in case I. So we will get the same equation as in case I:
The equation of line L4 is: $x \cos \omega~+~y \sin \omega = p$
• Based on the four cases, we can write:
Whatever be the orientation of the line, we can use the equation:
$x \cos \omega~+~y \sin \omega = p$
♦ The required signs will be taken care of by the angle ω.
Let us see some solved examples:
Solved example 10.12
Find
the equation of the line whose perpendicular distance from the origin
is 4 units and the angle which the normal makes with +ve direction of
x-axis is 15o
Solution:
1. Given that:
p = 4 units and ω = 15o
2. We can use the equation: $x \cos \omega~+~y \sin \omega = p$
• So we have to find cos ω and sin ω
3. We have calculated the cosine and sine of 15o in chapter 3.
♦ cos ω = cos 15 = $\frac{\sqrt{3} + 1}{2 \sqrt{2}}$
♦ sin ω = sin 15 = $\frac{\sqrt{3} - 1}{2 \sqrt{2}}$
4. Substituting the known values in the equation in (2), we get:
$\begin{array}{ll}
{}&{x \cos \omega~+~y \sin \omega}
&{}={}& {p}
&{} \\
{\Rightarrow}&{\frac{(\sqrt{3} + 1)x}{2 \sqrt{2}}~+~\frac{(\sqrt{3} - 1)y}{2 \sqrt{2}}}
&{}={}& {4}
&{} \\
{\Rightarrow}&{(\sqrt{3} + 1)x~+~(\sqrt{3} - 1)y}
&{}={}& {8\sqrt{2}}
&{} \\
\end{array}$
5. The actual plot is shown in fig.10.31 below:
 |
| Fig.10.31 |
(i) The red line is the line for which we determined the equation.
(ii) Note the magenta dashed arc. It is drawn with center as O.
• This arc passes through:
♦ The point of intersection of the cyan and red lines.
♦ The point (0,4)
• So it is clear that, the length of the cyan line is four units.
Solved example 10.13
The Fahrenheit temperature F and
absolute temperature K satisfy a linear relation. Given that K = 273
when F = 32 and that K = 373 when F = 212. Express K in terms of F and
find the value of F, when K = 0
Solution:
1. Given that: Fahrenheit temperature F and absolute temperature K satisfy a linear relation.
That means, if we plot the relation between F and K on a graph paper, the plot will be a straight line.
2. Also given that:
♦ K = 273 when F = 32
✰ This is just like: when x = 32, y is 273
♦ K = 373 when F = 212.
✰ This is just like: when x = 212, y is 373
• So we have two points on the straight line: (32, 273) and (212, 373).
3. It is important to keep in mind that, the points are in the form (F, K).
• That means,
♦ F is plotted along the x-axis.
♦ K is plotted along the y-axis.
4. We have two points on the line. So we can use the two point form:
$y-y_1~=~\frac{y_2 - y_1}{x_2 - x_1}(x-x_1)$
• For our present problem, we can modify this as:
$K-K_1~=~\frac{K_2 - K_1}{F_2 - F_1}(F-F_1)$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{K-K_1}
&{}={}& {\frac{K_2 - K_1}{F_2 - F_1}(F-F_1)}
&{} \\
{\Rightarrow}&{K-273}
&{}={}& {\frac{373 - 273}{212 - 32}(F-32)}
&{} \\
{\Rightarrow}&{K-273}
&{}={}& {\frac{100}{180}(F-32)}
&{} \\
{\Rightarrow}&{K-273}
&{}={}& {\frac{5}{9}(F-32)}
&{} \\
{\Rightarrow}&{9K-2457}
&{}={}& {5F-160}
&{} \\
{\Rightarrow}&{9K}
&{}={}& {5F+2297}
&{} \\
{\Rightarrow}&{K}
&{}={}& {\frac{5F}{9}+\frac{2297}{9}}
&{} \\
\end{array}$
• Thus we get a relation between K and F.
5. We want the value of F when K = 0
For that, we put K = 0 in the above relation. We get:
$\begin{array}{ll}
{}&{K}
&{}={}& {\frac{5F}{9}+\frac{2297}{9}}
&{} \\
{\Rightarrow}&{0}
&{}={}& {\frac{5F}{9}+\frac{2297}{9}}
&{} \\
{\Rightarrow}&{\frac{5F}{9}}
&{}={}& {-\frac{2297}{9}}
&{} \\
{\Rightarrow}&{5F}
&{}={}& {-2297}
&{} \\
{\Rightarrow}&{F}
&{}={}& {-459.4}
&{} \\
\end{array}$
6. The actual plot is shown in fig.10.32 below:
 |
| Fig.10.32 |
• Points A and B represent the given data.
• Point C represent the value of F when K is zero.
The link to a few more solved examples is given below:
In the next section, we will see General equation of a line.
No comments:
Post a Comment