Chapter 3.10 - Domain and Range of Tangent and Cotangent Functions

In the previous section, we saw the domain and range of cosine and secant functions. In this section, we will see the domain and range of tangent and cotangent functions.

Let us find the domain and range of f(x) = tan x. It can be written in 2 steps:
1. First we will find the domain:
• We have seen that:
    ♦ In the case of f(x) = tan x,
    ♦ $\frac{(2n+1)\pi}{2}$ where n is any integer, should not be used as input x
• So we can write:
Domain of f(x) = csc x is $R-\{x:x=\frac{(2n+1)\pi}{2},\; n\, \in \,Z\}$
• That means, we must subtract the set $\{x:x=\frac{(2n+1)\pi}{2},\; n\, \in \,Z\}$ from R. The resulting set after subtraction, is the domain of f(x) = tan x
• $\{x:x=\frac{(2n+1)\pi}{2},\; n\, \in \,Z\}$ is the set containing all $\frac{(2n+1)\pi}{2}$, where n is any integer.
2. Let us find the range of f(x) = tan x
• The range in this case can be better understood if we analyze the graph of f(x) = cos x and f(x) = sec x and f(x) = tan x together. It is shown in fig.3.32 below:

Fig.3.32

A basic analysis of this graph is given below:
(i) Consider the segment from 0 to $\frac{\pi}{2}$ on the x axis.
• In this segment,
   ♦ the sine curve rises
   ♦ the cosine curve falls
   ♦ the tangent curve rises
• Let us see the reason for the rise in tangent curve:
   ♦ We have: $\tan x= \frac{\sin x}{\cos x}$
   ♦ The rise in sine curve indicates increase in numerator.
   ♦ The fall in cosine curve indicates decrease in denominator.
   ♦ So the fraction $\frac{\sin x}{\cos x}$ will obviously increase.
• At zero angle, sine is 0 and cosine is 1
   ♦ So tangent will be zero. This is clearly visible in the graph
• At $\frac{\pi}{2}$ angle, sine is 1 and cosine is 0
   ♦ So tangent can not be defined.
   ♦ Indeed we see that, the tangent curve do not touch the vertical line through $\frac{\pi}{2}$
• As the angle approaches $\frac{\pi}{2}$, the cosine value becomes very small and consequently the tangent becomes very large.

◼ As seen before, we cannot put x = $\frac{\pi}{2}$ in $f(x) = \tan x = \frac{\sin x}{\cos x}$. We can write: • As x approaches $\frac{\pi}{2}$, cos x becomes smaller and smaller, getting closer and closer to zero. (For example, values like 0.00001, 0.000001 are very close to zero) • As cos x becomes smaller and smaller, tan x becomes larger and larger. • This is indicated by the rising portion of the tangent curve between 0 and $\frac{\pi}{2}$. • As angle becomes closer and closer to $\frac{\pi}{2}$, this rising portion gets closer and closer to the vertical line through $\frac{\pi}{2}$. (why does this happen? The reader may write the answer in his/her own notebooks) • But it never touches that vertical line. • If it touch, it would mean that, x = $\frac{\pi}{2}$ is a point in the tangent curve. We know that, it cannot happen.

(ii) In a similar way, the reader must be able to analyze the remaining segments:
   ♦ $\frac{\pi}{2}$ to π
   ♦ π to $\frac{3\pi}{2}$
   ♦ $\frac{3\pi}{2}$ to 2π
(iii) When all the segments are analyzed, we get a good understanding about the pattern.
3. We see that the tangent curves extend from very high up to very low bottom in the graph. There is no break. That means, all values in the y axis are present in the curves.
• We can write: Range of f(x) = tan x is R

---

Let us find the domain and range of f(x) = cot x. It can be written in 2 steps:
1. First we will find the domain:
• We have seen that:
    ♦ In the case of f(x) = cot x,
    ♦ nπ, where n is any integer, should not be used as input x
• So we can write:
Domain of f(x) = cot x is $R-\{x:x=n \pi,\; n\, \in \,Z\}$
• That means, we must subtract the set $\{x:x=n \pi,\; n\, \in \,Z\}$ from R. The resulting set after subtraction, is the domain of f(x) = cot x
• $\{x:x=n \pi,\; n\, \in \,Z\}$ is the set containing all nπ, where n is any integer.
2. Let us find the range of f(x) = cot x
• The range in this case can be better understood if we analyze the graph of f(x) = tan x and f(x) = cot x together. It is shown in fig.3.33 below:

Fig.3.33

A basic analysis of this graph is given below:
(i) Consider the segment from 0 to $\frac{\pi}{2}$ on the x axis.
• In this segment,
   ♦ the tangent curve rises
   ♦ the cotangent curve falls
   ♦ this is obvious because, cot is the reciprocal of tan
• At zero angle, tan is zero
   ♦ The reciprocal of zero does not exist.
   ♦ So at zero angle, the reciprocal of tan is not defined.
   ♦ Indeed we see that, the cot curve do not touch the vertical line through 0
(ii) The reader must be able to explain the whole pattern of cot in this way.
(iii) Note that, the sign does not change in the reciprocal
   ♦ If tan is +ve in a segment, cot will also be +ve in that segment.
   ♦ If tan is -ve in a segment, cot will also be -ve in that segment.
3. We see that the cotangent curves extend from very high up to very low bottom in the graph. There is no break. That means, all values in the y axis are present in the curves.
• We can write: Range of f(x) = cot x is R.

---

In the next section, we will see trigonometric identities.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 3.9 - Domain and Range of Cosine and Secant Functions

In the previous section, we saw the domain and range of sine and cosecant functions. In this section, we will see the domain and range of cosine and secant functions.

Let us find the domain and range of f(x) = cos x. It can be written in 2 steps:
1. First we will find the domain:
• We have seen that:
In the case of f(x) = cos x, any real number can be used as input x.
• So we can write: Domain of f(x) = cos x, is the set R.
(Recall that, R is the set of real numbers)
2. Let us find the range of f(x) = cos x
• The range in this case can be better understood if we analyze the graph of f(x) = cos x. It is shown in fig.3.29 below:

Fig.3.29

• The graph of f(x) = sin x, which we saw in the previous section, is given again below. This is for a comparison.

Fig.3.26

• An analysis of the cosine graph can be written in 3 steps:
(i) We already know the reason for the markings $\frac{\pi}{2},\; \pi,\; \frac{3\pi}{2},\; 2\pi,\; \frac{5\pi}{2}$ so on . . . on the x axis.
(ii) Now let us consider the output y values.
• We see that, whatever be the value of input x,
   ♦ Output y value (that is., cosine of x) never becomes greater than 1
   ♦ Output y value never becomes lesser than -1
(iii) We can mark any point on the red curve in the graph. The y coordinate of that point will be either 1 or -1 or a value between 1 and -1.
◼ So the range can be written as [-1, 1]
• That means:
   ♦ All real values between -1 and 1 are included in the range.
   ♦ Left side '[' indicates that -1 is also included in the range.
   ♦ Right side ']' indicates that +1 is also included in the range.

---

• We just saw that, cosine value can never rise above -1. Neither can it fall below -1.
• The reason can be written in 8 steps:
1. In the animation in fig.3.30 below, the thick white horizontal line is the base of the triangle in our familiar unit circle.

Fig.3.30

• We know that, this base is related to the cosine value of the angle.
2. The red ray starts to rotate from the +ve side of the x axis.
• Since the green circle is a unit circle, the length of the horizontal white line at this initial point will be 1
• As the rotation proceeds, the length of the horizontal line gradually decreases.
• It becomes zero when the ray completes a rotation of ${\frac{\pi}{2}}^c$. That is, when the ray coincides with the y axis.
• So we can write:
(i) The cosine value start to decrease from 1 (when the ray coincides with the +ve side of x axis)
(ii) The cosine value attains a value of 0 (when the ray coincides with the +ve side of y axis)
(iii) This decrease of cosine value, from 1 to zero, is indicated by the falling portion between x = 0 and x = $\frac{\pi}{2}$ in the graph in fig.3.29 above.
3. Next, the red ray proceeds to rotate from x = $\frac{\pi}{2}$ to x = π.
• We see that, the length of the horizontal white line increases from zero to 1.
• Though it is an 'increase in length', it happens on the negative side of the x axis. On this negative side, every x coordinate is negative, That means, on the negative side of the x axis, every cosine value is negative.
• As the length increases, the negative value increases. So in effect, it is a decrease.
• This decrease is indicated by the falling portion between x = $\frac{\pi}{2}$ and x = π in the graph in fig.3.29 above.
4. Next, the red ray proceeds to rotate from x = π to x = $\frac{3\pi}{2}$.
• We see that, the length of the horizontal white line decreases from 1 to zero.
• Though it is a 'decrease in length', it happens on the negative side of the x axis. On this negative side, every x values is negative, That means, on the negative side of the x axis, every cosine value is negative.
• As the length decreases, the negative value decreases. So in effect, it is an increase.
• This increase is indicated by the rising portion between x = π and x = $\frac{3\pi}{2}$ in the graph in fig.3.29 above.
5. Next, the red ray proceeds to rotate from x = $\frac{3\pi}{2}$ to x = 2π.
• We see that, the length of the horizontal white line increases from zero to 1.
• This increase is indicated by the rising portion between x = $\frac{3\pi}{2}$ and x = 2π in the graph in fig.3.29 above.
6. As the ray continues to rotate, this pattern repeats again and again. Thus we get the wave form on the positive side of the x axis in the graph.
7. Similar steps can be written for rotation in the anticlockwise direction also. Based on those steps, we will be able to explain the wave form on the negative side of the x axis in the graph.
8. Note that:
• In the first ${\frac{\pi}{2}}^c$ rotation in the anticlockwise direction, there is a fall in cosine value.
• In the first ${\frac{\pi}{2}}^c$ rotation in the clockwise direction also, there is a fall in cosine value.
• So there is a smooth transition between the two waves on either sides of the x axis.

---

Let us find the domain and range of f(x) = sec x. It can be written in 4 steps:
1. First we will find the domain:
• We have seen that:
    ♦ In the case of f(x) = sec x,
    ♦ $\frac{(2n+1)\pi}{2}$ where n is any integer, should not be used as input x
• So we can write:
Domain of f(x) = sec x is $R-\{x:x=\frac{(2n+1)\pi}{2},\; n\, \in \,Z\}$
• That means, we must subtract the set $\{x:x=\frac{(2n+1)\pi}{2},\; n\, \in \,Z\}$ from R. The resulting set after subtraction, is the domain of f(x) = sec x
• $\{x:x=\frac{(2n+1)\pi}{2},\; n\, \in \,Z\}$ is the set containing all $\frac{(2n+1)\pi}{2}$, where n is any integer.
2. Let us find the range of f(x) = sec x
• The range in this case can be better understood if we analyze the graph of f(x) = cos x and f(x) = sec x together. It is shown in fig.3.31 below:

Fig.3.31

An analysis of this graph can be written in 6 steps:
(i) Consider the segment from 0 to $\frac{\pi}{2}$ on the x axis.
• In this segment,
   ♦ the cosine curve falls
   ♦ but the secant curve rises.
• That means, when the angle increases from 0 to $\frac{\pi}{2}$,
   ♦ the cosine value decreases
   ♦ but the secant value increases.
• This is obvious because, secant is the reciprocal of cosine.
• In the segment from 0 to $\frac{\pi}{2}$, the maximum value of cosine occurs at zero
   ♦ So the minimum value of secant should also be at zero. 
   ♦ Indeed we see that, the rise of the secant curve occurs after zero.
• The value of cosine at zero is 1
   ♦ The value of secant at zero should be the reciprocal of 1, which is 1.
   ♦ Indeed we see that, the value of secant at zero is 1.
• The value of cosine at $\frac{\pi}{2}$ is 0
   ♦ The value of secant at $\frac{\pi}{2}$ should be the reciprocal of 0, which is not defined
   ♦ Indeed we see that, the value of secant curve never touches the vertical line through $\frac{\pi}{2}$
• As the angle approaches $\frac{\pi}{2}$, the cosine value becomes very small and consequently the secant which is the reciprocal, becomes very large.

◼ As seen before, we cannot put x = $\frac{\pi}{2}$ in $f(x) = \sec x = \frac{1}{\cos x}$. We can write: • As x approaches $\frac{\pi}{2}$, cos x becomes smaller and smaller, getting closer and closer to zero. (For example, values like 0.00001, 0.000001 are very close to zero) • As cos x becomes smaller and smaller, the reciprocal sec x becomes larger and larger. • This is indicated by the rising portion of the secant curve between 0 and $\frac{\pi}{2}$. • As angle becomes closer and closer to $\frac{\pi}{2}$, this rising portion gets closer and closer to the vertical line through $\frac{\pi}{2}$. (why does this happen? The reader may write the answer in his/her own notebooks) • But it never touches that vertical line. • If it touch, it would mean that, x = $\frac{\pi}{2}$ is a point in the secant curve. We know that, it cannot happen.

(ii) Consider the segment from $\frac{\pi}{2}$ to π on the x axis.
• In this segment,
   ♦ the cosine curve falls
   ♦ but the secant curve rises.
• That means, when the angle increases from $\frac{\pi}{2}$ to π,
   ♦ the cosine value decreases (increases negatively)
   ♦ but the secant value increases (decreases negatively).
• This is obvious because, secant is the reciprocal of cosine
Note that here, all the cosine values are -ve. Consequently, all the secant values will also be -ve.
• In the segment from $\frac{\pi}{2}$ to π, the minimum value of cosine occurs at π.
  ♦ So the maximum value of secant should also be at π.
  ♦ Indeed we see that, at π, the secant is at it's peak point in this segment.
  ♦ The value is reciprocal of -1, which is -1
(iii) Consider the segment from π to $\frac{3\pi}{2}$ on the x axis.
• In this segment,
   ♦ the cosine curve rises
   ♦ but the secant curve falls.
• That means, when the angle increases from π to $\frac{3\pi}{2}$,
   ♦ the cosine value increases
   ♦ but the secant value decreases.
• This is obvious because, secant is the reciprocal of cosine.
Note that here, all the cosine values are -ve. Consequently, all the secant values will also be -ve.
• In the segment from π to $\frac{3\pi}{2}$, the maximum value of cosine occurs at $\frac{3\pi}{2}$.
  ♦ So the minimum value of secant should also be at $\frac{3\pi}{2}$.
  ♦ Indeed we see that, as the angle approaches $\frac{3\pi}{2}$, the secant curve goes further and further down.

◼ As seen before, we cannot put x = $\frac{3\pi}{2}$ in $f(x) = \sec x = \frac{1}{\cos x}$. We can write: • As x approaches $\frac{3\pi}{2}$, cos x becomes smaller and smaller (negatively), getting closer and closer to zero. (For example, values like -0.00001, -0.000001 are very close to zero) • As cos x becomes smaller and smaller, the reciprocal sec x becomes larger and larger (negatively). • This is indicated by the falling portion of the secant curve between π and $\frac{3\pi}{2}$. • As angle becomes closer and closer to $\frac{3\pi}{2}$, this falling portion gets closer and closer to the vertical line through $\frac{3\pi}{2}$. (why does this happen? The reader may write the answer in his/her own notebooks) • But it never touches that vertical line. • If it touch, it would mean that, x = $\frac{3\pi}{2}$ is a point in the secant curve. We know that, it cannot happen.

(iv) Consider the segment from $\frac{3\pi}{2}$ to 2π on the x axis.
• In this segment,
   ♦ the cosine curve rises
   ♦ but the secant curve falls.
• That means, when the angle increases from $\frac{3\pi}{2}$ to 2π,
   ♦ the cosine value increases
   ♦ but the secant value decreases.
• This is obvious because, secant is the reciprocal of cosine.
Note that here, all the cosine values are +ve. Consequently, all the secant values will also be +ve.

(v) Now we have a basic idea about how the 'U' shapes and 'inverted U' shapes are formed in positive side of the x axis.
As the angle increases beyond 2π, this pattern repeats again and again.
(vi) Similar steps can be written for negative angles also. Those steps will explain the 'U' shapes and 'inverted U' shapes in the negative side of the x axis.
3. Based on the analysis of the graph, we can write:
• The output of f(x) = sec x can be any +ve real number starting from +1 and higher.
• The output of f(x) = sec x can be any -ve real number starting from -1 and lower.
• The values lying between -1 and +1 cannot be output values.
4. So the range of f(x) = sec is R - (-1, +1)
• That means, we have to subtract the set (-1, +1) from the the set of real numbers R
• The resulting set after subtraction is the range of f(x) = sec x
• (-1, +1) indicates that:
   ♦ all values between -1 and +1 are included in the set.
   ♦ '(' on the left side indicates that -1 is not included in the set.
   ♦ ')' on the right side indicates that +1 is not included in the set.
• So it is clear that, the two values -1 and +1 should not be subtracted from R.

---

In the next section, we will see domain and range of tangent and cotangent functions.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 3.8 - Domain and Range of Sine and Cosecant Functions

In the previous section, we saw that any real number can be used as input x for f(x) = sin x and f(x) = cos x. So we get the feeling that, any real number can be used as input x for tan x, sec x etc., also. But it is not true. There are some exceptions. It can be written in 4 steps:

1. Consider f(x) = tan x.
• This can be written as $f(x)=\frac{\sin x}{\cos x}$
    ♦ So it is obvious that, cos x should not become zero.
• If we use an input x which makes cos x equal to zero, we will not get an output for the function f(x) = tan x.
• We know the exact x values for which cos x becomes zero. They are: $(2n+1)\frac{\pi}{2}$, where n is any integer.
◼ So we can write:
f(x) = tan x = $\frac{\sin x}{\cos x},\;x \neq (2n+1)\frac{\pi}{2}$ where n is any integer.
2. Consider f(x) = csc x.
• This can be written as $f(x)=\frac{1}{\sin x}$
    ♦ So it is obvious that, sin x should not become zero.
• If we use an input x which makes sin x equal to zero, we will not get an output for the function f(x) = csc x.
• We know the exact x values for which sin x becomes zero. They are: nπ, where n is any integer.
◼ So we can write:
f(x) = csc x = $\frac{1}{\sin x},\;x \neq n \pi$ where n is any integer.
3. Consider f(x) = sec x.
• This can be written as $f(x)=\frac{1}{\cos x}$
    ♦ So it is obvious that, cos x should not become zero.
• If we use an input x which makes cos x equal to zero, we will not get an output for the function f(x) = sec x.
• We know the exact x values for which cos x becomes zero. They are: $(2n+1)\frac{\pi}{2}$, where n is any integer.
◼ So we can write:
f(x) = sec x = $\frac{1}{\cos x},\;x \neq (2n+1)\frac{\pi}{2}$ where n is any integer.
4. Consider f(x) = cot x.
• This can be written as $f(x)=\frac{\cos x}{\sin x}$
    ♦ So it is obvious that, sin x should not become zero.
• If we use an input x which makes sin x equal to zero, we will not get an output for the function f(x) = cot x.
• We know the exact x values for which sin x becomes zero. They are: nπ, where n is any integer.
◼ So we can write:
f(x) = cot x = $\frac{\cos x}{\sin x},\;x \neq n \pi$ where n is any integer.

---

Sign of trigonometric functions

This can be written in 4 steps:
1. Consider the unit circle that we saw in the previous sections. In that circle, we have three important items:
(i) The tip of the ray.
   ♦ We denoted it as P.
(ii) Base of the triangle OMP.
   ♦ We denoted it as a
(iii) Altitude of the triangle OMP.
   ♦ We denoted it as b
2. We know that:
Coordinates of P are written using a and b.
3. We also know that:
  ♦ a is related to cosine
  ♦ b is related to sine
4. Based on steps (1), (2) and (3), we can write about the four quadrants:
First quadrant
(i) If P is in the I quadrant, the coordinates of P will be (a, b)
(ii) We know that:
   ♦ x coordinate is the cosine.
   ♦ y coordinate is the sine.
(iii) So in the I quadrant, cosine will be +ve, sine will be +ve.
• Consequently,
sec will be +ve, csc will be +ve.
• Also,
tan will be +ve, cot will be +ve
(iv) Thus we get the column named I in the table 3.1 below:

Table 3.1

• Note that, the ray can rotate in the anticlockwise direction (to give a positive angle) and reach the I quadrant.
• The ray can also rotate in the clockwise direction (to give a negative angle) and reach the I quadrant.
• What ever be the direction of rotation, the coordinates of P will not change. So the signs written in the column named I of table 3.1 is valid for both +ve and -ve angles.

Second quadrant
(i) If P is in the II quadrant, the coordinates of P will be (-a, b)
(ii) We know that:
   ♦ x coordinate is the cosine.
   ♦ y coordinate is the sine.
(iii) So in the II quadrant, cosine will be -ve, sine will be +ve.
• Consequently,
sec will be -ve, csc will be +ve.
• Also,
tan will be -ve, cot will be -ve
(iv) Thus we get the column named II in the table 3.1 above.
• Note that, the ray can rotate in the anticlockwise direction (to give a positive angle) and reach the II quadrant.
• The ray can also rotate in the clockwise direction (to give a negative angle) and reach the II quadrant.
• What ever be the direction of rotation, the coordinates of P will not change. So the signs written in the column named II of table 3.1 is valid for both +ve and -ve angles. 

Third quadrant
(i) If P is in the III quadrant, the coordinates of P will be (-a, -b)
(ii) We know that:
   ♦ x coordinate is the cosine.
   ♦ y coordinate is the sine.
(iii) So in the III quadrant, cosine will be -ve, sine will be -ve.
• Consequently,
sec will be -ve, csc will be -ve.
• Also,
tan will be +ve, cot will be +ve
(iv) Thus we get the column named III in the table 3.1 above.
• Note that, the ray can rotate in the anticlockwise direction (to give a positive angle) and reach the III quadrant.
• The ray can also rotate in the clockwise direction (to give a negative angle) and reach the III quadrant.
• What ever be the direction of rotation, the coordinates of P will not change. So the signs written in the column named III of table 3.1 are valid for both +ve and -ve angles. 

Fourth quadrant
(i) If P is in the IV quadrant, the coordinates of P will be (a, -b)
(ii) We know that:
   ♦ x coordinate is the cosine.
   ♦ y coordinate is the sine.
(iii) So in the IV quadrant, cosine will be +ve, sine will be -ve.
• Consequently,
sec will be +ve, csc will be -ve.
• Also,
tan will be -ve, cot will be -ve
(iv) Thus we get the column named IV in the table 3.1 above.
• Note that, the ray can rotate in the anticlockwise direction (to give a positive angle) and reach the IV quadrant.
• The ray can also rotate in the clockwise direction (to give a negative angle) and reach the IV quadrant.
• What ever be the direction of rotation, the coordinates of P will not change. So the signs written in the column named IV of table 3.1 are valid for both +ve and -ve angles.

---

Domain and range of trigonometric functions

This can be explained in 2 steps:
1. We know that:
• Domain of a function is the set containing all the input x values.
• Range of a function is the set containing all the output y [y is same as f(x)] values.
2. We need to have a basic idea about the domain and range of the various trigonometric functions like f(x) = sin x, f(x) = cos x, f(x) = sec x etc.,

---

Let us find the domain and range of f(x) = sin x. It can be written in 2 steps:
1. First we will find the domain:
• We have seen that:
In the case of f(x) =sin x, any real number can be used as input x.
• So we can write: Domain of f(x) = sin x, is the set R.
(Recall that, R is the set of real numbers)
2. Let us find the range of f(x) = sin x
The range in this case can be better understood if we analyze the graph of f(x) = sin x. It is shown in fig.3.26 below:

Fig.3.26

• An analysis of this graph can be written in 4 steps:
(i) We see that, on the x axis, the markings are: $\frac{\pi}{2},\; \pi,\; \frac{3\pi}{2},\; 2\pi,\; \frac{5\pi}{2}$ so on . . .
• Normally, we expect markings as: 1, 2, 3, . . . OR  5, 10, 15, . . .
• The markings in the above graph are no different from 1, 2, 3, . . . OR  5, 10, 15, .
• If we use the real number line as the x axis, this type of marking can be achieved by putting marks at $\frac{3.14}{2},\; 3.14,\; \frac{3\times 3.14}{2},\; 2\times 3.14,\; \frac{5\times 3.14}{2}$ so on . . .
• Here each unit on the x axis is ${\frac{\pi}{2}}^c$
• These markings can go up to +∞. That means, all positive real numbers can be used as input x.
• They are positive angles obtained when the ray rotates in the anticlockwise direction.
(ii) Similar is the case with markings on the negative side of the x axis.
• They are negative angles, which are obtained when the ray rotates in the clockwise direction.
• The -ve markings can go up to -∞. That means, all negative real numbers can be used as input x.
(iii) Now let us consider the output y values.
• We see that, whatever be the value of input x,
   ♦ Output y value (that is., sine of x) never becomes greater than 1
   ♦ Output y value never becomes lesser than -1
(iv) We can mark any point on the red curve in the graph. The y coordinate of that point will be either 1 or -1 or a value between 1 and -1.
◼ So the range can be written as [-1, 1]
• That means:
   ♦ All real values between -1 and 1 are included in the range.
   ♦ Left side '[' indicates that -1 is also included in the range.
   ♦ Right side ']' indicates that +1 is also included in the range.

---

• We just saw that sine value can never rise above +1. Neither can it fall below -1.
• The reason can be written in 8 steps:
1. In the animation in fig.3.27 below, the thick white vertical line is the altitude of the triangle in our familiar unit circle.

Fig.3.27

• We know that, this altitude is related to the sine value of the angle.
2. The red ray starts to rotate from the +ve side of the x axis.
• As the rotation proceeds, the length of the white vertical line gradually increases.
• It becomes maximum when the ray completes a rotation of ${\frac{\pi}{2}}^c$. That is, when the ray coincides with the y axis.
• Since the green circle is a unit circle, the length of the vertical white line at this point will be 1
• So we can write:
(i) The sine value start to increase from zero (when the ray coincides with the +ve side of x axis)
(ii) The sine value attains a maximum value of 1 (when the ray coincides with the +ve side of y axis)
(iii) This increase of sine value, from zero to 1, is indicated by the rising portion between x = 0 and x = $\frac{\pi}{2}$ in the graph in fig.3.26 above.
3. Next, the red ray proceeds to rotate from x = $\frac{\pi}{2}$ to x = π.
• We see that, the length of the vertical white line decreases from 1 to zero.
• This decrease is indicated by the falling portion between x = $\frac{\pi}{2}$ and x = π in the graph in fig.3.26 above.
4. Next, the red ray proceeds to rotate from x = π to x = $\frac{3\pi}{2}$.
• We see that, the length of the vertical white line increases from zero to 1.
• Though it is an 'increase in length', it happens below the x axis. Below the x axis, every y coordinate is negative. That means, below the y axis, every sine value is negative.
• As the length increases, the negative value increases. So in effect, it is a decrease.
• This decrease is indicated by the falling portion between x = π and x = $\frac{3\pi}{2}$ in the graph in fig.3.26 above.
5. Next, the red ray proceeds to rotate from x = $\frac{3\pi}{2}$ to x = 2π.
• We see that, the length of the vertical white line decreases from 1 to zero.
• Though it is a 'decrease in length', it happens below the x axis. Below the x axis, every y coordinate is negative, That means, below the y axis, every sine value is negative.
• As the length decreases, the negative value decreases. So in effect, it is an increase.
• This increase is indicated by the rising portion between x = $\frac{3\pi}{2}$ and x = 2π in the graph in fig.3.26 above.
6. As the ray continues to rotate, this pattern repeats again and again. Thus we get the wave form on the positive side of the x axis in the graph.
7. Similar steps can be written for rotation in the anticlockwise direction also. Based on those steps, we will be able to explain the wave form on the negative side of the x axis in the graph.
8. Note that:
• In the first ${\frac{\pi}{2}}^c$ rotation in the anticlockwise direction, there is a rise in sine value.
• In the first ${\frac{\pi}{2}}^c$ rotation in the clockwise direction, there is a fall in sine value.
• So there is a smooth transition between the two waves on either sides of the x axis.

---

Let us find the domain and range of f(x) = csc x. It can be written in 4 steps:
1. First we will find the domain:
• We have seen that:
    ♦ In the case of f(x) = csc x,
    ♦ nπ where n is any integer, should not be used as input x
• So we can write:
Domain of f(x) = csc x is R -{x : x = nπ, n ∈ Z}
• That means, we must subtract {x : x = nπ, n ∈ Z} from R. The resulting set after subtraction, is the domain of f(x) = csc x
• {x : x = nπ, n ∈ Z} is the set containing all nπ, where n is any integer.
2. Let us find the range of f(x) = csc x
We know that, csc is the reciprocal of sine. So the range of f(x) = csc x can be better understood if we analyze the graph of f(x) = sin x and f(x) = csc x together. It is shown in fig.3.28 below:

Fig.3.28

An analysis of this graph can be written in 6 steps:
(i) Consider the segment from 0 to $\frac{\pi}{2}$ on the x axis.
• In this segment,
   ♦ the sine curve rises
   ♦ but the csc curve falls.
• That means, when the angle increases from 0 to $\frac{\pi}{2}$,
   ♦ the sine value increases
   ♦ but the csc value decreases.
• This is obvious because, csc is the reciprocal of sine
• In the segment from 0 to $\frac{\pi}{2}$, the maximum value of sine occurs at $\frac{\pi}{2}$
   ♦ So the minimum value of csc should also be at $\frac{\pi}{2}$   
   ♦ Indeed we see that, the fall of the csc curve occurs upto $\frac{\pi}{2}$.
   ♦ Thereafter, it rises.
• The value of sine at $\frac{\pi}{2}$ is 1
   ♦ The value of csc at $\frac{\pi}{2}$ should be the reciprocal of 1, which is 1
   ♦ Indeed we see that, the value of csc at $\frac{\pi}{2}$ is 1
(ii) Consider the segment from $\frac{\pi}{2}$ to π on the x axis.
• In this segment,
   ♦ the sine curve falls
   ♦ but the csc curve rises.
• That means, when the angle increases from $\frac{\pi}{2}$ to π,
   ♦ the sine value decreases
   ♦ but the csc value increases.
• This is obvious because, csc is the reciprocal of sine
• In the segment from $\frac{\pi}{2}$ to π, the minimum value of sine occurs at π.
  ♦ So the maximum value of csc should also be at π.
  ♦ Indeed we see that, as π approaches, the csc curve rises further and further up.

◼ As seen before, we cannot put x = π in $f(x) = \csc x = \frac{1}{\sin x}$. We can write: • As x approaches π, sin x becomes smaller and smaller, getting closer and closer to zero. (For example, values like 0.00001, 0.000001 are very close to zero) • As sin x becomes smaller and smaller, the reciprocal csc x becomes larger and larger. • This is indicated by the rising portion of the csc curve between $\frac{\pi}{2}$ and π. • As angle becomes closer and closer to π, this rising portion gets closer and closer to the vertical line through π. (why does this happen? The reader may write the answer in his/her own notebooks) • But it never touches that vertical line. • If it touch, it would mean that, x = π is a point in the csc curve. We know that, it cannot happen.

(iii) Consider the segment from π to $\frac{3\pi}{2}$ on the x axis.
• In this segment,
   ♦ the sine curve falls
   ♦ but the csc curve rises.
• That means, when the angle increases from π to $\frac{3\pi}{2}$,
   ♦ the sine value decreases
   ♦ but the csc value increases.
• This is obvious because, csc is the reciprocal of sine.
Note that here, all the sine values are -ve. Consequently, all the csc values will also be -ve.
• In the segment from π to $\frac{3\pi}{2}$, the minimum value of sine occurs at $\frac{3\pi}{2}$.
  ♦ So the maximum value of csc should also be at $\frac{3\pi}{2}$.
   ♦ Indeed we see that, the rise of the csc curve occurs upto $\frac{3\pi}{2}$.
   ♦ Thereafter, it falls.
• The value of sine at $\frac{3\pi}{2}$ is -1
   ♦ The value of csc at $\frac{3\pi}{2}$ should be the reciprocal of -1, which is -1.
   ♦ Indeed we see that, the value of csc at $\frac{3\pi}{2}$ is -1.
• Consider the portion just after π. The sine values here will be very small negative values. Consequently, the csc values here will be very large negative values. This fact can be clearly seen in the graphs.
(iv) Consider the segment from $\frac{3\pi}{2}$ to 2π on the x axis.
• In this segment,
   ♦ the sine curve rises
   ♦ but the csc curve falls.
• That means, when the angle increases from $\frac{3\pi}{2}$ to 2π,
   ♦ the sine value increases
   ♦ but the csc value decreases.
• This is obvious because, csc is the reciprocal of sine.
Note that here, all the sine values are -ve. Consequently, all the csc values will also be -ve.

◼ As seen before, we cannot put x = 2π in $f(x) = \csc x = \frac{1}{\sin x}$. We can write: • As x approaches 2π, sin x becomes smaller and smaller (negatively), getting closer and closer to zero. (For example, values like -0.00001, -0.000001 are very close to zero) • As sin x becomes smaller and smaller (negatively), the reciprocal csc x becomes larger and larger (negatively). • This is indicated by the falling portion of the csc curve between $\frac{3\pi}{2}$ and 2π. • As angle becomes closer and closer to 2π, this falling portion gets closer and closer to the vertical line through 2π. (why does this happen? The reader may write the answer in his/her own notebooks) • But it never touches that vertical line. • If it touch, it would mean that, x = 2π is a point in the csc curve. We know that, it cannot happen.

(v) Now we have a basic idea about how the 'U' shapes and 'inverted U' shapes are formed in positive side of the x axis.
• As the angle increases beyond 2π, this pattern repeats again and again.
(vi) Similar steps can be written for negative angles also. Those steps will explain the 'U' shapes and 'inverted U' shapes in the negative side of the x axis.
3. Based on the analysis of the graph, we can write:
• The output of f(x) = csc x can be any +ve real number starting from +1 and higher.
• The output of f(x) = csc x can be any -ve real number starting from -1 and lower.
• The values lying between -1 and +1 cannot be outpit values.
4. So the range of f(x) = csc is R - (-1, +1)
• That means, we have to subtract the set (-1, +1) from the the set of real numbers R
• The resulting set after subtraction is the range of f(x) = csc x
• (-1, +1) indicates that:
   ♦ all values between -1 and +1 are inculded in the set (-1, +1).
   ♦ '(' on the left side indicates that -1 is not included in the set (-1, +1).
   ♦ ')' on the right side indicates that +1 is not included in the set (-1, +1).
• So it is clear that, the two values -1 and +1 should not be subtracted from R.

---

In the next section, we will see domain and range of cosine and secant functions.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 3.7 - Input Values For Trigonometric Functions

In the previous section, we saw how the trigonometric ratios of negative angles. In this section, we will see trigonometric functions.

We have seen the basics about functions in the previous chapter-2. Let us see how that concept can be applied to trigonometric ratios. It can be written in 5 steps:
1. Consider the function f(x) = 2x + 5
• We input various values for x. Each of those input values are processed according to the function f(x) = 2x + 5
• After the processing, we get various output values. For example,
   ♦ if the input x is 3, the output f(x) will be 11    
   ♦ if the input x is 7, the output f(x) will be 19
2. Now consider sin x
• Let us input a value for x, say ${\frac{\pi}{6}}^c$
• ${\frac{\pi}{6}}^c$ is equal to $\frac{3.14}{6}$ which is equal to 0.5233
• So if we input x = 0.5233, that input value will be processed.
   ♦ After processing, we will get the sine of 0.5233, which is equal to 0.5
   ♦ (Recall that, ${\frac{\pi}{6}}^c$ = sin 30 = 0.5)
3. Let us input another value for x, say ${\frac{2\pi}{3}}^c$
• ${\frac{2\pi}{3}}^c$ is equal to $\frac{2 \times 3.14}{3}$ which is equal to 2.0933
• So if we input x = 2.0933, that input value will be processed.
   ♦ After processing, we will get the sine of 2.0933, which is equal to 0.8665
   ♦ (Recall that, ${\frac{2\pi}{3}}^c$ = sin 120 = 0.8665)
4. We see that the trigonometric ratio ‘sin x’ can process input x values. So we can write it as a function.
• We get: f(x) = sin x
5. In this way, we can write other trigonometric ratios also in the form of functions:
   ♦ f(x) = cos x
   ♦ f(x) = tan x
   ♦ f(x) = sec x
   ♦ so on . . .

---

• We have seen that trigonometric ratios can be written in the form of functions.
• So the next question arises:
For a trigonometric function, what are the possible values of input x?
• Answer is that: We can use ‘any real number’ (with a very few exceptions) as input x.
• But how is it possible to give ‘any real number’? The ray inside a circle can rotate a maximum of only 2π^c (360^o). So the maximum value of x appears to be 2π, which is 6.28. How is it possible to give values greater than 6.28?
• We can write the explanation in 10 steps:
1. We have seen how all real numbers can be placed around a unit circle. (See fig.3.9(a) of section 3.2). Now we will see how this can be achieved in practice:
2. In fig.3.24 below, a wooden wheel of radius 1 meter is pivoted at O.
• The circumference of the wheel crosses the axes at A, B, C and D.

Fig.2.24

3. Take a measuring tape graduated in meters. (Some images can be seen here)
• Place the zero of the tape at A as shown in the fig.
• Now tightly wind the tape around the wheel in the anticlockwise direction. This is indicated by the white curved arrow.
• The numbers on the tape will occupy definite positions on the circumference of the wheel. Following are some of the important positions:
   ♦ zero of the tape will be at A
   ♦ $\frac{\pi}{2}=\frac{3.14}{2}=1.57\;\text{meter}$ will be at B
   ♦ $\pi=3.14\;\text{meter}$ will be at C
   ♦ $\frac{3\pi}{2}=\frac{3\times 3.14}{2}=4.71\;\text{meter}$ will be at D
   ♦ $2\pi=2\times 3.14=6.28\;\text{meter}$ will be at A
4. The wheel is fitted with a needle pivoted at O.
   ♦ The wheel is fixed in position. It can not rotate.
   ♦ But the needle can rotate around O
5. The needle starts to rotate (in the anticlockwise direction) from O.
• So the initial reading shown by the needle will be zero.
• Starting from A, let the needle rotate by 30^o (${\frac{\pi}{6}}^c$)
Then the needle will be pointing at the $\frac{\pi}{6}=\frac{3.14}{2}=0.5233\; \text{meter}$ mark on the tape.    
• Starting from A, let the needle rotate by 120^o (${\frac{2\pi}{3}}^c$)
Then the needle will be pointing at the $\frac{2\pi}{3}=\frac{2\times 3.14}{3}=2.0933\; \text{meter}$ mark on the tape.
◼ We see that:
The angle of rotation, and the distance measured along the circumference (the arc length) are closely related.
6. When the needle completes one revolution, it will be back at A. But the reading at A now should be taken as 6.28 meter.
• After making one revolution, if the needle is rotated further, we must get readings beyond 6.28 meter. For that, we must wind the tape more than once around the wheel.
• If we assume that the thickness of the tape is infinitesimal, the radius of the wheel will be always 1 meter. With infinitesimal thickness, we can make infinite number of windings. The radius will not change.
7. Thus all the numbers on a 'tape of infinite length', will get a position on the circumference of the wheel.
• We know that numbers like π, √2, √3, √5, √7, $\frac{1}{3},\,\frac{1}{7}$ etc., are real numbers.
• All such numbers have unique positions on the tape. For example, √7 is 2.6457. . . It lies between 2 and 3. Since, 2 and 3 have unique positions on the tape, 2.6457. . . will also have a unique position on the tape.
• Thus we see that, all positive real numbers have unique positions in the tape.
• It follows that, all positive real numbers will have unique positions in the circumference of the wheel.
8. So the needle can make any number of revolutions. After those revolutions, the needle can be kept at:
   ♦ any position between A, B, C and D.
   ♦ any position exactly on A, B, C and D
• What ever be the position, we will get a unique reading on the circumference. This reading will be same as the angle of rotation x.
9. In the above steps, we rotated the needle in the anticlockwise wise direction.
• If we rotate the needle in the clockwise direction, the angles will be -ve.
• So we must get -ve readings on the circumference. This can be achieved in 3 steps:
(i) Take the same tape as before
• Place the zero of the tape at A as shown in the fig.3.25 below:

Fig.2.25

• Now tightly wind the tape around the wheel in the clockwise direction. This is indicated by the white curved arrow.
• The numbers on the tape will occupy definite positions on the circumference of the wheel.
(ii) Assume that, there is a -ve sign before every markings on the tape.
• Then some of the important positions will be as follows:
   ♦ zero of the tape will be at A
   ♦ $-{\frac{\pi}{2}}=-{\frac{3.14}{2}}=-1.57\;\text{meter}$ will be at D
   ♦ $-\pi=-3.14\;\text{meter}$ will be at C
   ♦ $-{\frac{3\pi}{2}}=-{\frac{3\times 3.14}{2}}=-4.71\;\text{meter}$ will be at B
   ♦ $-2\pi=-2\times 3.14=-6.28\;\text{meter}$ will be at A
(iii) As before, by making infinite windings of this 'negative tape' in the clockwise direction, all the negative real numbers will get unique positions on the circumference of the wheel.
10. Now the needle can make any number of revolutions in the clockwise direction. After those revolutions, it can be kept at:
   ♦ any position between A, B, C and D.
   ♦ any position exactly on A, B, C and D
• What ever be the position, we will get a unique reading on the circumference.
11. Based on the above steps, we can write:
The input x value in f(x) = sin x can be any real number.
• Like wise, for the other trigonometric functions like f(x) = cos x, f(x) = cot x etc., also, the input x can be any real number.

---

• We know that, the ratios tan x, csc x, sec x and cot x can be written in terms of sin x or cos x.
• In those ratios, either sin x or cos x comes in the denominator.
    ♦ Denominator of a fraction cannot become zero.
• So our next task is to find the situations when sin x and cos x becomes zero.

First we will see sin x. It can be written in 10 steps:
1. From the discussions in previous sections, we know that:
• sin x = 0 when the needle points towards A and C
   ♦ At A, the angle is 0
   ♦ At C, the angle is π
(Needle is rotating in the anticlockwise direction)
• So we get: sin 0 = 0 and sin π= 0
2. After reaching C, if the needle proceeds to complete one revolution, it will reach A. The sine will again become zero. In such a situation, the angle of rotation is 2π.
   ♦ So we can write: sin 2π = 0
• After completing one revolution, if the needle reaches C again, the sine will again become zero. In such a situation, the angle of rotation is (2π + π)  = 3π
   ♦ So we can write: sin 3π = 0
3. After reaching C, if the needle proceeds to complete the second revolution, it will reach A. The sine will again become zero. In such a situation, the angle of rotation is 4π.
   ♦ So we can write: sin 4π = 0
• After completing two revolution, if the needle reaches C again, the sine will again become zero. In such a situation, the angle of rotation is (4π + π)  = 5π
   ♦ So we can write: sin 5π = 0
4. We can write like this up to infinity. The angles at which sine becomes zero are: 0, π, 2π, 3π, 4π, 5π, . . .
• We see a pattern: They are all multiples of π.
   ♦ That is, π is multiplied by the numbers 1, 2, 3, 4, . . .
5. Next let us see rotation in the clockwise direction. From the discussions in previous sections, we know that:
• sin x = 0 when the needle points towards A and C
   ♦ At A, the angle is 0
   ♦ At C, the angle is -π
(Needle is rotating in the clockwise direction)
• So we get: sin 0 = 0 and sin π = 0
6. After reaching C, if the needle proceeds to complete one revolution, it will reach A. The sine will again become zero. In such a situation, the angle of rotation is -2π.
   ♦ So we can write: sin -2π = 0
• After completing one revolution, if the needle reaches C again, the sine will again become zero. In such a situation, the angle of rotation is (-2π - π)  = -3π
   ♦ So we can write: sin -3π = 0
7. After reaching C, if the needle proceeds to complete the second revolution, it will reach A. The sine will again become zero. In such a situation, the angle of rotation is -4π.
   ♦ So we can write: sin -4π = 0
• After completing two revolution, if the needle reaches C again, the sine will again become zero. In such a situation, the angle of rotation is (-4π - π)  = -5π
   ♦ So we can write: sin -5π = 0
8. We can write like this up to -ve infinity. The angles at which sine becomes zero are: 0, -π, -2π, -3π, -4π, -5π, . . .
• We see a pattern: They are all negative multiples of π.
   ♦ That is, π is multiplied by the numbers -1, -2, -3, - 4, . . .
9. Let us try to obtain a general form:
• In step (4), we got positive numbers 1, 2, 3, 4, . . .
• In step (8), we got negative odd numbers -1, -2, -3, - 4, . . .
• We have a general form which will give both positive and negative numbers:
The set of integers, n: {. . . -4, -3, -2, 1, 0, 1, 2, 3, 4, 5, . . .}
• So n will give all positive and negative integers.
• We want the general form when π is multiplied by +ve and -ve integers.
• Obviously, that general form will be: nπ,  where n is the set of integers.
10. So we can write:
sine will become zero when the angle is nπ,  where n is any integer

---

Next we will see cos x. It can be written in 10 steps:
1. From the discussions in previous sections, we know that:
• cos x = 0 when the needle points towards B and D
   ♦ At B, the angle is ${\frac{\pi}{2}}^c$
   ♦ At D, the angle is ${\frac{3\pi}{2}}^c$
(Needle is rotating in the anticlockwise direction)
• So we get: $\cos \frac{\pi}{2}=0$ and $\cos \frac{3\pi}{2}=0$
2. After completing one revolution, if the needle reaches B again, the cosine will again become zero. In such a situation, the angle of rotation is ${2\pi+\frac{\pi}{2}=\frac{5\pi}{2}}^c$
   ♦ So we can write: $\cos \frac{5\pi}{2}=0$
• After completing one revolution, if the needle reaches D again, the cosine will again become zero. In such a situation, the angle of rotation is ${2\pi+\frac{3\pi}{2}=\frac{7\pi}{2}}^c$
   ♦ So we can write: $\cos \frac{7\pi}{2}=0$
3. After completing two revolution, if the needle reaches B again, the cosine will again become zero. In such a situation, the angle of rotation is ${4\pi+\frac{\pi}{2}=\frac{9\pi}{2}}^c$
   ♦ So we can write: $\cos \frac{9\pi}{2}=0$
• After completing two revolution, if the needle reaches D again, the cosine will again become zero. In such a situation, the angle of rotation is ${4\pi+\frac{3\pi}{2}=\frac{11\pi}{2}}^c$
   ♦ So we can write: $\cos \frac{11\pi}{2}=0$
4. We can write like this up to infinity. The angles at which cosine becomes zero are:
${\frac{\pi}{2}}^c,\, {\frac{3\pi}{2}}^c,\, {\frac{5\pi}{2}}^c,\, {\frac{7\pi}{2}}^c,\, {\frac{9\pi}{2}}^c,\,.\,.\,.$
• We see a pattern: They are all odd multiples of $\frac{\pi}{2}$
   ♦ That is, $\frac{\pi}{2}$ is multiplied by the odd numbers 1, 3, 5, 7, . . .
5. Next let us see rotation in the clockwise direction. From the discussions in previous sections, we know that:
• cos x = 0 when the needle points towards D and B
   ♦ At D, the angle is $-{\frac{\pi}{2}}^c$
   ♦ At B, the angle is $-{\frac{3\pi}{2}}^c$
(Needle is rotating in the clockwise direction)
• So we get: $\cos \left(-\frac{\pi}{2}\right)=0$ and $\cos \left(-\frac{3\pi}{2}\right)=0$
6. After completing one revolution, if the needle reaches D again, the cosine will again become zero. In such a situation, the angle of rotation is ${-2\pi-\frac{\pi}{2}=-\frac{5\pi}{2}}^c$
   ♦ So we can write: $\cos \left(-\frac{5\pi}{2}\right)=0$
• After completing one revolution, if the needle reaches B again, the cosine will again become zero. In such a situation, the angle of rotation is ${-2\pi+\frac{3\pi}{2}=-\frac{7\pi}{2}}^c$
   ♦ So we can write: $\cos \left(-\frac{7\pi}{2}\right)=0$
7. After completing two revolution, if the needle reaches D again, the cosine will again become zero. In such a situation, the angle of rotation is ${-4\pi-\frac{\pi}{2}=-\frac{9\pi}{2}}^c$
   ♦ So we can write: $\cos \left(-\frac{9\pi}{2}\right)=0$
• After completing two revolution, if the needle reaches B again, the cosine will again become zero. In such a situation, the angle of rotation is ${-4\pi-\frac{3\pi}{2}=-\frac{11\pi}{2}}^c$
   ♦ So we can write: $\cos \left(-\frac{11\pi}{2}\right)=0$
8. We can write like this up to infinity. The angles at which cosine becomes zero are:
${-\frac{\pi}{2}}^c,\, {-\frac{3\pi}{2}}^c,\, {-\frac{5\pi}{2}}^c,\, {-\frac{7\pi}{2}}^c,\, {-\frac{9\pi}{2}}^c,\,.\,.\,.$
• We see a pattern: They are all negative odd multiples of $\frac{\pi}{2}$
   ♦ That is, $\frac{\pi}{2}$ is multiplied by the negative odd numbers -1, -3, -5, -7, . . .
9. Let us try to obtain a general form:
• In step (4), we got positive odd numbers 1, 3, 5, 7, . . .
• In step (8), we got negative odd numbers -1, -3, -5, -7, . . .
• In our previous classes, we have seen a general form which will give both positive and negative odd numbers:
(2n+1) where n is the set of integers: {. . . -4, -3, -2, 1, 0, 1, 2, 3, 4, 5, . . .}
• Let us see some examples:
   ♦ When n = -2, (2n+1) = -3
   ♦ When n = -1, (2n+1) = -1
   ♦ When n = 0, (2n+1) = 1
   ♦ When n = 2, (2n+1) = 5
   ♦ When n = 5, (2n+1) = 11
• So (2n+1) will give all positive and negative odd numbers when integers are put in place of n
• We want the general form when $\frac{\pi}{2}$ is multiplied by +ve and -ve odd numbers.
• Obviously, that general form will be:
$\frac{(2n+1)\pi}{2}$, where n is the set of integers.
10. So we can write:
cosine will become zero when the angle is $\frac{(2n+1)\pi}{2}$,  where n is any integer.

---

Let us write a summary of all the steps that we wrote in this section. It can be written in steps:
1. Trigonometric ratios like sin x, cos x etc., can be written as trigonometric functions: f(x) = sin x, f(x) = cos x, f(x) = sec x etc.,
2. Any real number can be used as input x for those trigonometric functions.
    ♦ There are a few exceptions. Some real numbers are not allowed
    ♦ We will see them in the next section
3. f(x) = sin x will become zero if input x is nπ,  where n is any integer.
4. f(x) = cos x will become zero if input x is $\frac{(2n+1)\pi}{2}$, where n is any integer.

---

In the next section, we will see graphs of various trigonometric functions.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 3.6 - Trigonometric Ratios of Negative Angles

In the previous section, we saw how the trigonometric ratios of any angle (acute or obtuse) can be written by applying the new method. But the angles that we saw were obtained by rotating the ray in the anticlockwise direction. When the rotation is in the anticlockwise direction, angles will be +ve. In this section, we will see rotation in the clockwise direction. When the rotation is in the clockwise direction, the angles will be negative.

In the previous section, we effectively used the new method for all positive angles. Once we are familiar with that process, we can write the trigonometric ratios of negative angles also. We will need to write only minimum steps.
1. In fig.3.21(a) below, the ray began it’s rotation from the x axis. The rotation is in the clockwise direction. So the angle is -x^c.

Fig.3.21

• From the right triangle OMP, we get:
   ♦ $\cos |x| = \frac{OM}{OP} = \frac{OM}{1} = OM = a$
   ♦ $\sin |x| = \frac{PM}{OP} = \frac{PM}{1} = PM = b$
(Note that, we are taking the absolute value of angle x. This is because, all we want is to get the lengths a and b)
• Since P is in the fourth quadrant, the coordinates are (a, -b)
   ♦ sine value is the y coordinate -b
   ♦ cosine value is the x coordinate a
• So the new method works for negative angles also.
2. In fig.3.21(b) above, the ray began it’s rotation from the x axis. The rotation is in the clockwise direction. So the angle is -x^c.
• Here ∠MOP = (180 - |x|).
• From the right triangle OMP, we get:
   ♦ $\cos (180 - |x|) = \frac{OM}{OP} = \frac{OM}{1} = OM = a$
   ♦ $\sin (180 - |x|) = \frac{PM}{OP} = \frac{PM}{1} = PM = b$
• Since P is in the third quadrant, the coordinates are (-a, -b)
   ♦ sine value is the y coordinate -b
   ♦ cosine value is the x coordinate -a
• Let us see an example. It can be written in 3 steps:
(i) Suppose that, x = -125^o
• Then ∠MOP = (180 - |-125|) = 55^o
(ii) So we get:
   ♦ a = OM = cos 55 = 0.5736
   ♦ b = PM = sin 55 = 0.8192
• So the coordinates of P are: (-0.5736, -0.8192)
(iii) We can write:
   ♦ cos(-125) = -0.5736
   ♦ sin(-125) = -0.8192
• The following screenshot from a scientific calculator confirms the result for cosine value. The reader may check the sine value also.

3. In fig.3.21(c) above, the ray began it’s rotation from the x axis. The rotation is in the clockwise direction. So the angle is -x^c.
• Here ∠MOP = (270 - |x|).
• From the right triangle OMP, we get:
   ♦ $\cos (270 - |x|) = \frac{OM}{OP} = \frac{OM}{1} = OM = a$
   ♦ $\sin (270 - |x|) = \frac{PM}{OP} = \frac{PM}{1} = PM = b$
• Since P is in the second quadrant, the coordinates are (-a, b)
   ♦ sine value is the y coordinate b
   ♦ cosine value is the x coordinate -a
4. In fig.3.21(d) above, the ray began it’s rotation from the x axis. The rotation is in the clockwise direction. So the angle is -x^c.
• Here ∠MOP = (360 - |x|).
• From the right triangle OMP, we get:
   ♦ $\cos (360 - |x|) = \frac{OM}{OP} = \frac{OM}{1} = OM = a$
   ♦ $\sin (360 - |x|) = \frac{PM}{OP} = \frac{PM}{1} = PM = b$
• Since P is in the first quadrant, the coordinates are (a, b)
   ♦ sine value is the y coordinate b
   ♦ cosine value is the x coordinate a

---

We are now in a position to write the trigonometric ratios of negative angles also. Let us see some solved examples:

Solved example 3.23
Given that cos x = $-\frac{3}{5}$ and x lies in the third quadrant. Find the values of other five trigonometric ratios.
Solution:
1. Using the given information, we can draw two items:
(i) A ray in the third quadrant
(ii) Base 'a' of triangle OMP = $\frac{3}{5}$ meter
This is shown in fig.3.22(a) below:

Fig.3.22

• Note that:
    ♦ cosine is $-\frac{3}{5}$. But we are taking the length 'a' as $+\frac{3}{5}$.
    ♦ This is because, cosine value is a coordinate value.
    ♦ From the coordinate value, we obtain the length.
        ✰ A length cannot be negative. 
2. Since it is a unit circle, OP = 1 meter
3. So we have two sides of the right triangle OMP.
• Then the third side PM = $\sqrt{1^2 - \left(\frac{3}{5} \right)^2} = \pm \frac{4}{5}$
4. Since length cannot be negative, we must take $+\frac{4}{5}$
• This third side PM is 'b'.
• Since P is in the third quadrant,
   ♦ x coordinate is negative
   ♦ y coordinate is negative
• So the coordinates (a,b) are: $\left(-\frac{3}{5},-\frac{4}{5} \right)$
5. Using the coordinates, we can write sin x and cos x:
sin x = y coordinate = $-\frac{4}{5}$
cos x = x coordinate = $-\frac{3}{5}$ (This is already given)
6. Using sin x and cos x, we can write tan x:
tan x = $\frac{\sin x}{\cos x}= \frac{-4/5}{-3/5}=\frac{4}{3}$
7. cot x = $\frac{1}{\tan x}= \frac{1}{4/3}=\frac{3}{4}$
8. csc x = $\frac{1}{\sin x}=\frac{1}{-4/5}=-\frac{5}{4}$
9. sec x = $\frac{1}{\cos x}=\frac{1}{-3/5}=-\frac{5}{3}$

Another method:
1. We have the identity: sin²x + cos²x = 1
⇒ sin²x = 1 - cos²x =  $1 - \left(\frac{3}{5} \right)^2=\frac{16}{25}$
⇒ sin x = $\pm \frac{4}{5}$
2. Here we must carefully consider the sign. Because, it is not a length. It is the sine value. Sine value can be +ve or -ve.
• Given that, P is in the third quadrant. In the third quadrant, sine is -ve.
• So we get: sin x = $-\frac{4}{5}$
3. Once we have sin x and cos x, the remaining ratios can be calculated as in the first method. Steps (6) to (9).

Solved example 3.24
Given that cot x = $-\frac{5}{12}$ and x lies in the second quadrant. Find the values of other five trigonometric ratios.
Solution:
1. Using the given information, we can draw one item:
The ray in the second quadrant.
2. The coordinates of P will be (-a,b)
    ♦ b will be the altitude of the triangle OMP
    ♦ |-a| will be the base of the triangle OMP
3. Derivation of various trigonometric ratios:
    ♦ The sine of x can be obtained from 'b' by applying the appropriate sign.
    ♦ The cosine of x can be obtained from 'a' by applying the appropriate sign.
    ♦ The cotangent of x will be $\frac{a}{b}$ after applying the proper signs.
• So our task is to find 'a' and 'b'.
• We do not have to worry about finding appropriate signs because, the quadrant is known.
4. In triangle OMP, we can write: $\frac{a}{b}=\frac{5}{12}$.
So $a=\frac{5b}{12}$.
(Note that, given cotangent (-5/12) is related to the angle x. It is negative. But here, we are taking (a/b) ratio for the triangle OMP. Sides of a triangle cannot be negative)
5. In triangle OMP, we can also write: a² + b² = 1
• Substituting for 'a', we get: $\left(\frac{5b}{12} \right)^2+b^2=1$
• From this we get: b = $\pm \frac{12}{13}$
    ♦ Since 'b' is a length, we must take: b = $+\frac{12}{13}$
• Substituting for 'b' in (4), we get: $a=\frac{5}{12} \times \frac{12}{13} = \frac{5}{13}$.
6. Thus we get the coordinates of P:
    ♦ x coordinate of P =$-\frac{5}{13}$
    ♦ y coordinate of P =$\frac{12}{13}$
7. Now we can write sine and cosine of x
    ♦ sin x = y coordinate of P = $\frac{12}{13}$
    ♦ cos x = x coordinate of P = $-\frac{5}{13}$
8. Using sin x and cos x, we can write tan x:
tan x = $\frac{\sin x}{\cos x}= \frac{12/13}{-5/13}=-\frac{12}{5}$
9. cot x = $\frac{1}{\tan x}= \frac{1}{-12/5}=-\frac{5}{12}$ (This is already given)
10. csc x = $\frac{1}{\sin x}=\frac{1}{12/13}=-\frac{13}{12}$
11. sec x = $\frac{1}{\cos x}=\frac{1}{-5/13}=-\frac{13}{5}$

Another method:
1. We have the identity: 1 + cot²x = csc²x
⇒ csc²x = $1 + \left(-\frac{5}{12} \right)^2=\frac{169}{144}$
⇒ csc x = $\pm \frac{13}{12}$
2. Here we must carefully consider the sign. Because, it is not a length. It is the csc value. csc value can be +ve or -ve.
• Given that, P is in the second quadrant. In the second quadrant, sine is +ve. So csc must also be positive.
• So we get: csc x = $+\frac{13}{12}$
3. Now we can find sine value by taking the reciprocal of the csc value. We get:
sin x = $+\frac{12}{13}$
4. Next we can find cos x using sin x and the given cot x.
• We have: cot x = $-\frac{5}{12} = \frac{\cos x}{\sin x}=\frac{\cos x}{12/13}$
• Thus we get: cos x = $-\frac{5}{12} \times \frac{12}{13}=-\frac{5}{13}$
3. Once we have sin x and cos x, the remaining ratios can be calculated as in the first method. Steps (8) to (11).

Solved example 3.25
Find the value of $\sin \frac{31\pi}{3}$
Solution:
1. First we compare $\sin \frac{31\pi}{3} ~\text{with}~ 2\pi$
• For that, we convert 2𝞹 to a fraction form with denominator '3'.
    ♦ We get: $2\pi = \frac{6\pi}{3}$
• So obviously, $\sin \frac{31\pi}{3}$ is larger than 2𝞹.
2. That means, the ray has completed more than one revolutions.
• We need to find how many revolutions were completed.
• For that we do the division: $\frac{\frac{31\pi}{3}}{2 \pi}=\frac{31}{6}=5\frac{1}{6}$
• That means, the ray first completed 5 revolutions. Then it rotated by 1/6 of a revolution
3. 1/6 of a revolution is: $\frac{1}{6} \times 2 \pi= {\frac{\pi}{3}}^c$
• So we can write:
After completing 5 revolutions, the ray rotated through ${\frac{\pi}{3}}^c$
4. ${\frac{\pi}{3}}^c$ is 60^o.
• Since the given angle is +ve, the rotations were done in the anticlockwise direction.
• After completing 5 revolutions in the anticlockwise direction, the ray further rotated by 60^o. So P is in the first quadrant. This is shown in fig.3.23(a) below:

Fig.2.23

• We want the y coordinate of P (because, y coordinate is the sine).
5. We already know the x coordinate in the following situation:
    ♦ when the ray is in the first quadrant.
    ♦ Also the ray makes 60^o with the x axis.
• The x coordinate is $\frac{\sqrt{3}}{2}$ (see fig.3.14 of section 3.4)
6. So when the ray rotates through ${\frac{\pi}{3}}^c$ in the anticlockwise direction, the final position of P will have an x coordinate of $\frac{\sqrt{3}}{2}$
• That means: $\sin \frac{31\pi}{3}=\frac{\sqrt{3}}{2}$

Solved example 3.26
Find the value of cos (-1710^o)
Solution:
1. First we compare the numerical value of -1710^o with 360^o
• Obviously, 1710 is larger than 360.
2. That means, the ray has completed more than one revolutions.
• We need to find how many revolutions were completed.
• For that we do the division: $\frac{1710}{360}=\frac{19}{4}=4\frac{3}{4}$
• That means, the ray first completed 4 revolutions. Then it rotated by 3/4 of a revolution.
3. 3/4 of a revolution is: $\frac{3}{4} \times 360= 270^o$
• So we can write:
After completing 4 revolutions, the ray rotated through 270^o
4. Since the given angle is -ve, the rotations were done in the clockwise direction.
• After completing 4 revolutions in the clockwise direction, the ray further rotated by 270^o. So P is in the +ve side of the y axis. This is shown in fig.3.23(b) above.
• We want the x coordinate of P (because, x coordinate is the cosine)
5. The x coordinate of P can be written without any difficulty because, P is exactly on the y axis. We see that, the x coordinate of P is zero.
6. So when the ray rotates through -1710^o, the final position of P will have an x coordinate of zero.
• That means: cos (-1710^o) = 0

---

Link to a few more examples are given below:

Solved examples 3.27 and 3.28

---

In the next section, we will see some basic details about trigonometric functions.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 3.5 - Trigonometric Ratios of Obtuse Angles

In the previous section, we saw the trigonometric ratios of acute angles. We also saw a new method for finding trigonometric ratios. In this section, we will see trigonometric ratios of obtuse angles.

The details can be written in steps:
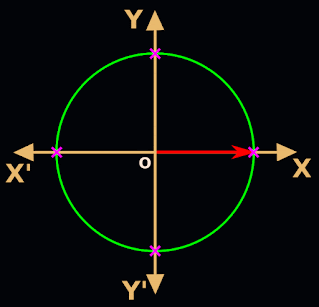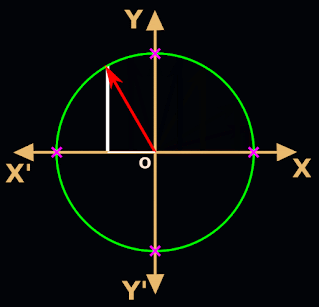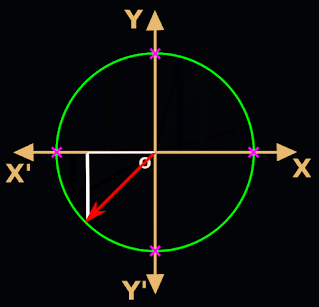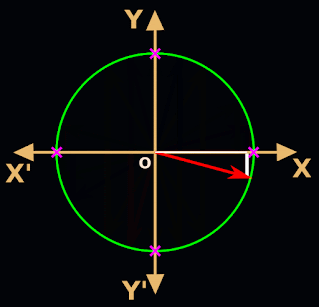
1. Recall the unit circle that we saw in the previous section.
• The ray indicated by the red arrow stopped rotation before reaching 90^o.
    ♦ So x was an acute angle.
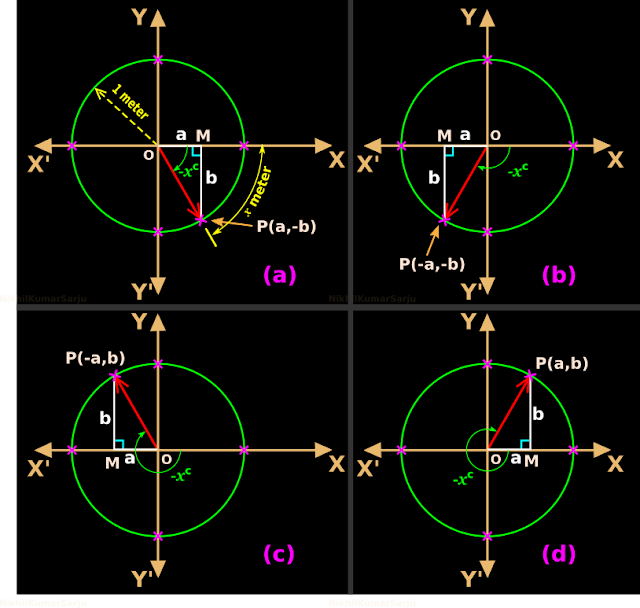
2. But for our present discussion, the ray has rotated beyond 90^o. This is shown in fig.3.17 below:

Fig.3.17

• The angle of rotation x is now greater than 90^o.
• The ray is now in the second quadrant.
3. In the traditional method, we use a right triangle to find sine and cosine.
• A right triangle will have a hypotenuse.
• So $\text{sine}=\frac{\text{opposite side}}{\text{hypotenuse}}~\text{and}~\text{cosine}=\frac{\text{adjacent side}}{\text{hypotenuse}}$.
4. But in our present case, the angle x is greater than 90^o.
• No right triangle can be drawn with one of the angle greater than 90^o. If there is no right triangle, there is no hypotenuse. So we cannot calculate sine and cosine using the traditional method.
• In such a situation, we use the new method that we saw at the end of the previous section.
5. Applying the new method to the angle x in fig.3.17 above, we get:
    ♦ sin x = y coordinate of P = b
    ♦ cos x = x coordinate of P = a
6. We can easily calculate a and b using the right triangle OMP.
Let us see an example. It can be written in 3 steps:
(i) Suppose that, x = ${\frac{5\pi}{6}}^c$ (150^o).
Then ∠MOP = (180 - 150) = 30^o
(ii) So we get:
$\begin{eqnarray}
a &=& OP \cos 30 = 1 \times \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2} \nonumber \\
b &=& OP \sin 30 = 1 \times \frac{1}{2}=\frac{1}{2} \nonumber \
\end{eqnarray}$
• Thus the coordinates of P are $\left(-\frac{\sqrt{3}}{2},\frac{1}{2} \right)$
(iii) So based on the new method, we get:
   ♦ sin 150 = y coordinate of P = $\frac{1}{2}$
   ♦ cos 150 = x coordinate of P = -$\frac{\sqrt{3}}{2}$
Another example:
(i) Suppose that, x = ${\frac{25\pi}{36}}^c$ (125^o).
• Then ∠MOP = (180 - 125) = 55^o
• 55^o is an acute angle. It's sine and cosine can be obtained from standard tables or by using a calculator.
• We have: sin 55 = 0.8192 and cos 55 = 0.5736
(ii) So we get:
a = OP cos 55 = 1 × 0.5736 = 0.5736
b = OP sin 55 = 1 × 0.8192 = 0.8192
• Thus the coordinates of P are (-0.5736, 0.8192)
(iii) So based on the new method, we get:
   ♦ sin 125 = y coordinate of P = 0.8192
   ♦ cos 125 = x coordinate of P = -0.5736
• The following screen shot from a scientific calculator confirms the result of sine value. The reader may check the cosine value also.

7. From the two examples, we can see an interesting relation. It can be written in 3 steps:
(i) In example 1, we get:
   ♦ sin 150 = $\frac{1}{2}$ = sin 30
   ♦ cos 150 = -$\frac{\sqrt{3}}{2}$ = -cos 30
(ii) In example 2, we get:
   ♦ sin 125 = 0.8192 = sin 55
   ♦ cos 125 = -0.5736 = -cos 55
(iii) Angles between 90 and 180 can be related to 180. In our present examples, 150 = (180-30) and 125 = (180-55)
• We can write:
   ♦ sin (180-30) = -$\frac{1}{2}$ = sin 30
   ♦ cos (180-30) = -$\frac{\sqrt{3}}{2}$ = -cos 30
   ♦ sin (180-55) = -0.8192 = sin 55
   ♦ cos (180-55) = -0.5736 = -cos 55
• So we can write the general form:
   ♦ sin (180-x) = sin x
   ♦ cos (180-x) = -cos x
8. Next we will find sin180 and cos 180
It can be explained in 3 steps:
(i) Suppose that, the rotation of the ray stops at such a position that, x is very close to π^c (180^o).
• For example, the rotation may stop when the angle is 179.999999^o
   ♦ Then P will be very close to C
(ii) In such a situation,
    ♦ b will be very small.
        ✰ It can be taken to be equal to zero
    ♦ a will be very close to OC
        ✰ It can be taken to be equal to OC
(iii) So we get coordinates (a,b) of P as: (-1, 0)
• An angle very close to 180^o can be taken to be equal to 180^o.
• Then we can write:
    ♦ cos 180 =  x coordinate of P = a = -1
    ♦ sin 180 = y coordinate of P = b = 0

---

9. Next we will see the case when the rotation is greater than 180^o. The following steps from (10) to (17) will give the details:
10. In fig.3.18 below, the ray has rotated beyond 180^o.

Fig.3.18

• The ray is now in the third quadrant.
11. In the traditional method, we use a right triangle to find sine and cosine.
• A right triangle will have a hypotenuse.
• So $\text{sine}=\frac{\text{opposite side}}{\text{hypotenuse}}~\text{and}~\text{cosine}=\frac{\text{adjacent side}}{\text{hypotenuse}}$.
12. But in our present case, the angle x is greater than 90^o.
• No right triangle can be drawn with one of the angle greater than 90^o. If there is no right triangle, there is no hypotenuse. So we cannot calculate sine and cosine using the traditional method.
• In such a situation, we use the new method that we saw at the end of the previous section.
13. Applying the new method to the angle x in fig.3.16 above, we get:
    ♦ sin x = y coordinate of P = b
    ♦ cos x = x coordinate of P = a
14. We can easily calculate a and b using the right triangle OMP.
Let us see an example. It can be written in 3 steps:
(i) Suppose that, x = ${\frac{7\pi}{6}}^c$ (210^o).
Then ∠MOP = (210 - 180) = 30^o
(ii) So we get:
$\begin{eqnarray}
a &=& OP \cos 30 = 1 \times \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2} \nonumber \\
b &=& OP \sin 30 = 1 \times \frac{1}{2}=\frac{1}{2} \nonumber \
\end{eqnarray}$
• Thus the coordinates of P are $\left(-\frac{\sqrt{3}}{2},-\frac{1}{2} \right)$
(iii) So based on the new method, we get:
sin 210 = y coordinate of P = -$\frac{1}{2}$
cos 210 = x coordinate of P = -$\frac{\sqrt{3}}{2}$
Another example:
(i) Suppose that, x = ${\frac{47\pi}{36}}^c$ (235^o).
Then angleMOP = (235 - 180) = 55^o
55^o is an acute angle. it's sine and cosine can be obtained from standard tables or by using a calculator.
We have: sin 55 = 0.8192 and cos 55 = 0.5736
(ii) So we get:
a = OP cos 55 = 1 × 0.5736 = 0.5736
b = OP sin 55 = 1 × 0.8192 = 0.8192
• Thus the coordinates of P are (-0.5736, -0.8192)
(iii) So based on the new method, we get:
sin 235 = y coordinate of P = -0.8192
cos 235 = x coordinate of P = -0.5736
16. From the two examples, we can see an interesting relation. It can be written in 3 steps:
(i) In example 1, we get:
   ♦ sin 210 = -$\frac{1}{2}$ = -sin 30
   ♦ cos 210 = -$\frac{\sqrt{3}}{2}$ = -cos 30
(ii) In example 2, we get:
   ♦ sin 235 = -0.8192 = -sin 55
   ♦ cos 235 = -0.5736 = -cos 55
(iii) Angles between 180 and 270 can be related to 180. In our present examples, 210 = (180+30) and 235 = (180+55)
• We can write:
   ♦ sin (180+30) = -$\frac{1}{2}$ = -sin 30
   ♦ cos (180+30) = -$\frac{\sqrt{3}}{2}$ = -cos 30
   ♦ sin (180+55) = -0.8192 = -sin 55
   ♦ cos (180+55) = -0.5736 = -cos 55
• So we can write the general form:
   ♦ sin (180+x) = -sin x
   ♦ cos (180+x) = -cos x
17. Next we will find sin 270 and cos 270
It can be explained in steps:
(i) Suppose that, the rotation of the ray stops at such a position that, x is very close to ${\frac{3\pi}{2}}^c$ (270^o).
• For example, the rotation may stop when the angle is 269.999999^o
   ♦ Then P will be very close to D
(ii) In such a situation,
    ♦ a will be very small.
        ✰ It can be taken to be equal to zero
    ♦ b will be very close to OD
        ✰ It can be taken to be equal to OD
(iii) So we get coordinates (a,b) of P as: (0,-1)
• An angle very close to 270^o can be taken to be equal to 270^o.
• Then we can write:
    ♦ cos 270 =  x coordinate of P = a = 0
    ♦ sin 270 = y coordinate of P = b = -1

---

18. Next we will see the case when the rotation is greater than 270^o. The following steps from (19) to (24) will give the details:
19. In fig.3.19 below, the ray has rotated beyond 270^o.

Fig.3.19

• The ray is now in the fourth quadrant.
20. As before, here also, we cannot use the traditional method because, the angle is greater than 90^o. So we apply the new method using coordinates (a,b).
21. Applying the new method to the angle x in fig.3.19 above, we get:
    ♦ sin x = y coordinate of P = b
    ♦ cos x = x coordinate of P = a
22. We can easily calculate a and b using the right triangle OMP.
Let us see an example. It can be written in 3 steps:
(i) Suppose that, x = ${\frac{5\pi}{3}}^c$ (300^o).
• Then ∠MOP = (300 - 270) = 30^o
(ii) So we get:
$\begin{eqnarray}
a &=& OP \cos 30 = 1 \times \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2} \nonumber \\
b &=& OP \sin 30 = 1 \times \frac{1}{2}=\frac{1}{2} \nonumber \
\end{eqnarray}$
• Thus the coordinates of P are $\left(\frac{\sqrt{3}}{2},-\frac{1}{2} \right)$
(iii) So based on the new method, we get:
   ♦ sin 300 = y coordinate of P = $\frac{1}{2}$
   ♦ cos 300 = x coordinate of P = -$\frac{\sqrt{3}}{2}$
Another example:
(i) Suppose that, x = ${\frac{65\pi}{36}}^c$ (325^o).
• Then ∠MOP = (325 - 270) = 55^o
• 55^o is an acute angle. it's sine and cosine can be obtained from standard tables or by using a calculator.
• We have: sin 55 = 0.8192 and cos 55 = 0.5736
(ii) So we get:
a = OP cos 55 = 1 × 0.5736 = 0.5736
b = OP sin 55 = 1 × 0.8192 = 0.8192
• Thus the coordinates of P are (0.5736, -0.8192)
(iii) So based on the new method, we get:
sin 235 = y coordinate of P = -0.8192
cos 235 = x coordinate of P = 0.5736
23. From the two examples, we can see an interesting relation. It can be written in 3 steps:
(i) In example 1, we get:
   ♦ sin 300 = -$\frac{1}{2}$ = -sin 30
   ♦ cos 300 = -$\frac{\sqrt{3}}{2}$ = -cos 30
(ii) In example 2, we get:
   ♦ sin 325 = -0.8192 = -sin 55
   ♦ cos 325 = 0.5736 = cos 55
(iii) Angles between 270 and 360 can be related to 270. In our present examples, 300 = (270+30) and 325 = (270+55)
• We can write:
   ♦ sin (270+30) = -$\frac{1}{2}$ = -sin 30
   ♦ cos (270+30) = $\frac{\sqrt{3}}{2}$ = cos 30
   ♦ sin (270+55) = -0.8192 = -sin 55
   ♦ cos (270+55) = 0.5736 = cos 55
• So we can write the general form:
   ♦ sin (270+x) = -sin x
   ♦ cos (270+x) = cos x
24. Next we will find sin 360 and cos 360
It can be explained in steps:
(i) Suppose that, the rotation of the ray stops at such a position that, x is very close to ${2\pi}}^c$ (360^o).
• For example, the rotation may stop when the angle is 359.999999^o
   ♦ Then P will be very close to A
(ii) In such a situation,
    ♦ b will be very small.
        ✰ It can be taken to be equal to zero
    ♦ a will be very close to OA
        ✰ It can be taken to be equal to OA
(iii) So we get coordinates (a,b) of P as: (1,0)
• An angle very close to 360^o can be taken to be equal to 360^o.
• Then we can write:
    ♦ cos 360 =  x coordinate of P = a = 1
    ♦ sin 360 = y coordinate of P = b = 0

---

25. Next we will see the case when the rotation is greater than 360^o. The following steps from (26) to (32) will give the details:
26. In fig.3.20 below, the ray has rotated beyond 360^o.

Fig.3.20

• The ray is now back in the first quadrant.
27. We see that, the ray is now in a position that we saw in the previous section.
• So we can use either the traditional method or the new method.
• Whatever be the method,
   ♦ The result will be same as that obtained for an acute angle.
• This can be explained in 3 steps:
(i) Suppose that, the ray starts from the x axis and rotates through an angle x₁^c where x₁ is less than ${\frac{\pi}{2}}^c$
We can easily calculate a and b
(ii) Suppose that, the ray starts from the x axis, rotate through 2π (360^o) and further rotate through the same x₁ as in (i).
Here also, we can easily calculate a and b.
(iii) We can compare the results:
   ♦ The a and b calculated in (ii)
   ♦ will be exactly same as
   ♦ The a and b calculated in (i)
28. So we can write:
   ♦ sin x = sin (2π+x₁) = sin x₁
   ♦ cos x = cos (2π+x₁) = cos x₁
         ✰ Where x = (2π+x₁)  and x₁ is an acute angle.
29. In the fig.3.20, the ray completed one revolution and then further rotated through x₁. So the angle of rotation x = (2π+x₁).
We wrote:
   ♦ sin x = sin (2π+x₁) = sin x₁
   ♦ cos x = cos (2π+x₁) = cos x₁
         ✰ Where x = (2π+x₁)  and x₁ is an acute angle.
30. In some cases, the ray may complete two revolutions and then further rotate through x₁. Then the angle of rotation x will be (2 × 2π+x₁)
• We can write:
   ♦ sin x = sin (2 × 2π+x₁) = sin x₁
   ♦ cos x = cos (2 × 2π+x₁) = cos x₁
         ✰ Where x = (2 × 2π+x₁)  and x₁ is an acute angle.
• We see that, the sine and cosine values do not change.
31. In some cases, the ray may complete three revolutions and then further rotate through x₁. Then the angle of rotation x will be (3 × 2π+x₁)
• We can write:
   ♦ sin x = sin (3 × 2π+x₁) = sin x₁
   ♦ cos x = cos (3 × 2π+x₁) = cos x₁
         ✰ Where x = (3 × 2π+x₁)  and x₁ is an acute angle.
• We see that, the sine and cosine values do not change.
32. In general, the ray may complete n revolutions and then further rotate through x₁. Then the angle of rotation x will be (n × 2π+x₁)
• We can write:
   ♦ sin x = sin (2nπ+x₁) = sin x₁
   ♦ cos x = cos (2nπ+x₁) = cos x₁
         ✰ Where x = (2nπ+x₁)  and x₁ is an acute angle.
• The sine and cosine values will not change.

---

• We have seen 32 steps in this section. Those steps are related to obtuse angles.
• We have seen 31 steps in the previous section. Those steps are related to acute angles.
• Based on all those steps, we can write four points:
1. When the ray rotates in the anticlockwise direction, we are able to find the sine and cosine of any given x^c.
• All we need to do is, apply the following two steps:
(i) Find the base ‘a’ and altitude ‘b’ of the triangle OMP.
(ii) Using the base and altitude, write the coordinates of point P.
   ♦ The x coordinate will be the cosine of that angle.
   ♦ The y coordinate will be the sine of that angle.
2. We can write the signs also:
• When the ray is in the first quadrant,
   ♦ sine will be +ve
   ♦ cosine will be +ve
• When the ray is in the second quadrant,
   ♦ sine will be +ve
   ♦ cosine will be -ve
• When the ray is in the third quadrant,
   ♦ sine will be -ve
   ♦ cosine will be -ve
• When the ray is in the fourth quadrant,
   ♦ sine will be -ve
   ♦ cosine will be +ve
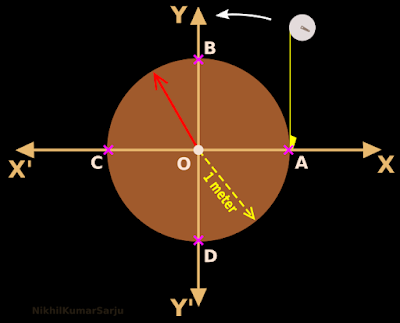
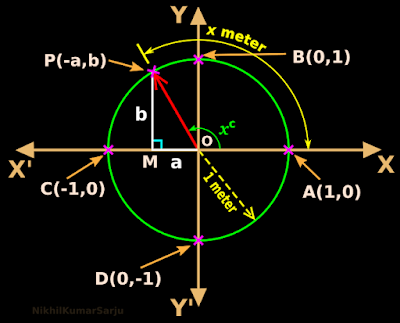
3. We can write the sine and cosine at the points A, B, C and D where the unit circle cuts the axes:
• The unit circle cuts the +ve side of the x axis at A.
   ♦ At A, x = 0^c
   ♦ sin 0 = 0, cos 0 = 1
• The unit circle cuts the +ve side of the y axis at B.
   ♦ At B, x = ${\frac{\pi}{2}}^c$
   ♦ sin $\frac{\pi}{2}$ = 1, cos $\frac{\pi}{2}$ = 0
• The unit circle cuts the -ve side of the x axis at C.
   ♦ At C, x = π^c
   ♦ sin π = 0, cos π = -1
• The unit circle cuts the -ve side of the y axis at D.
   ♦ At D, x = ${\frac{3\pi}{2}}^c$
   ♦ sin $\frac{3\pi}{2}$ = -1, cos $\frac{3\pi}{2}$ = 0
• The ray completes one revolution and returns to A
   ♦ Then at A, x = 2π^c
   ♦ sin 2π = 0, cos 2π = 1
4. From step 7(iii) below fig.3.17 at the beginning of this section, we get two useful results:
   ♦ sin (180-x) = sin x
   ♦ cos (180-x) = -cos x

---

We have completed a discussion on trigonometric ratios when the ray rotates in the anticlockwise direction. In the next section, we will see clockwise rotation.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com