In the previous section, we saw the domain and range of sine and cosecant functions. In this section, we will see the domain and range of cosine and secant functions.
Let us find the domain and range of f(x) = cos x. It can be written in 2 steps:
1. First we will find the domain:
• We have seen that:
In the case of f(x) = cos x, any real number can be used as input x.
• So we can write: Domain of f(x) = cos x, is the set R.
(Recall that, R is the set of real numbers)
2. Let us find the range of f(x) = cos x
• The range in this case can be better understood if we analyze the graph of f(x) = cos x. It is shown in fig.3.29 below:
 |
| Fig.3.29 |
• The graph of f(x) = sin x, which we saw in the previous section, is given again below. This is for a comparison.
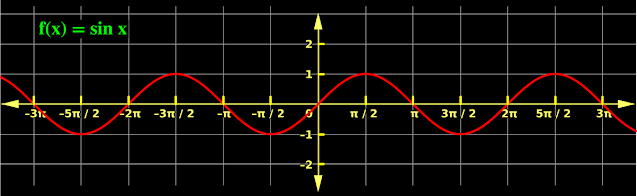 |
| Fig.3.26 |
• An analysis of the cosine graph can be written in 3 steps:
(i)
We already know the reason for the markings $\frac{\pi}{2},\; \pi,\;
\frac{3\pi}{2},\; 2\pi,\; \frac{5\pi}{2}$ so on . . . on the x axis.
(ii) Now let us consider the output y values.
• We see that, whatever be the value of input x,
♦ Output y value (that is., cosine of x) never becomes greater than 1
♦ Output y value never becomes lesser than -1
(iii)
We can mark any point on the red curve in the graph. The y coordinate
of that point will be either 1 or -1 or a value between 1 and -1.
◼ So the range can be written as [-1, 1]
• That means:
♦ All real values between -1 and 1 are included in the range.
♦ Left side '[' indicates that -1 is also included in the range.
♦ Right side ']' indicates that +1 is also included in the range.
• We just saw that, cosine value can never rise above -1. Neither can it fall below -1.
• The reason can be written in 8 steps:
1.
In the animation in fig.3.30 below, the thick white horizontal line is
the base of the triangle in our familiar unit circle.
 |
| Fig.3.30 |
2. The red ray starts to rotate from the +ve side of the x axis.
• Since the green circle is a unit circle, the length of the horizontal white line at this initial point will be 1
• As the rotation proceeds, the length of the horizontal line gradually decreases.
• It becomes zero when the ray completes a rotation of ${\frac{\pi}{2}}^c$. That is, when the ray coincides with the y axis.
• So we can write:
(i) The cosine value start to decrease from 1 (when the ray coincides with the +ve side of x axis)
(ii) The cosine value attains a value of 0 (when the ray coincides with the +ve side of y axis)
(iii) This decrease of cosine value, from 1 to zero, is indicated by the falling portion between x = 0 and x = $\frac{\pi}{2}$ in the graph in fig.3.29 above.
3. Next, the red ray proceeds to rotate from x = $\frac{\pi}{2}$ to x = π.
• We see that, the length of the horizontal white line increases from zero to 1.
• Though it is an 'increase in length', it happens on the negative side of the x axis. On this negative side, every x coordinate is negative, That means, on the negative side of the x axis, every cosine value is negative.
• As the length increases, the negative value increases. So in effect, it is a decrease.
• This decrease is indicated by the falling portion between x = $\frac{\pi}{2}$ and x = π in the graph in fig.3.29 above.
4. Next, the red ray proceeds to rotate from x = π to x = $\frac{3\pi}{2}$.
• We see that, the length of the horizontal white line decreases from 1 to zero.
• Though it is a 'decrease in length', it happens on the negative side of the x axis. On this negative side, every x values is negative, That means, on the negative side of the x axis, every cosine value is negative.
• As the length decreases, the negative value decreases. So in effect, it is an increase.
• This increase is indicated by the rising portion between x = π and x = $\frac{3\pi}{2}$ in the graph in fig.3.29 above.
5. Next, the red ray proceeds to rotate from x = $\frac{3\pi}{2}$ to x = 2π.
• We see that, the length of the horizontal white line increases from zero to 1.
• This increase is indicated by the rising portion between x = $\frac{3\pi}{2}$ and x = 2π in the graph in fig.3.29 above.
6. As the ray continues to rotate, this pattern repeats again and again. Thus we get the wave form on the positive side of the x axis in the graph.
7. Similar steps can be written for rotation in the anticlockwise direction also. Based on those steps, we will be able to explain the wave form on the negative side of the x axis in the graph.
8. Note that:
• In the first ${\frac{\pi}{2}}^c$ rotation in the anticlockwise direction, there is a fall in cosine value.
• In the first ${\frac{\pi}{2}}^c$ rotation in the clockwise direction also, there is a fall in cosine value.
• So there is a smooth transition between the two waves on either sides of the x axis.
Let us find the domain and range of f(x) = sec x. It can be written in 4 steps:
1. First we will find the domain:
• We have seen that:
♦ In the case of f(x) = sec x,
♦ $\frac{(2n+1)\pi}{2}$ where n is any integer, should not be used as input x
• So we can write:
Domain of f(x) = sec x is $R-\{x:x=\frac{(2n+1)\pi}{2},\; n\, \in \,Z\}$
• That means, we must subtract the set $\{x:x=\frac{(2n+1)\pi}{2},\; n\, \in \,Z\}$ from R. The resulting set after subtraction, is the domain of f(x) = sec x
• $\{x:x=\frac{(2n+1)\pi}{2},\; n\, \in \,Z\}$ is the set containing all $\frac{(2n+1)\pi}{2}$, where n is any integer.
2. Let us find the range of f(x) = sec x
• The range in this case can be better understood if we analyze the graph of f(x) = cos x and f(x) = sec x together. It is shown in fig.3.31 below:
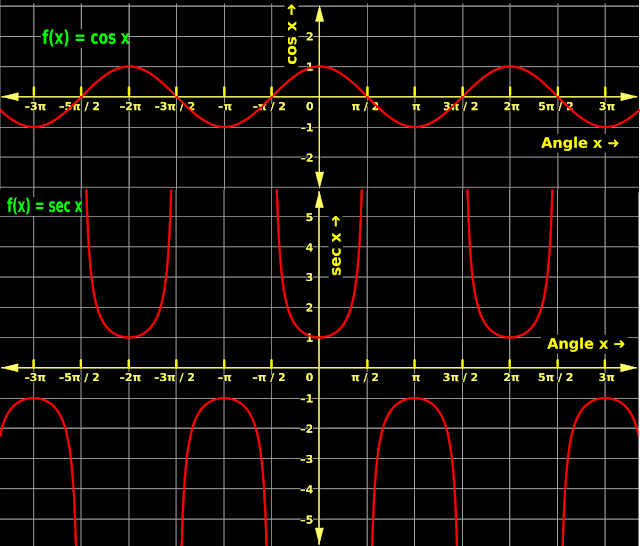 |
| Fig.3.31 |
An analysis of this graph can be written in 6 steps:
(i) Consider the segment from 0 to $\frac{\pi}{2}$ on the x axis.
• In this segment,
♦ the cosine curve falls
♦ but the secant curve rises.
• That means, when the angle increases from 0 to $\frac{\pi}{2}$,
♦ the cosine value decreases
♦ but the secant value increases.
• This is obvious because, secant is the reciprocal of cosine.
• In the segment from 0 to $\frac{\pi}{2}$, the maximum value of cosine occurs at zero
♦ So the minimum value of secant should also be at zero.
♦ Indeed we see that, the rise of the secant curve occurs after zero.
• The value of cosine at zero is 1
♦ The value of secant at zero should be the reciprocal of 1, which is 1.
♦ Indeed we see that, the value of secant at zero is 1.
• The value of cosine at $\frac{\pi}{2}$ is 0
♦ The value of secant at $\frac{\pi}{2}$ should be the reciprocal of 0, which is not defined
♦ Indeed we see that, the value of secant curve never touches the vertical line through $\frac{\pi}{2}$
• As the angle approaches $\frac{\pi}{2}$, the cosine value becomes very small and consequently the secant which is the reciprocal, becomes very large.
| ◼ As seen before, we cannot put x = $\frac{\pi}{2}$ in $f(x) = \sec x = \frac{1}{\cos x}$. We can write: • As x approaches $\frac{\pi}{2}$, cos x becomes smaller and smaller, getting closer and closer to zero. (For example, values like 0.00001, 0.000001 are very close to zero) • As cos x becomes smaller and smaller, the reciprocal sec x becomes larger and larger. • This is indicated by the rising portion of the secant curve between 0 and $\frac{\pi}{2}$. • As angle becomes closer and closer to $\frac{\pi}{2}$, this rising portion gets closer and closer to the vertical line through $\frac{\pi}{2}$. (why does this happen? The reader may write the answer in his/her own notebooks) • But it never touches that vertical line. • If it touch, it would mean that, x = $\frac{\pi}{2}$ is a point in the secant curve. We know that, it cannot happen. |
(ii) Consider the segment from $\frac{\pi}{2}$ to π on the x axis.
• In this segment,
♦ the cosine curve falls
♦ but the secant curve rises.
• That means, when the angle increases from $\frac{\pi}{2}$ to π,
♦ the cosine value decreases (increases negatively)
♦ but the secant value increases (decreases negatively).
• This is obvious because, secant is the reciprocal of cosine
Note that here, all the cosine values are -ve. Consequently, all the secant values will also be -ve.
• In the segment from $\frac{\pi}{2}$ to π, the minimum value of cosine occurs at π.
♦ So the maximum value of secant should also be at π.
♦ Indeed we see that, at π, the secant is at it's peak point in this segment.
♦ The value is reciprocal of -1, which is -1
(iii) Consider the segment from π to $\frac{3\pi}{2}$ on the x axis.
• In this segment,
♦ the cosine curve rises
♦ but the secant curve falls.
• That means, when the angle increases from π to $\frac{3\pi}{2}$,
♦ the cosine value increases
♦ but the secant value decreases.
• This is obvious because, secant is the reciprocal of cosine.
Note that here, all the cosine values are -ve. Consequently, all the secant values will also be -ve.
• In the segment from π to $\frac{3\pi}{2}$, the maximum value of cosine occurs at $\frac{3\pi}{2}$.
♦ So the minimum value of secant should also be at $\frac{3\pi}{2}$.
♦ Indeed we see that, as the angle approaches $\frac{3\pi}{2}$, the secant curve goes further and further down.
| ◼ As seen before, we cannot put x = $\frac{3\pi}{2}$ in $f(x) = \sec x = \frac{1}{\cos x}$. We can write: • As x approaches $\frac{3\pi}{2}$, cos x becomes smaller and smaller (negatively), getting closer and closer to zero. (For example, values like -0.00001, -0.000001 are very close to zero) • As cos x becomes smaller and smaller, the reciprocal sec x becomes larger and larger (negatively). • This is indicated by the falling portion of the secant curve between π and $\frac{3\pi}{2}$. • As angle becomes closer and closer to $\frac{3\pi}{2}$, this falling portion gets closer and closer to the vertical line through $\frac{3\pi}{2}$. (why does this happen? The reader may write the answer in his/her own notebooks) • But it never touches that vertical line. • If it touch, it would mean that, x = $\frac{3\pi}{2}$ is a point in the secant curve. We know that, it cannot happen. |
(iv) Consider the segment from $\frac{3\pi}{2}$ to 2π on the x axis.
• In this segment,
♦ the cosine curve rises
♦ but the secant curve falls.
• That means, when the angle increases from $\frac{3\pi}{2}$ to 2π,
♦ the cosine value increases
♦ but the secant value decreases.
• This is obvious because, secant is the reciprocal of cosine.
Note that here, all the cosine values are +ve. Consequently, all the secant values will also be +ve.
As the angle increases beyond 2π, this pattern repeats again and again.
(vi) Similar steps can be written for negative angles also. Those steps will explain the 'U' shapes and 'inverted U' shapes in the negative side of the x axis.
3. Based on the analysis of the graph, we can write:
• The output of f(x) = sec x can be any +ve real number starting from +1 and higher.
• The output of f(x) = sec x can be any -ve real number starting from -1 and lower.
• The values lying between -1 and +1 cannot be output values.
4. So the range of f(x) = sec is R - (-1, +1)
• That means, we have to subtract the set (-1, +1) from the the set of real numbers R
• The resulting set after subtraction is the range of f(x) = sec x
• (-1, +1) indicates that:
♦ all values between -1 and +1 are included in the set.
♦ '(' on the left side indicates that -1 is not included in the set.
♦ ')' on the right side indicates that +1 is not included in the set.
• So it is clear that, the two values -1 and +1 should not be subtracted from R.
In
the next
section, we will see domain and range of tangent and cotangent functions.
Previous
Contents
Next
Copyright©2021 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment