In the previous section, we saw how the trigonometric ratios of negative angles. In this section, we will see trigonometric functions.
We have seen the basics about functions in the previous chapter-2. Let us see how that concept can be applied to trigonometric ratios. It can be written in 5 steps:
1. Consider the function f(x) = 2x + 5
• We input various values for x. Each of those input values are processed according to the function f(x) = 2x + 5
• After the processing, we get various output values. For example,
♦ if the input x is 3, the output f(x) will be 11
♦ if the input x is 7, the output f(x) will be 19
2. Now consider sin x
• Let us input a value for x, say ${\frac{\pi}{6}}^c$
• ${\frac{\pi}{6}}^c$ is equal to $\frac{3.14}{6}$ which is equal to 0.5233
• So if we input x = 0.5233, that input value will be processed.
♦ After processing, we will get the sine of 0.5233, which is equal to 0.5
♦ (Recall that, ${\frac{\pi}{6}}^c$ = sin 30 = 0.5)
3. Let us input another value for x, say ${\frac{2\pi}{3}}^c$
• ${\frac{2\pi}{3}}^c$ is equal to $\frac{2 \times 3.14}{3}$ which is equal to 2.0933
• So if we input x = 2.0933, that input value will be processed.
♦ After processing, we will get the sine of 2.0933, which is equal to 0.8665
♦ (Recall that, ${\frac{2\pi}{3}}^c$ = sin 120 = 0.8665)
4. We see that the trigonometric ratio ‘sin x’ can process input x values. So we can write it as a function.
• We get: f(x) = sin x
5. In this way, we can write other trigonometric ratios also in the form of functions:
♦ f(x) = cos x
♦ f(x) = tan x
♦ f(x) = sec x
♦ so on . . .
• We have seen that trigonometric ratios can be written in the form of functions.
• So the next question arises:
For a trigonometric function, what are the possible values of input x?
• Answer is that: We can use ‘any real number’ (with a very few exceptions) as input x.
• But how is it possible to give ‘any real number’? The ray inside a circle can rotate a maximum of only 2πc (360o). So the maximum value of x appears to be 2π, which is 6.28. How is it possible to give values greater than 6.28?
• We can write the explanation in 10 steps:
1. We have seen how all real numbers can be placed around a unit circle. (See fig.3.9(a) of section 3.2). Now we will see how this can be achieved in practice:
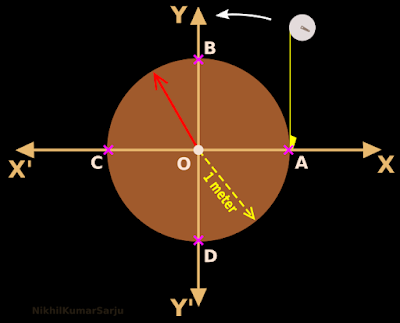
2. In fig.3.24 below, a wooden wheel of radius 1 meter is pivoted at O.
• The circumference of the wheel crosses the axes at A, B, C and D.
 |
| Fig.2.24 |
3. Take a measuring tape graduated in meters. (Some images can be seen here)
• Place the zero of the tape at A as shown in the fig.
• Now tightly wind the tape around the wheel in the anticlockwise direction. This is indicated by the white curved arrow.
• The numbers on the tape will occupy definite positions on the circumference of the wheel. Following are some of the important positions:
♦ zero of the tape will be at A
♦ $\frac{\pi}{2}=\frac{3.14}{2}=1.57\;\text{meter}$ will be at B
♦ $\pi=3.14\;\text{meter}$ will be at C
♦ $\frac{3\pi}{2}=\frac{3\times 3.14}{2}=4.71\;\text{meter}$ will be at D
♦ $2\pi=2\times 3.14=6.28\;\text{meter}$ will be at A
4. The wheel is fitted with a needle pivoted at O.
♦ The wheel is fixed in position. It can not rotate.
♦ But the needle can rotate around O
5. The needle starts to rotate (in the anticlockwise direction) from O.
• So the initial reading shown by the needle will be zero.
• Starting from A, let the needle rotate by 30o (${\frac{\pi}{6}}^c$)
Then the needle will be pointing at the $\frac{\pi}{6}=\frac{3.14}{2}=0.5233\; \text{meter}$ mark on the tape.
• Starting from A, let the needle rotate by 120o (${\frac{2\pi}{3}}^c$)
Then the needle will be pointing at the $\frac{2\pi}{3}=\frac{2\times 3.14}{3}=2.0933\; \text{meter}$ mark on the tape.
◼ We see that:
The angle of rotation, and the distance measured along the circumference (the arc length) are closely related.
6. When the needle completes one revolution, it will be back at A. But the reading at A now should be taken as 6.28 meter.
• After making one revolution, if the needle is rotated further, we must get readings beyond 6.28 meter. For that, we must wind the tape more than once around the wheel.
• If we assume that the thickness of the tape is infinitesimal, the radius of the wheel will be always 1 meter. With infinitesimal thickness, we can make infinite number of windings. The radius will not change.
7. Thus all the numbers on a 'tape of infinite length', will get a position on the circumference of the wheel.
• We know that numbers like π, √2, √3, √5, √7, $\frac{1}{3},\,\frac{1}{7}$ etc., are real numbers.
• All such numbers have unique positions on the tape. For example, √7 is 2.6457. . . It lies between 2 and 3. Since, 2 and 3 have unique positions on the tape, 2.6457. . . will also have a unique position on the tape.
• Thus we see that, all positive real numbers have unique positions in the tape.
• It follows that, all positive real numbers will have unique positions in the circumference of the wheel.
8. So the needle can make any number of revolutions. After those revolutions, the needle can be kept at:
♦ any position between A, B, C and D.
♦ any position exactly on A, B, C and D
• What ever be the position, we will get a unique reading on the circumference. This reading will be same as the angle of rotation x.
9. In the above steps, we rotated the needle in the anticlockwise wise direction.
• If we rotate the needle in the clockwise direction, the angles will be -ve.
• So we must get -ve readings on the circumference. This can be achieved in 3 steps:
(i) Take the same tape as before
• Place the zero of the tape at A as shown in the fig.3.25 below:
 |
| Fig.2.25 |
• Now tightly wind the tape around the wheel in the clockwise direction. This is indicated by the white curved arrow.
• The
numbers on the tape will occupy definite positions on the circumference
of the wheel.
(ii) Assume that, there is a -ve sign before every markings on the tape.
• Then some of the important positions will be as follows:
♦ zero of the tape will be at A
♦ $-{\frac{\pi}{2}}=-{\frac{3.14}{2}}=-1.57\;\text{meter}$ will be at D
♦ $-\pi=-3.14\;\text{meter}$ will be at C
♦ $-{\frac{3\pi}{2}}=-{\frac{3\times 3.14}{2}}=-4.71\;\text{meter}$ will be at B
♦ $-2\pi=-2\times 3.14=-6.28\;\text{meter}$ will be at A
(iii) As before, by making infinite windings of this 'negative tape' in the clockwise direction, all the negative real numbers will get unique positions on the circumference of the wheel.
10. Now the needle can make any number of revolutions in the clockwise direction. After those revolutions, it can be kept at:
♦ any position between A, B, C and D.
♦ any position exactly on A, B, C and D
• What ever be the position, we will get a unique reading on the circumference.
11. Based on the above steps, we can write:
The input x value in f(x) = sin x can be any real number.
• Like wise, for the other trigonometric functions like f(x) = cos x, f(x) = cot x etc., also, the input x can be any real number.
• We know that, the ratios tan x, csc x, sec x and cot x can be written in terms of sin x or cos x.
• In those ratios, either sin x or cos x comes in the denominator.
♦ Denominator of a fraction cannot become zero.
• So our next task is to find the situations when sin x and cos x becomes zero.
First we will see sin x. It can be written in 10 steps:
1. From the discussions in previous sections, we know that:
• sin x = 0 when the needle points towards A and C
♦ At A, the angle is 0
♦ At C, the angle is π
(Needle is rotating in the anticlockwise direction)
• So we get: sin 0 = 0 and sin π= 0
2.
After reaching C, if the needle proceeds to complete one revolution, it will reach A. The sine will again become zero. In such a situation, the angle of rotation
is 2π.
♦ So we can write: sin 2π = 0
• After completing one revolution, if the needle reaches C again, the sine
will again become zero. In such a situation, the angle of rotation is (2π + π) = 3π
♦ So we can write: sin 3π = 0
3. After reaching C, if the needle proceeds to complete the second revolution, it will reach A. The sine will again become zero. In such a situation, the angle of rotation
is 4π.
♦ So we can write: sin 4π = 0
• After completing two revolution, if the needle reaches C again, the sine
will again become zero. In such a situation, the angle of rotation is (4π + π) = 5π
♦ So we can write: sin 5π = 0
4. We can write like this up to infinity. The angles at which sine becomes zero are: 0, π, 2π, 3π, 4π, 5π, . . .
• We see a pattern: They are all multiples of π.
♦ That is, π is multiplied by the numbers 1, 2, 3, 4, . . .
5. Next let us see rotation in the clockwise direction. From the discussions in previous sections, we know that:
• sin x = 0 when the needle points towards A and C
♦ At A, the angle is 0
♦ At C, the angle is -π
(Needle is rotating in the clockwise direction)
• So we get: sin 0 = 0 and sin π = 0
6.
After reaching C, if the needle proceeds to complete one revolution, it
will reach A. The sine will again become zero. In such a situation, the
angle of rotation
is -2π.
♦ So we can write: sin -2π = 0
• After completing one revolution, if the needle reaches C again, the sine
will again become zero. In such a situation, the angle of rotation is (-2π - π) = -3π
♦ So we can write: sin -3π = 0
7.
After reaching C, if the needle proceeds to complete the second
revolution, it will reach A. The sine will again become zero. In such a
situation, the angle of rotation
is -4π.
♦ So we can write: sin -4π = 0
• After completing two revolution, if the needle reaches C again, the sine
will again become zero. In such a situation, the angle of rotation is (-4π - π) = -5π
♦ So we can write: sin -5π = 0
8. We can write like this up to -ve infinity. The angles at which sine becomes zero are: 0, -π, -2π, -3π, -4π, -5π, . . .
• We see a pattern: They are all negative multiples of π.
♦ That is, π is multiplied by the numbers -1, -2, -3, - 4, . . .
9. Let us try to obtain a general form:
• In step (4), we got positive numbers 1, 2, 3, 4, . . .
• In step (8), we got negative odd numbers -1, -2, -3, - 4, . . .
• We have a general form which will give both positive and negative numbers:
The set of integers, n: {. . . -4, -3, -2, 1, 0, 1, 2, 3, 4, 5, . . .}
• So n will give all positive and negative integers.
• We want the general form when π is multiplied by +ve and -ve integers.
• Obviously, that general form will be: nπ, where n is the set of integers.
10. So we can write:
sine will become zero when the angle is nπ, where n is any integer
Next we will see cos x. It can be written in 10 steps:
1. From the discussions in previous sections, we know that:
• cos x = 0 when the needle points towards B and D
♦ At B, the angle is ${\frac{\pi}{2}}^c$
♦ At D, the angle is ${\frac{3\pi}{2}}^c$
(Needle is rotating in the anticlockwise direction)
• So we get: $\cos \frac{\pi}{2}=0$ and $\cos \frac{3\pi}{2}=0$
2. After completing one revolution, if the needle reaches B again, the cosine will again become zero. In such a situation, the angle of rotation is ${2\pi+\frac{\pi}{2}=\frac{5\pi}{2}}^c$
♦ So we can write: $\cos \frac{5\pi}{2}=0$
• After completing one revolution, if the needle reaches D again, the cosine
will again become zero. In such a situation, the angle of rotation is
${2\pi+\frac{3\pi}{2}=\frac{7\pi}{2}}^c$
♦ So we can write: $\cos \frac{7\pi}{2}=0$
3. After completing two revolution, if the needle reaches B again, the cosine
will again become zero. In such a situation, the angle of rotation is
${4\pi+\frac{\pi}{2}=\frac{9\pi}{2}}^c$
♦ So we can write: $\cos \frac{9\pi}{2}=0$
• After completing two revolution, if the needle reaches D again, the cosine
will again become zero. In such a situation, the angle of rotation is
${4\pi+\frac{3\pi}{2}=\frac{11\pi}{2}}^c$
♦ So we can write: $\cos \frac{11\pi}{2}=0$
4. We can write like this up to infinity. The angles at which cosine becomes zero are:
${\frac{\pi}{2}}^c,\, {\frac{3\pi}{2}}^c,\, {\frac{5\pi}{2}}^c,\, {\frac{7\pi}{2}}^c,\, {\frac{9\pi}{2}}^c,\,.\,.\,.$
• We see a pattern: They are all odd multiples of $\frac{\pi}{2}$
♦ That is, $\frac{\pi}{2}$ is multiplied by the odd numbers 1, 3, 5, 7, . . .
5. Next let us see rotation in the clockwise direction. From the discussions in previous sections, we know that:
• cos x = 0 when the needle points towards D and B
♦ At D, the angle is $-{\frac{\pi}{2}}^c$
♦ At B, the angle is $-{\frac{3\pi}{2}}^c$
(Needle is rotating in the clockwise direction)
• So we get: $\cos \left(-\frac{\pi}{2}\right)=0$ and $\cos \left(-\frac{3\pi}{2}\right)=0$
6.
After completing one revolution, if the needle reaches D again, the
cosine will again become zero. In such a situation, the angle of rotation
is ${-2\pi-\frac{\pi}{2}=-\frac{5\pi}{2}}^c$
♦ So we can write: $\cos \left(-\frac{5\pi}{2}\right)=0$
• After completing one revolution, if the needle reaches B again, the cosine
will again become zero. In such a situation, the angle of rotation is
${-2\pi+\frac{3\pi}{2}=-\frac{7\pi}{2}}^c$
♦ So we can write: $\cos \left(-\frac{7\pi}{2}\right)=0$
7. After completing two revolution, if the needle reaches D again, the cosine
will again become zero. In such a situation, the angle of rotation is
${-4\pi-\frac{\pi}{2}=-\frac{9\pi}{2}}^c$
♦ So we can write: $\cos \left(-\frac{9\pi}{2}\right)=0$
• After completing two revolution, if the needle reaches B again, the cosine
will again become zero. In such a situation, the angle of rotation is
${-4\pi-\frac{3\pi}{2}=-\frac{11\pi}{2}}^c$
♦ So we can write: $\cos \left(-\frac{11\pi}{2}\right)=0$
8. We can write like this up to infinity. The angles at which cosine becomes zero are:
${-\frac{\pi}{2}}^c,\, {-\frac{3\pi}{2}}^c,\, {-\frac{5\pi}{2}}^c,\, {-\frac{7\pi}{2}}^c,\, {-\frac{9\pi}{2}}^c,\,.\,.\,.$
• We see a pattern: They are all negative odd multiples of $\frac{\pi}{2}$
♦ That is, $\frac{\pi}{2}$ is multiplied by the negative odd numbers -1, -3, -5, -7, . . .
9. Let us try to obtain a general form:
• In step (4), we got positive odd numbers 1, 3, 5, 7, . . .
• In step (8), we got negative odd numbers -1, -3, -5, -7, . . .
• In our previous classes, we have seen a general form which will give both positive and negative odd numbers:
(2n+1) where n is the set of integers: {. . . -4, -3, -2, 1, 0, 1, 2, 3, 4, 5, . . .}
• Let us see some examples:
♦ When n = -2, (2n+1) = -3
♦ When n = -1, (2n+1) = -1
♦ When n = 0, (2n+1) = 1
♦ When n = 2, (2n+1) = 5
♦ When n = 5, (2n+1) = 11
• So (2n+1) will give all positive and negative odd numbers when integers are put in place of n
• We want the general form when $\frac{\pi}{2}$ is multiplied by +ve and -ve odd numbers.
• Obviously, that general form will be:
$\frac{(2n+1)\pi}{2}$, where n is the set of integers.
10. So we can write:
cosine will become zero when the angle is $\frac{(2n+1)\pi}{2}$, where n is any integer.
Let us write a summary of all the steps that we wrote in this section. It can be written in steps:
1. Trigonometric ratios like sin x, cos x etc., can be written as trigonometric functions: f(x) = sin x, f(x) = cos x, f(x) = sec x etc.,
2. Any real number can be used as input x for those trigonometric functions.
♦ There are a few exceptions. Some real numbers are not allowed
♦ We will see them in the next section
3. f(x) = sin x will become zero if input x is nπ, where n is any integer.
4. f(x) = cos x will become zero if input x is $\frac{(2n+1)\pi}{2}$, where n is any integer.
In
the next
section, we will see graphs of various trigonometric functions.
Previous
Contents
Next
Copyright©2021 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment