In the previous section, we saw the trigonometric ratios of acute angles. We also saw a new method for finding trigonometric ratios. In this section, we will see trigonometric ratios of obtuse angles.
The details can be written in steps:
1. Recall the unit circle that we saw in the previous section.
• The ray indicated by the red arrow stopped rotation before reaching 90o.
♦ So x was an acute angle.
2. But for our present discussion, the ray has rotated beyond 90o. This is shown in fig.3.17 below:
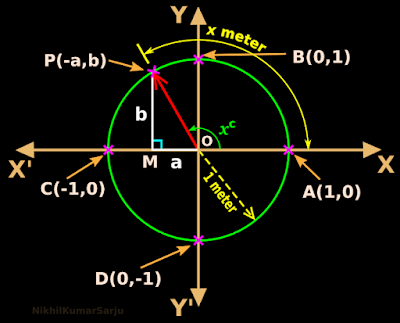 |
| Fig.3.17 |
• The angle of rotation x is now greater than 90o.
• The ray is now in the second quadrant.
3. In the traditional method, we use a right triangle to find sine and cosine.
• A right triangle will have a hypotenuse.
• So $\text{sine}=\frac{\text{opposite side}}{\text{hypotenuse}}~\text{and}~\text{cosine}=\frac{\text{adjacent side}}{\text{hypotenuse}}$.
4. But in our present case, the angle x is greater than 90o.
• No right triangle can be drawn with one of the angle greater than 90o. If there is no right triangle, there is no hypotenuse. So we cannot calculate sine and cosine using the traditional method.
• In such a situation, we use the new method that we saw at the end of the previous section.
5. Applying the new method to the angle x in fig.3.17 above, we get:
♦ sin x = y coordinate of P = b
♦ cos x = x coordinate of P = a
6. We can easily calculate a and b using the right triangle OMP.
Let us see an example. It can be written in 3 steps:
(i) Suppose that, x = ${\frac{5\pi}{6}}^c$ (150o).
Then ∠MOP = (180 - 150) = 30o
(ii) So we get:
$\begin{eqnarray}
a &=& OP \cos 30 = 1 \times \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2} \nonumber \\
b &=& OP \sin 30 = 1 \times \frac{1}{2}=\frac{1}{2} \nonumber \
\end{eqnarray}$
• Thus the coordinates of P are $\left(-\frac{\sqrt{3}}{2},\frac{1}{2} \right)$
(iii) So based on the new method, we get:
♦ sin 150 = y coordinate of P = $\frac{1}{2}$
♦ cos 150 = x coordinate of P = -$\frac{\sqrt{3}}{2}$
Another example:
(i) Suppose that, x = ${\frac{25\pi}{36}}^c$ (125o).
• Then ∠MOP = (180 - 125) = 55o
• 55o is an acute angle. It's sine and cosine can be obtained from standard tables or by using a calculator.
• We have: sin 55 = 0.8192 and cos 55 = 0.5736
(ii) So we get:
a = OP cos 55 = 1 × 0.5736 = 0.5736
b = OP sin 55 = 1 × 0.8192 = 0.8192
• Thus the coordinates of P are (-0.5736, 0.8192)
(iii) So based on the new method, we get:
♦ sin 125 = y coordinate of P = 0.8192
♦ cos 125 = x coordinate of P = -0.5736
• The following screen shot from a scientific calculator confirms the result of sine value. The reader may check the cosine value also.
7. From the two examples, we can see an interesting relation. It can be written in 3 steps:
(i) In example 1, we get:
♦ sin 150 = $\frac{1}{2}$ = sin 30
♦ cos 150 = -$\frac{\sqrt{3}}{2}$ = -cos 30
(ii) In example 2, we get:
♦ sin 125 = 0.8192 = sin 55
♦ cos 125 = -0.5736 = -cos 55
(iii) Angles between 90 and 180 can be related to 180. In our present examples, 150 = (180-30) and 125 = (180-55)
• We can write:
♦ sin (180-30) = -$\frac{1}{2}$ = sin 30
♦ cos (180-30) = -$\frac{\sqrt{3}}{2}$ = -cos 30
♦ sin (180-55) = -0.8192 = sin 55
♦ cos (180-55) = -0.5736 = -cos 55
• So we can write the general form:
♦ sin (180-x) = sin x
♦ cos (180-x) = -cos x
8. Next we will find sin180 and cos 180
It can be explained in 3 steps:
(i) Suppose that, the rotation of the ray stops at such a position that, x is very close to πc (180o).
• For example, the rotation may stop when the angle is 179.999999o
♦ Then P will be very close to C
(ii) In such a situation,
♦ b will be very small.
✰ It can be taken to be equal to zero
♦ a will be very close to OC
✰ It can be taken to be equal to OC
(iii) So we get coordinates (a,b) of P as: (-1, 0)
• An angle very close to 180o can be taken to be equal to 180o.
• Then we can write:
♦ cos 180 = x coordinate of P = a = -1
♦ sin 180 = y coordinate of P = b = 0
9. Next we will see the case when the rotation is greater than 180o. The following steps from (10) to (17) will give the details:
10. In fig.3.18 below, the ray has rotated beyond 180o.
 |
| Fig.3.18 |
11. In the traditional method, we use a right triangle to find sine and cosine.
• A right triangle will have a hypotenuse.
• So $\text{sine}=\frac{\text{opposite side}}{\text{hypotenuse}}~\text{and}~\text{cosine}=\frac{\text{adjacent side}}{\text{hypotenuse}}$.
12. But in our present case, the angle x is greater than 90o.
• No right triangle can be drawn with one of the angle greater than 90o. If there is no right triangle, there is no hypotenuse. So we cannot calculate sine and cosine using the traditional method.
• In such a situation, we use the new method that we saw at the end of the previous section.
13. Applying the new method to the angle x in fig.3.16 above, we get:
♦ sin x = y coordinate of P = b
♦ cos x = x coordinate of P = a
14. We can easily calculate a and b using the right triangle OMP.
Let us see an example. It can be written in 3 steps:
(i) Suppose that, x = ${\frac{7\pi}{6}}^c$ (210o).
Then ∠MOP = (210 - 180) = 30o
(ii) So we get:
$\begin{eqnarray}
a &=& OP \cos 30 = 1 \times \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2} \nonumber \\
b &=& OP \sin 30 = 1 \times \frac{1}{2}=\frac{1}{2} \nonumber \
\end{eqnarray}$
• Thus the coordinates of P are $\left(-\frac{\sqrt{3}}{2},-\frac{1}{2} \right)$
(iii) So based on the new method, we get:
sin 210 = y coordinate of P = -$\frac{1}{2}$
cos 210 = x coordinate of P = -$\frac{\sqrt{3}}{2}$
Another example:
(i) Suppose that, x = ${\frac{47\pi}{36}}^c$ (235o).
Then angleMOP = (235 - 180) = 55o
55o is an acute angle. it's sine and cosine can be obtained from standard tables or by using a calculator.
We have: sin 55 = 0.8192 and cos 55 = 0.5736
(ii) So we get:
a = OP cos 55 = 1 × 0.5736 = 0.5736
b = OP sin 55 = 1 × 0.8192 = 0.8192
• Thus the coordinates of P are (-0.5736, -0.8192)
(iii) So based on the new method, we get:
sin 235 = y coordinate of P = -0.8192
cos 235 = x coordinate of P = -0.5736
16. From the two examples, we can see an interesting relation. It can be written in 3 steps:
(i) In example 1, we get:
♦ sin 210 = -$\frac{1}{2}$ = -sin 30
♦ cos 210 = -$\frac{\sqrt{3}}{2}$ = -cos 30
(ii) In example 2, we get:
♦ sin 235 = -0.8192 = -sin 55
♦ cos 235 = -0.5736 = -cos 55
(iii) Angles between 180 and 270 can be related to 180. In our present examples, 210 = (180+30) and 235 = (180+55)
• We can write:
♦ sin (180+30) = -$\frac{1}{2}$ = -sin 30
♦ cos (180+30) = -$\frac{\sqrt{3}}{2}$ = -cos 30
♦ sin (180+55) = -0.8192 = -sin 55
♦ cos (180+55) = -0.5736 = -cos 55
• So we can write the general form:
♦ sin (180+x) = -sin x
♦ cos (180+x) = -cos x
17. Next we will find sin 270 and cos 270
It can be explained in steps:
(i) Suppose that, the rotation of the ray stops at such a position that, x is very close to ${\frac{3\pi}{2}}^c$ (270o).
• For example, the rotation may stop when the angle is 269.999999o
♦ Then P will be very close to D
(ii) In such a situation,
♦ a will be very small.
✰ It can be taken to be equal to zero
♦ b will be very close to OD
✰ It can be taken to be equal to OD
(iii) So we get coordinates (a,b) of P as: (0,-1)
• An angle very close to 270o can be taken to be equal to 270o.
• Then we can write:
♦ cos 270 = x coordinate of P = a = 0
♦ sin 270 = y coordinate of P = b = -1
18. Next we will see the case when the rotation is greater than 270o.
The following steps from (19) to (24) will give the details:
19. In fig.3.19 below, the ray has rotated beyond 270o.
 |
| Fig.3.19 |
20. As before, here also, we cannot use the traditional method because, the angle is greater than 90o. So we apply the new method using coordinates (a,b).
21. Applying the new method to the angle x in fig.3.19 above, we get:
♦ sin x = y coordinate of P = b
♦ cos x = x coordinate of P = a
22. We can easily calculate a and b using the right triangle OMP.
Let us see an example. It can be written in 3 steps:
(i) Suppose that, x = ${\frac{5\pi}{3}}^c$ (300o).
• Then ∠MOP = (300 - 270) = 30o
(ii) So we get:
$\begin{eqnarray}
a &=& OP \cos 30 = 1 \times \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2} \nonumber \\
b &=& OP \sin 30 = 1 \times \frac{1}{2}=\frac{1}{2} \nonumber \
\end{eqnarray}$
• Thus the coordinates of P are $\left(\frac{\sqrt{3}}{2},-\frac{1}{2} \right)$
(iii) So based on the new method, we get:
♦ sin 300 = y coordinate of P = $\frac{1}{2}$
♦ cos 300 = x coordinate of P = -$\frac{\sqrt{3}}{2}$
Another example:
(i) Suppose that, x = ${\frac{65\pi}{36}}^c$ (325o).
• Then ∠MOP = (325 - 270) = 55o
• 55o is an acute angle. it's sine and cosine can be obtained from standard tables or by using a calculator.
• We have: sin 55 = 0.8192 and cos 55 = 0.5736
(ii) So we get:
a = OP cos 55 = 1 × 0.5736 = 0.5736
b = OP sin 55 = 1 × 0.8192 = 0.8192
• Thus the coordinates of P are (0.5736, -0.8192)
(iii) So based on the new method, we get:
sin 235 = y coordinate of P = -0.8192
cos 235 = x coordinate of P = 0.5736
23. From the two examples, we can see an interesting relation. It can be written in 3 steps:
(i) In example 1, we get:
♦ sin 300 = -$\frac{1}{2}$ = -sin 30
♦ cos 300 = -$\frac{\sqrt{3}}{2}$ = -cos 30
(ii) In example 2, we get:
♦ sin 325 = -0.8192 = -sin 55
♦ cos 325 = 0.5736 = cos 55
(iii) Angles between 270 and 360 can be related to 270. In our present examples, 300 = (270+30) and 325 = (270+55)
• We can write:
♦ sin (270+30) = -$\frac{1}{2}$ = -sin 30
♦ cos (270+30) = $\frac{\sqrt{3}}{2}$ = cos 30
♦ sin (270+55) = -0.8192 = -sin 55
♦ cos (270+55) = 0.5736 = cos 55
• So we can write the general form:
♦ sin (270+x) = -sin x
♦ cos (270+x) = cos x
24. Next we will find sin 360 and cos 360
It can be explained in steps:
(i) Suppose that, the rotation of the ray stops at such a position that, x is very close to ${2\pi}}^c$ (360o).
• For example, the rotation may stop when the angle is 359.999999o
♦ Then P will be very close to A
(ii) In such a situation,
♦ b will be very small.
✰ It can be taken to be equal to zero
♦ a will be very close to OA
✰ It can be taken to be equal to OA
(iii) So we get coordinates (a,b) of P as: (1,0)
• An angle very close to 360o can be taken to be equal to 360o.
• Then we can write:
♦ cos 360 = x coordinate of P = a = 1
♦ sin 360 = y coordinate of P = b = 0
25. Next we will see the case when the rotation is greater than 360o.
The following steps from (26) to (32) will give the details:
26. In fig.3.20 below, the ray has rotated beyond 360o.
 |
| Fig.3.20 |
• The ray is now back in the first quadrant.
27. We see that, the ray is now in a position that we saw in the previous section.
• So we can use either the traditional method or the new method.
• Whatever be the method,
♦ The result will be same as that obtained for an acute angle.
• This can be explained in 3 steps:
(i) Suppose that, the ray starts from the x axis and rotates through an angle x1c where x1 is less than ${\frac{\pi}{2}}^c$
We can easily calculate a and b
(ii) Suppose that, the ray starts from the x axis, rotate through 2π (360o) and further rotate through the same x1 as in (i).
Here also, we can easily calculate a and b.
(iii) We can compare the results:
♦ The a and b calculated in (ii)
♦ will be exactly same as
♦ The a and b calculated in (i)
28. So we can write:
♦ sin x = sin (2π+x1) = sin x1
♦ cos x = cos (2π+x1) = cos x1
✰ Where x = (2π+x1) and x1 is an acute angle.
29. In the fig.3.20, the ray completed one revolution and then further rotated through x1. So the angle of rotation x = (2π+x1).
We wrote:
♦ sin x = sin (2π+x1) = sin x1
♦ cos x = cos (2π+x1) = cos x1
✰ Where x = (2π+x1) and x1 is an acute angle.
30. In some cases, the ray may complete two revolutions and then further rotate through x1. Then the angle of rotation x will be (2 × 2π+x1)
• We can write:
♦ sin x = sin (2 × 2π+x1) = sin x1
♦ cos x = cos (2 × 2π+x1) = cos x1
✰ Where x = (2 × 2π+x1) and x1 is an acute angle.
• We see that, the sine and cosine values do not change.
31. In some cases, the ray may complete three revolutions and then further
rotate through x1. Then the angle of rotation x will be (3 × 2π+x1)
• We can write:
♦ sin x = sin (3 × 2π+x1) = sin x1
♦ cos x = cos (3 × 2π+x1) = cos x1
✰ Where x = (3 × 2π+x1) and x1 is an acute angle.
• We see that, the sine and cosine values do not change.
32. In general, the ray may complete n revolutions and then further
rotate through x1. Then the angle of rotation x will be (n × 2π+x1)
• We can write:
♦ sin x = sin (2nπ+x1) = sin x1
♦ cos x = cos (2nπ+x1) = cos x1
✰ Where x = (2nπ+x1) and x1 is an acute angle.
• The sine and cosine values will not change.
• We have seen 32 steps in this section. Those steps are related to obtuse angles.
• We have seen 31 steps in the previous section. Those steps are related to acute angles.
• Based on all those steps, we can write four points:
1. When the ray rotates in the anticlockwise direction, we are able to find the sine and cosine of any given xc.
• All we need to do is, apply the following two steps:
(i) Find the base ‘a’ and altitude ‘b’ of the triangle OMP.
(ii) Using the base and altitude, write the coordinates of point P.
♦ The x coordinate will be the cosine of that angle.
♦ The y coordinate will be the sine of that angle.
2. We can write the signs also:
• When the ray is in the first quadrant,
♦ sine will be +ve
♦ cosine will be +ve
• When the ray is in the second quadrant,
♦ sine will be +ve
♦ cosine will be -ve
• When the ray is in the third quadrant,
♦ sine will be -ve
♦ cosine will be -ve
• When the ray is in the fourth quadrant,
♦ sine will be -ve
♦ cosine will be +ve
3. We can write the sine and cosine at the points A, B, C and D where the unit circle cuts the axes:
• The unit circle cuts the +ve side of the x axis at A.
♦ At A, x = 0c
♦ sin 0 = 0, cos 0 = 1
• The unit circle cuts the +ve side of the y axis at B.
♦ At B, x = ${\frac{\pi}{2}}^c$
♦ sin $\frac{\pi}{2}$ = 1, cos $\frac{\pi}{2}$ = 0
• The unit circle cuts the -ve side of the x axis at C.
♦ At C, x = πc
♦ sin π = 0, cos π = -1
• The unit circle cuts the -ve side of the y axis at D.
♦ At D, x = ${\frac{3\pi}{2}}^c$
♦ sin $\frac{3\pi}{2}$ = -1, cos $\frac{3\pi}{2}$ = 0
• The ray completes one revolution and returns to A
♦ Then at A, x = 2πc
♦ sin 2π = 0, cos 2π = 1
4. From step 7(iii) below fig.3.17 at the beginning of this section, we get two useful results:
♦ sin (180-x) = sin x
♦ cos (180-x) = -cos x
We have completed a discussion on trigonometric ratios when the ray rotates in the anticlockwise direction. In
the next
section, we will see clockwise rotation.
Previous
Contents
Next
Copyright©2021 Higher secondary mathematics.blogspot.com

No comments:
Post a Comment