In the previous section, we saw how the trigonometric ratios of any angle (acute or obtuse) can be written by applying the new method. But the angles that we saw were obtained by rotating the ray in the anticlockwise direction. When the rotation is in the anticlockwise direction, angles will be +ve. In this section, we will see rotation in the clockwise direction. When the rotation is in the clockwise direction, the angles will be negative.
In the previous section, we effectively used the new method for all positive angles. Once we are familiar with that process, we can write the trigonometric ratios of negative angles also. We will need to write only minimum steps.
1. In fig.3.21(a) below, the ray began it’s rotation from the x axis. The rotation is in the clockwise direction. So the angle is -xc.
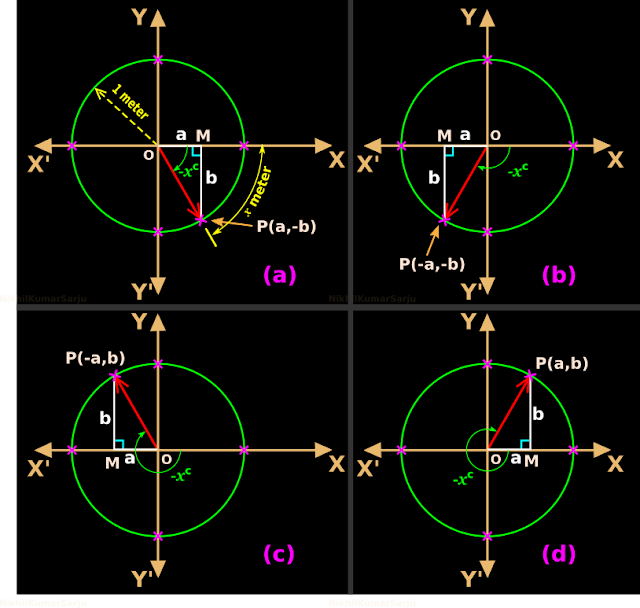 |
| Fig.3.21 |
• From the right triangle OMP, we get:
♦ $\cos |x| = \frac{OM}{OP} = \frac{OM}{1} = OM = a$
♦ $\sin |x| = \frac{PM}{OP} = \frac{PM}{1} = PM = b$
(Note that, we are taking the absolute value of angle x. This is because, all we want is to get the lengths a and b)
• Since P is in the fourth quadrant, the coordinates are (a, -b)
♦ sine value is the y coordinate -b
♦ cosine value is the x coordinate a
• So the new method works for negative angles also.
2. In fig.3.21(b) above, the ray began it’s rotation from the x axis.
The rotation is in the clockwise direction. So the angle is -xc.
• Here ∠MOP = (180 - |x|).
• From the right triangle OMP, we get:
♦ $\cos (180 - |x|) = \frac{OM}{OP} = \frac{OM}{1} = OM = a$
♦ $\sin (180 - |x|) = \frac{PM}{OP} = \frac{PM}{1} = PM = b$
• Since P is in the third quadrant, the coordinates are (-a, -b)
♦ sine value is the y coordinate -b
♦ cosine value is the x coordinate -a
• Let us see an example. It can be written in 3 steps:
(i) Suppose that, x = -125o
• Then ∠MOP = (180 - |-125|) = 55o
(ii) So we get:
♦ a = OM = cos 55 = 0.5736
♦ b = PM = sin 55 = 0.8192
• So the coordinates of P are: (-0.5736, -0.8192)
(iii) We can write:
♦ cos(-125) = -0.5736
♦ sin(-125) = -0.8192
• The following screenshot from a scientific calculator confirms the result for cosine value. The reader may check the sine value also.
• Here ∠MOP = (270 - |x|).
• From the right triangle OMP, we get:
♦ $\cos (270 - |x|) = \frac{OM}{OP} = \frac{OM}{1} = OM = a$
♦ $\sin (270 - |x|) = \frac{PM}{OP} = \frac{PM}{1} = PM = b$
• Since P is in the second quadrant, the coordinates are (-a, b)
♦ sine value is the y coordinate b
♦ cosine value is the x coordinate -a
4. In fig.3.21(d) above, the ray began it’s rotation from the x axis. The rotation is in the clockwise direction. So the angle is -xc.
• Here ∠MOP = (360 - |x|).
• From the right triangle OMP, we get:
♦ $\cos (360 - |x|) = \frac{OM}{OP} = \frac{OM}{1} = OM = a$
♦ $\sin (360 - |x|) = \frac{PM}{OP} = \frac{PM}{1} = PM = b$
• Since P is in the first quadrant, the coordinates are (a, b)
♦ sine value is the y coordinate b
♦ cosine value is the x coordinate a
We are now in a position to write the trigonometric ratios of negative angles also. Let us see some solved examples:
Solved example 3.23
Given that cos x = $-\frac{3}{5}$ and x lies in the third quadrant. Find the values of other five trigonometric ratios.
Solution:
1. Using the given information, we can draw two items:
(i) A ray in the third quadrant
(ii) Base 'a' of triangle OMP = $\frac{3}{5}$ meter
This is shown in fig.3.22(a) below:
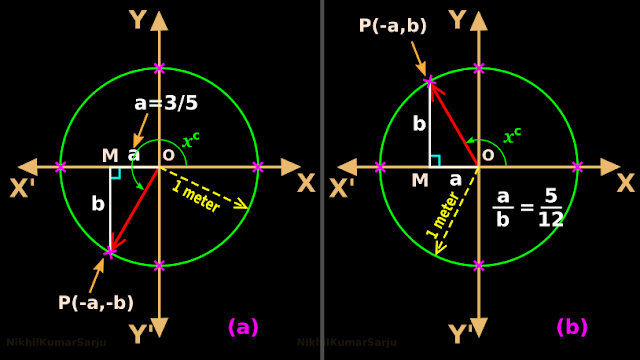 |
| Fig.3.22 |
• Note that:
♦ cosine is $-\frac{3}{5}$. But we are taking the length 'a' as $+\frac{3}{5}$.
♦ This is because, cosine value is a coordinate value.
♦ From the coordinate value, we obtain the length.
✰ A length cannot be negative.
2. Since it is a unit circle, OP = 1 meter
3. So we have two sides of the right triangle OMP.
• Then the third side PM = $\sqrt{1^2 - \left(\frac{3}{5} \right)^2} = \pm \frac{4}{5}$
4. Since length cannot be negative, we must take $+\frac{4}{5}$
• This third side PM is 'b'.
• Since P is in the third quadrant,
♦ x coordinate is negative
♦ y coordinate is negative
• So the coordinates (a,b) are: $\left(-\frac{3}{5},-\frac{4}{5} \right)$
5. Using the coordinates, we can write sin x and cos x:
sin x = y coordinate = $-\frac{4}{5}$
cos x = x coordinate = $-\frac{3}{5}$ (This is already given)
6. Using sin x and cos x, we can write tan x:
tan x = $\frac{\sin x}{\cos x}= \frac{-4/5}{-3/5}=\frac{4}{3}$
7. cot x = $\frac{1}{\tan x}= \frac{1}{4/3}=\frac{3}{4}$
8. csc x = $\frac{1}{\sin x}=\frac{1}{-4/5}=-\frac{5}{4}$
9. sec x = $\frac{1}{\cos x}=\frac{1}{-3/5}=-\frac{5}{3}$
Another method:
1. We have the identity: sin2x + cos2x = 1
⇒ sin2x = 1 - cos2x = $1 - \left(\frac{3}{5} \right)^2=\frac{16}{25}$
⇒ sin x = $\pm \frac{4}{5}$
2. Here we must carefully consider the sign. Because, it is not a length. It is the sine value. Sine value can be +ve or -ve.
• Given that, P is in the third quadrant. In the third quadrant, sine is -ve.
• So we get: sin x = $-\frac{4}{5}$
3. Once we have sin x and cos x, the remaining ratios can be calculated as in the first method. Steps (6) to (9).
Solved example 3.24
Given that cot x = $-\frac{5}{12}$ and x lies in the second quadrant. Find the values of other five trigonometric ratios.
Solution:
1. Using the given information, we can draw one item:
The ray in the second quadrant.
2. The coordinates of P will be (-a,b)
♦ b will be the altitude of the triangle OMP
♦ |-a| will be the base of the triangle OMP
3. Derivation of various trigonometric ratios:
♦ The sine of x can be obtained from 'b' by applying the appropriate sign.
♦ The cosine of x can be obtained from 'a' by applying the appropriate sign.
♦ The cotangent of x will be $\frac{a}{b}$ after applying the proper signs.
• So our task is to find 'a' and 'b'.
• We do not have to worry about finding appropriate signs because, the quadrant is known.
4. In triangle OMP, we can write: $\frac{a}{b}=\frac{5}{12}$.
So $a=\frac{5b}{12}$.
(Note that, given cotangent (-5/12) is related to the angle x. It is negative. But here, we are taking (a/b) ratio for the triangle OMP. Sides of a triangle cannot be negative)
5. In triangle OMP, we can also write: a2 + b2 = 1
• Substituting for 'a', we get: $\left(\frac{5b}{12} \right)^2+b^2=1$
• From this we get: b = $\pm \frac{12}{13}$
♦ Since 'b' is a length, we must take: b = $+\frac{12}{13}$
• Substituting for 'b' in (4), we get: $a=\frac{5}{12} \times \frac{12}{13} = \frac{5}{13}$.
6. Thus we get the coordinates of P:
♦ x coordinate of P =$-\frac{5}{13}$
♦ y coordinate of P =$\frac{12}{13}$
7. Now we can write sine and cosine of x
♦ sin x = y coordinate of P = $\frac{12}{13}$
♦ cos x = x coordinate of P = $-\frac{5}{13}$
8. Using sin x and cos x, we can write tan x:
tan x = $\frac{\sin x}{\cos x}= \frac{12/13}{-5/13}=-\frac{12}{5}$
9. cot x = $\frac{1}{\tan x}= \frac{1}{-12/5}=-\frac{5}{12}$ (This is already given)
10. csc x = $\frac{1}{\sin x}=\frac{1}{12/13}=-\frac{13}{12}$
11. sec x = $\frac{1}{\cos x}=\frac{1}{-5/13}=-\frac{13}{5}$
Another method:
1. We have the identity: 1 + cot2x = csc2x
⇒ csc2x = $1 + \left(-\frac{5}{12} \right)^2=\frac{169}{144}$
⇒ csc x = $\pm \frac{13}{12}$
2. Here we must carefully consider the sign. Because, it is not a length. It is the csc value. csc value can be +ve or -ve.
• Given that, P is in the second quadrant. In the second quadrant, sine is +ve. So csc must also be positive.
• So we get: csc x = $+\frac{13}{12}$
3. Now we can find sine value by taking the reciprocal of the csc value. We get:
sin x = $+\frac{12}{13}$
4. Next we can find cos x using sin x and the given cot x.
• We have: cot x = $-\frac{5}{12} = \frac{\cos x}{\sin x}=\frac{\cos x}{12/13}$
• Thus we get: cos x = $-\frac{5}{12} \times \frac{12}{13}=-\frac{5}{13}$
3. Once we have sin x and cos x, the remaining ratios can be calculated as in the first method. Steps (8) to (11).
Solved example 3.25
Find the value of $\sin \frac{31\pi}{3}$
Solution:
1. First we compare $\sin \frac{31\pi}{3} ~\text{with}~ 2\pi$
• For that, we convert 2𝞹 to a fraction form with denominator '3'.
♦ We get: $2\pi = \frac{6\pi}{3}$
• So obviously, $\sin \frac{31\pi}{3}$ is larger than 2𝞹.
2. That means, the ray has completed more than one revolutions.
• We need to find how many revolutions were completed.
• For that we do the division: $\frac{\frac{31\pi}{3}}{2 \pi}=\frac{31}{6}=5\frac{1}{6}$
• That means, the ray first completed 5 revolutions. Then it rotated by 1/6 of a revolution
3. 1/6 of a revolution is: $\frac{1}{6} \times 2 \pi= {\frac{\pi}{3}}^c$
• So we can write:
After completing 5 revolutions, the ray rotated through ${\frac{\pi}{3}}^c$
4. ${\frac{\pi}{3}}^c$ is 60o.
• Since the given angle is +ve, the rotations were done in the anticlockwise direction.
• After completing 5 revolutions in the anticlockwise direction, the ray further rotated by 60o. So P is in the first quadrant. This is shown in fig.3.23(a) below:
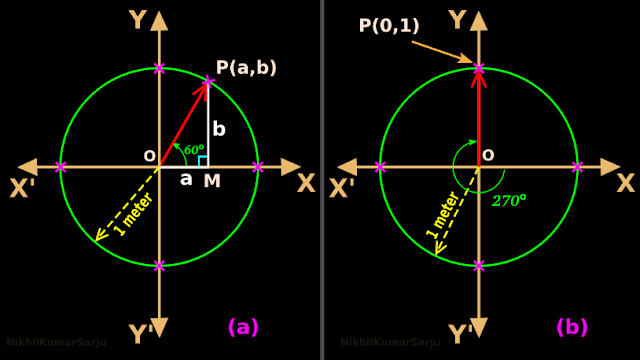 |
| Fig.2.23 |
• We want the y coordinate of P (because, y coordinate is the sine).
5. We already know the x coordinate in the following situation:
♦ when the ray is in the first quadrant.
♦ Also the ray makes 60o with the x axis.
• The x coordinate is $\frac{\sqrt{3}}{2}$ (see fig.3.14 of section 3.4)
6. So when the ray rotates through ${\frac{\pi}{3}}^c$ in the anticlockwise direction, the final position of P will have an x coordinate of $\frac{\sqrt{3}}{2}$
• That means: $\sin \frac{31\pi}{3}=\frac{\sqrt{3}}{2}$
Solved example 3.26
Find the value of cos (-1710o)
Solution:
1. First we compare the numerical value of -1710o with 360o
• Obviously, 1710 is larger than 360.
2. That means, the ray has completed more than one revolutions.
• We need to find how many revolutions were completed.
• For that we do the division: $\frac{1710}{360}=\frac{19}{4}=4\frac{3}{4}$
• That means, the ray first completed 4 revolutions. Then it rotated by 3/4 of a revolution.
3. 3/4 of a revolution is: $\frac{3}{4} \times 360= 270^o$
• So we can write:
After completing 4 revolutions, the ray rotated through 270o
4. Since the given angle is -ve, the rotations were done in the clockwise direction.
• After completing 4 revolutions in the clockwise direction, the ray further rotated by 270o. So P is in the +ve side of the y axis. This is shown in fig.3.23(b) above.
• We want the x coordinate of P (because, x coordinate is the cosine)
5. The x coordinate of P can be written without any difficulty because, P is exactly on the y axis. We see that, the x coordinate of P is zero.
6.
So when the ray rotates through -1710o, the final
position of P will have an x coordinate of zero.
• That means: cos (-1710o) = 0
Link to a few more examples are given below:
In
the next
section, we will see some basic details about trigonometric functions.
Previous
Contents
Next
Copyright©2021 Higher secondary mathematics.blogspot.com

No comments:
Post a Comment