In the previous section, we saw the details about Argand plane. In this section, we will see Polar representation.
Some basics can be written in 9 steps:
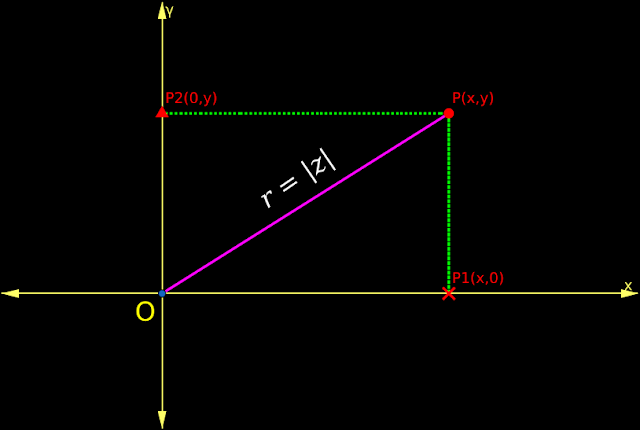
1. In fig.5.4 below, P(x,y) represents the complex number z = x+yi
 |
| Fig.5.4 |
• We have seen that, OP will be the modulus of z.
• Let the length of OP be r. Then we can write: OP = r = |z|
• PP1 is the perpendicular dropped from P onto the x axis.
• PP2 is the perpendicular dropped from P onto the y axis.
2. Let OP make an angle of 𝜽 radians with the positive side of the x axis.
• Then we get:
♦ OP1 = r cos 𝜽
♦ PP1 = r sin 𝜽
3. Now we can write the complex number in terms of r and 𝜽:
♦ OP1 = x. So we get x = r cos 𝜽
♦ PP1 = OP2 = y. So we get: y = r sin 𝜽
• Then the complex number z = x+yi can be written as: r cos 𝜽 + r i sin 𝜽
♦ This is same as: z = r(cos 𝜽 + i sin 𝜽)
4. So we have two methods to represent a complex number:
(i) z = x+yi
(ii) z = r(cos 𝜽 + i sin 𝜽)
• In the first method, two distances (x and y) will give the complex number.
♦ That is., the ordered pair (x,y) will give the complex number.
• In the second method, a distance (r) and an angle (𝜽) will give the complex number.
♦ That is., the ordered pair (r,𝜽) will give the complex number.
[Since 𝜽 is measured in radians, it will be a real number. So (r,𝜽) is an ordered pair of real numbers.]
• We have already seen that, r (which is the modulus) can be calculated using x and y as: $|z|=\sqrt{x^2+y^2}$
5. Writing a complex number in the form r(cos 𝜽 + i sin 𝜽) is called polar representation of a complex number.
• (r,𝜽) is called polar coordinates of the complex number.
• The origin is considered as the pole.
• 𝜽 should be measured from the +ve direction of the x axis.
♦ 𝜽 is called the argument of the complex number z.
♦ 𝜽 is also called the amplitude of the complex number z.
6. In the above five steps, the complex number that we considered was in the first quadrant.
•
But we may have to deal with complex numbers which are in the second,
third or fourth quadrants also. This is shown in fig.5.5 below:
 |
| Fig.5.5 |
• So 𝜽 can be any value between 0 and 2π.
• 𝜽 can be zero also. (This happens when the complex number is on the positive side of the x axis)
7. In chapter 3, we have seen that, even if 𝜽 is greater than $\frac{\pi}{2}$,
♦ cosine will give the x coordinate of P
♦ sine will give the y coordinate of P
♦ (Details here)
• So
even if 𝜽 (argument) of a complex number is greater than
$\frac{\pi}{2}$, we can use the polar representation for that complex
number.
8. In chapter 3, we also saw that, 𝜽 can be greater than
2π. But then the results will be same as completing one or more full
rotations.
• So we will need only those values 'which are between 0 and 2π'. It will take care of all the four quadrants.
9. However, while dealing with complex numbers, mathematicians prefer another method. It can be written in 3 steps:
(i) If P is in the first or second quadrants, the argument is considered to be +ve.
• That is.,
♦ the rotation starts from the +ve side of the x axis in the anti-clockwise direction.
♦ the rotation ends at the -ve side of the x axis.
(ii) If P is in the third or fourth quadrants, the argument is considered to be -ve.
• That is.,
♦ the rotation starts from the +ve side of the x axis in the clockwise direction.
♦ the rotation ends at the -ve side of the x axis.
(iii) This method will also take care of all the four quadrants. It is shown in fig.5.6 below:
 |
| Fig.5.6 |
Now we will see some solved examples
Solved example 5.6
Represent the complex number $z=1+\sqrt{3}\,i$ in the polar form.
Solution:
1.
The complex number is given to us in the form x+yi. We have to convert
it into the form:
r[cos 𝜽 + i sin 𝜽]
• For that, we have to
find the polar coordinates (r,𝜽)
2. Since the two forms are equal, we can equate the corresponding parts:
♦ Equating the real parts, we get: x = r cos 𝜽
♦ Equating the imaginary parts, we get: y = r sin 𝜽
3. We know that $r=|z|=\sqrt{x^2+y^2}$
• So in our present case, we get:
$r=\sqrt{1^2+(\sqrt{3})^2}=\sqrt{1+3}=\sqrt{4}=\pm 2$
• r is the distance between the complex number and the origin. A distance cannot be -ve. So we can write: r = 2
4. From the results in (2), we get:
(i) $x=1=2 \cos \theta$
(ii) $y=\sqrt{3}=2 \sin \theta$
• We must find that value of 𝜽 which satisfies both (i) and (ii)
5. Taking ratios, (ii) to (i), we get:
$\frac{2 \sin \theta}{2 \cos \theta}=\frac{\sqrt{3}}{1}$
$\Rightarrow \tan \theta = \sqrt{3}$
• This is a trigonometrical equation. We learned to solve them in chapter 3. (Details here)
6. We know that, $\tan \frac{\pi}{3}=\sqrt{3}$
• So we can write: $\tan \frac{\pi}{3}=\tan \theta = \sqrt{3}$
• From this we get: $\theta = \frac{\pi}{3}$
Check:
• Substituting this value of 𝜽 in 4(i), we get:
$1=2 \cos \frac{\pi}{3} = 2 × \frac{1}{2} = 1$. This is true.
• Substituting this value of 𝜽 in 4(ii), we get:
$\sqrt{3}=2 \sin \frac{\pi}{3} = 2 × \frac{\sqrt{3}}{2} = \sqrt{3}$. This is true.
• So $\theta = \frac{\pi}{3}$ is acceptable.
7. There is another possible value for 𝜽. It can be calculated using the identity: tan 𝜽 = tan (π+𝜽)
• So we can write:
$\tan \frac{\pi}{3}=\tan \theta = \tan \left(\pi + \theta \right)= \tan \left(\pi + \frac{\pi}{3}\right) = \sqrt{3}$
• From this we get: $\tan \theta = \tan \left( \frac{4\pi}{3}\right) = \sqrt{3}$
• So $\theta = \frac{4\pi}{3}$
Check:
• Substituting this value of 𝜽 in 4(i), we get:
$1=2 \cos \frac{4\pi}{3} = 2 × -\frac{1}{2} = -1$. This is not true.
• Substituting this value of 𝜽 in 4(ii), we get:
$\sqrt{3}=2 \sin \frac{4\pi}{3} = 2 × - \frac{\sqrt{3}}{2} = -\sqrt{3}$. This is not true.
• Value of 𝜽 will be acceptable only if both equations 4(i) and 4(ii) are satisfied. So $\theta = \frac{4\pi}{3}$ is not acceptable.
8. Thus we get the values of r and 𝜽:
♦ From (3), we get: r = 2
♦ From (6),we get: $\theta = \frac{4\pi}{3}$
9. So the required polar form is: $z=2\left(\sin \frac{\pi}{3}+i \cos \frac{\pi}{3} \right)$.
• The point P in fig.5.7(a) below represents the given complex number in the Argand plane.
 |
| Fig.5.7 |
In the above example, we had to perform two checks.
Those two checks can be avoided by using a simple trick. This can be
explained in 4 steps:
1. We saw that two values of 𝜽 are possible. This is because, tangent of 𝜽 can be $\sqrt{3}$ on two occasions:
(i) When 𝜽 = $\frac{\pi}{3}$
(ii) When 𝜽 = $\frac{4\pi}{3}$
2. But only one value is acceptable because in total, three equations should be satisfied:
(i) $1=2 \cos \theta$
(ii) $\sqrt{3}=2 \sin \theta$
(iii) $\sqrt{3}=\tan \theta$
3. We see that both sin 𝜽 and cos 𝜽 are +ve.
• This is possible only when 𝜽 is in the first quadrant.
4. So we must choose that 𝜽 which is in the first quadrant.
• Using this trick, the two checks can be avoided.
Solved example 5.7
Convert the complex number $z=\frac{-16}{1+\sqrt{3}\,i}$ in the polar form.
Solution:
1.
First we have to convert the given complex number into the form x+yi. It can be done as shown below:
$\begin{array}{ll}
\frac{-16}{1+\sqrt{3}\,i}&{}={}&\frac{-16}{1+\sqrt{3}\,i} × \frac{1-\sqrt{3}\,i}{1-\sqrt{3}\,i}& {} &{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& \frac{(-16)(1-\sqrt{3}\,i)}{1^2-(\sqrt{3})^2(i)^2}&{} \\
\phantom{\frac{1}{2-3i}}&{}&\color
{green}{(a+b)(a-b)=a^2-b^2} &{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& \frac{(-16)(1-\sqrt{3}\,i)}{1-(3)(-1)}&{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& \frac{(-16)(1-\sqrt{3}\,i)}{4}&{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& -4(1-\sqrt{3}\,i)&{} \\
\phantom{\frac{-16}{1+\sqrt{3}\,i}}&{}={}& -4+4\sqrt{3}\,i&{} \\
\end{array}$
2. Now the complex number is in the form x+yi. We have to convert
this into the form:
r[cos 𝜽 + i sin 𝜽]
• For that, we have to
find the polar coordinates (r,𝜽)
3. Since the two forms are equal, we can equate the corresponding parts:
♦ Equating the real parts, we get: x = r cos 𝜽
♦ Equating the imaginary parts, we get: y = r sin 𝜽
4. We know that $r=|z|=\sqrt{x^2+y^2}$
• So in our present case, we get:
$r=\sqrt{(-4)^2+(4\sqrt{3})^2}=\sqrt{16+(16 × 3)}=\sqrt{64}=\pm 8$
• r is the distance between the complex number and the origin. A distance cannot be -ve. So we can write: r = 8
5. From the results in (3), we get:
(i) $x=-4=8 \cos \theta$
(ii) $y=4\sqrt{3}=8 \sin \theta$
• cos 𝜽 is -ve and sin 𝜽 is +ve. So 𝜽 is in the second quadrant.
6. Taking ratios, (ii) to (i), we get:
$\frac{8 \sin \theta}{8 \cos \theta}=\frac{4\sqrt{3}}{-4}$
$\Rightarrow \tan \theta = -\sqrt{3}$
• This is a trigonometrical equation. We learned to solve them in chapter 3. (Details here)
7. We know that, $\tan \frac{\pi}{3}=\sqrt{3}$
• We have the identity: tan (π-𝜽) = -tan 𝜽
If we put $\theta = \frac{\pi}{3}$, we get:
$\tan \left(\pi - \frac{\pi}{3} \right)=-\tan \frac{\pi}{3} = -\sqrt{3}$
$\Rightarrow \tan \left(\frac{2\pi}{3} \right)=-tan \frac{\pi}{3} = -\sqrt{3}$
$\Rightarrow \tan \theta = \tan \left(\frac{2\pi}{3} \right) = -\sqrt{3}$
• From this we get: $\theta = \frac{2\pi}{3}$
8. There is another possible value for 𝜽. It can be calculated using the identity: tan 𝜽 = tan (π+𝜽)
• So we can write:
$\tan \frac{2\pi}{3}=\tan \theta = \tan \left(\pi + \theta \right)= \tan \left(\pi + \frac{2\pi}{3}\right) = -\sqrt{3}$
• From this we get: $\tan \theta = \tan \left( \frac{5\pi}{3}\right) = -\sqrt{3}$
• So $\theta = \frac{5\pi}{3}$
9. So we have two values:
• From (7), we have: $\theta = \frac{2\pi}{3}$
♦ This is in the second quadrant.
• From (8), we have: $\theta = \frac{5\pi}{3}$
♦ This is in the fourth quadrant.
10. In step (5), we saw that 𝜽 is in the second quadrant.
• So $\theta = \frac{2\pi}{3}$ is the acceptable value.
11. Thus we get the values of r and 𝜽:
♦ From (4), we get: r = 8
♦ From (10),we get: $\theta = \frac{2\pi}{3}$
12. So the required polar form is: $z=8\left(\sin \frac{2\pi}{3}+i \cos \frac{2\pi}{3} \right)$.
• The point P in fig.5.7(b) above represents the given complex number in the Argand plane.
The link below gives a PDF file with more solved examples:
• In the next section, we will see quadratic equations.
Copyright©2022 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment