In the previous section, we completed a discussion on cosine formula. In this section we will see Napiers' Analogies.
• The list of trigonometric identities can be seen here.
◼ In any triangle, the following three relations are applicable:
$\begin{eqnarray}
&\text{(i)}\;\tan \frac{B-C}{2}&=\frac{b-c}{b+c}\, \cot \frac{A}{2} \\
&\text{(ii)}\;\tan \frac{C-A}{2}&=\frac{c-a}{c+a}\, \cot \frac{B}{2} \\
&\text{(iii)}\;\tan \frac{A-B}{2}&=\frac{a-b}{a+b}\, \cot \frac{C}{2} \
\end{eqnarray}$
Proof for (i) can be written in 3 steps:
1. Consider the three ratios in the sin formula.
• Each of those three ratios will give the same value for a triangle under consideration.
• So we can say that, any triangle will have it's own unique constant value 'k' which will be equal to each of the ratio in the sine formula.
• We can write: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=k$
• From this we get: a = k sin A, b = k sin B, c = k sin C
2. Consider the first analogy. $\frac{b-c}{b+c}$ can be modified as:
$\begin{eqnarray}
&\frac{b-c}{b+c}& =\frac{k \sin B-k \sin C}{k \sin B+k \sin C} \\
&{}& =\frac{k (\sin B- \sin C)}{k(\sin B+ \sin C)}\;=\frac{\sin B- \sin C}{\sin B+ \sin C} \\
&{}& =\frac{2\cos \frac{B+C}{2} \sin \frac{B-C}{2}}{2\sin \frac{B+C}{2} \cos \frac{B-C}{2}} \\
&{}& \text{(Using identity 20.d)} \\
&{}& =\cot \frac{B+C}{2} \tan \frac{B-C}{2} \\
&{}& =\cot \left(\frac{\pi}{2}-\frac{A}{2} \right) \tan \left(\frac{B-C}{2} \right) \\
&{}& \left[ \because \frac{\pi}{2}=\frac{A}{2}+\frac{B}{2}+\frac{C}{2}\right] \\
&{}& =\tan \left(\frac{A}{2} \right) \tan \left(\frac{B-C}{2} \right) \\
&{}& \left[ \because \text{using identities 5 and 6, }\cot \left(\frac{\pi}{2}-\frac{A}{2} \right)=\tan \left(\frac{A}{2} \right)\right] \\
&{}& =\frac{\tan \frac{B-C}{2} }{\cot \frac{A}{2}} \
\end{eqnarray}$
3. Thus we get: $\tan \frac{B-C}{2}=\frac{b-c}{b+c}\, \cot \frac{A}{2}$
• In the same way, we can prove (ii) and (iii) also.
Let us see the application of the above analogies. It can be written in steps:
1. Suppose that, we are given two sides b and c, and the included angle A
• Then we can easily calculate the RHS of (i)
2. That means, we can easily obtain $\tan \frac{B-C}{2}$
• From that, we can obtain $\frac{B-C}{2}$
• From that, we can obtain (B-C)
3. We are already given A.
• Using that A, we can find (B+C)
♦ Because, (B+C) = 180 - A
4. Thus we have two equations:
♦ One involving B+C
♦ The other involving B-C
• Using those equations, we can calculate B and C
Let us see some solved examples:
Solved example 3.97
In any triangle ABC, prove that
$a \sin(B-C)+b \sin(C-A)+c \sin(A-B)=0$
Solution:
1. We have: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=k$
• From this we get: a = k sin A, b = k sin B, c = k sin C
2. So we can modify the LHS of the given equation as:
k sin A sin(B-C) + k sin B sin(C-A) + k sin C sin(A-B)
3. Now we apply identity 8 to each of the three terms. We get:
k sin A [sin B cos C - cos B sin C] + k sin B [sin C cos A - cos c sin A] + k sin C [sin A cos B - cos A sin B]
4. Expanding this, we get:
k sin A sin B cos C - k sin A cos B sin C + k sin B sin C cos A - k sin B cos C sin A + k sin C sin A cos B - k sin C cos A sin B
• This is same as:
k [sin A sin B cos C - sin A cos B sin C + sin B sin C cos A - sin B
cos C sin A + sin C sin A cos B - sin C cos A sin B]
5. There are identical terms in the above expansion. The first set is underlined below:
k [sin A sin B cos C - sin A cos B sin C + sin B sin C cos A - sin B
cos C sin A + sin C sin A cos B - sin C cos A sin B]
• Being opposite in signs, they will cancel each other.
• The second set is under lined below:
k [- sin A cos B sin C + sin B sin C cos A + sin C sin A cos B - sin C cos A sin B]
• Being opposite in signs, they will cancel each other.
• The remaining set is:
k [+ sin B sin C cos A - sin C cos A sin B]
• Clearly, they will also cancel each other
6. In effect, the LHS becomes: k[0] = 0
• Thus we get LHS = RHS
Solved example 3.98
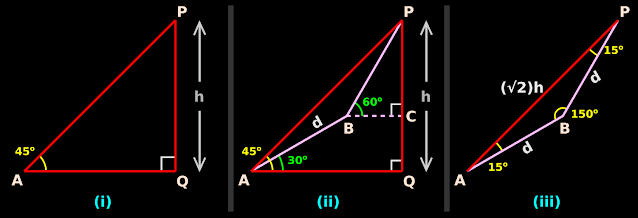
The angle of elevation of the top point P of the vertical tower PQ of height h from a point A is 45o and from a point B, the angle of elevation is 60o, where B is a point at a distance of d from the point A measured along the line AB which makes an angle 30o with AQ. Prove that d = h(√3-1)
Solution:
1. First, the instrument (used for measuring angles) is placed at A.
• When measured from A, the angle is 45o. This is shown in fig.3.45(i) below:
 |
| Fig.3.45 |
2. Then the instrument is taken to a point B.
• The distance of B from A is d. Also, AB makes an angle of 30o with PQ.
• When measured from B, the angle is 60o.
• These details must be added to the first fig. The modified fig. is fig.3.45(ii) above.
3. Let us calculate some important angles and sides:
(i) In ◺APQ, we have: ∠APQ = (180 - 90 - 45) = 45o
So it is an isosceles right triangle. We get: AQ = PQ = h
(ii) Since APQ is a right triangle, we get: $AP=\sqrt{AQ^2+PQ^2}=\sqrt{h^2+h^2}=\sqrt{2h^2}=\sqrt{2}\,h$
(iii) Inside ◺APQ, we have: ∠PAB = (45 - 30) = 15o
(iv) In ◺ PBC, we have: ∠BPC = (180 - 90 - 60) = 30o
(v) Inside ◺APQ, ∠APB = (45 - 30) = 15o
(vi) From (ii) and (iv), it is clear that ⃤⃤ APB is an isosceles triangle.
We have: AB = PB = d
(vii) Also in ⃤⃤ APB, we get: ABP = (180 - 15 -15) = 150o
4. So from 3(ii), (iii), (v), (vi) and (vii), we have all the angles and sides of ⃤⃤ APB.
This is shown in fig.3.45(iii).
• Now we can apply sine rule. We get:
$\frac{AP}{\sin B}=\frac{BP}{\sin A} \Rightarrow \frac{\sqrt{2}\,h}{\sin 150}=\frac{d}{\sin 15} \Rightarrow d=\frac{\sqrt{2}\,h \times \sin 15}{\sin 150}$
5. We need sin 15 and sin 150:
• We know that: sin 150 = sin (180 - 150) = sin 30 = $\frac{1}{2}$
• We have calculated sin 15 in an earlier section. (Solved example 3.30 in section 3.13)
♦ We got: $\sin 15 = \frac{\sqrt{3} - 1}{2 \sqrt 2}$
6. So the result in (4) becomes:
$\begin{eqnarray}
&{}& d=\frac{\sqrt{2}\,h \times \sin
15}{\sin 150} \\
&\Rightarrow& d=\frac{\sqrt{2}\,h \times \frac{\sqrt{3} - 1}{2 \sqrt 2}}{\frac{1}{2}} \\
&\Rightarrow& d=\frac{h \times \frac{\sqrt{3} - 1}{2}}{\frac{1}{2}} \\
&\Rightarrow& d=h(\sqrt{3} - 1) \
\end{eqnarray}$
Solved example 3.99
A lamp post is situated at the middle point M of the side AC of a triangular plot ABC with BC = 7 m, CA = 8 m and AB = 9 m. Lamp post subtends an angle 15o at the point B. Determine the height of the lamp post.
Solution:
1. In fig.3.46(i), the triangular plot ABC is lying on the ground. The plot is shown in red color.
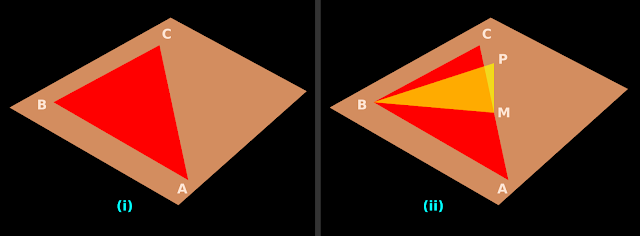 |
| Fig.3.46 |
• PM is the post. This is shown in fig.(ii). Given that: ∠PBM = 15o
• We are asked to find the height PM.
3. First we need to find ∠BAM
• This can be easily calculated by solving ⃤⃤ ABC. Since only the sides of ⃤⃤ ABC are given, we need to apply cosine rule. We get:
BC2` = AB2` + AC2` - 2 AB.AC cos (∠BAC)
• Substituting the known values, we get:
72` = 92` + 82` - 2 × 9 × 8 × cos (∠BAC)
• Thus we get: cos (∠BAC) = cos A = 0.6667
♦ Then A = 48.19o
• Consider the identity: cos x = cos (360-x)
♦ We get: cos 48.19 = cos (360-48.19) = cos 311.81 = 0.6667
♦ That means, A can be 48.19 or 311.81
♦ 311.81 is not acceptable because, it is greater than 180
• Thus we get: A = 48.19o
4. Now consider ⃤⃤ BAM.
• In this triangle, we have the measurements of two sides AB and AM, and the included angle A.
• So we can apply the cosine rule and find BM.
• We get: BM2` = AB2` + AM2` - 2 AB × AM × cos A
• Substituting the known values, we get:
BM2` = 92` + 42` - 2 × 9 × 8 × cos 48.19
• Thus we get: BM = 7 m
5. Finally, consider ⃤⃤ PBM
• We have: tan (∠PBM) = $\frac{PM}{BM}=\frac{PM}{BM}$
• Given that: ∠PBM = 15o
• Thus we get: tan 15 = $\frac{PM}{7}$
6. We have calculated tan 15 earlier as: $\frac{\sqrt{3}-1}{\sqrt{3}+1}$
• We can write: $\frac{\sqrt{3}-1}{\sqrt{3}+1}=\frac{PM}{7}$
• Thus we get: PM = $\frac{7(\sqrt{3}-1)}{\sqrt{3}+1}$
⇒ PM = $\frac{7(\sqrt{3}-1)}{\sqrt{3}+1}\times \frac{\sqrt{3}-1}{\sqrt{3}-1}$
⇒ PM = $\frac{7(\sqrt{3}-1)^2}{2}$
⇒ PM = $\frac{7(3+1-2 \sqrt{3})}{2}=\frac{7(4-2 \sqrt{3})}{2}$
⇒ PM = $\frac{7\times 2(2- \sqrt{3})}{2}=7(2- \sqrt{3})$ m
Link to some more solved examples is given below:
We have completed the discussion in this chapter. In
the next
chapter, we will see mathematical induction.
Previous
Contents
Next
Copyright©2021 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment