Chapter 5.4 - The Argand Plane

In the previous section, we saw modulus and conjugate of complex numbers. In this section, we will see Argand plane.

Some basics about Argand plane can be written in 7 steps:
1. We are familiar with Cartesian plane and ordered pairs.
• The Cartesian plane is formed by two perpendicular axes.
    ♦ The horizontal x axis.
    ♦ The vertical y axis.
• Ordered pairs like (2,3), (5, -1) etc., occupy unique positions in the Cartesian plane.
2. In our present case, we have complex numbers.
• The complex numbers have a real part and an imaginary part. These two parts can be written as an ordered pair.
• For example,
    ♦ The ordered pair related to 5+7i will be (5,7)
    ♦ The ordered pair related to 2-3i will be (2,-3)  
    ♦ The ordered pair related to -8-3i will be (-8,-3)
• The x coordinate of the ordered pair is the real part.
• The y coordinate of the ordered pair is the imaginary part.
• Since they are written as ordered pairs, we can mark them on a plane.
3. We cannot use Cartesian plane because, in a Cartesian plane, both x and y coordinates are real numbers.
    ♦ All numbers on the x axis are real numbers.
    ♦ All numbers on the y axis are real numbers.
4. So we develop a new plane called Argand plane.
• Like the Cartesian plane, the Argand plane is also formed by two perpendicular axes.
    ♦ The horizontal x axis is known as the real axis.
    ♦ The vertical y axis is known as the imaginary axis.
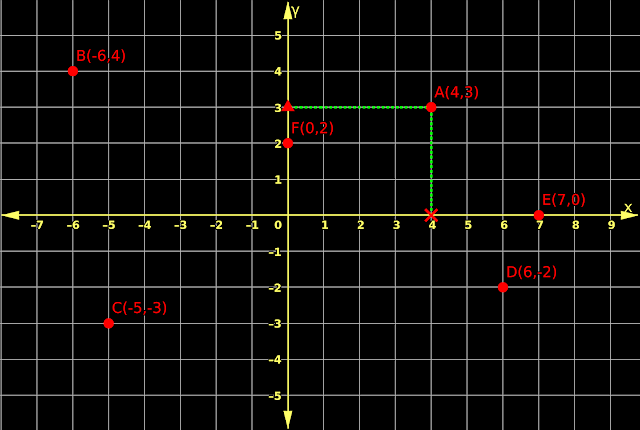
5. Let us see how a complex number say 4+3i is marked on the Argand plane. It can be written in 5 steps:
(i) We know that, in the complex number 4+3i, the real part is  ‘4’.
    ♦ So we mark 4 at the correct position on the real axis.
    ♦ This is indicated by the ❌ mark in fig.5.1 below:

Fig.5.1

(ii) We know that, in the complex number 4+3i, the imaginary part is  ‘3’.
    ♦ So we mark 3 at the correct position on the imaginary axis.
    ♦ This is indicated by the ⛰ mark.
(iii) Next we draw green dashed lines:
    ♦ Vertical green dashed line through 4
    ♦ Horizontal green dashed line through 3
(iv) The point of intersection of the two green dashed lines represents the complex number 4+3i
    ♦ This is indicated by the ● mark. It is labelled as A(4,3)
◼ The above process is already familiar to us. We have used it several times while working on Cartesian planes. If we use a graph paper, we will not need to draw horizontal and vertical green dashed lines.
(v) The point A(4,3) represents the complex number 4+3i
6. Five more complex numbers are marked in the fig.5.1
    ♦ B(-6,4) represents the complex number -6+4i
    ♦ C(-5,-3) represents the complex number -5-3i
    ♦ D(6,-2) represents the complex number 6-2i
    ♦ E(7,0) represents the complex number 7+0i
        ✰ Any complex number on the real axis will not have the imaginary part.
    ♦ F(0,2) represents the complex number 0+2i
        ✰ Any complex number on the imaginary axis will not have the real part.
7. We can write:
All points on the Argand plane will represent complex numbers.
• We can write the converse also:
If all points on a plane represent complex numbers, then that plane is called an Argand plane.
• The Argand plane is also known as Complex plane.

---

• So now we know how to represent a complex number on the Argand plane.
• Next we will see how to represent the modulus of a complex number on the Argand plane. It can written in 3 steps:

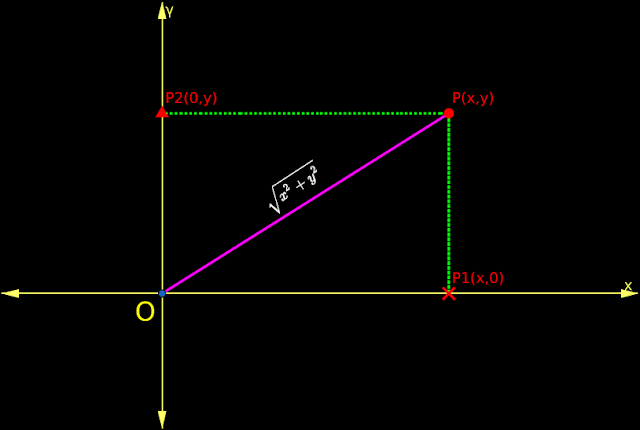
1. In fig.5.2 below, P(x,y) represents the complex number x+yi
    ♦ P₁ is the foot of the perpendicular from P on to the real axis.
    ♦ P₂ is the foot of the perpendicular from P on to the imaginary axis.
    ♦ A magenta line joins the origin O and P

Fig.5.2

2. Now we have a right triangle OP₁P. It is right angled at P₁
• The base of this right triangle is OP₁
    ♦ It’s length is x
• The altitude of this right triangle is PP₁
    ♦ It’s length = length of OP₂ = y
• So the length of OP (hypotenuse) will be $\sqrt{x^2+y^2}$
• The length OP is the distance between P and the origin O
◼ But $\sqrt{x^2+y^2}$ is the modulus of the complex number represented by P
3. So we can write:
    ♦ The distance between P and the origin
    ♦ will be the
    ♦ modulus of the complex number represented by P

---

• So now we know how to represent the modulus of a complex number on the Argand plane.
• Next we will see how to represent the conjugate of a complex number on the Argand plane. It can written in 7 steps:
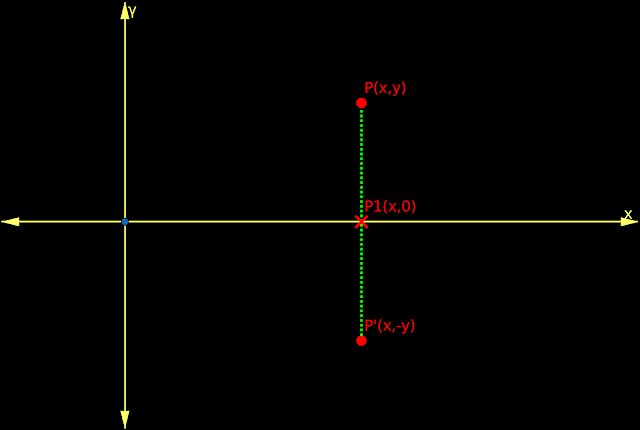
1. In fig.5.3 below, P(x,y) represents the complex number x+yi

Fig.5.3

2. Drop a perpendicular from P on to the real axis.
Let P₁ be the foot of the perpendicular.
3. Extend the line PP₁ downwards upto P` on such a way that, PP₁ = P₁P'
4. Now we can write three points:
(i) Points P and P' lie on opposite sides of the real axis.
(ii) Both P and P' lie on the line perpendicular to the real axis.
(iii) Both P and P` are at equal distances from the real axis.
5. Based on the three points above, we can write:
P' is the mirror image of P. The real axis being the mirror line.
6. The coordinates of P' are: (x,-y)
• So P' represent the complex number x-yi
7. But x-yi is the conjugate of x+yi
• So we can write:
The conjugate of a complex number is represented by the mirror image of that complex number. The real axis being the mirror line.

---

In the next section, we will see polar representation of complex numbers.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com