In the previous section, we completed a discussion on trigonometry. In this chapter we will see Principle of mathematical induction.
Some basic details can be written in 9 steps:
1. Consider the three statements below:
(i) All fruits have seeds.
(ii) Apple have seeds.
(iii) So apple is a fruit.
• The first two are general statements. We use those two general statements to arrive at a specific conclusion. The conclusion is the third statement.
2. Let us see another example:
We have three statements:
(i) All numbers ending in 0 and 5 are divisible by 5
(ii) 75 is a number which ends in 5
(iii) So 75 is divisible by 5
• The first two are general statements. We use those two general statements to arrive at a specific conclusion. The conclusion is the third statement.
3. In each of the above two examples, we used two general statements to arrive at a specific statement. That is., we worked from ‘general’ to ‘specific’. This type of reasoning is known as deductive reasoning.
4. The opposite happens in inductive reasoning. That is., we observe specific cases and based on them, we give a general conclusion.
Let us see an example. As before, there are three statements:
(i) Last year rainy season began on 1st of July.
(ii) The year before that also, rainy season began on 1st of July.
(iii) So every year, rainy season begins on 1st of July.
• The first two are specific statements. We use those two specific statements to arrive at a general conclusion. The conclusion is the third statement.
5. Let us see another example:
(i) Walls of the bedroom are painted blue.
(ii) Walls of the dining room are also painted blue.
(iii) So all rooms of the house are painted blue.
• The first two are specific statements. We use those two specific statements to arrive at a general conclusion. The conclusion is the third statement.
6. In each of the above two examples, we used two specific statements to arrive at a general statement. That is., we worked from ‘specific’ to ‘general’. This type of reasoning is known as inductive reasoning.
7. In inductive reasoning, the conclusion can be challenged. That is., the conclusion may or may not be true.
◼ For example:
• Beginning of rainy season on the 1st of July for two consecutive years, gives no guarantee that, rainy season begins on that day every year.
• Finding blue walls in bedroom and dining room gives no guarantee that, walls of all rooms in the house will be blue.
8. But when we use inductive reasoning in mathematics, we take special precautions so that, the conclusion will be always true.
• The method of inductive reasoning used in mathematics is known as mathematical induction.
9. The basics of mathematical induction can be demonstrated using an example. It can be written in 5 steps:
(i) Fig.4.1(a) below shows some thin tiles placed on their edges. They are placed in a row.
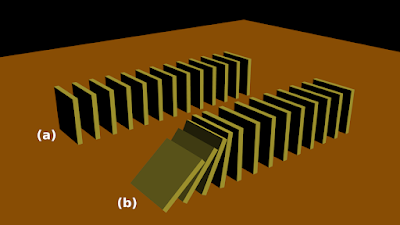 |
| Fig.4.1 |
(ii) If the first tile is pushed, all the tiles will fall. This is shown in fig.b
We want to prove that all tiles have fallen.
(iii) For that we need the following two statements to be true:
♦ (a) The first tile is pushed
♦ (b) If any tile is pushed, the tile coming just after it will fall.
(iv) Note the significance of statement (a):
It is compulsory that, first tile is pushed. Instead of the first tile, if we push any intermediate tile, only those tiles coming after it will fall. We want the entire row to fall. For that, the pushing of the first tile is necessary.
(v) Note the significance of statement (b). It is self explanatory. If this statement is not true, we cannot guarantee that the entire row will fall.
Let us apply the step (9) above to a math problem. It can be written in 4 steps:
1. Consider the sum of n positive integers. A mathematician tells us that, the sum can be calculated using the statement:
$1+2+3+\;.\;.\;.\;+n=\frac{n(n+1)}{2}$
• We want to prove this statement.
2. First we prove that, this statement is true when n = 1
• Put n = 1 in the LHS. We get LHS = 1
• Put n = 1 in the RHS. We get: RHS = $\frac{1(1+1)}{2}=\frac{1 × 2}{2}=1$
• LHS = RHS. So the statement is true when n = 1
◼ This step is called basic step.
3. Next we prove this:
If the statement is true for a positive integer ‘k’, it will be true for the next positive integer (k+1)
• This can be proved in 6 steps:
(i) Put n = k in the LHS. We get: LHS = $1+2+3+\;.\;.\;.\;+k$
• Put n = k in the RHS. We get: RHS = $\frac{k(k+1)}{2}$
• We assume that, this LHS and RHS are equal
(ii) Put n = (k+1) in the LHS. We get: LHS = $1+2+3+\;.\;.\;.\;+k+(k+1)$
• Put n = (k+1) in the RHS. We get: RHS = $\frac{(k+1)[(k+1)+1]}{2}$
(iii) Consider the LHS in (ii). It can be written as: $1+2+3+\;.\;.\;.\;+k+\{(k+1)\}$
• The portion outside the curly brackets, is the LHS in (i)
• We assumed that the LHS in (i) is equal to the RHS in (i)
• So the LHS in (ii) becomes: $\frac{k(k+1)}{2}+\{(k+1)\}$
♦ This can be simplified as:
$\frac{k(k+1)}{2}+\{(k+1)\}~=~\frac{k^2+k+2k+2}{2}~=~\frac{k^2+3k+2}{2}$
(iv) Consider the RHS in (ii).
♦ This RHS can be simplified as:
$\frac{(k+1)[(k+1)+1]}{2}~=~\frac{(k+1)(k+2)}{2}~=~\frac{k^2+3k+2}{2}$
(v) So from (iii) and (iv) we get:
LHS in (ii) = RHS in (ii)
• That means, the statement is true for n = (k+1)
(vi) But remember that, '(k+1)' passed the test because we assumed that the statement is true for n = k
• So we proved that:
If the statement is true for n = k, it will be true for n = (k+1)
◼ This step is called inductive step.
4. So we used basic step in (2) and inductive step in (3)
• In the basic step, we proved that:
The given statement is true when n = 1
• In the inductive step, we proved that:
If the given statement is true for n = k, it will be true for n= (k+1)
• Since both are proved, we can write:
The given statement is true.
Let us see another example. It can be written in 4 steps:
1. Consider the sum of n odd numbers. A mathematician tells us that, the sum will be equal to the square of the ‘number of terms added’. In statement form, it can be written as:
$1+3+5+7+\;.\;.\;.\;+(2n-1)=n^2$
• We want to prove this statement.
2. First we prove that, this statement is true when n = 1
• Put n = 1 in the LHS. We get LHS = 1
• Put n = 1 in the RHS. We get: RHS = $1^2=1$
• LHS = RHS. So the statement is true when n = 1
◼ This step is called basic step.
3. Next we prove this:
If the statement is true for a positive integer ‘k’, it will be true for the next positive integer (k+1)
• This can be proved in 6 steps:
(i) Put n = k in the LHS. We get: LHS = $1+3+5+7+\;.\;.\;.\;+(2k-1)$
• Put n = k in the RHS. We get: RHS = $k^2$
• We assume that, this LHS and RHS are equal
(ii) Put n = (k+1) in the LHS. We get: LHS = $1+3+5+7+\;.\;.\;.\;+(2k-1)+[2(k+1)-1]$
⇒ LHS = $1+3+5+7+\;.\;.\;.\;+(2k-1)+[2k+2-1]$
⇒ LHS = $1+3+5+7+\;.\;.\;.\;+2k-1+2k+1$
• Put n = (k+1) in the RHS. We get: RHS = $(k+1)^2$
(iii) Consider the LHS in (ii). It can be written as: $1+3+5+7+\;.\;.\;.\;+2k-1+\{2k+1\}$
• The portion outside the curly brackets, is the LHS in (i)
• We assumed that the LHS in (i) is equal to the RHS in (i)
• So the LHS in (ii) becomes: $k^2+\{2k+1\}$
♦ This can be simplified as: $(k+1)^2$
(iv) Consider the RHS in (ii). It is also: $(k+1)^2$
(v) So from (iii) and (iv) we get:
LHS in (ii) = RHS in (ii)
• That means, the statement is true for n = (k+1)
(vi) But remember that, '(k+1)' passed the test because we assumed that the statement is true for n = k
• So we proved that:
If the statement is true for n = k, it will be true for n = (k+1)
◼ This step is called inductive step.
4. So we used basic step in (2) and inductive step in (3)
• In the basic step, we proved that:
The given statement is true when n = 1
• In the inductive step, we proved that:
If the given statement is true for n = k, it will be true for n= (k+1)
• Since both are proved, we can write:
The given statement is true.
Let us see one more example. It can be written in 4 steps:
1.
Consider the sum of the squares of n natural numbers. A mathematician tells us that, the sum can be calculated using the statement:
$1^2+2^2+3^2+4^2+\;.\;.\;.\;+n^2=\frac{n(n+1)(2n+1)}{6}$
• We want to prove this statement.
2. First we prove that, this statement is true when n = 1
• Put n = 1 in the LHS. We get LHS = 12 = 1
• Put n = 1 in the RHS. We get:
RHS = $\frac{1(1+1)(2 × 1+1)}{6}$
⇒ RHS = $\frac{1(2)(3)}{6}$ = 1
• LHS = RHS. So the statement is true when n = 1
◼ This step is called basic step.
3. Next we prove this:
If the statement is true for a positive integer ‘k’, it will be true for the next positive integer (k+1)
• This can be proved in 5 steps:
(i) Put n = k in the LHS. We get: LHS = $1^2+2^2+3^2+4^2+\;.\;.\;.\;+k^2$
• Put n = k in the RHS. We get: RHS = $\frac{k(k+1)(2k+1)}{6}$
• We assume that, this LHS and RHS are equal
(ii) Put n = (k+1) in the LHS. We get: LHS = $1^2+2^2+3^2+4^2+\;.\;.\;.\;+k^2+(k+1)^2$
• Put n = (k+1) in the RHS. We get: RHS = $\frac{(k+1)[(k+1)+1][2(k+1)+1]}{6}$
(iii) Consider the LHS in (ii). It can be written as: $1^2+2^2+3^2+4^2+\;.\;.\;.\;+k^2+\{(k+1)^2\}$
• The portion outside the curly brackets, is the LHS in (i)
• We assumed that the LHS in (i) is equal to the RHS in (i)
• So the LHS in (ii) becomes: $\frac{k(k+1)(2k+1)}{6}+\{(k+1)^2\}$
♦ This can be simplified as:
$\frac{k(k+1)(2k+1)}{6}+\{(k+1)^2\}~=~\frac{(k+1)[k(2k+1)]~+~6(k+1)^2}{6}$
${}=~\frac{(k+1)[k(2k+1)~+~6(k+1)]}{6}~=~\frac{(k+1)[2k^2+7k+6]}{6}$
${}=\frac{2k^3+7k^2+6k+2k^2+7k+6}{6}~=~\frac{2k^3+9k^2+13k+6}{6}$
(iv) Consider the RHS in (ii).
♦ This RHS can be simplified as:
$\frac{(k+1)[(k+1)+1][2(k+1)+1]}{6}~=~\frac{(k+1)[k+2][2k+3]}{6}$
${}=~\frac{(k+1)[2k^2+3k+4k+6]}{6}=~\frac{2k^3+3k^2+4k^2+6k+2k^2+3k+4k+6}{6}$
${}=~\frac{2k^3+9k^2+13k+6}{6}$
(v) So from (ii) and (iii) we get:
LHS in (ii) = RHS in (ii)
• That means, the statement is true for n = (k+1)
(vi) But remember that, '(k+1)' passed the test because we assumed that the statement is true for n = k
• So we proved that:
If the statement is true for n = k, it will be true for n = (k+1)
◼ This step is called inductive step.
4. So we used basic step in (2) and inductive step in (3)
• In the basic step, we proved that:
The given statement is true when n = 1
• In the inductive step, we proved that:
If the given statement is true for n = k, it will be true for n = (k+1)
• Since both are proved, we can write:
The given statement is true.
• In the above problem, what the mathematician said, is a statement. We can write two points here:
(i) The statement is: $1^2+2^2+3^2+4^2+\;.\;.\;.\;+n^2=\frac{n(n+1)(2n+1)}{6}$
♦ It is a statement in 'n'
(ii) We can denote the statement as: P(n)
◼ The two points can be combined together as:
$P(n):1^2+2^2+3^2+4^2+\;.\;.\;.\;+n^2=\frac{n(n+1)(2n+1)}{6}$
• Using this information, let us see a condensed form for writing the solution of the above problem.
Problem:
Prove that for any positive integer n, $1^2+2^2+3^2+4^2+\;.\;.\;.\;+n^2=\frac{n(n+1)(2n+1)}{6}$
Solution:
1. For any positive integer n, let P(n) denote the given statement.
Then we can write: $P(n):1^2+2^2+3^2+4^2+\;.\;.\;.\;+n^2=\frac{n(n+1)(2n+1)}{6}$
2. Basic step: (n=1)
$\begin{array}{ll}
\phantom{\Rightarrow~}P(1): &
1^2 & {}={} &
\frac{1(1+1)(2 × 1+1)}{6} & {} \\
{\Rightarrow~} P(1): & 1^2 & {}={} &
\frac{1 × 2 × 3}{6} & {} \\
{} & 1^2 & {}={} & \frac{6}{6} & {} \\
{} & 1 & {}={} & 1 & {} \\
\end{array}$
• So P(n) is true for n=1
3. Inductive step: (n=k) and (n= k+1)
(i) n= k
$P(k): 1^2+2^2+3^2+~.~.~.~+k^2~ =~\frac{k(k+1)(2k+1)}{6}$
• Assume that, this is true.
(ii) n = k+1
$\begin{array}{ll}
\phantom{\Rightarrow~}P(k+1): &
1^2+2^2+3^2+\;.\;.\;.\;+k^2+[(k+1)^2] & {}={} &
\frac{(k+1)[(k+1)+1][2(k+1)+1]}{6} & {} \\
{\Rightarrow~} P(k+1): & \frac{k(k+1)(2k+1)}{6}+[(k+1)^2] & {}={} &
\frac{(k+1)[(k+1)+1][2(k+1)+1]}{6} & {} \\
{}&\color
{green}{\text{[Using result in (i)]}} & {}&{} & {} \\
{\Rightarrow~} P(k+1): & \frac{(k+1)[k(2k+1)]~+~6(k+1)^2}{6} & {}={} & \frac{(k+1)[k+2][2k+3]}{6} & {} \\
{} & \frac{(k+1)[k(2k+1)~+~6(k+1)]}{6} & {}={} & \frac{(k+1)[2k^2+3k+4k+6]}{6} & {} \\
{} & \frac{(k+1)[2k^2+7k+6]}{6} & {}={} & \frac{2k^3+3k^2+4k^2+6k+2k^2+3k+4k+6}{6} & {} \\
{} & \frac{2k^3+7k^2+6k+2k^2+7k+6}{6} & {}={} & \frac{2k^3+9k^2+13k+6}{6} & {} \\
{} & \frac{2k^3+9k^2+13k+6}{6} & {}={} & \frac{2k^3+9k^2+13k+6}{6} & {} \\
\end{array}$
4. Thus P(k+1) is true whenever P(k) is true. Hence by the principle of mathematical induction, P(n) is true for any positive integer n.
In the next section, we will see problems involving inequality.
Copyright©2022 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment