Chapter 3.21 -The Cosine Formula

In the previous section, we completed a discussion on sine formula. We saw that, we will not be able to apply the sine rule when:
(i) We are given two sides and the angle included between those two given sides.
(ii) We are given all the three sides but no angles.
• In such situations, we can use the cosine formula.

• We can use the same notations and figures 3.39, 40 and 41 that we saw in the previous section. So we will show them again.

• Consider the triangle ABC in fig.3.39 below.
• For this triangle, we can define three angles:
   ♦ Angle A is the angle between sides AB and AC 
   ♦ Angle B is the angle between sides BA and BC 
   ♦ Angle C is the angle between sides CA and CB 
• We can define three sides also:
   ♦ a is the length of the side BC (The side opposite angle A)
   ♦ b is the length of the side AC (The side opposite angle B)
   ♦ c is the length of the side AB (The side opposite angle C)

Fig.3.39

◼ Based on the above notations, we can write the cosine formula as:

a² = b² + c² - 2bc cos A
b² = c² + a² - 2ca cos B
c² = a² + b² - 2ab cos C

• For proving this formula, we will analyze an obtuse triangle and an acute triangle.

• An obtuse triangle is that triangle in which one angle is obtuse and the remaining two are acute. (Remember that, no triangle can have more than one obtuse angles). • An acute triangle is that triangle in which all three angles are acute.

• Both triangles can be analyzed using the same steps.
• When the formula is proved for both those types of triangles, we can confidently apply it to any triangle.

The proof can be written in 8 steps:
1. Dropping perpendiculars from the top vertex:
• For the obtuse triangle in fig.3.40(i) below, the perpendicular dropped from the top vertex B can meet the base AC only if we extend the base a bit towards the right.

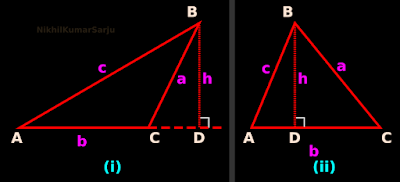Fig.3.40

• For the acute triangle in fig.3.40(ii), the perpendicular dropped from the top vertex B can meet the base AC with out any difficulty.
2. Name of the perpendiculars:
• For both the triangles, the perpendiculars are named as BD.
   ♦ D is the foot of the perpendicular.
3. Length of the perpendiculars:
• For both the triangles, the length of the perpendiculars are denoted as h.
   ♦ h is called the altitude of the triangle
4. Writing a in terms of b, c and A:
I. In fig.3.40(i), considering right triangle BCD, we have:
BC² = BD² + CD²
⇒ BC² = BD² + (AD - AC)²
⇒ BC² = BD² + AD² + AC² - 2AD.AC
⇒ BC² = AB² + AC² - 2AD.AC
(In the right triangle ABD, BD² + AD² = AB²)
⇒ BC² = AB² + AC² - 2AC.AB cos A
(In the right triangle ABD, AD = AB cos A)
⇒ a² = c² + b² - 2b.c cos A
⇒ a² = b² + c² - 2bc cos A
II. In fig.3.40(ii) also, we can obtain the same result by modifying the steps slightly. Considering right triangle BCD, we have:
BC² = BD² + CD²
⇒ BC² = BD² + (AC - AD)²
⇒ BC² = BD² + AC² + AD² - 2AC.AD
⇒ BC² = BD² + AD² + AC² - 2AC.AD
⇒ BC² = AB² + AC² - 2AD.AC
(In the right triangle ABD, BD² + AD² = AB²)
⇒ BC² = AB² + AC² - 2AC.AB cos A
(In the right triangle ABD, AD = AB cos A)
⇒ a² = c² + b² - 2b.c cos A
⇒ a² = b² + c² - 2bc cos A
◼ We see that:
Relation between a, b, c and cos A is the same for both the triangles.
So the relation is applicable to any triangle. 
5. In the above steps, we did not come across angles B and C. The following steps (6) and (7) will help us to derive a relation involving angle B.
6. Fig.3.41 below shows the same triangles. But this time, the perpendiculars are drawn from vertex C.

Fig.3.41

7. Writing b in terms of c, a and B:
I. In fig.3.40(i), considering right triangle BCD, we have:
AC² = AD² + CD²
⇒ AC² = (AB - BD)² + CD²
⇒ AC² = AB² + BD² - 2AB.BD + CD²
⇒ AC² = AB² + (BD² + CD²) - 2AB.BD
⇒ AC² = AB² + BC² - 2AB.BD
(In the right triangle BCD, BD² + CD² = BC²)
⇒ AC² = AB² + BC² - 2AB.BC cos B
(In the right triangle BCD, BD = BC cos B)
⇒ b² = c² + a² - 2c.a cos B
⇒ b² = c² + a² - 2ca cos B
II. In fig.3.40(ii) also, we can obtain the same result without any modification of the steps. This is because, the arrangements of inner triangles in both cases are similar. The steps will be exactly the same as in 7.I. We will get:
b² = c² + a² - 2ca cos B
◼ We see that:
Relation between b, c, a and cos B is the same for both the triangles.
So the relation is applicable to any triangle.
8. By drawing perpendicular from the vertex A, we will be able to prove the third result:
c² = a² + b² - 2ab cos C
• The reader may write all the steps in his/her own note books.
Hint: The figures will be as shown in fig.3.43 below:

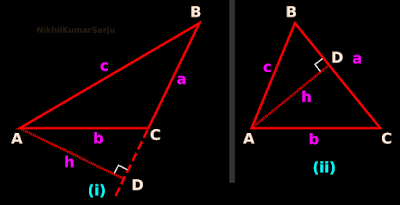Fig.3.43

---

Let us see some examples:
Example 1:
Fig.3.44(i) below shows a triangle ABC in which two sides and an included angle are given. We are asked to find the remaining one side and the remaining two angles.

Fig.3.44

Solution:
1. We have the initial table:
$\begin{eqnarray}
A = -- \,&{|}& B = --&{|}& C = 95 \\
a = 16.84 \,&{|}& b = 11.17 &{|}& c = -- \
\end{eqnarray}$
2. Using the cosine formula, we have:
c² = a² + b² - 2ab cos C
• Substituting the known values, we get:
c² = 16.84² + 11.17² - 2 × 16.84 × 11.17 × cos 95
⇒ c² = 16.84² + 11.17² - 2 × 16.84 × 11.17 × -0.0871 = 441.143
⇒ c = ± 21.003
• Length cannot be -ve. So we get: c = 21 cm
• So the table becomes:
$\begin{eqnarray}
A = -- \,&{|}& B = --&{|}& C = 95 \\
a = 16.84 \,&{|}& b = 11.17 &{|}& c = 21 \
\end{eqnarray}$
3. Once we get this additional information, it is always easier to proceed using sine formula.
$\begin{eqnarray}
&{}& \frac{\sin C}{c}=\frac{\sin B}{b} \\
&\Rightarrow& \frac{\sin 95}{21}=\frac{\sin B}{11.17} \\
&\Rightarrow& \sin B=0.5299 \\
&\Rightarrow& B=31.99=32^{\text{o}} \
\end{eqnarray}$
• Consider the identity: sin x = sin (180-x). We get:
    ♦ sin 32 = sin (180-32) = sin 148 = 0.6952
    ♦ That means, sin A = 0.5299 will give two values for A: 32 and 148
• In our present case, angle at C is already an obtuse angle. No triangle can have two obtuse angles. So the appropriate value for A is 32
• Now the table becomes:
$\begin{eqnarray}
A = -- \,&{|}& B = 32&{|}& C = 95 \\
a = 16.84 \,&{|}& b = 11.17 &{|}& c = 21 \
\end{eqnarray}$
4. Using the sine formula again, we have:
$\frac{\sin A}{a}=\frac{\sin C}{c}$
$\begin{eqnarray}
&{}& \frac{\sin A}{16.84}=\frac{\sin 95}{21} \\
&\Rightarrow& A=53.02=53^{\text{o}} \
\end{eqnarray}$
• Here also we must discard (180-53) because, angle at C is already obtuse.
• Check: A = [180 - (95+32)=53]
• So the final table is:
$\begin{eqnarray}
A = 53 \,&{|}& B = 32&{|}& C = 95 \\
a = 16.84 \,&{|}& b = 11.17 &{|}& c = 21 \
\end{eqnarray}$
5. Note that in this problem, the only option to start calculations, is by using cosine formula. We cannot start with sine formula because, we are given two sides and the included angle.

---

Let us solve this problem using Cosine formula alone.
1. We have the initial table:
$\begin{eqnarray}
A = -- \,&{|}& B = --&{|}& C = 95 \\
a = 16.84 \,&{|}& b = 11.17 &{|}& c = -- \
\end{eqnarray}$
2. Using the Cosine formula, we have:
c² = a² + b² - 2ab cos C
• Substituting the known values, we get:
c² = 16.84² + 11.17² - 2 × 16.84 × 11.17 × cos 95
⇒ c² = 16.84² + 11.17² - 2 × 16.84 × 11.17 × -0.0871 = 441.143
⇒ c = ± 21.003
• Length cannot be -ve. So we get: c = 21 cm
• So the table becomes:
$\begin{eqnarray}
A = -- \,&{|}& B = --&{|}& C = 95 \\
a = 16.84 \,&{|}& b = 11.17 &{|}& c = 21 \
\end{eqnarray}$
3. Using the Cosine formula again, we have:
a² = b² + c² - 2bc cos A
• Substituting the known values, we get:
16.84² = 11.17² + 21² - 2 × 11.17 × 21 × cos A
⇒ cos A = 0.6013
⇒ A = 53.03 = 53
• Consider the identity: cos x = cos (360-x). We get:
    ♦ cos 53.03 = cos (360-53) = cos 307 = 0.6013
    ♦ That means, cos C = 0.6013 will give two values for C: 53 and 307
• But 307 is not acceptable because, it is greater than 180
• So the table becomes:
$\begin{eqnarray}
A = 53 \,&{|}& B = --&{|}& C = 95 \\
a = 16.84 \,&{|}& b = 11.17 &{|}& c = 21 \
\end{eqnarray}$
4. Using the Cosine formula again, we have:
b² = a² + c² - 2ac cos B
• Substituting the known values, we get:
11.17² = 16.84² + 21² - 2 × 16.84 × 21 × cos B
⇒ cos B = 0.8481
⇒ B = 31.99 = 32
• Consider the identity: cos x = cos (360-x). We get:
    ♦ cos 32 = cos (360-32) = cos 328 = 0.8481
    ♦ That means, cos C = 0.8481 will give two values for C: 32 and 328
• But 328 is not acceptable because, it is greater than 180
• So the table becomes:
$\begin{eqnarray}
A = 53.03 \,&{|}& B = 32&{|}& C = 95 \\
a = 16.84 \,&{|}& b = 11.17 &{|}& c = 21 \
\end{eqnarray}$

Example 2:
Fig.3.44(ii) above shows a triangle ABC in which all three sides are given. We are asked to find the three angles.
Solution:
1. We have the initial table:
$\begin{eqnarray}
A = -- \,&{|}& B = --&{|}& C = -- \\
a = 3.6 \,&{|}& b = 3.04 &{|}& c = 5.1 \
\end{eqnarray}$
2. Using the cosine formula, we have:
$\cos A=\frac{b^2+c^2-a^2}{2bc}$
• Substituting the known values, we get:
$\cos A=\frac{3.04^2+5.1^2-3.6^2}{2\times 3.04 \times 5.1}$
⇒ A = 44.04
• So the table becomes:
$\begin{eqnarray}
A = 44.04 \,&{|}& B = --&{|}& C = -- \\
a = 3.6 \,&{|}& b = 3.04 &{|}& c = 5.1 \
\end{eqnarray}$
3. Once we get this additional information, it is always easier to proceed using sine formula.
$\begin{eqnarray}
&{}& \frac{\sin A}{a}=\frac{\sin B}{b} \\
&\Rightarrow& \frac{\sin 44.04}{3.6}=\frac{\sin B}{3.04} \\
&\Rightarrow& \sin B=0.5870 \\
&\Rightarrow& B=35.96^{\text{o}} \
\end{eqnarray}$
• Consider the identity: sin x = sin (180-x). We get:
    ♦ sin 35.96 = sin (180-35.96) = sin 144.04 = 0.5870
    ♦ That means, sin B = 0.5870 will give two values for B: 35.96 and 144.04
• In our present case, we have already calculated A as 44.04
    ♦ If we choose B = 144.04, then (A+B) will become (44.04+144.04) = 188.08
    ♦ The sum cannot be greater than 180.
    ♦ So we must discard 144.04 and choose 35.96
• Now the table becomes:
$\begin{eqnarray}
A = 44.04 \,&{|}& B = 35.96&{|}& C = -- \\
a = 3.6 \,&{|}& b = 3.04 &{|}& c = 5.1 \
\end{eqnarray}$
4. Using the sine formula again, we have:
$\frac{\sin A}{a}=\frac{\sin C}{c}$
$\begin{eqnarray}
&{}& \frac{\sin 44.04}{3.6}=\frac{\sin C}{5.1} \\
&\Rightarrow& \sin C=0.9848 \\
&\Rightarrow& C=80^{\text{o}} \
\end{eqnarray}$
• Consider the identity: sin x = sin (180-x). We get:
    ♦ sin 80 = sin (180-80) = sin 100 = 0.9848
    ♦ That means, sin C = 0.9848 will give two values for C: 80 and 100
• In our present case, we have already calculated A and B as 44.04 and 35.96
    ♦ If we choose C = 80, then (A+B+C) will become (44.04+35.96+80) =160
    ♦ The sum cannot be less than 180.
    ♦ So we must discard 80 and choose 100
• Check: C = [180 - (44.04+35.96)=100]
• So the final table is:
$\begin{eqnarray}
A = 44.04 \,&{|}& B = 35.95&{|}& C = 100 \\
a = 3.6 \,&{|}& b = 3.04 &{|}& c = 5.1 \
\end{eqnarray}$
5. Note that in this problem, the only option to start calculations, is by using cosine formula. We cannot start with sine formula because, we are given the three sides.

---

Let us solve this problem using Cosine formula alone.
1. We have the initial table:
$\begin{eqnarray}
A = -- \,&{|}& B = --&{|}& C = -- \\
a = 3.6 \,&{|}& b = 3.04 &{|}& c = 5.1 \
\end{eqnarray}$
2. Using the Cosine formula, we have:
$\cos A=\frac{b^2+c^2-a^2}{2bc}$
• Substituting the known values, we get:
$\cos A=\frac{3.04^2+5.1^2-3.6^2}{2\times 3.04 \times 5.1}$
⇒ A = 44.04
• So the table becomes:
$\begin{eqnarray}
A = 44.04 \,&{|}& B = --&{|}& C = -- \\
a = 3.6 \,&{|}& b = 3.04 &{|}& c = 5.1 \
\end{eqnarray}$
3. Using the Cosine formula again, we have:
b² = a² + c² - 2ac cos B
• Substituting the known values, we get:
3.04² = 3.6² + 5.1² - 2 × 3.6 × 5.1 × cos B
⇒ cos B = 0.8096
⇒ B = 35.94
• Consider the identity: cos x = cos (360-x). We get:
    ♦ cos 35.94 = cos (360-35.94) = cos 324.06 = 0.8096
    ♦ That means, cos B = 0.8096 will give two values for C: 35.94 and 324.06
• But 324.06 is not acceptable because, it is greater than 180
• So the table becomes:
$\begin{eqnarray}
A = 44.04 \,&{|}& B = 35.94&{|}& C = -- \\
a = 3.6 \,&{|}& b = 3.04 &{|}& c = 5.1 \
\end{eqnarray}$
4. Using the Cosine formula again, we have:
c² = a² + b² - 2ab cos C
• Substituting the known values, we get:
5.1² = 3.6² + 3.04² - 2 × 3.6 × 3.04 × cos C
⇒ cos C = -0.1739
⇒ C = 100.02 = 100
• Consider the identity: cos x = cos (360-x). We get:
    ♦ cos 100 = cos (360-100) = cos 260 = -0.1739
    ♦ That means, cos C = -0.1739 will give two values for C: 100 and 260
• But 260 is not acceptable because, it is greater than 180
• So the table becomes:
$\begin{eqnarray}
A = 44.04 \,&{|}& B = 35.94&{|}& C = 100 \\
a = 3.6 \,&{|}& b = 3.04 &{|}& c = 5.1 \
\end{eqnarray}$

---

In the next section, we will see Napier's Analogies.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com