Chapter 20 - Determinants

In the previous section, we completed a discussion on matrices. In this chapter, we will see determinants.

Some basics about determinants can be written in 6 steps:
1. Consider any square matrix A.
• Using some simple steps, we can find a unique number related to that matrix.
• This number is called determinant of A.
2. Symbolically, we denote this number as |A|.
    ♦ It should not be read as modulus of A.
    ♦ It should be read as determinant of A.
3. There are two more ways for denoting this number:
   ♦ det(A)
   ♦ Δ
4. Let us see an example:
If $A = \left[\begin{array}{r}               
a    &{    b    }    \\
c    &{    d    }    \\
\end{array}\right]$, then $|A| ~=~ \left|\begin{array}{r}              
a    &{    b    }    \\
c    &{    d    }    \\
\end{array}\right|
~=~ \text{det}(A)$
 
5. Only square matrices have determinants.
6. The determinant can be a real number or a complex number.
• In this chapter we will be dealing with only those determinants, which are real numbers.

---

Method for finding the determinant of a 2 × 2 matrix

• This can be written in 3 steps:
1. Let A = $\left[\begin{array}{r}               
a_{11}    &{    a_{12}    }    \\
a_{21}    &{    a_{22}    }    \\
\end{array}\right]$
2. Then det(A) = |A| = $\left|\begin{array}{r}               
a_{11}    &{    a_{12}    }    \\
a_{21}    &{    a_{22}    }    \\
\end{array}\right|~=~a_{11}a_{22}~-~a_{21}a_{12}$
3. Note that, there are two terms in the determinant.
• Each term is a product of two elements, taken in a specified order. This order is indicated by the yellow arrows in fig.20.1 below:

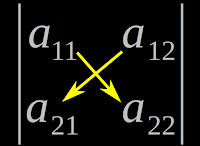Fig.20.1

• After calculating the two terms, we subtract the second term from the first.

---

Solved example 20.1
Evaluate $\left|\begin{array}{r}               
2    &{    4    }    \\
-1    &{    2    }    \\
\end{array}\right|$
Solution:
$\left|\begin{array}{r}               
2    &{    4    }    \\
-1    &{    2    }    \\
\end{array}\right|$ = 2(2) − 4(−1) = 4+4 = 8

Solved example 20.2
Evaluate $\left|\begin{array}{r}               
x    &{    x+1    }    \\
x-1    &{    x    }    \\
\end{array}\right|$
Solution:
$\begin{array}{ll} {~\color{magenta}    1    }    &{{}}    &{\left|\begin{array}{c}                x    &{    x+1    }    \\ x-1    &{    x    }    \\ \end{array}\right|}    & {~=~}    &{x(x)-(x+1)(x-1)}    \\
{~\color{magenta}    2    }    &{{}}    &{{}}    & {~=~}    &{x^2-(x^2 – 1)}    \\
{~\color{magenta}    3    }    &{{}}    &{{}}    & {~=~}    &{x^2- x^2 + 1}    \\
{~\color{magenta}    4    }    &{{}}    &{{}}    & {~=~}    &{1}    \\
\end{array}$

---

Method for finding the determinant of a 3 × 3 matrix

• Consider the 3 × 3 matrix A = $\left[\begin{array}{r}                           
a_{11}     &{    a_{12}     }    &{    a_{13}      }    \\
a_{21}      &{    a_{22}     }    &{    a_{23}      }    \\
a_{31}      &{    a_{32}       }    &{    a_{33}        }    \\
\end{array}\right]$
• We want $\left|\begin{array}{r}                           
a_{11}     &{    a_{12}     }    &{    a_{13}      }    \\
a_{21}      &{    a_{22}     }    &{    a_{23}      }    \\
a_{31}      &{    a_{32}       }    &{    a_{33}        }    \\
\end{array}\right|$
• Let us use the first row R₁. It can be done in 4 steps:
Step 1:
• Take the first element of R₁, which is a₁₁.
• Delete the row in which a₁₁ is situated.
• This is indicated by the yellow rectangle in fig,20.2(a) below:

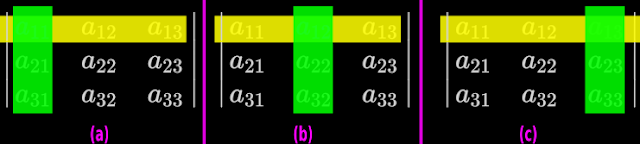Fig.20.2

• Delete the column in which a₁₁ is situated.
• This is indicated by the green rectangle in fig,20.2(a) above.
• Now write the following three items:
(i) The 2 × 2 determinant obtained by deleting the row and column.
(ii) Element which is under consideration. Here it is a₁₁.
(iii) (-1)^s, where s is the sum of the suffices of a₁₁.
So (-1)^s = (-1)¹⁺¹.
• Finally, multiply the three items together. We get:
$(-1)^{1+1} \times a_{11} \times \left|\begin{array}{r}               
a_{22}    &{    a_{23}    }    \\
a_{32}    &{    a_{33}    }    \\
\end{array}\right|$   

Step 2:
• Take the second element of R₁, which is a₁₂.
• Delete the row in which a₁₂ is situated.
• This is indicated by the yellow rectangle in fig,20.2(b) above.
• Delete the column in which a₁₂ is situated.
• This is indicated by the green rectangle in fig,20.2(b) above.
• Now write the following three items:
(i) The 2 × 2 determinant obtained by deleting the row and column.
(ii) Element which is under consideration. Here it is a₁₂.
(iii) (-1)^s, where s is the sum of the suffices of a₁₂.
So (-1)^s = (-1)¹⁺².
• Finally, multiply the three items together. We get:
$(-1)^{1+2} \times a_{12} \times \left|\begin{array}{r}               
a_{21}    &{    a_{23}    }    \\
a_{31}    &{    a_{33}    }    \\
\end{array}\right|$   

Step 3:
• Take the third element of R₁, which is a₁₃.
• Delete the row in which a₁₃ is situated.
• This is indicated by the yellow rectangle in fig,20.2(c) above.
• Delete the column in which a₁₃ is situated.
• This is indicated by the green rectangle in fig,20.2(c) above.
• Now write the following three items:
(i) The 2 × 2 determinant obtained by deleting the row and column.
(ii) Element which is under consideration. Here it is a₁₃.
(iii) (-1)^s, where s is the sum of the suffices of a₁₃.
So (-1)^s = (-1)¹⁺³.
• Finally, multiply the three items together. We get:
$(-1)^{1+3} \times a_{13} \times \left|\begin{array}{r}               
a_{21}    &{    a_{22}    }    \\
a_{31}    &{    a_{32}    }    \\
\end{array}\right|$

Step 4:
• This is the final step. Here we add the results obtained in the above three steps.
• The sum thus obtained is the determinant of A. We can write:

◼ The above process by which we apply the four steps to find the determinant of order 3, is known as expansion along R₁.

---

In the next section, we will see the process of finding the determinant by expansion along R₂.

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com