Chapter 10.2 - Angle Between Two Lines

In the previous section, we saw slope and inclination of lines. In this section, we will see angle between two lines.

• Consider two lines lying in a plane. One of the following two possibilities will always occur:
(i) The two lines are parallel.
   ♦ They will never intersect.
(ii) The two lines are non-parallel
   ♦ Two non-parallel lines will surely intersect at a point.
• Two non-parallel lines may be lying far away from each other. But if we extend them suitably, they will surely intersect at a point.
• When two lines intersect, an angle will be formed between them.
• It is possible to find that angle using the slopes of the lines. Let us see how it is done. It can be written in 5 steps:

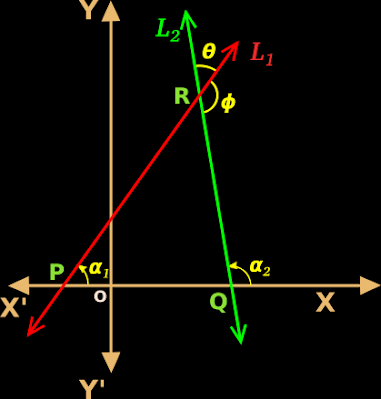
1. Fig.10.8(a) below shows two non-vertical lines L₁ and L₂.
    ♦ L₁ has an inclination of 𝛼
    ♦ L₂ has an inclination of β
    ♦ The slope of L₁ is m₁
    ♦ The slope of L₂ is m₂

Fig.10.8

2. Formation of triangle PQR:
    ♦ L₁ and L₂ intersect at R.
    ♦ L₁ intersect the x-axis at P
    ♦ L₂ intersect the x-axis at Q
• Thus we get a right angled triangle PQR
3. Formation of two angles:
• L₁ and L₂ intersect at R. The angle formed at R is marked as 𝜃.
• When 𝜃 is formed, another angle ɸ is also formed at the point of intersection.
• We see that: 𝜃 + ɸ = 180^o
4. Relation between 𝛼₁, 𝛼₂ and 𝜃:
• 𝛼₂ is an exterior angle of the triangle PQR
• For this exterior angle 𝛼₂, the angles 𝛼₁ and ∠PRQ are remote interior angles.
    ♦ ∠PRQ and 𝜃 are opposite angles
    ♦ So ∠PRQ = 𝜃
• Then we get: 𝛼₂ = 𝛼₁ + 𝜃
Which is same as: 𝜃 = 𝛼₂ - 𝛼₁
• This result can be used to find a relation between 𝜃, m₁ and m₂:

$\begin{array}{ll}
{}&{\theta}
&{}={}& {\alpha_2 - \alpha_1}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\tan (\alpha_2 - \alpha_1)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{\tan \alpha_2~-~\tan \alpha_1}{1~+~\tan \alpha_1 \tan \alpha_2}}
&{\color {green}{\text{- - - (a) }}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{m_2~-~m_1}{1~+~m_1 m_2}}
&{\color {green}{\text{- - - (b) }}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
(i) Line marked as (a):
See identity 11 in the list of identities.
(ii) Line marked as (b):
   ♦ tan 𝛼₁ is m₁
   ♦ tan 𝛼₂ is m₂


5. Using this relation, we can find 𝜃

---

Let us see an example:
Solved example 2
Two lines lying in the XY-plane have slopes $\frac{1}{2}$ and 3. Find the angle between them.
Solution:
1. Let m₁ = $\frac{1}{2}$ and m₂ = 3
• We are asked to find 𝜃
2. We have the equation: $\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\tan \theta}
&{}={}& {\frac{3~-~\frac{1}{2}}{1~+~\frac{1}{2}  × 3}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{6 ~-~1}{2~+~3}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{5}{5}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {1}
&{} \\

\end{array}$

3. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
2. Given that: tan 𝜃 = 1
• We know that 45^o is a principal solution.
• That means, we can put 45^o in place of 𝜃.
3. We will now find another principal solution.
• We have seen that, 𝜃 = 45^o is a principal solution.
• When the input 𝜃 is 45^o, the left side becomes tan 45^o
• This gives us: tan 𝜃 = tan 45^o = 1
• We want another angle such that, it's tangent is also 1
• Such an angle can be calculated using identities 9.f and 9.e [See the list of identities]: tan (π+x) = tan x
• We get:
tan 45^o = tan (180^o + 45^o) = tan 225^o
• So we can write:
tan 𝜃 = tan 45^o = tan 225^o
• Picking the first and last items, we get:
𝜃 = 225^o
   ♦ 225^o is greater than 0^o
   ♦ 225^o is less than 360^o  also.
   ♦ So it can be accepted as a principal solution.
• Thus we have two principal solutions for 𝜃:
𝜃 = 45^o and 𝜃 = 225^o
4. Fig.10.9 below shows how the two angles 45^o and 225^o are related to the given lines.

Fig.10.9

• The red line has a slope of $\frac{1}{2}$
Two convenient points points A and B are marked on this line.
• The green line has a slope of 3
Two convenient points points C and D are marked on this line.
• The two lines intersect at E
• ∠AEC (measured in the anti-clockwise direction) is the angle between the two lines. It's value is 45^o
• ∠BEC (measured in the anti-clockwise direction) is also an angle between the two lines. It's value is (180 + 45) = 225^o
5. In step (1), we took m₁ = $\frac{1}{2}$ and m₂ = 3.
• Since the order is not specified, we can take the reverse order also.
   ♦ That is., we interchange m₁ and m₂.
• Let us see if there is any change in the angles when we do the interchange. The following steps from (6) to (11) will give us the angles.
6. Let m₁ = 3 and m₂ = $\frac{1}{2}$
• We are asked to find 𝜃
7. We have the equation: $\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\tan \theta}
&{}={}& {\frac{\frac{1}{2}~-~3}{1~+~ 3 × \frac{1}{2}}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{1~-~6}{2~+~3}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {-\frac{5}{5}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {-1}
&{} \\

\end{array}$

8. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
9. Given that: tan 𝜃 = -1
• We know that 135^o is a principal solution.
• That means, we can put 135^o in place of 𝜃.
10. We will now find another principal solution.
• We have seen that, 𝜃 = 135^o is a principal solution.
• When the input 𝜃 is 135^o, the left side becomes tan 135^o
• This gives us: tan 𝜃 = tan 135^o = -1
• We want another angle such that, it's tangent is also -1
• Such an angle can be calculated using identities 9.f and 9.e: tan (π+x) = tan x
• We get:
tan 135^o = tan (180^o + 135^o) = tan 315^o
• So we can write:
tan 𝜃 = tan 135^o = tan 315^o
• Picking the first and last items, we get:
𝜃 = 315^o
   ♦ 315^o is greater than 0^o
   ♦ 315^o is less than 360^o  also.
   ♦ So it can be accepted as a principal solution.
• Thus we have two principal solutions for 𝜃:
𝜃 = 135^o and 𝜃 = 315^o
11. Fig.10.10 below shows how the two angles 135^o and 315^o are related to the given lines.

Fig.10.10

• The red line has a slope of $\frac{1}{2}$
Two convenient points points A and B are marked on this line.
• The green line has a slope of 3
Two convenient points points C and D are marked on this line.
• The two lines intersect at E
• ∠DEA (measured in the anti-clockwise direction) is the angle between the two lines. It's value is 135^o
• ∠DEB (measured in the anti-clockwise direction) is also an angle between the two lines. It's value is (∠DEA + ∠AEC + ∠CEB) = (135 + 45 +135) = 315^o
12. The figs.10.9 and 10.10 are exactly the same. They appear different because, in the first fig, we marked the acute angle between the given lines. In the second fig., we marked the obtuse angle. 
• Based on this, we can write a conclusion. It can be written in 3 steps:
(i) First we find tan 𝜃 using the equation:
$\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
(ii) If tan 𝜃 obtained is +ve, the 𝜃 so obtained is the acute angle between the given lines.
(iii) If tan 𝜃 obtained is -ve, the 𝜃 so obtained is the obtuse angle between the given lines.

---

Solved example 3
Two lines lying in the XY-plane have slopes $\frac{1}{2}$ and $-\frac{1}{3}$. Find the angle between them.
Solution:
1. Let m₁ = $\frac{1}{2}$ and m₂ = $-\frac{1}{3}$
• We are asked to find 𝜃
2. We have the equation: $\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\tan \theta}
&{}={}& {\frac{-\frac{1}{3}~-~\frac{1}{2}}{1~+~\frac{1}{2}  × -\frac{1}{3}}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{-2 ~-~3}{6~-~1}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{-5}{5}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {-1}
&{} \\

\end{array}$

3. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
2. Given that: tan 𝜃 = -1
• We know that 135^o is a principal solution.
• That means, we can put 135^o in place of 𝜃.
3. We will now find another principal solution.
• We have seen that, 𝜃 = 135^o is a principal solution.
• When the input 𝜃 is 135^o, the left side becomes tan 135^o
• This gives us: tan 𝜃 = tan 135^o = -1
• We want another angle such that, it's tangent is also -1
• Such an angle can be calculated using identities 9.f and 9.e [See the list of identities]: tan (π+x) = tan x
• We get:
tan 135^o = tan (180^o + 135^o) = tan 315^o
• So we can write:
tan 𝜃 = tan 135^o = tan 315^o
• Picking the first and last items, we get:
𝜃 = 315^o
   ♦ 315^o is greater than 0^o
   ♦ 315^o is less than 360^o  also.
   ♦ So it can be accepted as a principal solution.
• Thus we have two principal solutions for 𝜃:
𝜃 = 135^o and 𝜃 = 315^o
4. Fig.10.11 below shows how the two angles 135^o and 315^o are related to the given lines.

Fig.10.11

• The red line has a slope of $\frac{1}{2}$
Two convenient points points A and B are marked on this line.
• The green line has a slope of $-\frac{1}{3}$
Two convenient points points C and D are marked on this line.
• The two lines intersect at E
• ∠BEC (measured in the anti-clockwise direction) is the angle between the two lines. It's value is 135^o
• ∠BED (measured in the anti-clockwise direction) is also an angle between the two lines. It's value is (∠BEA + ∠AED) = (180 + 135) = 315^o
5. In step (1), we took m₁ = $\frac{1}{2}$ and m₂ = $-\frac{1}{3}$.
• Since the order is not specified, we can take the reverse order also.
• Since the order is not specified, we can take the reverse order also.
   ♦ That is., we interchange m₁ and m₂.
• Let us see if there is any change in the angles when order is reversed. The following steps from (6) to (11) will give us the angles.
6. Let m₁ = $-\frac{1}{3}$ and m₂ = $\frac{1}{2}$
• We are asked to find 𝜃
7. We have the equation: $\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\tan \theta}
&{}={}& {\frac{\frac{1}{2}~-~-\frac{1}{3}}{1~+~ -\frac{1}{3} × \frac{1}{2}}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{3~+~2}{6~-~1}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{5}{5}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {1}
&{} \\

\end{array}$

8. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
9. Given that: tan 𝜃 = 1
• We know that 45^o is a principal solution.
• That means, we can put 45^o in place of 𝜃.
10. We will now find another principal solution.
• We have seen that, 𝜃 = 45^o is a principal solution.
• When the input 𝜃 is 45^o, the left side becomes tan 45^o
• This gives us: tan 𝜃 = tan 45^o = 1
• We want another angle such that, it's tangent is also 1
• Such an angle can be calculated using identities 9.f and 9.e: tan (π+x) = tan x
• We get:
tan 45^o = tan (180^o + 45^o) = tan 225^o
• So we can write:
tan 𝜃 = tan 45^o = tan 225^o
• Picking the first and last items, we get:
𝜃 = 225^o
   ♦ 225^o is greater than 0^o
   ♦ 225^o is less than 360^o  also.
   ♦ So it can be accepted as a principal solution.
• Thus we have two principal solutions for 𝜃:
𝜃 = 45^o and 𝜃 = 225^o
11. Fig.10.12 below shows how the two angles 45^o and 225^o are related to the given lines.

Fig.10.12

• The red line has a slope of $\frac{1}{2}$
Two convenient points points A and B are marked on this line.
• The green line has a slope of $-\frac{1}{3}$
Two convenient points points C and D are marked on this line.
• The two lines intersect at E
• ∠CEA (measured in the anti-clockwise direction) is the angle between the two lines. It's value is 45^o
• ∠CEB (measured in the anti-clockwise direction) is also an angle between the two lines. It's value is (CEA + 180) = (45 +180) = 225^o
12. The figs.10.11 and 10.12 are exactly the same. They appear different because, in the first fig, we marked the obtuse angle between the given lines. In the second fig., we marked the acute angle. 
• Based on this, we can write the same conclusion that we wrote in the previous solved example. It can be written in 3 steps:
(i) First we find tan 𝜃 using the equation:
$\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
(ii) If tan 𝜃 obtained is +ve, the 𝜃 so obtained is the acute angle between the given lines.
(iii) If tan 𝜃 obtained is -ve, the 𝜃 so obtained is the obtuse angle between the given lines.

---

In the next section, we will see a few more solved examples.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com