Chapter 10.2 - Angle Between Two Lines

In the previous section, we saw slope and inclination of lines. In this section, we will see angle between two lines.

• Consider two lines lying in a plane. One of the following two possibilities will always occur:
(i) The two lines are parallel.
   ♦ They will never intersect.
(ii) The two lines are non-parallel
   ♦ Two non-parallel lines will surely intersect at a point.
• Two non-parallel lines may be lying far away from each other. But if we extend them suitably, they will surely intersect at a point.
• When two lines intersect, an angle will be formed between them.
• It is possible to find that angle using the slopes of the lines. Let us see how it is done. It can be written in 5 steps:

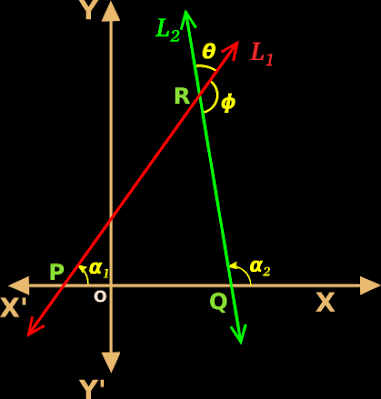
1. Fig.10.8(a) below shows two non-vertical lines L₁ and L₂.
    ♦ L₁ has an inclination of 𝛼
    ♦ L₂ has an inclination of β
    ♦ The slope of L₁ is m₁
    ♦ The slope of L₂ is m₂

Fig.10.8

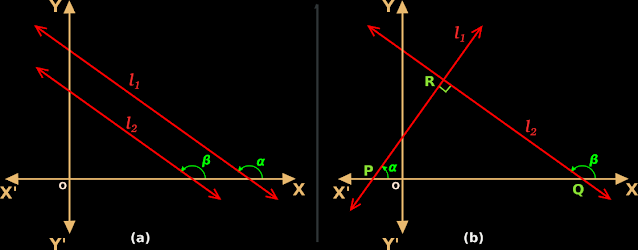
2. Formation of triangle PQR:
    ♦ L₁ and L₂ intersect at R.
    ♦ L₁ intersect the x-axis at P
    ♦ L₂ intersect the x-axis at Q
• Thus we get a right angled triangle PQR
3. Formation of two angles:
• L₁ and L₂ intersect at R. The angle formed at R is marked as 𝜃.
• When 𝜃 is formed, another angle ɸ is also formed at the point of intersection.
• We see that: 𝜃 + ɸ = 180^o
4. Relation between 𝛼₁, 𝛼₂ and 𝜃:
• 𝛼₂ is an exterior angle of the triangle PQR
• For this exterior angle 𝛼₂, the angles 𝛼₁ and ∠PRQ are remote interior angles.
    ♦ ∠PRQ and 𝜃 are opposite angles
    ♦ So ∠PRQ = 𝜃
• Then we get: 𝛼₂ = 𝛼₁ + 𝜃
Which is same as: 𝜃 = 𝛼₂ - 𝛼₁
• This result can be used to find a relation between 𝜃, m₁ and m₂:

$\begin{array}{ll}
{}&{\theta}
&{}={}& {\alpha_2 - \alpha_1}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\tan (\alpha_2 - \alpha_1)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{\tan \alpha_2~-~\tan \alpha_1}{1~+~\tan \alpha_1 \tan \alpha_2}}
&{\color {green}{\text{- - - (a) }}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{m_2~-~m_1}{1~+~m_1 m_2}}
&{\color {green}{\text{- - - (b) }}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
(i) Line marked as (a):
See identity 11 in the list of identities.
(ii) Line marked as (b):
   ♦ tan 𝛼₁ is m₁
   ♦ tan 𝛼₂ is m₂


5. Using this relation, we can find 𝜃

---

Let us see an example:
Solved example 2
Two lines lying in the XY-plane have slopes $\frac{1}{2}$ and 3. Find the angle between them.
Solution:
1. Let m₁ = $\frac{1}{2}$ and m₂ = 3
• We are asked to find 𝜃
2. We have the equation: $\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\tan \theta}
&{}={}& {\frac{3~-~\frac{1}{2}}{1~+~\frac{1}{2}  × 3}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{6 ~-~1}{2~+~3}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{5}{5}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {1}
&{} \\

\end{array}$

3. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
2. Given that: tan 𝜃 = 1
• We know that 45^o is a principal solution.
• That means, we can put 45^o in place of 𝜃.
3. We will now find another principal solution.
• We have seen that, 𝜃 = 45^o is a principal solution.
• When the input 𝜃 is 45^o, the left side becomes tan 45^o
• This gives us: tan 𝜃 = tan 45^o = 1
• We want another angle such that, it's tangent is also 1
• Such an angle can be calculated using identities 9.f and 9.e [See the list of identities]: tan (π+x) = tan x
• We get:
tan 45^o = tan (180^o + 45^o) = tan 225^o
• So we can write:
tan 𝜃 = tan 45^o = tan 225^o
• Picking the first and last items, we get:
𝜃 = 225^o
   ♦ 225^o is greater than 0^o
   ♦ 225^o is less than 360^o  also.
   ♦ So it can be accepted as a principal solution.
• Thus we have two principal solutions for 𝜃:
𝜃 = 45^o and 𝜃 = 225^o
4. Fig.10.9 below shows how the two angles 45^o and 225^o are related to the given lines.

Fig.10.9

• The red line has a slope of $\frac{1}{2}$
Two convenient points points A and B are marked on this line.
• The green line has a slope of 3
Two convenient points points C and D are marked on this line.
• The two lines intersect at E
• ∠AEC (measured in the anti-clockwise direction) is the angle between the two lines. It's value is 45^o
• ∠BEC (measured in the anti-clockwise direction) is also an angle between the two lines. It's value is (180 + 45) = 225^o
5. In step (1), we took m₁ = $\frac{1}{2}$ and m₂ = 3.
• Since the order is not specified, we can take the reverse order also.
   ♦ That is., we interchange m₁ and m₂.
• Let us see if there is any change in the angles when we do the interchange. The following steps from (6) to (11) will give us the angles.
6. Let m₁ = 3 and m₂ = $\frac{1}{2}$
• We are asked to find 𝜃
7. We have the equation: $\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\tan \theta}
&{}={}& {\frac{\frac{1}{2}~-~3}{1~+~ 3 × \frac{1}{2}}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{1~-~6}{2~+~3}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {-\frac{5}{5}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {-1}
&{} \\

\end{array}$

8. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
9. Given that: tan 𝜃 = -1
• We know that 135^o is a principal solution.
• That means, we can put 135^o in place of 𝜃.
10. We will now find another principal solution.
• We have seen that, 𝜃 = 135^o is a principal solution.
• When the input 𝜃 is 135^o, the left side becomes tan 135^o
• This gives us: tan 𝜃 = tan 135^o = -1
• We want another angle such that, it's tangent is also -1
• Such an angle can be calculated using identities 9.f and 9.e: tan (π+x) = tan x
• We get:
tan 135^o = tan (180^o + 135^o) = tan 315^o
• So we can write:
tan 𝜃 = tan 135^o = tan 315^o
• Picking the first and last items, we get:
𝜃 = 315^o
   ♦ 315^o is greater than 0^o
   ♦ 315^o is less than 360^o  also.
   ♦ So it can be accepted as a principal solution.
• Thus we have two principal solutions for 𝜃:
𝜃 = 135^o and 𝜃 = 315^o
11. Fig.10.10 below shows how the two angles 135^o and 315^o are related to the given lines.

Fig.10.10

• The red line has a slope of $\frac{1}{2}$
Two convenient points points A and B are marked on this line.
• The green line has a slope of 3
Two convenient points points C and D are marked on this line.
• The two lines intersect at E
• ∠DEA (measured in the anti-clockwise direction) is the angle between the two lines. It's value is 135^o
• ∠DEB (measured in the anti-clockwise direction) is also an angle between the two lines. It's value is (∠DEA + ∠AEC + ∠CEB) = (135 + 45 +135) = 315^o
12. The figs.10.9 and 10.10 are exactly the same. They appear different because, in the first fig, we marked the acute angle between the given lines. In the second fig., we marked the obtuse angle. 
• Based on this, we can write a conclusion. It can be written in 3 steps:
(i) First we find tan 𝜃 using the equation:
$\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
(ii) If tan 𝜃 obtained is +ve, the 𝜃 so obtained is the acute angle between the given lines.
(iii) If tan 𝜃 obtained is -ve, the 𝜃 so obtained is the obtuse angle between the given lines.

---

Solved example 3
Two lines lying in the XY-plane have slopes $\frac{1}{2}$ and $-\frac{1}{3}$. Find the angle between them.
Solution:
1. Let m₁ = $\frac{1}{2}$ and m₂ = $-\frac{1}{3}$
• We are asked to find 𝜃
2. We have the equation: $\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\tan \theta}
&{}={}& {\frac{-\frac{1}{3}~-~\frac{1}{2}}{1~+~\frac{1}{2}  × -\frac{1}{3}}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{-2 ~-~3}{6~-~1}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{-5}{5}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {-1}
&{} \\

\end{array}$

3. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
2. Given that: tan 𝜃 = -1
• We know that 135^o is a principal solution.
• That means, we can put 135^o in place of 𝜃.
3. We will now find another principal solution.
• We have seen that, 𝜃 = 135^o is a principal solution.
• When the input 𝜃 is 135^o, the left side becomes tan 135^o
• This gives us: tan 𝜃 = tan 135^o = -1
• We want another angle such that, it's tangent is also -1
• Such an angle can be calculated using identities 9.f and 9.e [See the list of identities]: tan (π+x) = tan x
• We get:
tan 135^o = tan (180^o + 135^o) = tan 315^o
• So we can write:
tan 𝜃 = tan 135^o = tan 315^o
• Picking the first and last items, we get:
𝜃 = 315^o
   ♦ 315^o is greater than 0^o
   ♦ 315^o is less than 360^o  also.
   ♦ So it can be accepted as a principal solution.
• Thus we have two principal solutions for 𝜃:
𝜃 = 135^o and 𝜃 = 315^o
4. Fig.10.11 below shows how the two angles 135^o and 315^o are related to the given lines.

Fig.10.11

• The red line has a slope of $\frac{1}{2}$
Two convenient points points A and B are marked on this line.
• The green line has a slope of $-\frac{1}{3}$
Two convenient points points C and D are marked on this line.
• The two lines intersect at E
• ∠BEC (measured in the anti-clockwise direction) is the angle between the two lines. It's value is 135^o
• ∠BED (measured in the anti-clockwise direction) is also an angle between the two lines. It's value is (∠BEA + ∠AED) = (180 + 135) = 315^o
5. In step (1), we took m₁ = $\frac{1}{2}$ and m₂ = $-\frac{1}{3}$.
• Since the order is not specified, we can take the reverse order also.
• Since the order is not specified, we can take the reverse order also.
   ♦ That is., we interchange m₁ and m₂.
• Let us see if there is any change in the angles when order is reversed. The following steps from (6) to (11) will give us the angles.
6. Let m₁ = $-\frac{1}{3}$ and m₂ = $\frac{1}{2}$
• We are asked to find 𝜃
7. We have the equation: $\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
• Substituting the known values, we get:
$\begin{array}{ll}
{}&{\tan \theta}
&{}={}& {\frac{\frac{1}{2}~-~-\frac{1}{3}}{1~+~ -\frac{1}{3} × \frac{1}{2}}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{3~+~2}{6~-~1}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {\frac{5}{5}}
&{} \\

{\Rightarrow}&{\tan \theta}
&{}={}& {1}
&{} \\

\end{array}$

8. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
9. Given that: tan 𝜃 = 1
• We know that 45^o is a principal solution.
• That means, we can put 45^o in place of 𝜃.
10. We will now find another principal solution.
• We have seen that, 𝜃 = 45^o is a principal solution.
• When the input 𝜃 is 45^o, the left side becomes tan 45^o
• This gives us: tan 𝜃 = tan 45^o = 1
• We want another angle such that, it's tangent is also 1
• Such an angle can be calculated using identities 9.f and 9.e: tan (π+x) = tan x
• We get:
tan 45^o = tan (180^o + 45^o) = tan 225^o
• So we can write:
tan 𝜃 = tan 45^o = tan 225^o
• Picking the first and last items, we get:
𝜃 = 225^o
   ♦ 225^o is greater than 0^o
   ♦ 225^o is less than 360^o  also.
   ♦ So it can be accepted as a principal solution.
• Thus we have two principal solutions for 𝜃:
𝜃 = 45^o and 𝜃 = 225^o
11. Fig.10.12 below shows how the two angles 45^o and 225^o are related to the given lines.

Fig.10.12

• The red line has a slope of $\frac{1}{2}$
Two convenient points points A and B are marked on this line.
• The green line has a slope of $-\frac{1}{3}$
Two convenient points points C and D are marked on this line.
• The two lines intersect at E
• ∠CEA (measured in the anti-clockwise direction) is the angle between the two lines. It's value is 45^o
• ∠CEB (measured in the anti-clockwise direction) is also an angle between the two lines. It's value is (CEA + 180) = (45 +180) = 225^o
12. The figs.10.11 and 10.12 are exactly the same. They appear different because, in the first fig, we marked the obtuse angle between the given lines. In the second fig., we marked the acute angle. 
• Based on this, we can write the same conclusion that we wrote in the previous solved example. It can be written in 3 steps:
(i) First we find tan 𝜃 using the equation:
$\tan \theta~=~\frac{m_2~-~m_1}{1~+~m_1 m_2}$
(ii) If tan 𝜃 obtained is +ve, the 𝜃 so obtained is the acute angle between the given lines.
(iii) If tan 𝜃 obtained is -ve, the 𝜃 so obtained is the obtuse angle between the given lines.

---

In the next section, we will see a few more solved examples.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 10.1 - Slope of a Line

In the previous section, we saw some basic concepts and formulae in coordinate geometry. In this section, we will see slope of lines.

Inclination of a line and Slope of a line

First we will see inclination of a line. It can be written in 4 steps:
1. In fig.10.5(a) below,
(i) The angle between the line l₁ and the +ve side of the x-axis is 𝜃₁.
(ii) The angle 𝜃₁ is measured from the +ve side of the x-axis in the anti-clockwise direction.
• If the above two conditions are satisfied, then 𝜃₁ is called the inclination of the line l₁.

Fig.10.5

2. Consider the line l₂ in fig.10.5(b) above.
• Based on what we saw in fig.(a), we can write:
Inclination of the line l₂ is  𝜃₂
• This is because, the two conditions are satisfied:
(i) 𝜃₂ is measured from the +ve side of the x-axis.
(ii) 𝜃₂ is measured in the anti-clockwise direction.
3. Based on the two figs. (a) and (b), we can write:
• Inclination of a line parallel to the x-axis will be 0^o
• Inclination of a line parallel to the y-axis will be 90^o
4. So it is obvious that:
    ♦ Inclination of a line can never be less than 0^o.
    ♦ Inclination of a line can never be greater than 180^o.
• We can write: 0^o≤ 𝜃 ≤ 180^o.

---

Now we will see slope of a line. It can be written in steps:
1. We have seen how to write the inclination 𝜃 of any line l
• Now, tan 𝜃 is called the slope of that line l
2. Another name for slope is gradient.
• So we can write in either of the two ways:
    ♦ tan 𝜃 is the slope of the line l
    ♦ tan 𝜃 is the gradient of the line l
3. Slope of a line whose inclination is zero (a horizontal line) = tan 0 = 0
4. Slope of a line whose inclination is 90^o (a vertical line) = tan 90
    ♦ But tan 90 gives a number which does not exist.
    ♦ So slope of such a line is not defined
5. Based on this, we can write:
    ♦ Slope of x-axis = 0
    ♦ Slope of y-axis is not defined.

---

Slope from coordinates

• We know that, a line can be completely determined if we know the coordinates of any two points on it.
• If we know those coordinates, we can find the slope also. Let us see how it is done. It can be written in 7 steps:
1. In fig.10.6(a) below, the non-vertical line l has an inclination of 𝜃
• P (x₁, y₁) and Q (x₂,y₂) are two points on the line.

Fig.10.6

• Note:
In fig.10.6(a), x₁ cannot be equal to x₂. If they are equal, line l will become vertical. The slope of a vertical line is not defined.
2. A line QR is drawn perpendicular to the x-axis.
• Another line PM is drawn perpendicular to QR.
3. In the triangle PMQ, angle QPM will be equal to 𝜃.
So we can write:
$\text{Slope of}~l~=~\tan \theta ~=~\frac{QM}{PM}$
4. Now, the coordinates of M will be (x₂,y₁)
So the distance QM wil be (y₂ – y₁)
5. Since the coordinates of M are (x₂,y₁), the distance PM will be (x₂ – x₁)
6. Based on steps (3), (4) and (5), we get:
$\text{Slope of}~l~=~\tan \theta ~=~\frac{QM}{PM}~=~\frac{y_2 - y_1}{x_2 - x_1}$
7. Thus we get a simple method to find the slope using coordinates.

---

In the fig.10.6(a) above, the inclination 𝜃 is an acute angle. Let us see the case when 𝜃 is an obtuse angle. It can be written in steps:
1. In fig.10.6(b) above, the non-vertical line l has an inclination of 𝜃
• P (x₁, y₁) and Q (x₂,y₂) are two points on the line.
• Note:
In fig.10.6(b), x₁ cannot be equal to x₂. If they are equal, line l will become vertical. The slope of a vertical line is not defined.
2. A line QR is drawn perpendicular to the x-axis.
• Another line PM is drawn perpendicular to QR.
3. In the triangle PMQ, angle QPM will be equal to (180 - 𝜃).
So we can write:
$\text{Slope of}~l~=~\tan (180~-~\theta) ~=~-\tan \theta~=~\frac{QM}{PM}$
[See identities 9(c) and 9(d) in the list of identities]
4. Now, the coordinates of M will be (x₂,y₁)
So the distance QM wil be (y₂ – y₁)
5. Since the coordinates of M are (x₂,y₁), the distance PM will be (x₁ – x₂)
• Note that, in this case, we subtract x₂ from x₁ because, x₁ is larger than x₂.
6. Based on steps (3), (4) and (5), we get:
$\text{Slope of}~l~=~\tan (180~-~\theta) ~=~-\tan \theta~=~\frac{QM}{PM}~=~\frac{y_2 - y_1}{x_1 - x_2}$
• The -ve sign can be avoided by rearranging the denominator. We get:
$\text{Slope of}~l~=~\tan \theta~=~\frac{y_2 - y_1}{x_2 - x_1}$
7. Thus here also, we get the same simple method to find the slope using coordinates.

---

• If a line is horizontal, all points on that line will have the same y coordinates.
    ♦ That is., y₂ will be equal to y₁.
• Then the numerator will become zero.
• Consequently, tan 𝜃 will become zero.
• So the above result is applicable to all non-vertical lines, even if the line is horizontal.
• We can write:
If P (x₁, y₁) and Q (x₂,y₂) are two points on a non-vertical line, then the slope of that line will be equal to $\frac{y_2 - y_1}{x_2 - x_1}$
• Note that, in the numerator, we have a distance. Distance can be measured in meter or centimeter. In the denominator also, we have distance. So the units will cancel each other. That means: Slope has no units. It is just a number.

---

Condition for parallelism

This can be written in steps:
1. Fig.10.7(a) below shows two non-vertical lines l₁ and l₂.
    ♦ l₁ has an inclination of 𝛼
    ♦ l₂ has an inclination of β
    ♦ The slope of l₁ is m₁
    ♦ The slope of l₂ is m₂

Fig.10.7

2. From our earlier geometry classes, we know this:
    ♦ If l₁ and l₂ are parallel, then 𝛼 = β
3. But if 𝛼 = β, then tan 𝛼 = tan β
    ♦ If tan 𝛼 = tan β, then m₁ = m₂
• So the condition for two lines l₁ and l₂ to be parallel is:
Their slopes m₁ and m₂ must be equal.

---

Let us prove the converse.
• We need to prove that, if slopes m₁ and m₂ of the two lines l₁ and l₂ are equal, then the two lines are parallel.
It can be proved in 5 steps:
1. Given that, m₁ = m₂
Then we can write: tan 𝛼 = tan β
2. This is a trigonometrical equation. We have learned how to solve them in a previous chapter (see solved example 3.65 in section 3.17).
3. So, if tan 𝛼 = tan β, we can write:
𝛼 = n𝞹 + β
• Let us put the smallest possible value of 'n', which is 1
We get: 𝛼 = 𝞹 + β
4. But (𝞹 + β) is greater than 180^o
• Inclination cannot be greater than 180^o
• So the only possibility is that 𝛼 = β.
If 𝛼 = β, then the two lines are parallel
5. Thus we arrive at the conclusion:
If slopes m₁ and m₂ of two lines are equal, then the lines will be parallel.

---

Condition for perpendicularity

This can be written in 3 steps:
1. Fig.10.7(b) above shows two non-vertical lines l₁ and l₂.
    ♦ l₁ has an inclination of 𝛼
    ♦ l₂ has an inclination of β
    ♦ The slope of l₁ is m₁
    ♦ The slope of l₂ is m₂
2. Formation of triangle PQR:
    ♦ l₁ and l₂ intersect at R.
    ♦ l₁ intersect the x-axis at P
    ♦ l₂ intersect the x-axis at q
• Thus we get a right angled triangle PQR
3. Relation between 𝛼 and β:
• β is an exterior angle of the triangle PQR
• For this exterior angle β, the angles 𝛼 and 90^o are remote interior angles.
• So we get: β = 𝛼 + 90
• This result can be used to find a relation between the two slopes:

$\begin{array}{ll}
{}&{\beta}
&{}={}& {\alpha + 90^o}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \beta}
&{}={}& {\tan (\alpha + 90^o)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \beta}
&{}={}& {- \cot \alpha}
&{\color {green}{\text{- - - (a) }}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \beta}
&{}={}& {- \frac{1}{\tan \alpha}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{m_2}
&{}={}& {- \frac{1}{m_1}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{m_1 m_2}
&{}={}& {- 1}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
• Line marked as (a):
See identities 9(a) and 9(b) in the list of identities.
tan (90+𝜃) = -cot 𝜃
• So the condition for two lines l₁ and l₂ to be perpendicular is:
Product of their slopes (m₁ m₂) must be -1.

---

Let us prove the converse.
• We need to prove that, if product of the slopes (m₁ m₂) of the two lines l₁ and l₂ is -1, then the two lines are perpendicular to each other.
It can be proved in 3 steps:

1. Relation between 𝛼 and β:

$\begin{array}{ll}
{}&{m_1 m_2}
&{}={}& {-1}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \alpha × \tan \beta}
&{}={}& {-1}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \alpha}
&{}={}& {- \frac{1}{ \tan \beta}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \alpha}
&{}={}& {- \cot \beta}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\tan \alpha}
&{}={}& {\tan (90^o + \beta)}
&{\color {green}{\text{- - - (a) }}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\alpha}
&{}={}& {90^o + \beta}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
• Line marked as (a):
See identities 9(a) and 9(b) in the list of identities.
tan (90+𝜃) = -cot 𝜃

2. So 𝛼 and β differ by 90^o
• Then based on fig.10.7(b), the two lines will be perpendicular to each other.
3. So it is clear that, if (m₁m₂) = -1, then the two lines are perpendicular to each other.

Let us see a solved example

Solved example 10.1
Find the slope of the following lines:
(a) Line passing through the points (3,-2) and (-1,4)
(b) Line passing through the points (3,-2) and (7,-2)
(c) Line passing through the points (3,-2) and (3,4)
(d) Line making an inclination of 60^o with the positive direction of the x-axis.
Solution:
If a line pass through two points (x₁,y₁) and (x₂,y₂), then the slope of that line will be $\frac{y_2 - y_1}{x_2 - x_1}$ 
Part (a): Slope = $\frac{4 - -2}{-1 - 3}~=~\frac{6}{-4}~=~-\frac{3}{2}$
Part (b): Slope = $\frac{-2 - -2}{7 - 3}~=~\frac{0}{4}~=~0$
Part (c): Slope = $\frac{4 - -2}{3 - 3}~=~\frac{6}{0},~\text{which is not defined}$
Part (d): Slope is the tangent of inclination. So we get:
Slope = tan 60^o = $\sqrt{3}$

---

In the next section, we will see angle between two lines.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 10 - Straight Lines

In the previous section, we completed a discussion on sequences and series. In this chapter, we will see Straight lines.

In our earlier classes, we have discussed problems related to coordinate geometry. Let us recall some of those topics:

A. Significance of coordinates
This can be written in 3 steps:
1. In fig.10.1 below, points P and Q lie on the XY plane.

Fig.10.1

2. The coordinates of the point P are (4,1.5)
• Then we can write:
    ♦ P is at a distance of 4 units from the y-axis.
        ✰ This distance is measured along the +ve x-axis.
    ♦ P is at a distance of 1.5 units from the x-axis.
        ✰ This distance is measured along the +ve y-axis.
3. The coordinates of the point Q are (-2.5,-2)
• Then we can write:
    ♦ Q is at a distance of 2.5 units from the y-axis.
        ✰ This distance is measured along the -ve x-axis.
    ♦ Q is at a distance of 2 units from the x-axis.
        ✰ This distance is measured along the -ve y-axis

B. Distance between two points
This can be written in 3 steps:
1. In fig.10.2 below, points P (x₁,y₁) and Q (x₂,y₂) lie on the XY-plane.

Fig.10.2

2. Then the distance between the two points can be obtained using the formula:
$\rm{PQ~=~\sqrt{\left(x_2 - x_1 \right)^2~+~\left(y_2 - y_1 \right)^2}}$
3. For example, if (x₁,y₁) is (-2,2) and (x₂,y₂) is (3,-1), then:

$\begin{array}{ll}
{PQ}&{}={}
&{\sqrt{\left(3 - (-2) \right)^2~+~\left(-1 - 2 \right)^2}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\sqrt{\left(5 \right)^2~+~\left(-3 \right)^2}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\sqrt{25~+~9}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\sqrt{34}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{5.83~\text{units}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
\end{array}$

◼ We have seen this topic in our earlier classes (Details here) 

C. Division of a line in the ratio m:n
This can be written in 4 steps:
1. In fig.10.3 below, PQ is a line with end points P (x₁,y₁) and Q (x₂,y₂)

Fig.10.3

2. Point A divides the line in the ratio m:n
That is:
$\text{Distance PA = Distance PQ}~ × ~\frac{m}{m+n}$

$\text{Distance QA = Distance PQ}~ × ~\frac{n}{m+n}$
3. Then the coordinates of A are:
$\frac{m\, x_2 ~+~n\, x_1}{m+n},~\frac{m\, y_2 ~+~n\, y_1}{m+n}$       
◼ Note:
• For this formula to be valid,
    ♦ The "segment represented by the first component m", must be adjacent to the first point (x₁, y₁).
4. For example, let:
    ♦ P (x₁,y₁) be P (-2,2)
    ♦ Q (x₂,y₂) be Q (3,-1)
    ♦ Point A divides PQ in the ratio 3:10
• Then:
$\begin{array}{ll}
{\text{Coordinates of A}}&{}={}
&{\left(\frac{3 × 3~+~10 × -2}{3+10}\right.~,}& {\left. \frac{3 × -1~+~10 × 2}{3+10} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\left(\frac{9~-~20}{13}\right.~,}& {\left. \frac{-3~+~20}{13} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\left(\frac{-11}{13}\right.~,}& {\left. \frac{17}{13} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\left(-0.85 \right.~,}& {\left. 1.3 \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

• In this example, the ratio m:n is 3:10. The first component of the ratio is 3. The "segment represented by the first component 3", is adjacent to the first point P (-2,2).

◼ We have seen this topic in our earlier classes (Details here)

D. Division of a line in the ratio m:m
This can be written in 3 steps:
1. In this case, the point A divides the line PQ into two equal segments (remember that, m:m is same as 1:1).
• That means, A is the midpoint of PQ
2. We can write:
$\begin{array}{ll}
{\text{Coordinates of A}}&{}={}
&{\left(\frac{m\, x_2 ~+~n\, x_1}{m+n}\right.~,}& {\left. \frac{m\, y_2 ~+~n\, y_1}{m+n} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\left(\frac{m\, x_2 ~+~m\, x_1}{m+m}\right.~,}& {\left. \frac{m\, y_2 ~+~m\, y_1}{m+m} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\left(\frac{m(x_2 ~+~x_1)}{2m}\right.~,}& {\left. \frac{m(y_2 ~+~y_1}{2m} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\left(\frac{x_1 ~+~x_2}{2}\right.~,}& {\left. \frac{y_1 ~+~y_2}{2} \right)}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
\end{array}$

3. This result can be used as a formula:
Coordinates of the midpoint of the line PQ with P (x₁,y₁) and Q (x₂,y₂) are:
$\left(\frac{x_1~+~x_2}{2},\frac{y_1~+~y_2}{2} \right)$

E. Area of a Triangle
This can be written in 4 steps:
1. In fig.10.4 below, PQR is a triangle with vertices P (x₁,y₁), Q (x₂,y₂) and R (x₃,y₃)

Fig.10.4

2. Area of the triangle PQR will be equal to:
$\frac{1}{2}\left|x_1(y_2 - y_3)~+~x_2(y_3 - y_1)~+~x_3(y_1 - y_2) \right|$
• The calculations may give a -ve result. But we can ignore the -ve sign. This is indicated by the || lines.
3. Let us see an example:
If the vertices of a triangle are P (-1,5,2), Q (-2.5,-2) and R (4,1.5), then the area of that triangle will be:

$\begin{array}{ll}
{\text{Area}}&{}={}
&{\frac{1}{2}~ × ~\left |-1.5(-2 - 1.5)~+~-2.5(1.5 - 2)~+~4(2 - -2)\right |}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\frac{1}{2}~ × ~\left |-1.5(- 3.5)~+~-2.5(-0.5)~+~4(4)\right |}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\frac{1}{2}~ × ~\left |5.25~+~1.25~+~16\right |}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{\frac{1}{2}~ × ~\left |22.5\right |}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{}&{}={}
&{11.25~\text{square units}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\
\end{array}$

4. Suppose that we are given three points P, Q and R.
• Using their coordinates, we find the area formed by the three points.
• If that area works out to zero, we can confirm that, P, Q and R lie on a line.
    ♦ In other words, P, Q and R are collinear.

---

• We can draw geometric figures like triangles, rectangles, parallelograms etc., on the XY-plane. All we need is the "coordinates of the vertices" of those geometric figures.
• So it is clear that, coordinate geometry is a combination of coordinates and geometry.
• A line can be drawn between any two points on the XY-plane.
• A line can be defined by the coordinates of any two points on that line.
• By combining different lines, we can draw various geometric figures. So line is a basic concept in coordinate geometry.
• In the next section, we will see more details about lines.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 9.7 - Miscellaneous Examples on chapter 9

In the previous section, we completed a discussion on sequences and series. In this section, we will see some miscellaneous examples.

Solved example 9.21
If p^th, q^th, r^th and s^th terms of an A.P are in G.P, then show that (p-q), (q-r), (r-s) are also in G.P.
Solution:
1. We want to prove that (p-q), (q-r), (r-s) are in G.P.
• That means, we have to prove that $\frac{q-r}{p-q}~=~\frac{r-s}{q-r}$

2. Let 'a' be the first term and 'd' the common difference of the A.P.
• Then the given terms can be written as:
    ♦ p^th term = a_p = a + (p-1)d
    ♦ q^th term = a_q = a + (q-1)d
    ♦ r^th term = a_r = a + (r-1)d
    ♦ s^th term = a_s = a + (s-1)d
3. Given that, the above four terms are in G.P. So we can write:

$\begin{array}{ll}
{}&{\frac{a_q}{a_p}}
&{~=~\frac{a_r}{a_q}}& {~=~\frac{a_s}{a_r}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{a+(q-1)d}{a+(p-1)d}}
&{~=~\frac{a+(r-1)d}{a+(q-1)d}}& {~=~\frac{a+(s-1)d}{a+(r-1)d}}
&{\color {green} {\text{- - - - (a)}}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{a+(q-1)d~-~[a+(p-1)d]}{a+(p-1)d}}
&{~=~\frac{a+(r-1)d~-~[a+(q-1)d]}{a+(q-1)d}}& {~=~\frac{a+(s-1)d~-~[a+(r-1)d]}{a+(r-1)d}}
&{\color {green} {\text{- - - - (b)}}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{a+qd-d-a-pd+d}{a+(p-1)d}}
&{~=~\frac{a+rd-d-a-qd+d}{a+(q-1)d}}& {~=~\frac{a+sd-d-a-rd+d}{a+(r-1)d}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{(q-p)d}{a+(p-1)d}}
&{~=~\frac{(r-q)d}{a+(q-1)d}}& {~=~\frac{(s-r)d}{a+(r-1)d}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
(i) Line marked as (a):
This line is obtained by substituting the results from step (2)
(ii) Line marked as (b):
Here we apply componendo and dividendo rule:

$\begin{array}{ll}
{\text{If}}&{\frac{a}{b}~=~\frac{c}{d}}
&{\text{Then}}& {\frac{a-b}{b}~=~\frac{c-d}{d}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\text{Example:}}&{\frac{5}{2}~=~\frac{10}{4}}
&{\text{Then}}& {\frac{5-2}{2}~=~\frac{10-4}{4}~=~\frac{6}{4}~=~\frac{3}{2}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

4. Consider the above result in (3).
Take out the first two items. We get:

$\begin{array}{ll}
{}&{\frac{(q-p)d}{a+(p-1)d}}
&{~=~\frac{(r-q)d}{a+(q-1)d}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{p-q}{a+(p-1)d}}
&{~=~\frac{q-r}{a+(q-1)d}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{q-r}{p-q}}
&{~=~\frac{a+(q-1)d}{a+(p-1)d}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$ 

5. Consider again the result in (3).
Take out the last two items. We get:

$\begin{array}{ll}
{}&{\frac{(r-q)d}{a+(q-1)d}}
&{~=~\frac{(s-r)d}{a+(r-1)d}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{q-r}{a+(q-1)d}}
&{~=~\frac{r-s}{a+(r-1)d}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{r-s}{q-r}}
&{~=~\frac{a+(r-1)d}{a+(q-1)d}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

• From the line marked as (a) in step (3), we get:
$\frac{a+(r-1)d}{a+(q-1)d}~=~\frac{a+(q-1)d}{a+(p-1)d}$

• So we can write: $\frac{r-s}{q-r}~=~\frac{a+(q-1)d}{a+(p-1)d}$

6. Comparing the results in (4) and (5), we get:

$\frac{q-r}{p-q}~=~\frac{a+(q-1)d}{a+(p-1)d}~=~\frac{r-s}{q-r}$

• Hence the statement in (1) is proved.

Solved example 9.22
If a, b, c are in G.P and $a^{\frac{1}{x}}~=~b^{\frac{1}{y}}~=~c^{\frac{1}{z}}$, prove that x, y, z are in A.P.
Solution:
1. We want to prove that x, y, z are in A.P.
• That means, we have to prove that y - x = z - y
2. Given that $a^{\frac{1}{x}}~=~b^{\frac{1}{y}}~=~c^{\frac{1}{z}}$
Let us assume that, the three quantities are equal to k. So we can write:
$a^{\frac{1}{x}}~=~b^{\frac{1}{y}}~=~c^{\frac{1}{z}}~=~k$
3. Consider the above result in (2). Taking the first and last items, we get:

$\begin{array}{ll}
{}&{a^{\frac{1}{x}}}
&{~=~k}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\left(a^{\frac{1}{x}} \right)^x}
&{~=~k^x}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\left(a^{\frac{x}{x}} \right)}
&{~=~k^x}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\left(a^{1} \right)}
&{~=~k^x}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{a}
&{~=~k^x}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ In a similar way, we will get:
b = k^y and c = k^z

4. Now we get:
$\frac{b}{a}~=~\frac{k^y}{k^x}~=~k^{y-x}$
5. Also we get:
$\frac{c}{b}~=~\frac{k^z}{k^y}~=~k^{z-y}$
6. Given that a, b and c are in G.P. So we can write: $\frac{b}{a}~=~\frac{c}{b}$
7. So we can equate the results in (4) and (5). We get:
$\frac{b}{a}~=~\frac{c}{b}~=~k^{y-x}~=~k^{z-y}$
• Equating the powers of k, we get: y-x = z-y
• Hence the statement in (1) is proved.

Solved example 9.23
If a, b, c, d and p are different real numbers such that
$\left(a^2 + b^2 + c^2 \right)p^2~-~2(ab+bc+cd)p~+~\left(b^2 + c^2 + d^2 \right) ~\le~0$,
then show that a, b, c and d are in G.P.
Solution:
1. We want to prove that a, b, c and d are in G.P.
• That means, we have to prove that $\frac{b}{a}~=~\frac{c}{b}~=~\frac{d}{c}$.
2. The given inequality can be rearranged as follows:

$\begin{array}{ll}
{}&{\left(a^2 + b^2 + c^2 \right)p^2~-~2(ab+bc+cd)p~+~\left(b^2 + c^2 + d^2 \right)}
&{~\le~0}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\left(a^2 p^2 - 2abp + b^2 \right)~+~\left(b^2 p^2 - 2bcp + c^2 \right)~+~\left(c^2 p^2 - 2cdp + d^2 \right)}
&{~\le~0}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{(ap-b)^2~+~(bp-c)^2~+~(cp-d)^2}
&{~\ge~0}& {\color {green} {\text{- - - - (a)}}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
Line marked as (a):
• This line is a sum of three terms. Each of the three terms is a square.
    ♦ Given that: a, b, c, d and p are real numbers.
    ♦ So (ap-b), (bp-c) and (cp-d) will also be real numbers.
    ♦ Square of real numbers will be zero or +ve.
    ♦ So the sum of the three terms will be zero or +ve.
    ♦ Thus the sign in this line is changed to ≥.

3. The given inequality is only rearranged in the above step (2).
• The rearranged result in (2) is same as the given inequality.
• But the given inequality is ≤. In step (2), it changed to ≥.
• If both ≤ and ≥ are to be satisfied, the only possibility is that, both the expressions are equal to zero. 
4. So we can write: $(ap-b)^2~+~(bp-c)^2~+~(cp-d)^2~=~0$
• If the sum of certain squares is zero, each term in that sum must be zero.
• So we get:
(i) (ap-b)² = 0
(ii) (bp-c)² = 0
(iii) (cp-d)² = 0
5. If square of a real number is zero, then that real number must be zero.
So we get:
(i) ap-b = 0
(ii) bp-c = 0
(iii) cp-d = 0
• From 5(i), we get: $p=\frac{b}{a}$
• From 5(ii), we get: $p=\frac{c}{b}$
• From 5(iiii), we get: $p=\frac{d}{c}$
6. Based on the above step (5), we can write:
$\frac{b}{a}~=~\frac{c}{b}~=~\frac{d}{c}~=~p$
• Hence the statement in (1) is proved.

Solved example 9.24
If p, q, r are in G.P and the equations px² + 2qx + r = 0 and dx² + 2ex + f = 0 have a common root, then show that $\frac{d}{p}, \frac{e}{q}, \frac{f}{r}$ are in A.P.
Solution:
1. We want to prove that $\frac{d}{p}, \frac{e}{q}, \frac{f}{r}$ are in A.P.
• That means, we have to prove that:

$\begin{array}{ll}
{}&{\frac{e}{q} - \frac{d}{p}}
&{~=~\frac{f}{r} - \frac{e}{q}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{e}{q} + \frac{e}{q}}
&{~=~\frac{f}{r} + \frac{d}{p}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{2e}{q}}
&{~=~\frac{f}{r} + \frac{d}{p}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

2. Given that, p, q, r are in G.P. So we can write: q² = pr
3. Also given that, px² + 2qx + r = 0 and dx² + 2ex + f = 0 have a common root.
• Let us write the roots of the first equation. We get:

$\begin{array}{ll}
{}&{\frac{-2q \pm \sqrt{(2q)^2 ~-~4pr}}{2p}}
&{~=~\frac{-2q \pm \sqrt{4q^2 ~-~4pr}}{2p}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{~=~}&{\frac{-2q \pm \sqrt{4pr ~-~4pr}}{2p}}
&{~=~\frac{-2q \pm \sqrt{0}}{2p}}& {\color {green} {\text{- - - - (a)}}}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{~=~}&{\frac{-2q}{2p}}
&{~=~\frac{-q}{p}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
Line marked as (a): From (2), we have: q² = pr

4. So the first equation has only one root, which is: $\frac{-q}{p}$
• Given that, the two equations have a common root. So $\frac{-q}{p}$must be a root of the second equation also.
• Since $\frac{-q}{p}$ is a root of the second equation, we can write:

$\begin{array}{ll}
{}&{d \left(\frac{-q}{p} \right)^2~+~2e\left(\frac{-q}{p} \right)~+~f}
&{~=~0}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{d q^2}{p^2}~-~\frac{2eq}{p}~+~f}
&{~=~0}& {}
&{\color {green} {\text{- - - - (a)}}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{d q^2}{p^2 q^2}~-~\frac{2eq}{p q^2}~+~\frac{f}{q^2}}
&{~=~\frac{d}{p^2}~-~\frac{2e}{p q}~+~\frac{f}{q^2}}& {~=~0}
&{\color {green} {\text{- - - - (b)}}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{p d}{p^2}~-~\frac{2ep}{p q}~+~\frac{f p}{q^2}}
&{~=~\frac{d}{p}~-~\frac{2e}{q}~+~\frac{f p}{q^2}}& {~=~0}
&{\color {green} {\text{- - - - (c)}}}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{d}{p}~-~\frac{2e}{q}~+~\frac{f p}{pr}}
&{~=~\frac{d}{p}~-~\frac{2e}{q}~+~\frac{f}{r}}& {~=~0}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

{\Rightarrow}&{\frac{2e}{q}}
&{~=~\frac{d}{p}~+~\frac{f}{r}}& {}
&{}& {}
&{}& {}
&{}& {}&{}& {} &{} &{} &{} \\

\end{array}$

◼ Remarks:
(i) Line marked as (a):
We want to transform the statement in (a) to the staement in (1). For that, we divide by q²
(ii) Line marked as (b):
We want to further transform the statement in (b) to the statement in (1). For that, we multiply by p.
(iii) Line marked as (c):
From (2), we have: q² = pr
• Hence the statement in (1) is proved.

---

The link below gives some more solved examples

Miscellaneous Exercise on chapter 9

---

In the next chapter we will see straight lines.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com