In the previous section, we completed a discussion on solving linear inequalities in one variable. We saw some solved examples also. In this section, we will see linear inequalities in two variables.
• In the previous sections, we saw that graphical method is very effective to show all the acceptable values for linear inequalities in one variable. Graphical method is effective for two variables also. Some basics can be written in 5 steps:
1. In fig.6.7(a) below, the vertical red line divides the Cartesian plane into two parts.
• Each part is known as a half plane.
♦ Half plane on the left is known as the left half plane I.
♦ Half plane on the right is known as the right half plane II.
 |
| Fig.6.7 |
2. In fig.6.7(b) above, the red line is a sloping line. It slopes upwards as we move from left to right along the x axis. This sloping line divides the Cartesian plane into two parts. Here also, each part is known as a half plane.
♦ Half plane on the lower side is known as the lower half plane I.
♦ Half plane on the upper side is known as the upper half plane II.
3. In fig.6.7(c) above, the red line is a sloping line. It slopes downwards as we move from left to right along the x axis. This sloping line divides the Cartesian plane into two parts. Here also, each part is known as a half plane.
♦ Half plane on the lower side is known as the lower half plane I.
♦ Half plane on the upper side is known as the upper half plane II.
4. Consider the equation ax + by = c
• There will be a large number of ordered pairs (x,y) which will satisfy this equation.
• We know that ‘ordered pairs’ are points on the Cartesian plane.
♦ All points which satisfy the above equation will lie on a line.
♦ That line is the graph of the above equation.
5. So when we consider the infinite number of points in the Cartesian plane, there are three possibilities:
(i) A large number of those points will satisfy the equation ax + by = c
(ii) Another large number of points will satisfy the inequality ax + by < c
(iii) The remaining points will satisfy the inequality ax + by > c
◼ So now we can think about solving the inequalities:
• We want to be able to mark those points which satisfy the inequality ax + by < c.
♦ Those points will form the solution set of this inequality.
• We want to be able to mark those points also which satisfy the inequality ax + by > c.
♦ Those points will form the solution set of this inequality.
• The following 18 steps will help us to mark the required points.
1. Consider the equation ax + by = c
• We know that, the general form of a line is: y = mx +c
• We can transform ax + by = c into the general form:
$\begin{array}{ll}
{}&ax+by &{}={}& {c} &{} \\
\Rightarrow &ax+by-ax&{}={}& c-ax &{} \\
\Rightarrow &by&{}={}& -ax+c &{} \\
\Rightarrow &\frac{by}{b}&{}={}& \frac{-ax+c}{b} &{} \\
\Rightarrow &y&{}={}& {\frac{-a}{b}}x+\frac{c}{b} &{} \\
\Rightarrow &y&{}={}& {\frac{-a}{b}}x+c &{} \\
{} &{}&{}& \color {green}{\frac{c}{b}~\text{is a constant. So it can be denoted by 'c'}}&{} \\
\Rightarrow &y&{}={}& -mx+c &{} \\
{} &{}&{}& \color {green}{\frac{a}{b}~\text{is a constant. So it can be denoted by 'm'}}&{} \\
\end{array}$
2. Consider the equation ax - by = c
• We know that, the general form of a line is: y = mx +c
• We can transform ax - by = c into the general form:
$\begin{array}{ll}
{}&ax-by &{}={}& {c} &{} \\
\Rightarrow &ax-by-ax&{}={}& c-ax &{} \\
\Rightarrow &-by&{}={}& -ax+c &{} \\
\Rightarrow &\frac{-by}{-b}&{}={}& \frac{ax+c}{-b} &{} \\
\Rightarrow &y&{}={}& {\frac{-a}{-b}}x + \frac{c}{-b}&{} \\
\Rightarrow &y&{}={}& {\frac{a}{b}}x - \frac{c}{b}&{} \\
\Rightarrow &y&{}={}& {\frac{a}{b}}x-c &{} \\
{} &{}&{}& \color {green}{\frac{c}{b}~\text{is a constant. So it can be denoted by 'c'}}&{} \\
\Rightarrow &y&{}={}& mx-c &{} \\
{} &{}&{}& \color {green}{\frac{a}{b}~\text{is a constant. So it can be denoted by 'm'}}&{} \\
\end{array}$
3. We can write:
♦ ax + by = c in general form is: y = -mx - c
♦ ax - by = c in general form is: y = mx + c
• We see that, the sign of b will determine the sign of m.
• From our earlier classes, we know that:
♦ If m is +ve, the line will slope upwards.
♦ If m is -ve, the line will slope downwards. (Details here)
• Thus we get:
♦ If b is +ve, the line will slope downwards.
♦ If b is -ve, the line will slope upwards.
• What about the signs of a and c?
The answer can be written in 2 steps:
(i) The sign of 'a' can be always made +ve. This is by multiplying the whole equation by -1 if necessary.
(ii) The sign of 'c' can be +ve or -ve. It will not affect the slope of the line.
• Now we have a good knowledge about the shape of the line. We can proceed to investigate inequalities.
• The steps from (4) to (9) will help us to understand the inequality when b is +ve. That is, b > 0
• The steps from (10) to (16) will help us to understand the inequality when b is -ve. That is, b < 0
4. Consider the equation ax + by = c
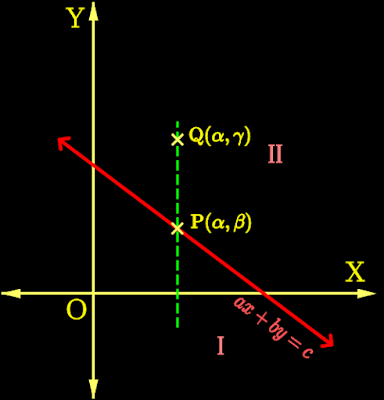
• Since 'b' is +ve, the line will slope downwards. This is shown in fig.6.8 below:
 |
| Fig.6.8 |
• Let P(𝛼,β) be a point on the line. Then both 𝛼 and β will satisfy the equation ax+by = c
We can write: a𝛼 + bβ = c
5. Now consider a point Q in such a way that:
♦ Q lies in the vertical line through P
♦ Q is in the half plane II
• Since Q and P are in the same vertical line, both of them will have the same x coordinate .
♦ Let the y coordinate be 𝛾
♦ Then the coordinates of Q will be (𝛼,𝛾)
6. Since Q is in the half plane II, it is at a higher level than P.
♦ So the y coordinate of Q
♦ will be greater than
♦ the y coordinate of P
• We can write: 𝛾 > β
♦ Multiplying both sides by b, we get: b𝛾 > bβ (Rule 2)
♦ Adding a𝛼 on both sides we get: a𝛼+b𝛾 > a𝛼+bβ (Rule 1)
7. But from step (4), we have: a𝛼+bβ = c
• So the result in (6) becomes: a𝛼+b𝛾 > c
• That means:
The point Q(𝛼,𝛾) will satisfy the inequality ax + by > c
• Q(𝛼,𝛾) is a general point that we took in half plane II
• So we can write:
All points that lie in the half plane II will satisfy the inequality ax + by > c, where b >0
8. Now we have to prove the converse:
If a point Q(𝛼,𝛾) satisfies the inequality ax+by > c, where b>0, then Q(𝛼,𝛾) will be on the half plane II.
This can be done in 4 steps:
(i) Given that: Q(𝛼,𝛾) satisfies the inequality ax+by >c
Then we can write: a𝛼 + b𝛾 > c
(ii) But from step (4), we have: a𝛼+bβ = c
• So the result in (i) becomes: a𝛼+b𝛾 > a𝛼+bβ
• Subtracting a𝛼 from both sides, we get:
b𝛾 > bβ (Rule 1)
(iii) Dividing both sides by b, we get: 𝛾 > β (Rule 2)
• The sign will not reverse because b is greater than zero.
(iv) Since P and Q are on the same vertical line, 𝛾 > β implies that Q lies in the half plane II.
9. So when b > 0, we have the details about all three regions:
(i) The region which lies exactly on the line ax+by=c,
♦ will contain all those points
♦ which satisfy the equation ax+by=c
(ii) The region of half plane II,
♦ will contain all those points
♦ which satisfy the inequality ax+by > c
(iii) Obviously the remaining region of half plane I,
♦ will contain all those points
♦ which satisfy the inequality ax+by < c
10. Now we can investigate the case when b < 0
• Consider the equation ax + by = c
• Since 'b' is -ve, the line will slope upwards. This is shown in fig.6.9 below:
 |
| Fig.6.9 |
• Let P(𝛼,β) be a point on the line. Then both 𝛼 and β will satisfy the equation ax+by = c
We can write: a𝛼 + bβ = c
11. Now consider a point Q in such a way that:
♦ Q lies in the vertical line through P
♦ Q is in the half plane II
• Since Q and P are in the same vertical line, both of them will have the same x coordinate .
♦ Let the y coordinate be 𝛾
♦ Then the coordinates of Q will be (𝛼,𝛾)
12. Since Q is in the half plane II, it is at a higher level than P.
♦ So the y coordinate of Q
♦ will be greater than
♦ the y coordinate of P
• We can write: 𝛾 > β
♦ Multiplying both sides by b, we get: b𝛾 < bβ (Rule 3)
• The sign will reverse because b is less than zero.
♦ Adding a𝛼 on both sides we get: a𝛼+b𝛾 < a𝛼+bβ (Rule 1)
13. But from step (4), we have: a𝛼+bβ = c
• So the result in (12) becomes: a𝛼+b𝛾 < c
• That means:
The point Q(𝛼,𝛾) will satisfy the inequality ax + by < c
• Q(𝛼,𝛾) is a general point that we took in half plane II
• So we can write:
All points that lie in the half plane II will satisfy the inequality ax + by < c, where b < 0
14. Now we have to prove the converse:
If a point Q(𝛼,𝛾) satisfies the inequality ax+by < c, where b<0, then Q(𝛼,𝛾) will be on the half plane II.
• This can be done in 4 steps:
(i) Given that: Q(𝛼,𝛾) satisfies the inequality ax+by < c
Then we can write: a𝛼 + b𝛾 < c
(ii) But from step (4), we have: a𝛼+bβ = c
• So the result in (i) becomes: a𝛼+b𝛾 < a𝛼+bβ
• Subtracting a𝛼 from both sides, we get:
b𝛾 < bβ (Rule 1)
(iii) Dividing both sides by b, we get: 𝛾 > β (Rule 3)
• The sign will reverse because b is less than zero.
(iv) Since P and Q are on the same vertical line, 𝛾 > β implies that Q lies in the half plane II.
15. So when b < 0, we have the details about all three regions:
(i) The region which lies exactly on the line ax+by=c,
♦ will contain all those points
♦ which satisfy the equation ax+by=c
(ii) The region of half plane II,
♦ will contain all those points
♦ which satisfy the inequality ax+by < c
(iii) Obviously the remaining region of half plane I,
♦ will contain all those points
♦ which satisfy the inequality ax+by > c
16. Based on the results in steps (9) and (15), we can prepare a table:
 |
| Table 6.1 |
• Let us see a sample application of this table. We will consider the same inequality that we saw at the beginning of this chapter.
Example 4: 20x + 8y ≤ 120
It can be written in 4 steps:
(i) Suppose we want to solve the inequality 20x+8y < 120
• Let us first compare it with the standard form: ax +by < c
♦ We see that, b is +ve. And the sign before c is '<'
♦ So from the table, we get: Lower plane I
(ii) In fig.6.10 below, the red line is the graph of 20x + 8y = 120
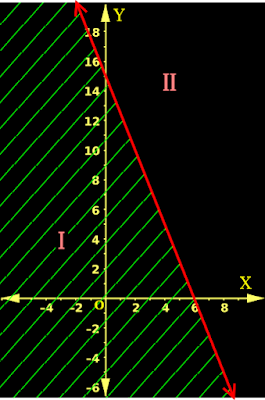 |
| Fig.6.10 |
• This line divides the Cartesian plane into Lower half plane I and upper half plane II
• All points in the lower half plane I will satisfy the inequality 20x+8y < 120
• We can check this using any convenient point. O(0,0) is convenient for calculations. So we will use that point.
• If we input (0,0) in the inequality, we will get:
♦ (20 × 0) + (8 × 0) < 120
♦ ⇒ 0 + 0 < 120
♦ ⇒ 0 < 120, which is true.
(iii) O(0,0) lies in the lower half plane I. The check confirms that, all points in the lower half plane I will satisfy the inequality 20x+8y < 120
• So we hatch the entire lower half plane I using green lines.
• The area hatched using green lines is the graph of the inequality 20x+8y < 120
• Note that:
♦ Graph of an "inequality in one variable" is a line.
♦ Graph of an "inequality in two variables" is not a line, but an area.
(iv) On a sheet of paper or on the computer screen, we can hatch only a limited area.
◼ But the actual hatched area extends up to infinity.
• The red line goes upwards up to (-∞,∞)
♦ So the left boundary of the hatched area is -∞
♦ Also the top boundary of the hatched area is ∞
• The red line goes downwards up to (∞,-∞)
♦ So the right boundary of the hatched area is ∞
♦ Also the bottom boundary of the hatched area is -∞
(v) Now let us consider the fact that the sign of our present inequality is '≤' not '<'. For simplicity we ignored '≤' in step (i)
• Since the sign to be considered is '≤', the points on the red line representing 20x + 8y = 120 are also acceptable.
• So we draw the line of the equation using a bold red line.
• If the sign is '<', we would draw the line of the equation using a dashed red line.
◼ The rule is:
♦ Bold line for '≤' and '≥'
♦ Dashed line for '<' and '>'
17. So now we have a basic idea about how to draw the graph of an inequality.
• In the above step (16), we saw that,
♦ all points in the hatched area
♦ and all point in the red line
♦ are solutions of the inequality 20x+8y ≤ 120
For example, (-√2,1) is a point in the hatched area.
• If we input (-√2,1) in the inequality, we will get:
♦ (20 × -√2) + (8 × 1) < 120
♦ ⇒ (20 × -1.414) + (8 × 1) < 120
♦ ⇒ -28.284 + 8 < -20.284, which is true
• For our particular problem, we need to make an adjustment. It can be written in 5 steps:
(i) For our particular problem, x and y are to be whole numbers. Because they represent the numbers of books and pens that are purchased.
(ii) So we have to:
♦ pick out those points from the hatched area
♦ in such a way that,
♦ both x and y coordinates of those points are whole numbers.
• Such points are shown as magenta dots in fig.6.11 below:
 |
| Fig.6.11 |
(iii) All points in the graph of 20x+8y = 120 are not formed by x and y whole numbers. So we cannot draw it as a bold line. We must draw it as a dashed line.
(iv) All magenta dots in fig.6.11 will satisfy the inequality 20x+8y ≤ 120
For example, consider (3,6)
• If we input (0,0) in the inequality, we will get:
♦ (20 × 3) + (8 × 6) ≤ 120
♦ ⇒ 60 + 24 ≤ 120
♦ ⇒ 84 ≤ 120, which is true.
(v) Only five points on the dashed red line satisfy the inequality.
They are: (6,0), (4,5), (2,10) and (0,15)
18. Based on the above step (17), we can write:
• If x and y are real numbers, graph of the inequality can be drawn by hatching the entire area of the appropriate half plane.
• If x and y are integers or whole numbers, graph of the inequality can be drawn by putting dots at the appropriate points.
• In the next section, we will see a few more examples.
Copyright©2022 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment