In the previous section, we saw Cartesian product. In this section, we will see relations.
We will see the basics about relations using three examples.
Example 1:
This can be written in 7 steps:
1. Consider two sets A and B
♦ A is a set of four students: Student 1, Student 2, Student 3, Student 4.
✰ A = {1, 2, 3, 4}
♦ B is a set of five available courses.
✰ B = {Maths, Physics, Chemistry, Biology, Geography}
2. The students have the liberty to learn one or more of the available courses.
• So there are twenty possible combinations. They are:
(1, Maths), (2, Maths), (3, Maths), (4, Maths),
(1, Physics), (2, Physics), (3, Physics), (4, Physics),
(1, Chemistry), (2, Chemistry), (3, Chemistry), (4, Chemistry),
(1, Biology), (2, Biology), (3, Biology), (4, Biology),
(1, Geography), (2, Geography), (3, Geography), (4, Geography).
• They are the 20 ordered pairs.
3.
Using the method that we saw in the previous section, the above twenty
ordered pairs can be denoted by red dots. This is shown in fig.2.4(a)
below:
 |
| Fig.2.4 |
• So the red dots are useful during the admission processes. They help students and authorities to select and allocate various courses.
• Once the admission processes are complete, the red dots have not much value. At that stage, we will be wanting to know which student chose which course.
5. So we need to pick the appropriate red dots from among the total 20 red dots. This is shown in fig.2.4(b) above. The selected dots are marked with green circles.
• Consider any one green circle. Say the one at the intersection of student 2 line and Chemistry line.
• This green circle indicates that, student 2 chose to do the chemistry course.
6. The ordered pairs with green circle are:
(1, Maths), (2, Maths), (2, Chemistry), (3, Chemistry), (3, Biology), and (4, Geography)
• These pairs give us the following information:
♦ Student 1 chose to do Maths.
♦ Student 2 chose to do Maths.
♦ Student 2 chose to do Chemistry.
♦ Student 3 chose to do Chemistry.
♦ Student 3 chose to do Biology.
♦ Student 4 chose to do Geography.
7. This information can be shown in an arrow diagram also. It is shown in fig.2.4(c) above.
• Note that:
♦ The number of green circles in fig.b is 6
♦ The number of green arrows in fig.c is also 6
• This is because, both the figs. b and c convey the same information.
• Let us write this example in terms of sets and ordered pairs. The 8 steps given below will help us:
1. A is the set of students and B is the set of courses.
2. All the ‘possible combinations’ is given by the red dots in fig.2.4(a)
• As we saw in the previous section, all those red dots will be included in the set A × B
3. The green circles in fig.2.4(b) shows the relation between students and their chosen courses.
• We can make a set R which contains all the green circles in fig.2.4(b)
4. All the green circles are obtained from the red dots. So the set R will be a subset of A × B
• We can write: R ⊂ (A × B)
5. In the previous section, we saw that all elements of A × B are ordered pairs.
• Since R is a subset of A × B, all the elements of R will also be ordered pairs.
• In our present case,
R = {(1, Maths), (2, Maths), (2, Chemistry), (3, Chemistry), (3, Biology), and (4, Geography)}
6. The green circles in fig.b can be better visualized using the arrow diagram in fig.c
♦ The green circles in fig.b give us the ordered pairs in R.
♦ The green arrows in fig.c give us the same ordered pairs in R.
7. The usefulness of the arrow diagram will be clear from the following 3 steps:
(i) Take any ordered pair in R. Look at the corresponding green arrow in the arrow diagram.
(ii) The tail end of the arrow will be the first element of that ordered pair.
(iii) The head end of the arrow will be the second element of that ordered pair.
• We can work in the reverse also. It can be written in 4 steps:
(i) Take any green arrow in the arrow diagram. Corresponding to that arrow, there will be an ordered pair in R.
(ii) The tail end of the arrow will be the first element of that ordered pair.
(iii) The head end of the arrow will be the second element of that ordered pair.
(iv) All the green arrows must be included as ordered pairs in the set R.
8.
In step (5), we wrote R in the roster form. We must be able to write it
in the set builder form also. The following 3 steps will enable us to
do so:
(i) We know that, set R contains ordered pairs. Let the general form of those ordered pairs be (x,y)
(ii) Then x will be the student and y will be the course chosen by that student.
(iii) So the set builder form will be:
R = {(x,y) : y is the course chosen by student x, x ∈ A, y ∈ B}
Example 2:
This can be written in 6 steps:
1. Consider two sets A and B
♦ A = {5, 6, 7}
♦ B = {3, 4, 5}
2. n(A) = 3 and n(B) = 3
• So there are nine possible combinations. They are:
(5, 3), (6, 3), (7, 3),
(5, 4), (6, 4), (7, 4),
(5, 5), (6, 5), (7, 5).
• They are the 9 ordered pairs.
3.
Using the method that we saw in the previous section, the above nine
ordered pairs can be denoted by red dots. This is shown in fig.2.5(a)
below:
 |
| Fig.2.5 |
Suppose that, we want only those combinations in which:
♦ The element taken from B
♦ is 2 less than
♦ The element taken from A.
• Then we need to pick the appropriate red dots from among the total 9 red dots.
• The appropriate red dots can be determined using 2 steps:
(i) Let x be the element (which satisfies the relation) from A. Let y be the corresponding element (which satisfies the relation) from B
• Then the algebraic form of the relation is: x - 2 = y
(ii) Let us take each possible value for x from set A:
• When x = 5,
♦ y = (x-2) = (5-2) = 3
♦ '3' is available in B
♦ So the ordered pair (5, 3) satisfies the given relation.
✰ Note that (5, 3) is one among the red dots in fig.a
• When x = 6,
♦ y = (x-2) = (6-2) = 4
♦ '4' is available in B
♦ So the ordered pair (6, 4) satisfies the given relation.
✰ Note that (6, 4) is one among the red dots in fig.a
• When x = 7,
♦ y = (x-2) = (7-2) = 5
♦ '5' is available in B
♦ So the ordered pair (7, 5) satisfies the given relation.
✰ Note that (7, 5) is one among the red dots in fig.a
5. We need to select the above three ordered pairs from among the 9 ordered pairs. This is shown in fig.2.5(b) above. The selected dots are marked with green circles.
• The ordered pairs with green circle are:
(5, 3), (6, 4) and (7, 5)
6. This information can be shown in an arrow diagram also. It is shown in fig.2.5(c) above.
• Note that:
♦ The number of green circles in fig.b is 3
♦ The number of green arrows in fig.c is also 3
• This is because, both the figs. b and c convey the same information.
• Let us write this example in terms of sets and ordered pairs. The 8 steps given below will help us:
1. A = {5, 6, 7} and B = {3, 4, 5}
2. All the ‘possible combinations’ is given by the red dots in fig.2.5(a)
• As we saw in the previous section, all those red dots will be included in the set A × B
3. The green circles in fig.2.5(b) shows those ordered pairs which satisfy a particular relation.
• The relation is this:
♦ The element taken from B
♦ is 2 less than
♦ The element taken from A.
• We can make a set R which contains all the green circles in fig.2.4(b)
4. All the green circles are obtained from the red dots. So the set R will be a subset of A × B
• We can write: R ⊂ (A × B)
5. In the previous section, we saw that all elements of A × B are ordered pairs.
• Since R is a subset of A × B, all the elements of R will also be ordered pairs.
• In our present case,
R = {(5, 3), (6, 4), (7, 5)}
6. The green circles in fig.b can be better visualized using the arrow diagram in fig.c
♦ The green circles in fig.b give us the ordered pairs in R.
♦ The green arrows in fig.c give us the same ordered pairs in R.
7. The usefulness of the arrow diagram will be clear from the following 3 steps:
(i) Take any ordered pair in R. Look at the corresponding green arrow in the arrow diagram.
(ii) The tail end of the arrow will be the first element of that ordered pair.
(iii) The head end of the arrow will be the second element of that ordered pair.
• We can work in the reverse also. It can be written in 4 steps:
(i) Take any green arrow in the arrow diagram. Corresponding to that arrow, there will be an ordered pair in R.
(ii) The tail end of the arrow will be the first element of that ordered pair.
(iii) The head end of the arrow will be the second element of that ordered pair.
(iv) All the green arrows must be included as ordered pairs in the set R.
8.
In step (5), we wrote R in the roster form. We must be able to write it
in the set builder form also. The following 3 steps will enable us to do
so:
(i) We know that, set R contains ordered pairs. Let the general form of those ordered pairs be (x,y)
(ii) Then x will be the element from A and y will be the element from B.
(iii) So the set builder form will be:
R = {(x,y) : y = x - 2, x ∈ A, y ∈ B}
Example 3:
This can be written in 6 steps:
1. Consider the set A
♦ A = {1, 2, 3, 4, 5, 6}
2. We want the possible combinations of A with itself.
n(A) = 6
• So there are 36 possible combinations. They are:
(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1),
(1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2),
(1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3),
(1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4),
(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5),
(1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 6).
• They are the 36 ordered pairs.
3.
Using the method that we saw in the previous section, the above 36
ordered pairs can be denoted by red dots. This is shown in fig.2.6(a)
below:
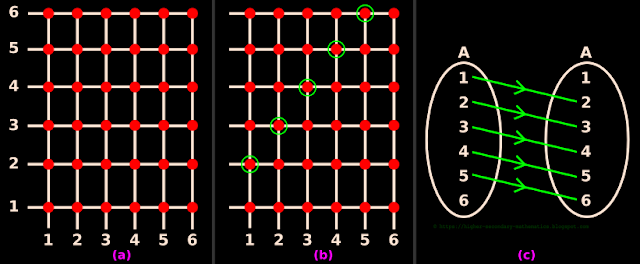 |
| Fig.2.6 |
Suppose that, we want only those combinations in which:
♦ The element taken from B
♦ is 1 greater than
♦ The element taken from A.
• Then we need to pick the appropriate red dots from among the total 36 red dots.
• The appropriate red dots can be determined using 2 steps:
(i) Let x be the element (which satisfies the relation) from A. Let y be the corresponding element (which satisfies the relation) from B
• Then the algebraic form of the relation is: x + 1 = y
(ii) Let us take each possible value for x from set A:
• When x = 1,
♦ y = (x+1) = (1+1) = 2
♦ '2' is available in A
♦ So the ordered pair (1, 2) satisfies the given relation.
✰ Note that (1, 2) is one among the red dots in fig.a
• When x = 2,
♦ y = (x+1) = (2+1) = 3
♦ '3' is available in A
♦ So the ordered pair (2, 3) satisfies the given relation.
✰ Note that (2, 3) is one among the red dots in fig.a
• When x = 3,
♦ y = (x+1) = (3+1) = 4
♦ '4' is available in A
♦ So the ordered pair (3, 4) satisfies the given relation.
✰ Note that (3, 4) is one among the red dots in fig.a
• When x = 4,
♦ y = (x+1) = (4+1) = 5
♦ '5' is available in A
♦ So the ordered pair (4, 5) satisfies the given relation.
✰ Note that (4, 5) is one among the red dots in fig.a
• When x = 5,
♦ y = (x+1) = (5+1) = 6
♦ '6' is available in A
♦ So the ordered pair (5, 6) satisfies the given relation.
✰ Note that (5, 6) is one among the red dots in fig.a
• When x = 6,
♦ y = (x+1) = (6+1) = 7
♦ '7' is not available in A
♦ So the ordered pair (6, 7) does not satisfy the given relation.
✰ Note that (6, 7) is not among the red dots in fig.a
5. We need to select the above five ordered pairs from among the 36 ordered pairs. This is shown in fig.2.6(b) above. The selected dots are marked with green circles.
• The ordered pairs with green circle are:
(1, 2), (2, 3), (3, 4), (4, 5) and (5, 6)
6. This information can be shown in an arrow diagram also. It is shown in fig.2.6(c) above.
• Note that:
♦ The number of green circles in fig.c is 5
♦ The number of green arrows in fig.c is also 5
• This is because, both the figs. b and c convey the same information.
• Let us write this example in terms of sets and ordered pairs. The 8 steps given below will help us:
1. A = {1, 2, 3, 4, 5, 6}
2. All the ‘possible combinations’ from A to A is given by the red dots in fig.2.6(a)
• As we saw in the previous section, all those red dots will be included in the set A × A
3. The green circles in fig.2.6(b) shows those ordered pairs which satisfy a particular relation.
• The relation is this:
♦ The element taken from A
♦ is 1 greater than
♦ The element taken from A.
• We can make a set R which contains all the green circles in fig.2.6(b)
4. All the green circles are obtained from the red dots. So the set R will be a subset of A × A
• We can write: R ⊂ (A × A)
5. In the previous section, we saw that all elements of A × A are ordered pairs.
• Since R is a subset of A × A, all the elements of R will also be ordered pairs.
• In our present case,
R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}
6. The green circles in fig.b can be better visualized using the arrow diagram in fig.c
♦ The green circles in fig.b give us the ordered pairs in R.
♦ The green arrows in fig.c give us the same ordered pairs in R.
7. The usefulness of the arrow diagram will be clear from the following 3 steps:
(i) Take any ordered pair in R. Look at the corresponding green arrow in the arrow diagram.
(ii) The tail end of the arrow will be the first element of that ordered pair.
(iii) The head end of the arrow will be the second element of that ordered pair.
• We can work in the reverse also. It can be written in 4 steps:
(i) Take any green arrow in the arrow diagram. Corresponding to that arrow, there will be an ordered pair in R.
(ii) The tail end of the arrow will be the first element of that ordered pair.
(iii) The head end of the arrow will be the second element of that ordered pair.
(iv) All the green arrows must be included as ordered pairs in the set R.
8.
In step (5), we wrote R in the roster form. We must be able to write it
in the set builder form also. The following steps will enable us to do
so:
(i) We know that, set R contains ordered pairs. Let the general form of those ordered pairs be (x,y)
(ii) Then x will be the element from A and y will be the element from A.
(iii) So the set builder form will be:
R = {(x,y) : y = x + 1, x ∈ A, y ∈ A}
• The above three examples help us to understand the basics about relations.
• We will now see some important terms involved with relations. The important terms are:
(a) image
(b) domain
(c) range
(d) Codomain
(a) image:
This can be explained in 3 steps:
1. We know that, the set R will contain one or more ordered pairs.
2. Each of those ordered pairs will have two elements.
3. The second element is called the image of the first element.
◼ Consider the ordered pairs in R of our first example. We can write:
♦ Maths is the image of student 1
♦ Maths is the image of student 2
♦ Chemistry is the image of student 2
♦ Chemistry is the image of student 3
♦ Biology is the image of student 3
♦ Geography is the image of student 4
◼ Consider the ordered pairs in R of our second example. We can write:
♦ 3 is the image of 5
♦ 4 is the image of 6
♦ 5 is the image of 7
◼ Consider the ordered pairs in R of our third example. We can write:
♦ 2 is the image of 1
♦ 3 is the image of 2
♦ 4 is the image of 3
♦ 5 is the image of 4
♦ 6 is the image of 5
(b) domain:
This can be explained in 5 steps:
1. We know that, the set R will contain one or more ordered pairs.
2. Each of those ordered pairs will have two elements.
3. Pick out all the first elements.
4. Make a set using those first elements.
5. This set is called the domain of the relation R.
◼ Consider the ordered pairs in R of our first example. We can write:
♦ The first elements are: 1, 2, 2, 3, 3, 4
♦ When we write them as a set, repeating elements should appear only once.
♦ So we get: domain = {1, 2, 3, 4}
◼ Consider the ordered pairs in R of our second example. We can write:
♦ The first elements are: 5, 6, 7
♦ Here there are no repeating elements.
♦ So we get: domain = {5, 6, 7}
◼ Consider the ordered pairs in R of our third example. We can write:
♦ The first elements are: 1, 2, 3, 4, 5
♦ Here there are no repeating elements.
♦ So we get: domain = {1, 2, 3, 4, 5}
(c) range:
This can be explained in 5 steps:
1. We know that, the set R will contain one or more ordered pairs.
2. Each of those ordered pairs will have two elements.
3. Pick out all the second elements.
4. Make a set using those second elements.
5. This set is called the range of the relation R.
◼ Consider the ordered pairs in R of our first example. We can write:
♦ The second elements are: maths, maths, chemistry, chemistry, biology, geography.
♦ When we write them as a set, repeating elements should appear only once.
♦ So we get: range = {maths, chemistry, biology, geography}
◼ Consider the ordered pairs in R of our second example. We can write:
♦ The second elements are: 3, 4, 5
♦ Here there are no repeating elements.
♦ So we get: range = {3, 4, 5}
◼ Consider the ordered pairs in R of our third example. We can write:
♦ The second elements are: 2, 3, 4, 5, 6
♦ Here there are no repeating elements.
♦ So we get: domain = {2, 3, 4, 5, 6}
(d) codomain:
We know that, the relation R is defined from set A to set B.
• The set B is also known as codomain of the relation R.
◼ Consider the relation R of our first example.
♦ The set B for this relation is: {Maths, Physics, Chemistry, Biology, Geography}
♦ So codomain of this R is : {Maths, Physics, Chemistry, Biology, Geography}
◼ Consider the relation R of our second example.
♦ The set B for this relation is: {3, 4, 5}
♦ So codomain of this R is : {3, 4, 5}
◼ Consider the relation R of our third example.
♦ The set B for this relation is: {1, 2, 3, 4, 5, 6}
♦ So codomain of this R is : {1, 2, 3, 4, 5, 6}
From the above four definitions, following 4 points can be noted:
(i) domain will contain only those elements belonging to Set A.
♦ all elements of A may not be present in domain.
(ii) codomain will contain only those elements belonging to Set B.
♦ all elements of B will be present in codomain.
(iii) range will contain only those elements belonging to Set B.
♦ all elements of B may not be present in range.
(iv) From (ii) and (iii), it is clear that:
range ⊂ codomain.
•
Once we understand the basics, there will not be any need to write all
the lengthy steps. We will be able to obtain the results using minimum
steps.
• The solved examples given below will demonstrate the process
Solved example 2.15
Let A = {1, 2, 3,...,14}. Define a relation R from A to A by
R = {(x, y) : 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and
range.
Solution:
1. The relation R is a set which contains ordered pairs of the form (x, y)
♦ 'x' should be from set A
♦ Since the relation is from A to A, 'y' should also be from set A
• The x and y in each ordered pair in R should satisfy the condition: 3x - y = 0
2. The given condition can be rearranged as: 3x = y
Let us take each possible value for x from set A:
• When x = 1,
♦ y = 3x = (3 × 1) = 3
♦ '3' is available in A
♦ So the first ordered pair in R is (1, 3)
• When x = 2,
♦ y = 3x = (3 × 2) = 6
♦ '6' is available in A
♦ So the second ordered pair in R is (2, 6)
• When x = 3,
♦ y = 3x = (3 × 3) = 9
♦ '9' is available in A
♦ So the third ordered pair in R is (3, 9)
• When x = 4,
♦ y = 3x = (3 × 4) = 12
♦ '12' is available in A
♦ So the fourth ordered pair in R is (4, 12)
• When x = 5,
♦ y = 3x = (3 × 5) = 15
♦ '15' is not available in A
♦ So the ordered pair (5, 15) does not satisfy the given relation.
✰ Note that (5, 15) will not be available in A × A also.
3. The set R will contain the four ordered pairs that we determined above. We can write:
R = {(1,3), (2,6), (3,9), (4,12)}
4. Domain is the set containing all the first elements in the ordered pairs of R. So we get:
Domain of R = {1, 2, 3, 4}
5. Codomain is the set from which we take the second elements of the ordered pairs in R. In effect, co domain is the set B.
• In our present case, since the relation is from A to A, we have A in place of B.
• So we get: codomain of R = {1, 2, 3,...,14}
6. Range is the set containing all the second elements in the ordered pairs of R.
• So we get: Range of R = {3, 6, 9, 12}
• We know that, a relation is defined from one set A to another set B
• But some times, the relation is defined from one set A to the same set A
• In such situations, we can use any one of the two statements below:
♦ Relation R from A to A
♦ Relation R on A
More solved examples are given at the link below:
In
the next
section, we will see functions.
Previous
Contents
Next
Copyright©2021 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment