Chapter 3 - Trigonometric Functions

In the previous section, we completed a discussion on relations and functions. In this chapter, we will see trigonometric functions.

• We have seen the basics of trigonometry in our previous classes. Details here.
• We will start our present discussion by deriving some interesting trigonometric identities. They can be written in steps:

1. Fig.3.1 below shows a right triangle ABC

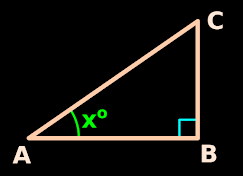Fig.3.1

• The angle at A is x^o
2. Applying Pythagoras theorem, we have: AB² + BC² = AC²
3. Dividing both sides by AC², we get: $\mathbf\small{\rm{\frac{AB^2}{AC^2}+\frac{BC^2}{AC^2}=\frac{AC^2}{AC^2}}}$
4. But $\mathbf\small{\rm{\frac{AB}{AC}}}$ is cos x. Also $\mathbf\small{\rm{\frac{BC}{AC}}}$ is sin x
• So we get: (cos x)² + (sin x)² = 1
5. Thus we get our first identity: cos²x + sin²x = 1
6. Consider again the result in (2).
Dividing both sides by BC², we get: $\mathbf\small{\rm{\frac{AB^2}{BC^2}+\frac{BC^2}{BC^2}=\frac{AC^2}{BC^2}}}$
7. But $\mathbf\small{\rm{\frac{AB}{BC}}}$ is cot x. Also $\mathbf\small{\rm{\frac{AC}{BC}}}$ is cosec x
• So we get: (cot x)² + 1 = (cosec x)²
8. Thus we get our second identity: cot²x + 1 = cosec²x
9. Consider again the result in (2).
Dividing both sides by AB², we get: $\mathbf\small{\rm{\frac{AB^2}{AB^2}+\frac{BC^2}{AB^2}=\frac{AC^2}{AB^2}}}$
10. But $\mathbf\small{\rm{\frac{BC}{AB}}}$ is tan x. Also $\mathbf\small{\rm{\frac{AC}{AB}}}$ is sec x
• So we get: 1 + (tan x)² = (sec x)²
11. Thus we get our third identity: 1 + tan²x = sec²x

---

Let us see some solved examples:

Solved example 3.1
Prove that $\mathbf\small{\rm{(\csc\theta-\cot\theta)^2=\frac{1-\cos\theta}{1+\cos\theta}}}$
Solution:
• Consider the RHS.
• Multiplying both numerator and denominator by (1 - cos 𝜃), we get:
$$\begin{eqnarray}
RHS &=& \frac{(1-\cos\theta)(1-\cos\theta)}{(1+\cos\theta)(1-\cos\theta)}      \nonumber \\
\Rightarrow RHS &=& \frac{(1-\cos\theta)^2}{1-\cos^2\theta}=\frac{(1-\cos\theta)^2}{\sin^2\theta} \nonumber \\
&=& \frac{1-2\cos\theta+\cos^2 \theta}{\sin^2\theta}=\frac{1}{\sin^2\theta}-\frac{2\cos\theta}{\sin^2\theta}+\frac{\cos^2 \theta}{\sin^2\theta} \nonumber \\
&=& \csc^2 \theta-2\csc\theta \cot\theta+\cot^2\theta \nonumber \\
&=& (\csc \theta-\cot\theta)^2 = LHS \nonumber
\end{eqnarray}$$

Solved example 3.2
Prove that: $\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}=2\sec A$
Solution:
• Consider the RHS.
• Multiplying both numerator and denominator by (1 - sin A), we get:
$$\begin{eqnarray}
LHS &=& \frac{\cos A(1-\sin A)}{(1+\sin A)(1-\sin A)}+\frac{(1+\sin A)(1-\sin A)}{\cos A(1-\sin A)}     \nonumber \\
\Rightarrow LHS &=& \frac{\cos A(1-\sin A)}{1-\sin^2 A}+\frac{1-\sin^2 A}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{\cos A(1-\sin A)}{\cos^2 A}+\frac{\cos^2 A}{\cos A(1-\sin A)}\nonumber \\
&=& \frac{(1-\sin A)}{\cos A}+\frac{\cos A}{(1-\sin A)} \nonumber \\
&=& \frac{(1-\sin A)^2+\cos^2 A}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{(1-2\sin A+\sin^2 A)+\cos^2 A}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{1-2\sin A+(\sin^2 A+\cos^2 A)}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{1-2\sin A+1}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{2-2\sin A}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{2(1-\sin A)}{\cos A(1-\sin A)} \nonumber \\
&=& \frac{2}{\cos A} \nonumber \\
&=& 2\sec A = RHS \nonumber
\end{eqnarray}$$

Solved example 3.3
Prove that $\frac{\tan\theta}{1-\cot\theta}+\frac{\cot\theta}{1-\tan\theta}=1+\sec\theta \csc\theta$
[Hint : Write the expression in terms of sin θ and cos θ]
Solution:
1. Consider the first term on LHS:
$$\begin{eqnarray}
\text{First term}&=& \frac{\tan\theta}{1-\cot\theta}\nonumber \\
&=& \frac{\frac{\sin\theta}{\cos\theta}}{1-\frac{\cos\theta}{\sin\theta}}\nonumber \\
&=& \frac{\frac{\sin\theta}{\cos\theta}}{\frac{\sin\theta-\cos\theta}{\sin\theta}}\nonumber \\
&=& \frac{\sin\theta}{\cos\theta}\times \frac{\sin\theta}{\sin\theta-\cos\theta}\nonumber \\
&=& \frac{\sin^2\theta}{\cos\theta(\sin\theta-\cos\theta)} \nonumber
\end{eqnarray}$$
2. Consider the second term of LHS:
\begin{eqnarray}
\text{Second term}&=& \frac{\cot\theta}{1-\tan\theta}\nonumber \\
&=& \frac{\frac{\cos\theta}{\sin\theta}}{1-\frac{\sin\theta}{\cos\theta}}\nonumber \\
&=& \frac{\frac{\cos\theta}{\sin\theta}}{\frac{\cos\theta-\sin\theta}{\cos\theta}}\nonumber \\
&=& \frac{\cos\theta}{\sin\theta}\times \frac{\cos\theta}{\cos\theta-\sin\theta}\nonumber \\
&=& \frac{\cos^2\theta}{\sin\theta(\cos\theta-\sin\theta)}\nonumber \\
&=& \frac{-\cos^2\theta}{\sin\theta(\sin\theta-\cos\theta)} \nonumber
\end{eqnarray}
3.Adding (1) and (2), we get:
\begin{eqnarray}
\text{LHS}&=& \frac{1}{(\sin\theta-\cos\theta)}\left[ \frac{\sin^2\theta}{\cos\theta}-\frac{\cos^2\theta}{\sin\theta}\right]\nonumber \\
&=& \frac{1}{(\sin\theta-\cos\theta)}\left[ \frac{\sin^3\theta-\cos^3\theta}{\sin\theta\cos\theta}\right]\nonumber \\
&=& \frac{1}{(\sin\theta-\cos\theta)}\left[ \frac{(\sin\theta-\cos\theta)(\sin^2\theta+\sin\theta\cos\theta+\cos^2\theta)}{\sin\theta\cos\theta}\right]\nonumber \\
[&\because& a^3-b^3=(a-b)(a^2+ab+b^2)]\nonumber \\
&=& \frac{(\sin^2\theta+\sin\theta\cos\theta+\cos^2\theta)}{\sin\theta\cos\theta}\nonumber \\
&=& \frac{(1+\sin\theta\cos\theta)}{\sin\theta\cos\theta}\nonumber \\
[&\because& \sin^2\theta+\cos^2\theta=1]\nonumber \\
&=& \frac{1}{\sin\theta\cos\theta}+1\nonumber \\
&=& 1+\sec\theta\csc\theta=RHS \nonumber
\end{eqnarray}

---

Link to some more solved examples is given below:

Solved examples 3.4 to 3.10

---

In the next section, we will see measurement of angles.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com