Chapter 1.7 - Difference of Sets

In the previous section, we saw intersection of sets. In this section, we will see difference of sets.

Difference of sets

• This can be explained in 9 steps:
1. Let A and B be any two sets.
• We perform an operation called ‘difference of sets’ between A and B.
2. The set which is formed as a result of that operation,
    ♦ will contain only those elements of A which do not belong to B.
• This can be explained further as follows:
    ♦ The resulting set can contain elements of A.
    ♦ The resulting set can not contain any element of B.
    ♦ The resulting set can not contain any element which is common to A and B.
3. The symbol ‘－’ is used to represent difference.
• So the difference of A and B can be represented as A － B.
    ♦ It is read as: A minus B.
4. Let us see some examples:
A = {2, 4, 6, 8, 10} and B = {2, 4, 6, 12, 14}. Find A － B.
Solution:
• A － B can contain elements of A.
• A － B can not contain any element of B.
    ♦ So we can right away discard set B.
• Also, A － B cannot contain any element which is common to both A and B.
    ♦ So we can discard 2, 4 and 6 from A.
• Thus we get: A － B = {8, 10}
• We can represent this difference using Venn diagrams also.
    ♦ Fig.1.16(a) below shows A and B before the difference.
    ♦ Fig.1.16(b) shows the new set which is A － B.

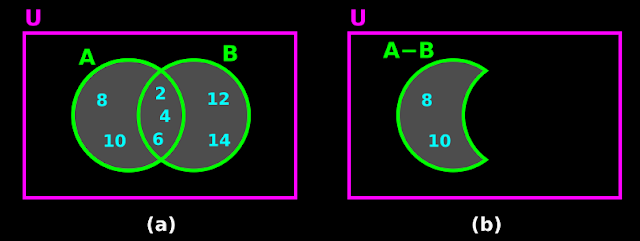Fig.1.16

5. In the above example, find B － A
Solution:
• B － A can contain elements of B.
• B － A cannot contain any element of A.
    ♦ So we can right away discard set A.
• Also, B － A cannot contain any element which is common to both B and A.
    ♦ So we can discard 2, 4 and 6 from B.
• Thus we get: B － A = {12, 14}
• We can represent this difference using Venn diagrams also.
    ♦ Fig.1.17(a) below shows A and B before the difference.
    ♦ Fig.1.17(b) shows the new set which is B － A.

Fig.1.17

6. The above two examples show that:
    ♦ A － B
    ♦ is not equal to
    ♦ B － A
• So we must be careful about the order while specifying the difference.
• We must clearly examine the two sets:
    ♦ The set on the left side of '－' sign.
    ♦ The set on the right side of '－' sign.
7. Another example:
Let V = {a, e, i, o, u} and B = {a, i, k, u}. Show that V － B ≠ B － V 
Solution:
(i) V － B can contain elements of V.
• V － B cannot contain any element of B.
    ♦ So we can right away discard set B.
• Also, V － B cannot contain any element which is common to both V and B.
    ♦ So we can discard a, i and u from V.
• Thus we get: V － B = {e, o}
(ii) B － V can contain only elements of B.
• B － V cannot contain any element of V.
    ♦ So we can right away discard set V.
• Also, B － V cannot contain any element which is common to both V and B.
    ♦ So we can discard a, i and u from B.
• Thus we get: V － B = {k}
(iii) Thus we see that: V － B ≠ B － V
8. Thus we can write the definition:

Definition 8: The difference of two sets A and B is the set C which consists of all those elements which belong to A but not to B.

9. Let us see the relation between intersection and difference. It can be written in 4 steps:
(i) Consider two sets A and B.
• We can performs the operations of intersection and difference on the two sets.
(ii) As a result of those operations, we get three different sets:
A － B, B － A and A ∩ B
(Recall that, A ∩ B is same as B ∩ A. So the operation of intersection will give only one set)
(iii) Fig.1.18(a) below shows the two sets A and B before the operations.
• Fig.b shows the three resulting sets.

Fig.1.18

(iv) We see that, the three resulting sets do not have any overlapping parts.
◼ Thus we can write:
A － B, B － A and A ∩ B are mutually disjoint. They will never have any common elements.

Now we will see some solved examples:
Solved example 1.26
Find the union of each of the following pairs of sets :
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = [ a, e, i, o, u} B = {a, b, c}
(iii) A = {x : x is a natural number and multiple of 3}
B = {x : x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 < x ≤ 6 }
B = {x : x is a natural number and 6 < x < 10 }
(v) A = {1, 2, 3}, B = ɸ
Solution:
(i) X ∪ Y = {1, 2, 3, 5}
(ii) A ∪ B = {a, b, c, e, i, o, u}
(iii) In roster form, A = {3, 6, 9, 12, . . .}
• In roster form, B = {1, 2, 3, 4, 5}
• So A ∪ B = {x : x = 1, 2, 4, 5 or a multiple of 3}
(iv) In roster form, A = {2, 3, 4, 5, 6}
• In roster form, B = {7, 8, 9}
• So A ∪ B = {2, 3, 4, 5, 6, 7, 8, 9}
(v) A ∪ B = {1, 2, 3}

Solved example 1.27
Let A = { a, b }, B = {a, b, c}. Is A ⊂ B ? What is A ∪ B ?
Solution:
• All elements of A are present in B. So A ⊂ B
• A ∪ B = {a, b, c} = B

Solved example 1.28
If A and B are two sets such that A ⊂ B, then what is A ∪ B
Solution:
If A is a subset of B, then A ∪ B will be B

Solved example 1.29
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 } and D = { 7, 8, 9, 10 }; find
(i) A ∪ B  (ii) A ∪ C  (iii) B ∪ C  (iv) B ∪ D  (v) A ∪ B ∪ C  (vi) A ∪ B ∪ D  (vii) B ∪ C ∪ D
Solution:
(i) A ∪ B = {1, 2, 3, 4, 5, 6}
(ii) A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(iii) B ∪ C = {3, 4, 5, 6, 7, 8}
(iv) B ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}
(v) A ∪ B = {1, 2, 3, 4, 5, 6}
   ♦ So A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(vi) A ∪ B = {1, 2, 3, 4, 5, 6}
   ♦ So A ∪ B ∪ D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(vii) B ∪ C = {3, 4, 5, 6, 7, 8}
   ♦ So B ∪ C ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}

Solved example 1.30
Find the intersection of each pair of sets of example 1.26 above.
Solution:
(i) X ∩ Y = {1, 3}
(ii) A ∩ B = {a}
(iii) In roster form, A = {3, 6, 9, 12, . . .}
• In roster form, B = {1, 2, 3, 4, 5}
• So A ∩ B = {3}
(iv) In roster form, A = {2, 3, 4, 5, 6}
• In roster form, B = {7, 8, 9}
• So A ∩ B = ɸ
(v) A ∩ B = ɸ {1, 2, 3}

Solved example 1.31
If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}; find
(i) A ∩ B  (ii) B ∩ C  (iii) A ∩ C ∩ D  (iv) A ∩ C  (v) B ∩ D  (vi) A ∩ (B ∪ C) (vii) A ∩ D
(viii) A ∩ (B ∪ D)  (ix) ( A ∩ B ) ∩ ( B ∪ C )  (x) (A ∪ D) ∩ (B ∪ C)
Solution:
(i) A ∩ B = {7, 9, 11}
(ii) B ∩ C = {11, 13}
(iii) A ∩ C = {11}
   ♦ So A ∩ C ∩ D = ɸ
(iv) A ∩ C = {11}
(v) B ∩ D = ɸ
(vi) B ∪ C = {7, 9, 11, 13, 15}
   ♦ So A ∩ (B ∪ C) = {7, 9, 11}
(vii) A ∩ D = ɸ
(viii) B ∪ D = {7, 9, 11, 13, 15, 17}
   ♦ So A ∩ (B ∪ D) = {7, 9, 11}
(ix) A ∩ B = {7, 9, 11}
• B ∪ C = {7, 9, 11, 13, 15}
   ♦ So ( A ∩ B ) ∩ ( B ∪ C )   = {7, 9, 11}
(x) A ∪ D = {3, 5, 7, 9, 11, 15, 17}
• B ∪ C = {7, 9, 11, 13, 15}
   ♦ So ( A ∩ B ) ∩ ( B ∪ C ) = {7, 9, 11, 15}

---

The link below gives some solved examples:

Solved examples 1.32 to 1.37

---

In the next section, we will see complement of a set.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com