Chapter 1.5 - Venn Diagrams

In the previous section, we saw power set and universal set. In this section, we will see Venn diagrams. Later in this section, we will also see union of sets.

• Basics of Venn diagrams can be explained in 3 steps:
1. In Venn diagrams, the universal set is represented by a rectangle.
    ♦ All other sets are represented by circles.
• We know that, all other sets will be subsets of U.
    ♦ So the circles are enclosed within the rectangle.
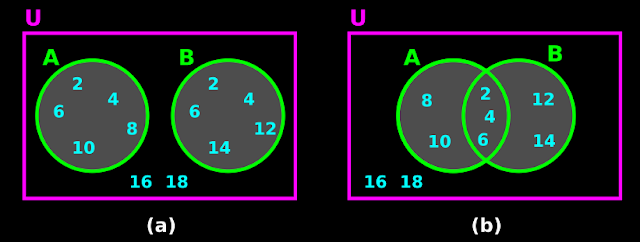
2. In fig.1.4(a) below,
    ♦ Set A = {2, 4, 6, 8, 10}
    ♦ Set B = {2, 4, 6, 12, 14}

Fig.1.4

• All elements of A and all elements of B belong to U.
• We see that, both A and B possess 2, 4 and 6.
• So we are inclined to think that, U possess two 2, two 4 and two 6
3. Recall that, in sets, repeating elements are written only once. This is applicable to universal set also.
• So the fig.a must be modified. The modified fig. is shown in fig.1.4(b)
• In the modified fig., we see that,
    ♦ The two circles over lap.
        ✰ But the circle A encloses all elements of set A.
        ✰ Also, the circle B encloses all elements of set B.
• Thus we get:
A = {2, 4, 6, 8, 10}
B = {2, 4, 6, 12, 14}
U = {2, 4, 6, 8, 10, 12, 14, 16, 18}

---

Operations on sets

• Consider the familiar operation of addition that we perform on two numbers say 5 and 12.
    ♦ As a result of the operation, we get a new number 17
• Subtraction is another operation that we perform on two numbers.
• We can perform certain operations on sets also.
    ♦ As a result of such an operation, we get a new set.
• We will now discuss about those operations that we perform between two sets.

Union of sets

• This can be explained in 8 steps:
1. Let A and B be any two sets.
• We perform an operation called ‘union of sets’ between A and B.
2. The set which is formed as a result of that operation,
    ♦ will contain all the elements of A.
    ♦ will contain all the elements of B.
3. But there is an important point to remember. It can be written in 3 steps:
(i) Some elements may be present in both the sets A and B.
(ii) So when we write the elements of A and B together, such elements will appear twice.
(iii) However, in the resultant set, those repeating elements should be written only once.
4. The symbol ‘∪’ is used to represent union.
• So the union of A and B can be represented as A ∪ B
5. Let us see some examples:
A = {2, 4, 6, 8, 10} and B = {2, 4, 6, 12, 14}. Find A ∪ B.
Solution:
• A ∪ B must contain all the elements of A and B.
• The elements 2, 4 and 6 appear in both A and B. They must be written only once in A ∪ B.
• Thus we get: A ∪ B = {2, 4, 6, 8, 10, 12, 14}
• We can represent this union using Venn diagrams also.
    ♦ Fig.1.5(a) below shows A and B before the union.
    ♦ Fig.1.5(b) shows the new set which is A ∪ B.

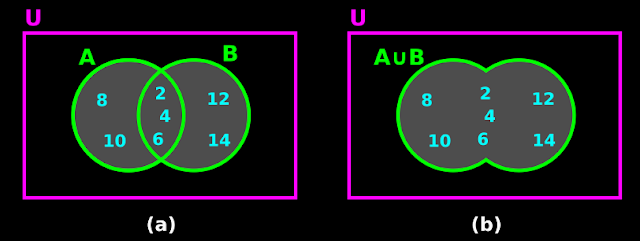Fig.1.5

6. Another example:
Let A = { a, e, i, o, u } and B = { a, i, u }. Show that A ∪ B = A
Solution:
• A ∪ B must contain all the elements of A and B.
• The elements a, i and u appear in both A and B. They must be written only once in A ∪ B.
• Thus we get: A ∪ B = {a, e, i, o, u}
    ♦ We see that, A ∪ B is same as A.
• We can represent this union using Venn diagrams also.
    ♦ Fig.1.6(a) below shows A and B before the union.
    ♦ Fig.1.6(b) shows the new set which is A ∪ B

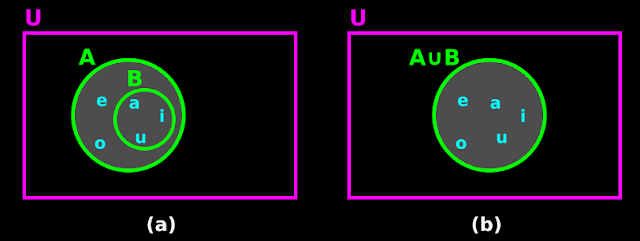Fig.1.6

• We see that, all elements of B are contained in A. So B ⊂ A
    ♦ When the union takes place, the resulting set is same as the superset
    ♦ We can write: B ⊂ A ⇒ A ∪ B = A
7. One more example:
Let X = {Ram, Geeta, Akbar} be the set of students of Class XI, who are in school hockey team. Let Y = {Geeta, David, Ashok} be the set of students from Class XI who are in the school football team. Find X ∪ Y and interpret the set.
Solution:
• We have: X ∪ Y = {Ram, Geeta, Akbar, David, Ashok}
• We see that:
The set X ∪ Y consists of members who are in the hockey team or football team or both
8. Thus we can write the definition:

Definition 6: The union of two sets A and B is the set C which consists of all those elements which are either in A or in B (including those which are in both).

• In symbols, we write: A ∪ B = { x : x ∈ A or x ∈ B }

---

Some Properties of the Operation of Union

1. A ∪ B = B ∪ A (Commutative law)
• This is obvious from fig.1.5 above.
    ♦ Both A ∪ B and B ∪ A will give the same result in fig.1.5(b)
2. (A ∪ B) ∪ C = A ∪ (B ∪ C) (Associative law)
• This can be proved in 3 steps, using Venn diagrams.
(i) Fig.1.7(a) below shows the three sets A, B and C.

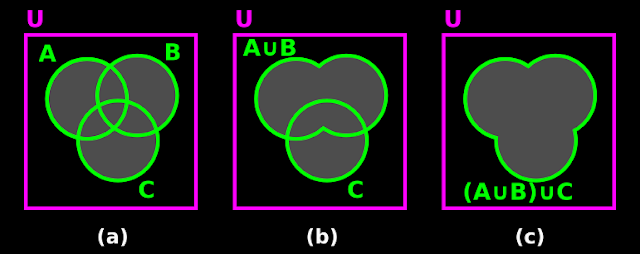Fig.1.7

• Fig.b shows (A ∪ B) and C.
    ♦ Fig.c shows the union between (A ∪ B) and C.
(ii) Fig.1.8(a) below shows the three sets A, B and C.

Fig.1.8

• Fig.b shows A and (B ∪ C).
    ♦ Fig.c shows the union between A and (B ∪ C).
(iii) We see that
    ♦ Fig.1.7(c)
    ♦ is same as
    ♦ Fig.1.8(c)
3. A ∪ ɸ = A (Law of identity element, ɸ is the identity of ∪)
• This is obvious because,
    ♦ A ∪ ɸ must contain all elements of A and ɸ.
    ♦ That means, A ∪ ɸ will contain only the elements of A.
4. A ∪ A = A (Idempotent law)
• This is obvious because,
    ♦ A ∪ A must contain all elements of A and A.
    ♦ But we know that, repeating elements are written only once.
    ♦ That means, A ∪ A will contain only the elements of A.
(5) U ∪ A = U (Law of U)
• This is obvious because,
    ♦ U ∪ A must contain all elements of U and A.
    ♦ U already contains A.
    ♦ But we know that, repeating elements are written only once.
    ♦ That means, U ∪ A will be same as U.

---

In the next section, we will see intersection of sets

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com