In the previous section, we saw complement of sets. In this section, we will see some practical problems involving sets.
• First we will see those problems which involve two sets. In later sections, we will see problems which involve three sets.
• When only two sets are involved, some basics can be written using an example. It can be written in 7 steps:
1. The cricket coach wants to make a team of cricket players. He approaches a class of 35 students and interviews each of them. He finds that, 24 students like to play cricket.
2. After a few days, the football coach approaches the same class. He wants to make a football team. He finds that, 16 students like to play football.
3. The next day, the two coaches have a chat.
• The cricket coach says:
24 students like to play cricket. I can make a cricket team by picking the best among them.
• The football coach says:
16 students like to play football. I can make a football team by picking the best among them.
4. But now a problem arises:
♦ (24 + 16) is 40
♦ The strength of the class is only 35
• How is that possible?
5. We can solve this problem by using set theory. It can be written in 7 steps:
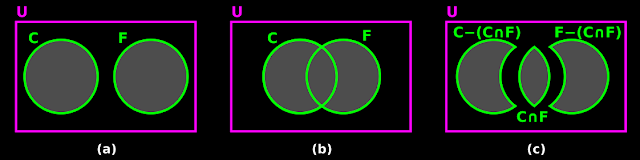
(i) The Venn diagram in fig.1.24(a) below shows two sets:
 |
| Fig.1.24 |
• All the names in the list possessed by the cricket coach are written inside the C circle.
• All the names in the list possessed by the football coach are written inside the F circle.
(ii) But some names appear in both the circles. If we count the total number, we will get (24 + 16) = 40.
• We know that, inside U, elements must appear only once. So we modify the diagram as shown in fig.b
(iii) Now the total number becomes 35.
• It is clear that, the total number of 40 was wrongly calculated because, some students wanted to be in both teams.
(iv) The modified Venn diagram in fig.b is split into three disjoint sets. This is shown in fig.c
• From the Venn diagram in fig.c, three points become clear. They are numbered as (a), (b) and (c):
(a) The number of students who like to play both games is:
♦ The number of elements in the set C ∩ F
♦ This is equal to: n(C ∩ F)
(b) The number of students who like to play cricket only is:
♦ The number of elements in the set [C – (C ∩ F)]
♦ This is equal to: n(C) - n(C ∩ F)
(c) The number of students who like to play football only is:
♦ The number of elements in the set [F – (C ∩ F)]
♦ This is equal to: n(F) - n(C ∩ F)
(v) Now we can equate the numbers:
♦ The number of elements in the union (C ∪ F)
♦ must be equal to
♦ The total number of elements in the three disjoint sets.
(vi) Thus we get:
n(C ∪ F) = n(C) - n(C ∩ F) + n(C ∩ F) + n(F) - n(C ∩ F)
⇒ n(C ∪ F) = n(C) + n(F) - n(C ∩ F)
(vii) Substituting the known values, we get:
35 = 24 + 16 - n(C ∩ F)
⇒ n(C ∩ F) = 5
• That mean, 5 students like to be in both the teams.
6. The equation in 5(vi) above can be written in a general form:
Eq.1.1: n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
• There are four quantities in this equation. If any three is known, the unknown quantity can be easily calculated.
7. An important point can be written in 2 steps:
(i) In this problem, every student wants to play.
◼ This fact is written as:
Each student likes to play at least one of the two games.
(ii) If one or more students do not want to be part of any team, the Eq.1.1 will not work.
♦ In such cases, we will have to use complement sets.
♦ We will see such problems later.
Let us see another example:
In a school there are 20 teachers who teach mathematics or physics. Of
these, 12 teach mathematics and 4 teach both physics and mathematics. Every teacher can teach at least one of the two subjects. How many teach physics ?
Solution:
1. Naming of sets:
• Let M denote the set of teachers who can teach mathematics
♦ So M will contain the names of all teachers who can teach mathematics
• Let P denote the set of teachers who can teach physics
♦ So P will contain the names of all teachers who can teach physics
2. The set (M ∩ P) will contain the names of those teachers who are able to teach both subjects
3. Applying Eq.1.1, we get:
n(M ∪ P) = n(M) + n(P) - n(M ∩ P)
• Substituting the known values, we get:
20 = 12 + n(P) - 4
⇒ n(P) = 12
4. So we can write: 12 teachers can teach physics only.
Another example:
If X and Y are two sets such that X ∪ Y has 50 elements, X has 28 elements and Y has 32 elements, how many elements does X ∩ Y have ?
Solution:
1. Applying Eq.1.1, we get:
n(X ∪ Y) = n(X) + n(Y) - n(X ∩ Y)
• Substituting the known values, we get:
50 = 28 + 32 - n(X ∩ Y)
⇒ n(X ∩ Y) = 10
Another example:
There are 200 individuals with a skin disorder, 120 had been exposed to the chemical C1, 50 to chemical C2 and 30 to both the chemicals C1 and C2. Every individual has been exposed to at least one chemical. Find the number of individuals exposed to
(i) Chemical C1 but not chemical C2
(ii) Chemical C2 but not chemical C1
(iii) Chemical C1 or chemical C2
Solution:
1. Tests conducted by three agencies:
• An agency conducts tests on people in a locality.
♦ They want to find the number of people exposed to chemical C1.
♦ They find the presence of C1 in 120 individuals.
♦ The set C1 prepared by this agency, contains those 120 names.
• A second agency conducts tests on people in that locality.
♦ They want to find the number of people exposed to chemical C2.
♦ They find the presence of C2 in 50 individuals.
♦ The set C2 prepared by this agency, contains those 50 names.
• A third agency conducts tests on people in that locality.
♦ They want to find the number of people exposed to both C1 and C2.
♦ They find the presence of both C1 and C2 in 30 individuals.
• Adding the numbers in the three sets, we get: (120 + 50 + 30) = 200
2. But it is clear that, the set C1 will contain the names in the third set also.
• So the number of individuals exposed to C1 only is (120 - 30) = 90
• This number is in fact [n(C1) - n(C1 ∩ C1)].
• This is the number of elements in the left side crescent in fig.1.25(b) below.
• So the answer to the first part is 90
 |
| Fig.1.25 |
3. In a similar way, the set C2 will contain the names in the third set also.
• So the number of individuals exposed to C2 only is (50 - 30) = 20
• This number is in fact [n(C2) - n(C1 ∩ C2)].
• This is the number of elements in the right side crescent in fig.1.25(b).
• So the answer to the second part is 20.
4. In the third part, the word 'or' is present. This indicates union.
• The union must include three items:
♦ Those exposed to C1 only.
♦ Those exposed to both C1 and C2.
♦ Those exposed to C2 only.
• It is the union of the three portions in fig.1.25(b)
• So the answer to the third part is (90 + 30 + 20) = 140
♦ This is a direct application of Eq.1.1
♦ The only unknown is n(A ∪ B)
The link below gives some solved examples:
Now we will see a practical problem which involves two sets and complement sets.
In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple as well as orange juice. Find how many students were taking neither apple juice nor orange juice.
Solution:
1. Naming of sets:
• Let U denote the set of all 400 students in the school.
♦ So U will contain the names of all the 400 students in the school.
• Let A denote the set of students who like apple juice.
♦ So A will contain the names of all students who like apple juice.
• Let O denote the set of students who like orange juice.
♦ So O will contain the names of all students who like orange juice.
2. The set (A ∩ O) will contain the names of those students who like both apple juice and orange juice.
3. Applying Eq.1.1, we get:
n(A ∪ O) = n(A) + n(O) - n(A ∩ O)
• Substituting the known values, we get:
n(A ∪ O) = 100 + 150 - 75
⇒ n(A ∪ O) = 175
4. A ∪ O is a union. It contains the name of all the students who like at least one juice.
• So the set which contains the names of all the students who like neither apple juice nor orange juice will be (A ∪ O)'
• This complement set will be same as: [U - (A ∪ O)]
• Number of elements in this complement set can be calculated as:
n(U) - n(A ∪ O) = (400 - 175) = 225
Another example:
In a survey of 600 students in a school, 150 students were found to be taking tea
and 225 taking coffee, 100 were taking both tea and coffee. Find how many
students were taking neither tea nor coffee?
Solution:
1. Naming of sets:
• Let U denote the set of all 600 students in the school.
♦ So U will contain the names of all the 600 students in the school.
• Let T denote the set of students who like tea.
♦ So T will contain the names of all students who like tea.
• Let C denote the set of students who like coffee.
♦ So C will contain the names of all students who like coffee.
2. The set (T ∩ C) will contain the names of those students who like both tea and coffee.
3. Applying Eq.1.1, we get:
n(T ∪ C) = n(T) + n(C) - n(T ∩ C)
• Substituting the known values, we get:
n(T ∪ C) = 150 + 225 - 100
⇒ n(T ∪ C) = 275
4. T ∪ C is a union. It contains the name of all the students who like at least one drink.
• So the set which contains the names of all the students who like neither tea nor coffee will be (T ∪ C)'
• This complement set will be same as: [U - (T ∪ C)]
• Number of elements in this complement set can be calculated as:
n(U) - n(T ∪ C) = (600 - 275) = 325
In the next
section, we will see some interesting relations between sets. After that, we will see the practical problems which involves three sets.
Previous
Contents
Next
Copyright©2021 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment