In the previous section, we saw some practical problems involving sets. In this section, we will see some interesting relations between sets. We will see them in the form of solved examples.
Solved example 1.56
Show that A ∪ B = A ∩ B implies A = B
Solution:
• We will solve this problem in two parts: Part (a) and Part (b).
♦ In part (a), we prove that A ⊂ B
♦ In part (b), we prove that B ⊂ A
Part (a):
1. Let a be an element of A.
♦ Using symbols, we write this as: a ∈ A
2. Since a is an element of A, the same a will be an element of A ∪ B also.
♦ Using symbols, we write this as: a ∈ A ∪ B
3. Given that A ∪ B = A ∩ B
♦ So a will be an element of A ∩ B also.
♦ Using symbols, we write this as: a ∈ A ∩ B
4. A ∩ B is the set which contains only the common elements of A and B.
♦ So, if a is an element of A ∩ B, the same a will be an element of B also.
♦ Using symbols, we write this as: a ∈ B
5. Comparing two statements:
♦ In (1), we wrote that, a is an element of A.
♦ In (4), we saw that, the same a is an element of B also.
• That means, every element in A is an element of B also.
♦ Using symbols, we write this as: A ⊂ B
Part (b):
1. Let b be an element of B.
♦ Using symbols, we write this as: b ∈ B
2. Since b is an element of B, the same b will be an element of A ∪ B also.
♦ Using symbols, we write this as: b ∈ A ∪ B
3. Given that A ∪ B = A ∩ B
♦ So b will be an element of A ∩ B also.
♦ Using symbols, we write this as: b ∈ A ∩ B
4. A ∩ B is the set which contains only the common elements of A and B.
♦ So, if b is an element of A ∩ B, the same b will be an element of A also.
♦ Using symbols, we write this as: b ∈ A
5. Comparing two statements:
♦ In (1), we wrote that, b is an element of B.
♦ In (4), we saw that, the same a is an element of A also.
• That means, every element in B is an element of A also.
♦ Using symbols, we write this as: B ⊂ A
◼ In part (a), we proved that, A ⊂ B
◼ In part (b), we proved that, B ⊂ A
◼ This is possible only if the two sets are the same. So we can write: A = B
Solved example 1.57
In each of the following, determine whether the statement is true or false. If it is
true, prove it. If it is false, give an example.
(i) If x ∈ A and A ∈ B , then x ∈ B
(ii) If A ⊂ B and B ∈ C , then A ∈ C
(iii) If A ⊂ B and B ⊂ C , then A ⊂ C
(iv) If A ⊄ B and B ⊄ C , then A ⊄ C
(v) If x ∈ A and A ⊄ B , then x ∈ B
(vi) If A ⊂ B and x ∉ B , then x ∉ A
Solution:
(i) If x ∈ A and A ∈ B , then x ∈ B
This is false. Let us see an example:
• A = {1, 2}, B = {3, {1, 2}, 4}
♦ Here A is an element of B.
♦ But '1' and '2' are not elements of B.
(ii) If A ⊂ B and B ∈ C , then A ∈ C
This is false. Let us see an example:
A = {1, 2}, B = {1, 2, 3}, C = {4, {1, 2, 3}, 5}
♦ Here B is an element of C.
♦ But {1, 2} is not an element of C.
(iii) If A ⊂ B and B ⊂ C , then A ⊂ C
This is true. Proof can be written in 3 steps:
1. Let a be an element of A.
♦ Using symbols, we write this as: a ∈ A
2. Given that A ⊂ B
♦ So all elements of A are present in B.
♦ So a ∈ B
3. Given that B ⊂ C
♦ So all elements of B are present in C.
♦ So a ∈ C
• Thus we get A ⊂ C
◼ The Venn diagram in fig.1.26(a) also proves this.
♦ The circle B encloses circle A. This is because A ⊂ B
♦ The circle C encloses circle B. This is because B ⊂ A
♦ So the circle C automatically encloses circle A, indicating A ⊂ C
 |
| Fig.1.26 |
This is false. Let us see an example:
• A = {1, 2}, B = {2, 3, 4}, C = {1, 2, 3, 5}
♦ Here A ⊄ B and B ⊄ C
♦ But A ⊂ C
◼ The Venn diagram in fig.1.26(b) also proves that this is false.
♦ The circle B does not enclose circle A because A ⊄ B
♦ The circle C does not enclose circle B because B ⊄ C
♦ But the circle C can enclose circle A because A ⊂ C
(v) If x ∈ A and A ⊄ B , then x ∈ B
This is false. It can be written in steps:
1. Given that x is an element of A.
2. Given that A is not a subset of B. So all elements of A are not present in B.
3. So x need not be present in B.
Let us see an example:
• A = {1, 2}, B = {2, 3, 4}
♦ Here A ⊄ B
♦ Also, '1' is not present in B.
(vi) If A ⊂ B and x ∉ B , then x ∉ A.
This is true. It can be proved in 2 steps:
1. Given that A is a subset of B. So all elements of A will be present in B.
2. So if x is not present in B, it cannot be present in A.
Solved example 1.58
Show that the following four conditions are equivalent :
(i) A ⊂ B (ii) A – B = ɸ (iii) A ∪ B = B (iv) A ∩ B = A
Solution:
Part (a):
• In this part, we prove that: A ⊂ B ⇒ A – B = ɸ
♦ It can be proved in 4 steps:
1. To find A - B, we first discard all elements of B.
2. Then we discard elements which are common in both A and B.
3. But when we discard the elements in B, we automatically discard the following two items:
♦ Common elements mentioned in (2).
♦ All elements of A.
4. So after the operation A - B, none of the elements of either A or B will remain.
• So we can write:
If A ⊂ B, the difference A - B will be a null set.
• In other words, A ⊂ B ⇒ A – B = ɸ
Part (b):
• In this part, we prove that: A ⊂ B ⇒ A ∪ B = B
♦ It can be proved in 4 steps:
1. To find A ∪ B, we write all elements of A and B together, but repeating elements will be written only once.
2. Here, all elements of A will be repeating. So none of the elements of A need to be considered.
3. All we need to do is: Write the elements of B.
4. So we can write: A ⊂ B ⇒ A ∪ B = B
Part (c):
In this part, we prove that: A ⊂ B ⇒ A ∩ B = A
♦ It can be proved in 4 steps:
1. To find A ∩ B, we write all elements which are common to both A and B.
2. Here, all elements of A are the common elements. In fact, they are the only common elements.
3. All we need to do is: Write the elements of A.
4. So we can write: A ⊂ B ⇒ A ∩ B = A
◼ Thus we see that, all given conditions are equivalent.
Solved example 1.59
Assume that P(A) = P(B). Show that A = B
Solution:
• We will solve this problem in two parts: Part (a) and Part (b).
♦ In part (a), we prove that A ⊂ B
♦ In part (b), we prove that B ⊂ A
Part (a):
1. P(A) will contain all subsets of A.
• So P(A) will contain A.
• Using symbols, we write this as: A ∈ P(A)
2. If A is an element of P(A), the same A will be an element of P(B) also.
♦ Because, it is given that P(A) = P(B)
• Using symbols, we write this as:
A ∈ P(A) ⇒ A ∈ P(B) [∵ P(A) = P(B)]
3. If A is an element of P(B), A will be a subset of B.
• Using symbols, we write this as: A ∈ P(B) ⇒ A ⊂ B
◼ Thus we proved that A ⊂ B
Part (b):
1. P(B) will contain all subsets of B.
• So P(B) will contain B.
• Using symbols, we write this as: B ∈ P(B)
2. If B is an element of P(B), the same B will be an element of P(A) also.
♦ Because, it is given that P(A) = P(B)
• Using symbols, we write this as:
B ∈ P(B) ⇒ B ∈ P(A) [∵ P(A) = P(B)]
3. If B is an element of P(A), B will be a subset of A.
• Using symbols, we write this as: B ∈ P(A) ⇒ B ⊂ A
◼ Thus we proved that B ⊂ A
• So we get: A ⊂ B and B ⊂ A
♦ This is possible only if A and B are equal.
◼ That means, A = B
Solved example 1.60
Is it true that for any sets A and B, P(A) ∪ P(B) = P(A ∪ B)? Justify your answer.
Solution:
This is false. Let us see an example. It can be written in steps:
1. Let A = {1, 2} and B = {2, 3}
• Then the power sets are:
♦ P(A) = {{1}, {2}, {1, 2}, ɸ}
♦ P(B) = {{2}, {3}, {2, 3}, ɸ}
2. So P(A) ∪ P(B) will be: {{1}, {2}, {3}, {1, 2}, {2, 3}, ɸ}
3. (A ∪ B) will be: {1, 2, 3}
• Then the power set of (A ∪ B) will be:
P(A ∪ B) = {{1}, {2}, {3}, {1, 2, 3}, {1, 2}, {2, 3}, {1, 3}, ɸ}
4. We see that, result in (2) is different from result in (3).
Solved example 1.61
Show that for any sets A and B,
A - B = A ∩ B'
Solution:
1. Consider the LHS: A - B
♦ To find A - B, we discard all elements of B.
♦ Then we discard those elements of A which are present in B also.
• The result will be the left side crescent in fig.1.27(b) below:
 |
| Fig.1.27 |
2. Consider the RHS A ∩ B'
• B' is shown in fig.1.28(a) below. It is the red shaded portion.
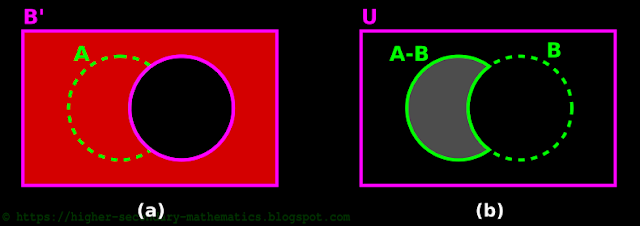 |
| Fig.1.28 |
• We want the intersection of two regions:
♦ Region B'
♦ Region A
3. The resulting intersection is the region,
♦ Where there is shading from both regions B' and A.
• So the result will be as in fig.1.28(b)
4. We see that:
Fig.1.27(b) is same as fig.1.28(b)
◼ So we can write: A - B = A ∩ B'
◼ Similarly, we can prove that: B - A = B ∩ A'
Solved example 1.62
Show that for any sets A and B,
(a) A = (A ∩ B) ∪ (A – B)
(b) A ∪ (B – A) = (A ∪ B)
Solution:
Part (a):
1. We have to prove that A = (A ∩ B) ∪ (A – B)
• Consider (A - B) in the RHS
• From the results in the previous solved example 1.61, we can write (A ∩ B') in the place of (A - B)
2. So the RHS becomes:
(A ∩ B) ∪ (A ∩ B')
3. Now recall the distributive law of intersection (Fig.1.14 of section 1.6):
X ∩ (Y ∪ Z) = (X ∩ Y) ∪ (X ∩ Z)
• The RHS in this law is similar to the result written in (2)
• So the result in (2) becomes: A ∩ (B ∪ B')
4. So the question becomes:
Prove: A = A ∩ (B ∪ B')
5. Consider (B ∪ B') in the RHS
• (B ∪ B') is U
• So the RHS in (4) becomes: A ∩ U
6. But A ∩ U is A
• So LHS and RHS are equal.
Part (b):
1. We have to prove that A ∪ (B – A) = (A ∪ B)
• Consider (B - A) in the LHS.
• From the results in the previous solved example 1.61, we can write (B ∩ A') in the place of (B - A)
2. So the LHS becomes:
A ∪ (B ∩ A')
3. Now recall the distributive law of union:
X ∪ (Y ∩ Z) = (X ∪ Y) ∩ (X ∪ Z)
• The LHS in this law is similar to the result written in (2)
• So the result in (2) becomes: (A ∪ B) ∩ (A ∪ A')
4. So the question becomes:
Prove: (A ∪ B) ∩ (A ∪ A') = (A ∪ B)
5. Consider (A ∪ A') in the RHS
• (A ∪ A') is U
• So the LHS in (4) becomes: (A ∪ B) ∩ U
6. But (A ∪ B) ∩ U is (A ∪ B)
• So LHS and RHS are equal.
Alternate method using Venn diagrams:
1. Fig.1.29(a) below shows our familiar 'Venn diagram of two sets'.
 |
| Fig.1.29 |
2. Fig.1.29(b) shows the three portions separated from each other. This is also familiar to us.
◼ It is clear that, the union of
♦ left crescent portion
♦ and the middle portion
♦ will give set A
• This proves part (a): A = (A ∩ B) ∪ (A – B)
3. From part (a), we have: A = (A ∩ B) ∪ (A – B)
• So A ∪ (B – A) = (A ∪ B) is same as: (A ∩ B) ∪ (A – B) ∪ (B – A)
♦ This is the union of the three portions in fig.1.29(b)
• The union of those three portions will give (A ∪ B)
• This proves part (b): A ∪ (B – A) = (A ∪ B)
Solved example 1.63
Using properties of sets, show that
(a) A ∪ ( A ∩ B ) = A
(b) A ∩ ( A ∪ B ) = A.
Solution:
Part (a):
1. We have to prove that A ∪ ( A ∩ B ) = A
• Consider the LHS. Recall the distributive law of union:
X ∪ (Y ∩ Z) = (X ∪ Y) ∩ (X ∪ Z)
2. Applying this law, the LHS becomes:
(A ∪ A) ∩ (A ∪ B)
3. But (A ∪ A) is A
• So the LHS becomes:
A ∩ (A∪B)
4. But A ∩ (A∪B) is A
• So the LHS becomes A
5. Thus we get LHS = RHS
Part (b):
1. We have to prove that A ∩ ( A ∪ B ) = A
• Consider the LHS. Recall the distributive law of intersection (Fig.1.14 of section 1.6):
X ∩ (Y ∪ Z) = (X ∩ Y) ∪ (X ∩ Z)
2. Applying this law, the LHS becomes:
(A ∩ A) ∪ (A ∩ B)
3. But (A ∩ A) is A
• So the LHS becomes:
A ∪ (A ∩ B)
4. But in part (a), we proved that A ∪ (A ∩ B) is A.
• So the LHS becomes A.
5. Thus we get LHS = RHS
In
the next
section, we will see some relations between three sets.
Previous
Contents
Next
Copyright©2021 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment