Chapter 1.8 - Complement of a Set

In the previous section, we saw difference of sets. In this section, we will see complement of sets.

Complement of a set

• This can be explained in 9 steps:
1. Let U be a universal set which contains of all prime numbers.
• So U = {2, 3, 5, 7, 11, 13, . . .}
2. Let A be a set which contains all prime numbers which are not divisors of 42.
    ♦ Then A will be same as U, except for 2, 3 and 7
    ♦ This is because, 2, 3 and 7 are divisors of 42
        ✰ Prime numbers which are divisors of 42 are not allowed in A.
        ✰ Only the remaining prime numbers are allowed in A.
• So A = {5, 11, 13, . . .}
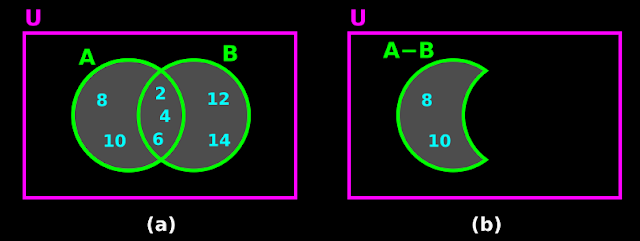
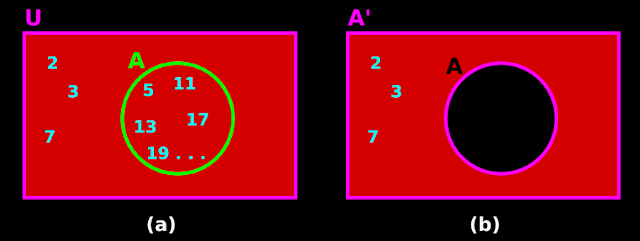
3. If we draw the Venn diagram, we will get fig.1.19(a) below:

Fig.1.19

• All elements except 2, 3 and 7 will lie inside the circle A.
• 2, 3 and 7 will lie outside the circle but inside the rectangle.
4. The set which contains those elements which lie outside the circle A, but inside the rectangle is called complement of A with respect to U.
    ♦ It is denoted by A’.
◼ So we can write: A’ = {2, 3, 7}
    ♦ Fig.b shows the Venn diagram of A’
• Note that, the portion of A is made hollow. This is because, we discard all elements of A.
5. It is clear that,
    ♦ All elements of A’ will be elements of U.
    ♦ Also, none of the elements of A’ will be an element of A.
6. We can write the definition:

Definition 9: The complement set A’ is that set which contains all elements of U, which are not elements of A

• Using symbols, we write: A’ = {x : x ∈ U and x ∉ A}
7. From the Venn diagram, it is clear that, A’ is obtained by removing A from U.
◼ So we can write: A’ = U－A
• In fig.1.19(b), the name of the rectangle is changed to A'. This is because, the rectangle no longer contains the elements of A. So it can no longer be called U. When A is removed, U becomes A'.
8. Let us see an example:
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {1, 3, 5, 7, 9}. Find A′.
Solution:
• We have: A' = U－A
• U － A can contain elements of U.
• U － A cannot contain any element of A.
    ♦ So we can right away discard set A.
• Also, U － A cannot contain any element which is common to both U and A.
   ♦ Thus we get: A' = U － A = {2, 4, 6, 8, 10}
9. Another example:
Let U = {x : x is a letter in the English alphabet} and A = {x : x is a vowel}. Find A'.
Solution:
• We have: A' = U－A
• U － A can contain elements of U.
• U － A cannot contain any element of A.
    ♦ So we can right away discard set A.
• Also, U － A cannot contain any element which is common to both U and A.
   ♦ So we remove all vowels from U.
   ♦ Thus we get: A' = U － A = {x : x is a consonant}.
10. Another example:
Let U = {x : x is a student in class XI} and A = {x : x is boy student in class XI}. Find A'.
Solution:
• We have: A' = U－A
• U － A can contain elements of U.
• U － A cannot contain any element of A.
    ♦ So we can right away discard set A.
• Also, U － A cannot contain any element which is common to both U and A.
   ♦ So we remove all boy students from U.
   ♦ Thus we get: A' = U － A = {x : x is a girl student in class XI}.
11. An interesting result can be derived in steps:
(i) Consider the example in (8). We derived the complement set A'.
(ii) Let us find the complement of this complement set.
• We have: (A')' = U － A'
(iii) That means, we have to remove all elements of A' from U.
• We get: (A')' = U － A' = {1, 3, 5, 7, 9}.
(iv) But {1, 3, 5, 7, 9} is A.
• So we can write: (A')' = A
12. Another example:
Let U = {1, 2, 3, 4, 5, 6}, A = {2, 3} and B = {3, 4, 5}.
Find A', B' , A' ∩ B', A ∪ B and hence show that (A ∪ B)' = A' ∩ B'.
solution:
(i) A' = U － A = {1, 4, 5, 6}
(ii) B' = U － B = {1, 2, 6}
(iii) A' ∩ B' = {1, 6}
(iv) A ∪ B = {2, 3, 4, 5}
(v) (A ∪ B)' = U － (A ∪ B) = {1,6}
(vi) From (iii) and (v), we see that: A' ∩ B' = (A ∪ B)'
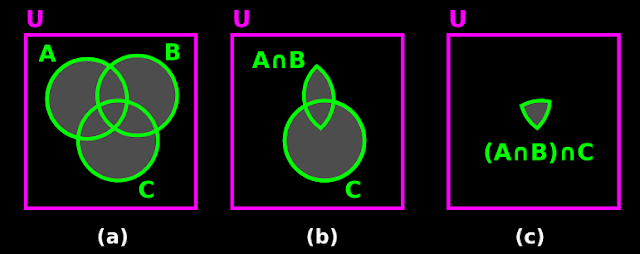
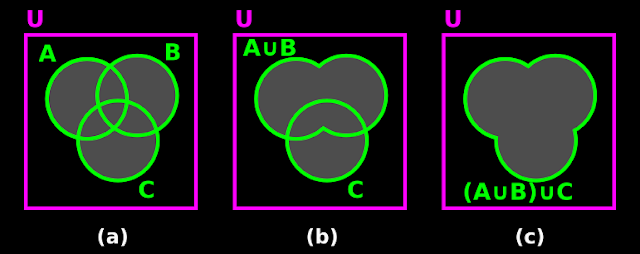
13. The result in 12(vi) above, can be used as a general formula. It can be proved using Venn diagrams. We can write it in 7 steps:
(i) Fig.1.20(a) below shows A and B before union.
   ♦ Fig.1.20(b) shows A ∪ B.
   ♦ Fig.1.20(c) shows (A ∪ B)'.

Fig.1.20

(ii) Venn diagrams for individual complement sets:
• Fig.1.21(a) below shows A'.
   ♦ The set B is not present in A'. So it is drawn using a dotted curve.
   ♦ It's presence is imaginary.
   ♦ It is shown only to give an idea about the 'position of B' relative to A.

Fig.1.21

• Fig.1.21(b) shows B'
   ♦ The set A is not present in B'. So it is drawn using a dotted curve.
   ♦ It's presence is imaginary.
   ♦ It is shown only to give an idea about the 'position of A' relative to B.
(iii) Now we want the final fig. to show A' ∩ B'
• For that, we superimpose fig.1.21(a) over 1.21(b)
• Only 'that region' where both the following two regions fall, is eligible to be designated as A' ∩ B'.
   ♦ The red region from fig.a
   ♦ And the red region from fig.b
(Recall that, for intersection, elements from both the sets should be present)
(iv) In fig.a, the circle A does not have red shading. So that portion will not have red shading in A' ∩ B'.
(v) In fig.b, the circle B does not have red shading. So that portion will not have red shading in A' ∩ B'.
(vi) Thus when fig.a is superimposed on fig.b, the result will be as in fig.c
• We can write: Fig.1.21(c) shows A' ∩ B'.
(vii) Now compare fig.1.20(c) and fig.1.21(c)
   ♦ We see that, both are same.
◼ So we can write: (A ∪ B)' = A' ∩ B'
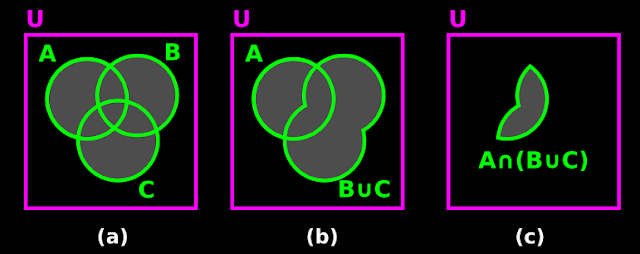
14. We can prove a similar result in 7 steps:
(i) Fig.1.22(a) below shows A and B before intersection.
   ♦ Fig.1.22(b) shows A ∩ B.
   ♦ Fig.1.22(c) shows (A ∩ B)'.

Fig,1.22

(ii) Venn diagrams for individual complement sets.
• Fig.1.23(a) below shows A'.
   ♦ The set B is not present in A'.
   ♦ So it is drawn using a dotted curve.It's presence is imaginary.
   ♦ It is shown only to give an idea about the position of B relative to A

Fig.1.23

• Fig.1.23(b) shows B'
   ♦ The set A is not present in B'.
   ♦ So it is drawn using a dotted curve. It's presence is imaginary.
   ♦ It is shown only to give an idea about the 'position of A' relative to B.
(iii) Now we want the final fig. to show A' ∪ B'.
• For that, we superimpose fig.1.23(a) over 1.23(b)
• 'That region' where any one of the following two regions fall, is eligible to be designated as A' ∪ B'.
   ♦ The red region from fig.a
   ♦ And the red region from fig.b
(Recall that, for union, elements from any one of the sets may be present)
(iv) In fig.a, the circle A does not have red shading. So it seems that, A will be absent in A' ∪ B'.
   ♦ But in the place of A, the dotted crescent is present in fig.b.
   ♦ It will compensate a major portion of A.
(v) In fig.b, the circle B does not have red shading. So it seems that, B will be absent in A' ∪ B'.
   ♦ But in the place of B, the dotted crescent is present in fig.a.
   ♦ It will compensate a major portion of B.
(vi) Thus when fig.a is superimposed on fig.b, the result will be as in fig.c
• We can write: Fig.1.23(c) shows A' ∪ B'.
(vii) Now compare fig.1.22(c) and fig.1.23(c)
   ♦ We see that, both are same.
◼ So we can write: (A ∩ B)' = A' ∪ B'
15. Let us write the two results together:
   ♦ From (13), we have: (A ∪ B)' = A' ∩ B'
   ♦ From (14), we have:  (A ∩ B)' = A' ∪ B'
• The first result states that:
The complement of the union of two sets is the intersection of their complements
   ♦ That means,
         ✰ Complement of a union
         ✰ is equal to
         ✰ intersection of the individual complements
• The second result states that:
The complement of the intersection of two sets is the union of their complements.
   ♦ That means,
         ✰ Complement of a intersection
         ✰ is equal to
         ✰ union of the individual complements
◼ The two results are together called De Morgan’s laws.

---

Some Properties of Complement Sets
1. Complement laws:
(i) A ∪ A′ = U 
• This is obvious from fig.1.19 that we saw at the beginning of this section.
• It is the union of two items:
   ♦ The set A' in fig.1.19(b).
   ♦ The set A in fig.1.19(a).
• The result will be U.
(ii) A ∩ A′ = ɸ
• This is obvious because, A' and A' will never have any common elements.
2. De Morgan’s law:
(i) (A ∪ B)' = A' ∩ B'
(ii) (A ∩ B)'′ = A' ∪ B'
• We have seen the proofs based on figs.1.20 to 1.23
3. Law of double complementation: (A')' = A
• We saw the proof in step (11) above.
4. Laws of empty set and universal set ɸ' = U and U' = ɸ

---

The link below gives some solved examples:

Solved examples 1.38 to 1.44

---

In the next section, we will see some practical problems.

Previous

Contents

Next

Copyright©2021 Higher secondary physics.blogspot.com

Chapter 1.7 - Difference of Sets

In the previous section, we saw intersection of sets. In this section, we will see difference of sets.

Difference of sets

• This can be explained in 9 steps:
1. Let A and B be any two sets.
• We perform an operation called ‘difference of sets’ between A and B.
2. The set which is formed as a result of that operation,
    ♦ will contain only those elements of A which do not belong to B.
• This can be explained further as follows:
    ♦ The resulting set can contain elements of A.
    ♦ The resulting set can not contain any element of B.
    ♦ The resulting set can not contain any element which is common to A and B.
3. The symbol ‘－’ is used to represent difference.
• So the difference of A and B can be represented as A － B.
    ♦ It is read as: A minus B.
4. Let us see some examples:
A = {2, 4, 6, 8, 10} and B = {2, 4, 6, 12, 14}. Find A － B.
Solution:
• A － B can contain elements of A.
• A － B can not contain any element of B.
    ♦ So we can right away discard set B.
• Also, A － B cannot contain any element which is common to both A and B.
    ♦ So we can discard 2, 4 and 6 from A.
• Thus we get: A － B = {8, 10}
• We can represent this difference using Venn diagrams also.
    ♦ Fig.1.16(a) below shows A and B before the difference.
    ♦ Fig.1.16(b) shows the new set which is A － B.

Fig.1.16

5. In the above example, find B － A
Solution:
• B － A can contain elements of B.
• B － A cannot contain any element of A.
    ♦ So we can right away discard set A.
• Also, B － A cannot contain any element which is common to both B and A.
    ♦ So we can discard 2, 4 and 6 from B.
• Thus we get: B － A = {12, 14}
• We can represent this difference using Venn diagrams also.
    ♦ Fig.1.17(a) below shows A and B before the difference.
    ♦ Fig.1.17(b) shows the new set which is B － A.

Fig.1.17

6. The above two examples show that:
    ♦ A － B
    ♦ is not equal to
    ♦ B － A
• So we must be careful about the order while specifying the difference.
• We must clearly examine the two sets:
    ♦ The set on the left side of '－' sign.
    ♦ The set on the right side of '－' sign.
7. Another example:
Let V = {a, e, i, o, u} and B = {a, i, k, u}. Show that V － B ≠ B － V 
Solution:
(i) V － B can contain elements of V.
• V － B cannot contain any element of B.
    ♦ So we can right away discard set B.
• Also, V － B cannot contain any element which is common to both V and B.
    ♦ So we can discard a, i and u from V.
• Thus we get: V － B = {e, o}
(ii) B － V can contain only elements of B.
• B － V cannot contain any element of V.
    ♦ So we can right away discard set V.
• Also, B － V cannot contain any element which is common to both V and B.
    ♦ So we can discard a, i and u from B.
• Thus we get: V － B = {k}
(iii) Thus we see that: V － B ≠ B － V
8. Thus we can write the definition:

Definition 8: The difference of two sets A and B is the set C which consists of all those elements which belong to A but not to B.

9. Let us see the relation between intersection and difference. It can be written in 4 steps:
(i) Consider two sets A and B.
• We can performs the operations of intersection and difference on the two sets.
(ii) As a result of those operations, we get three different sets:
A － B, B － A and A ∩ B
(Recall that, A ∩ B is same as B ∩ A. So the operation of intersection will give only one set)
(iii) Fig.1.18(a) below shows the two sets A and B before the operations.
• Fig.b shows the three resulting sets.

Fig.1.18

(iv) We see that, the three resulting sets do not have any overlapping parts.
◼ Thus we can write:
A － B, B － A and A ∩ B are mutually disjoint. They will never have any common elements.

Now we will see some solved examples:
Solved example 1.26
Find the union of each of the following pairs of sets :
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = [ a, e, i, o, u} B = {a, b, c}
(iii) A = {x : x is a natural number and multiple of 3}
B = {x : x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 < x ≤ 6 }
B = {x : x is a natural number and 6 < x < 10 }
(v) A = {1, 2, 3}, B = ɸ
Solution:
(i) X ∪ Y = {1, 2, 3, 5}
(ii) A ∪ B = {a, b, c, e, i, o, u}
(iii) In roster form, A = {3, 6, 9, 12, . . .}
• In roster form, B = {1, 2, 3, 4, 5}
• So A ∪ B = {x : x = 1, 2, 4, 5 or a multiple of 3}
(iv) In roster form, A = {2, 3, 4, 5, 6}
• In roster form, B = {7, 8, 9}
• So A ∪ B = {2, 3, 4, 5, 6, 7, 8, 9}
(v) A ∪ B = {1, 2, 3}

Solved example 1.27
Let A = { a, b }, B = {a, b, c}. Is A ⊂ B ? What is A ∪ B ?
Solution:
• All elements of A are present in B. So A ⊂ B
• A ∪ B = {a, b, c} = B

Solved example 1.28
If A and B are two sets such that A ⊂ B, then what is A ∪ B
Solution:
If A is a subset of B, then A ∪ B will be B

Solved example 1.29
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 } and D = { 7, 8, 9, 10 }; find
(i) A ∪ B  (ii) A ∪ C  (iii) B ∪ C  (iv) B ∪ D  (v) A ∪ B ∪ C  (vi) A ∪ B ∪ D  (vii) B ∪ C ∪ D
Solution:
(i) A ∪ B = {1, 2, 3, 4, 5, 6}
(ii) A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(iii) B ∪ C = {3, 4, 5, 6, 7, 8}
(iv) B ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}
(v) A ∪ B = {1, 2, 3, 4, 5, 6}
   ♦ So A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(vi) A ∪ B = {1, 2, 3, 4, 5, 6}
   ♦ So A ∪ B ∪ D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(vii) B ∪ C = {3, 4, 5, 6, 7, 8}
   ♦ So B ∪ C ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}

Solved example 1.30
Find the intersection of each pair of sets of example 1.26 above.
Solution:
(i) X ∩ Y = {1, 3}
(ii) A ∩ B = {a}
(iii) In roster form, A = {3, 6, 9, 12, . . .}
• In roster form, B = {1, 2, 3, 4, 5}
• So A ∩ B = {3}
(iv) In roster form, A = {2, 3, 4, 5, 6}
• In roster form, B = {7, 8, 9}
• So A ∩ B = ɸ
(v) A ∩ B = ɸ {1, 2, 3}

Solved example 1.31
If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}; find
(i) A ∩ B  (ii) B ∩ C  (iii) A ∩ C ∩ D  (iv) A ∩ C  (v) B ∩ D  (vi) A ∩ (B ∪ C) (vii) A ∩ D
(viii) A ∩ (B ∪ D)  (ix) ( A ∩ B ) ∩ ( B ∪ C )  (x) (A ∪ D) ∩ (B ∪ C)
Solution:
(i) A ∩ B = {7, 9, 11}
(ii) B ∩ C = {11, 13}
(iii) A ∩ C = {11}
   ♦ So A ∩ C ∩ D = ɸ
(iv) A ∩ C = {11}
(v) B ∩ D = ɸ
(vi) B ∪ C = {7, 9, 11, 13, 15}
   ♦ So A ∩ (B ∪ C) = {7, 9, 11}
(vii) A ∩ D = ɸ
(viii) B ∪ D = {7, 9, 11, 13, 15, 17}
   ♦ So A ∩ (B ∪ D) = {7, 9, 11}
(ix) A ∩ B = {7, 9, 11}
• B ∪ C = {7, 9, 11, 13, 15}
   ♦ So ( A ∩ B ) ∩ ( B ∪ C )   = {7, 9, 11}
(x) A ∪ D = {3, 5, 7, 9, 11, 15, 17}
• B ∪ C = {7, 9, 11, 13, 15}
   ♦ So ( A ∩ B ) ∩ ( B ∪ C ) = {7, 9, 11, 15}

---

The link below gives some solved examples:

Solved examples 1.32 to 1.37

---

In the next section, we will see complement of a set.

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 1.6 - Intersection of Sets

In the previous section, we saw Venn diagrams and union of sets. In this section, we will see intersection of sets.

Intersection of sets

• This can be explained in 9 steps:
1. Let A and B be any two sets.
• We perform an operation called ‘intersection of sets’ between A and B.
2. The set which is formed as a result of that operation,
    ♦ will contain only those elements which are common to both A and B.
3. The symbol ‘∩’ is used to represent intersection.
• So the intersection of A and B can be represented as A ∩ B.
5. Let us see some examples:
A = {2, 4, 6, 8, 10} and B = {2, 4, 6, 12, 14}. Find A ∩ B.
Solution:
• A ∩ B must contain only those elements which are common to both A and B.
• The elements 2, 4 and 6 are the only elements that appear in both A and B. So A ∩ B will contain only those elements.
• Thus we get: A ∩ B = {2, 4, 6}
• We can represent this intersection using Venn diagrams also.
    ♦ Fig.1.9(a) below shows A and B before the intersection.
    ♦ Fig.1.9(b) shows the new set which is A ∩ B.

Fig.1.9

 6. Another example:
Let A = { a, e, i, o, u } and B = { a, i, u }. Show that A ∩ B = B
Solution:
• A ∪ B must contain only those elements which are common to both A and B.
• The elements a, i and u are the only elements that appear in both A and B. So A ∩ B will contain only those elements.
• Thus we get: A ∩ B = {a, i, u}
    ♦ We see that, A ∩ B is same as B.
• We can represent this intersection using Venn diagrams also.
    ♦ Fig.1.10(a) below shows A and B before the intersection.
    ♦ Fig.1.10(b) shows the new set which is A ∩ B.

Fig.1.10

• We see that, all elements of B are contained in A. So B ⊂ A.
    ♦ When the intersection takes place, the resulting set is same as the subset.
    ♦ We can write: B ⊂ A ⇒ A ∩ B = B
◼  Compare this result with that of the union: B ⊂ A ⇒ A ∪ B = A.
• We see that:
   ♦ When there is union between superset and subset, the result is same as the superset.
   ♦ When there is intersection between superset and subset, the result is same as the subset.
7. One more example:
Let X = {Ram, Geeta, Akbar} be the set of students of Class XI, who are in school hockey team. Let Y = {Geeta, David, Ashok} be the set of students from Class XI who are in the school football team. Find X ∩ Y and interpret the set.
Solution:
• We have: X ∩ Y = {Geeta}
• We see that:
The set X ∩ Y consists of members who are both in the hockey team and football team.
8. Thus we can write the definition:

Definition 7: The intersection of two sets A and B is the set C which consists of all those elements which belong to both A and B.

• In symbols, we write: A ∩ B = { x : x ∈ A and x ∈ B }
◼  Compare this result with that of the union: A ∩ B = { x : x ∈ A or x ∈ B}
• We see that,
   ♦ In the case of union, we have 'or' between x ∈ A and x ∈ B.
   ♦ In the case of intersection, we have 'and' between x ∈ A and x ∈ B.
9. Consider two sets: A = {2, 4, 6, 8} and B = {1, 3, 5, 7}
• There are no elements which are common to both sets. So if we perform the operation of intersection, there will not be any elements in A ∩ B.
   ♦ That means, A ∩ B will be a null set.
• Any two sets which give a null set when intersection is performed, are called disjoint sets.
• We can write: If A ∩ B = ɸ, then A and B are disjoint sets.
• Disjoint sets can be represented using Venn diagrams as shown in fig.1.11 below: 

Fig.1.11

• We see that, disjoint sets do not overlap in Venn diagram.

---

Some Properties of the Operation of Intersection

1. A ∩ B = B ∩ A (Commutative law)
• This is obvious from fig.1.9 above.
    ♦ Both A ∩ B and B ∩ A will give the same result in fig.1.9(b).
2. (A ∩ B) ∩ C = A ∩ (B ∩ C) (Associative law).
• This can be proved in 3 steps, using Venn diagrams.
(i) Fig.1.12(a) below shows the three sets A, B and C.

Fig.1.12

• Fig.b shows (A ∩ B) and C.
    ♦ Fig.c shows the intersection between (A ∩ B) and C.
(ii) Fig.1.13(a) below shows the three sets A, B and C.

Fig.1.13

• Fig.b shows A and (B ∩ C).
    ♦ Fig.c shows the intersection between A and (B ∩ C).
(iii) We see that
    ♦ Fig.1.12(c)
    ♦ is same as
    ♦ Fig.1.13(c)
3. ɸ ∩ A = ɸ (Law of ɸ)
• This is obvious because,
    ♦ There are no elements common to ɸ and A.
4. U ∩ A = A (Law of U).
• This is obvious because,
    ♦ 'Elements of A' are the only elements which are common to both U and A.
5. A ∩ A = A (Idempotent law).
• This is obvious because,
    ♦ 'Elements of A' are the only elements which are common to both A and A.
(6) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)  (Distributive law)
• This can be proved using Venn diagrams.
(i) The left side of the '=' sign is shown in fig.1.14 below:

Fig.1.14

• Fig.1.14(a) shows the three sets A, B and C.
• Fig.b shows A and (B ∪ C).
    ♦ Fig.c shows the intersection between A and (B ∪ C).
(ii) The right side of the '=' sign is shown in fig.1.15 below:

Fig.1.15

• Fig.1.15(a) shows A ∩ B.
• Fig.b shows A ∩ C.
    ♦ Fig.c shows the union between (A ∩ B) and (A ∩ C).
(iii) We see that
    ♦ Fig.1.14(c)
    ♦ is same as
    ♦ Fig.1.15(c)

---

In the next section, we will see difference of sets

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 1.5 - Venn Diagrams

In the previous section, we saw power set and universal set. In this section, we will see Venn diagrams. Later in this section, we will also see union of sets.

• Basics of Venn diagrams can be explained in 3 steps:
1. In Venn diagrams, the universal set is represented by a rectangle.
    ♦ All other sets are represented by circles.
• We know that, all other sets will be subsets of U.
    ♦ So the circles are enclosed within the rectangle.
2. In fig.1.4(a) below,
    ♦ Set A = {2, 4, 6, 8, 10}
    ♦ Set B = {2, 4, 6, 12, 14}

Fig.1.4

• All elements of A and all elements of B belong to U.
• We see that, both A and B possess 2, 4 and 6.
• So we are inclined to think that, U possess two 2, two 4 and two 6
3. Recall that, in sets, repeating elements are written only once. This is applicable to universal set also.
• So the fig.a must be modified. The modified fig. is shown in fig.1.4(b)
• In the modified fig., we see that,
    ♦ The two circles over lap.
        ✰ But the circle A encloses all elements of set A.
        ✰ Also, the circle B encloses all elements of set B.
• Thus we get:
A = {2, 4, 6, 8, 10}
B = {2, 4, 6, 12, 14}
U = {2, 4, 6, 8, 10, 12, 14, 16, 18}

---

Operations on sets

• Consider the familiar operation of addition that we perform on two numbers say 5 and 12.
    ♦ As a result of the operation, we get a new number 17
• Subtraction is another operation that we perform on two numbers.
• We can perform certain operations on sets also.
    ♦ As a result of such an operation, we get a new set.
• We will now discuss about those operations that we perform between two sets.

Union of sets

• This can be explained in 8 steps:
1. Let A and B be any two sets.
• We perform an operation called ‘union of sets’ between A and B.
2. The set which is formed as a result of that operation,
    ♦ will contain all the elements of A.
    ♦ will contain all the elements of B.
3. But there is an important point to remember. It can be written in 3 steps:
(i) Some elements may be present in both the sets A and B.
(ii) So when we write the elements of A and B together, such elements will appear twice.
(iii) However, in the resultant set, those repeating elements should be written only once.
4. The symbol ‘∪’ is used to represent union.
• So the union of A and B can be represented as A ∪ B
5. Let us see some examples:
A = {2, 4, 6, 8, 10} and B = {2, 4, 6, 12, 14}. Find A ∪ B.
Solution:
• A ∪ B must contain all the elements of A and B.
• The elements 2, 4 and 6 appear in both A and B. They must be written only once in A ∪ B.
• Thus we get: A ∪ B = {2, 4, 6, 8, 10, 12, 14}
• We can represent this union using Venn diagrams also.
    ♦ Fig.1.5(a) below shows A and B before the union.
    ♦ Fig.1.5(b) shows the new set which is A ∪ B.

Fig.1.5

6. Another example:
Let A = { a, e, i, o, u } and B = { a, i, u }. Show that A ∪ B = A
Solution:
• A ∪ B must contain all the elements of A and B.
• The elements a, i and u appear in both A and B. They must be written only once in A ∪ B.
• Thus we get: A ∪ B = {a, e, i, o, u}
    ♦ We see that, A ∪ B is same as A.
• We can represent this union using Venn diagrams also.
    ♦ Fig.1.6(a) below shows A and B before the union.
    ♦ Fig.1.6(b) shows the new set which is A ∪ B

Fig.1.6

• We see that, all elements of B are contained in A. So B ⊂ A
    ♦ When the union takes place, the resulting set is same as the superset
    ♦ We can write: B ⊂ A ⇒ A ∪ B = A
7. One more example:
Let X = {Ram, Geeta, Akbar} be the set of students of Class XI, who are in school hockey team. Let Y = {Geeta, David, Ashok} be the set of students from Class XI who are in the school football team. Find X ∪ Y and interpret the set.
Solution:
• We have: X ∪ Y = {Ram, Geeta, Akbar, David, Ashok}
• We see that:
The set X ∪ Y consists of members who are in the hockey team or football team or both
8. Thus we can write the definition:

Definition 6: The union of two sets A and B is the set C which consists of all those elements which are either in A or in B (including those which are in both).

• In symbols, we write: A ∪ B = { x : x ∈ A or x ∈ B }

---

Some Properties of the Operation of Union

1. A ∪ B = B ∪ A (Commutative law)
• This is obvious from fig.1.5 above.
    ♦ Both A ∪ B and B ∪ A will give the same result in fig.1.5(b)
2. (A ∪ B) ∪ C = A ∪ (B ∪ C) (Associative law)
• This can be proved in 3 steps, using Venn diagrams.
(i) Fig.1.7(a) below shows the three sets A, B and C.

Fig.1.7

• Fig.b shows (A ∪ B) and C.
    ♦ Fig.c shows the union between (A ∪ B) and C.
(ii) Fig.1.8(a) below shows the three sets A, B and C.

Fig.1.8

• Fig.b shows A and (B ∪ C).
    ♦ Fig.c shows the union between A and (B ∪ C).
(iii) We see that
    ♦ Fig.1.7(c)
    ♦ is same as
    ♦ Fig.1.8(c)
3. A ∪ ɸ = A (Law of identity element, ɸ is the identity of ∪)
• This is obvious because,
    ♦ A ∪ ɸ must contain all elements of A and ɸ.
    ♦ That means, A ∪ ɸ will contain only the elements of A.
4. A ∪ A = A (Idempotent law)
• This is obvious because,
    ♦ A ∪ A must contain all elements of A and A.
    ♦ But we know that, repeating elements are written only once.
    ♦ That means, A ∪ A will contain only the elements of A.
(5) U ∪ A = U (Law of U)
• This is obvious because,
    ♦ U ∪ A must contain all elements of U and A.
    ♦ U already contains A.
    ♦ But we know that, repeating elements are written only once.
    ♦ That means, U ∪ A will be same as U.

---

In the next section, we will see intersection of sets

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 1.4 - Power Set and Universal Set

In the previous section, we saw the basics about subsets. In this section, we will see the subsets of R. Later in this section, we will also see intervals, power sets and the universal set.

• In the first section of this chapter, we saw the details about sets like N, Z, Q, T, R etc., (Details here).
• Based on that, we can write about the subsets of R. It can be written in 4 steps:
1. We can plot all elements of Z on the number line.
• When we make such a plot, all the elements of N will also be present among those Z values.
◼ Consider the reverse:
• We can plot all elements of N on the number line
• When we make such a plot, all the elements of Z will not be present among those N values.
◼ So we can write:
    ♦ All elements of N are present in Z.
    ♦ All elements of Z are not present in N.
• Thus we get: N ⊂ Z and Z ⊄ N
2. We can plot all elements of Q on the number line.
• When we make such a plot, all the elements of Z will also be present among those Q values.
◼ Consider the reverse:
• We can plot all elements of Z on the number line.
• When we make such a plot, all the elements of Q will not be present among those Z values.
◼ So we can write:
    ♦ All elements of Z are present in Q.
    ♦ All elements of Q are not present in Z.
• Thus we get: Z ⊂ Q and Q ⊄ Z
• But in (1), we saw that, N ⊂ Z
    ♦ So we can write: N ⊂ Z ⊂ Q
• That means, when we plot Q, all elements of N and Z will also be present among those Q values.
3. We can plot all elements of R on the number line.
• When we make such a plot, all the elements of Q will also be present among those R values.
◼ Consider the reverse:
• We can plot all elements of Q on the number line.
• When we make such a plot, all the elements of R will not be present among those Q values.
◼ So we can write:
    ♦ All elements of Q are present in R.
    ♦ All elements of R are not present in Q.
• Thus we get: Q ⊂ R and R ⊄ Q
• But in (2), we saw that, Z ⊂ Q
    ♦ So we can write: Z ⊂ Q ⊂ R
• Also in (1), we saw that, N ⊂ Z
    ♦ So we can write: N ⊂ Z ⊂ Q ⊂ R
• That means, when we plot R, all elements of N, Z and Q will also be present among those R values.
4. We know the reason why Q does not contain all the elements of R
• Let us write it:
Set R contains both rational numbers and irrational numbers (T). But Q does not contain irrational numbers

---

Intervals as subsets of R

This can be explained in 9 steps:
1. Let a and b be two real numbers, with b being greater than a.
    ♦ a will have a unique position on the number line.
    ♦ b will also have a unique position on the number line.
• Those positions are shown in fig.1.3(i) below:

Fig.1.3

2. There will be infinite number of points between a and b.
• The portion between a and b is a continuous portion. There are no breaks between a and b.
• So we can say:
The portion between a and b is an interval between a and b in the number line.
3. We can define a set which contains all the points in that interval.
• The points in that set must satisfy two conditions:
(i) The points must lie to the right of a.
(ii) The points must lie to the left of b.
◼ This set can be written in set-builder form as: {y : a < y < b}
That means, y is greater than a and at the same time, less than b.
4. Whether to include a and b in the set:
• y must be greater than a.
    ♦ So a is not included.
• y must be less than b.
    ♦ So b is not included.
◼ That means, a and b, which defines the boundaries of the interval, are not included in the set.
◼ So it is called an open interval.
• It is denoted as (a, b).
5. If we include the boundaries also, then it is called a closed interval.
    ♦ It is denoted as [a, b].
• In set-builder form, it will be: {y : a ≤ y ≤ b}
    ♦ It is shown in fig.1.3(ii) above.
    ♦ Both a and b will be present in the set.
6. We can also have intervals which are closed at one end and open at the other.
• (a, b] is open at a and closed at b.
    ♦ In set-builder form, it will be: {y : a < y ≤ b}
    ♦ It is shown in fig.1.3(iii) above.
    ♦ a will not be present in the set but b will be present.
• [a, b) is closed at a and open at b.
    ♦ In set-builder form, it will be: {y : a ≤ y < b}
    ♦ It is shown in fig.1.3(iv) above.
    ♦ a will be present in the set but b will not be present.
7. Let us see an example:
• Consider the set: A = {x : x ∈ R, -3 ≤ x ≤ 5}
    ♦ This can be written in short form as: A = [-3, 5]
• Consider another set: B = {x : x ∈ R, -7 ≤ x ≤ 9}
    ♦ This can be written in short form as: B = [-7, 9]
• It is easy to visualize the number line containing the four points -3, 5, -7 and 9
    ♦ Obviously, the points -3 and 5 will lie within -7 and 9
• So all the infinite number of points from -3 to 5 will be present inside the set B
    ♦ Thus we get: A ⊂ B
8. Subsets of R:
• The infinite number of positive real numbers that we use in mathematics are members of the set: [0, ∞)
    ♦ This [0, ∞) is a subset of R
• The infinite number of negative real numbers that we use in mathematics are members of the set: (-∞, 0]
    ♦ This (-∞, 0] is a subset of R
• R can be represented as: (-∞, ∞)
9. The number (b - a) is called length of the interval [a, b]
• For the interval (a, b] also, the length is (b - a)
• This is because, even if we do not include a in the set, the length will begin from a point very close to a
• So in general, we can write:
(b - a) is the length of all the four intervals: [a, b], (a,b), (a, b] and [a, b)

---

Power Set

The power set can be explained using an example. It can be written in 9 steps:
1. Consider the set A = {1, 2}
• Let us write all the subsets of A.
2. We know that ɸ is a subset of every set.
• So ɸ is a subset of A.
3. {1} and {2} are subsets of A.
4. We know that, every set is a subset of itself.
• So in total, there are four subsets for A. They are:
ɸ, {1}, {2} and {1,2}
5. The set containing all those subsets is known as the power set of A.
We can write the definition:

Definition 5: • The set containing all subsets of a set A is called power set of A.     ♦ It is denoted as: p(A).

6. In p(A), every element is a set.
• So in the present case, we can write: p(A) = {ɸ, {1}, {2}, {1,2}}
7. Recall that, number of elements in a set is denoted as n(A).
    ♦ So in our present case, we get n(A) = 2
8. In the same way, we will need to write the number of elements in p(A) also.
• The number of elements in a power set is denoted using square brackets.
• So in our present case, the number of elements in p(A) is denoted as n[p(A)].
    ♦ Obviously, n[p(A)] = 4
9. For any set A, the number n[p(A)] will be equal to 2^m
    ♦ Where m = n(A)
◼ In other words,
    ♦ The number of elements in the power set of A is obtained by raising ‘2’ to a suitable number.
    ♦ This ‘suitable number’ is: The number of elements in A.

---

Universal Set

• This can be explained as follows:
• While doing problems in set theory, we will be dealing with:
   ♦ One basic set.
         ✰ Subsets of the basic set.
• For example, while dealing with simple numbers,
   ♦ The basic set may be Z.
         ✰ One subset may be even numbers.
         ✰ Another subset may be prime numbers.
• For more complex problems,
   ♦ The basic set may be R.
         ✰ One subset may be Q.
         ✰ Another subset may be T.
◼ Such a basic set (to which, all other sets are subsets) is called Universal set.

---

We will now see some solved examples. Link is given below:

Solved examples 1.20 to 1.25

---

In the next section, we will see Venn diagrams

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 1.3 - Subsets

In the previous section, we saw the empty set, finite set and equal sets. In this section, we will see subsets

Some basics about subsets can be written in 14 steps:
1. Consider the following two sets:
X = {x : x is a student in the school}
Y = {y : y is a student in class 11}
2. It is clear that, all elements in Y will be present in X.
• We say that: Y is a subset of X.
   ♦ Using symbols, this is written as: Y ⊂ X
   ♦ The symbol ‘⊂’ stands for ‘is a subset of’ or ‘is contained in’.
3. We can write the definition:

Definition 4 A set A is said to be a subset of set B if every element of A is contained in B.

4. We already know that:
If a is an element of A, we can write a ∈ A.
• But since A is a subset of B, the element a will be present in B also. So we can write: a ∈ B
5. That means,
If a ∈ A implies a ∈ B then, A ⊂ B.
• The word implies can be replaced by the symbol ‘⇒ ’. So we can write:
If a ∈ A ⇒ a ∈ B then, A ⊂ B.
6. There are two situations where A can be a subset of B
(i) Every element in A is present in B. Further, B has some extra elements also.
(ii) Every element in A is present in B. There are no extra elements in B.
   ♦ This means B has the exact same elements as A.
7. Let us consider the second situation carefully:
• If B has the exact same elements as A, we can write A ⊂ B alright.
   ♦ But we can write B ⊂ A also.
• That means, if two sets A and B have the exact same elements, we can write both:
A ⊂ B and B ⊂ A.
8. Recall that, if two sets have the exact same elements, they are equal sets.
• So we can write:
If A ⊂ B and B ⊂ A, the sets A and B are equal.
• Using symbols, we can write:
A ⊂ B and B ⊂ A ⇒ A = B
9. Conversely, we can write:
If two sets A and B are equal, then A ⊂ B and B ⊂ C.
10. A theorem and it’s converse can be written using the symbol ‘⇔’.
• This symbol indicates two way implication. So we get: A ⊂ B and B ⊂ A ⇔ A = B
   ♦ The forward direction indicates what we wrote in (8).
   ♦ The reverse direction indicates what we wrote in (9).
11. What we saw in steps (7) to (10) is the analysis of the situation in 6(ii).
• What if the situation is as in 6(i) ?
   ♦ In such a situation, we say two things:
         ✰ A is a proper subset of B.
         ✰ B is a superset of A.
12. Let us see some examples:
Example 1:
• Consider the following two sets:
A = {x : x is a divisor of 56}
B = {x : x is prime divisor of 56}
• Obviously, all elements in B will be present in A.
   ♦ So we can write: B ⊂ A
Example 2:
• Consider the following two sets:
A = {1, 3, 5}
B = {x : x is an odd number less than 6}
• The set B in roster form is {1, 3, 5}.
• So we can write:
   ♦ All elements of A are present in B.
         ✰ So A ⊂ B
   ♦ All elements of B are present in A.
         ✰ So B ⊂ A
• Since A ⊂ B and B ⊂ A, we can write A = B.
Example 3:
• Consider the following two sets:
A = {a, l, o, y}
B = {a, e, i, o, u}
• We see that, A is not a subset of B.
   ♦ We write: A ⊄ B
• We see that, B is not a subset of A.
   ♦ We write: B ⊄ A
13. From the above steps, it is clear that, every set A is a subset of itself
• Also, since the empty set ɸ has no elements, ɸ is a subset of every set
14. If a set A has only one element, we call it a singleton set
• For example, {a} is a singleton set

Solved example 1.18
Consider the sets
ɸ, A = { 1, 3 }, B = {1, 5, 9}, C = {1, 3, 5, 7, 9}.
Insert the symbol ⊂ or ⊄ between each of the following pair of sets:
(i) ɸ . . . B  (ii) A . . . B  (iii) A . . . C  (iv) B . . . C
Solution:
(i) Since is a subset of every set, we can write: ɸ ⊂ B
(ii) 3 is not present in B. So we write: A ⊄ B
(iii) Both 1 and 3 are present in C. So we write: A ⊂ C
(iv) All three elements 1, 5 and 9 are present in C. So we write B ⊂ C

Solved example 1.19
Let A, B and C be three sets. If A ∈ B and B ⊂ C, is it true that A ⊂ C?. If not, give an example.
Solution:
1. Let A = {1, 2}
• Given that, set A is an element of B. So we can write: B = {3, {1, 2}, 4}
• Given that B is a subset of C. So we can write: C = {3, {1, 2}, 4, 5}
2. Here we are inclined to think that, A is a subset of C
• But if we write a subset of C, it will be: {{1, 2}}
   ♦ {{1, 2}} is different from {1, 2}
   ♦ That is: {{1, 2}} is different from A.
• So the answer is: No, A cannot be a subset of C.
3. Another way to analyze this situation can be written in 3 steps:
(i) If A is to be a subset of C, all elements of A should be present in C as separate elements.
(ii) But in C, the elements 1 and 2 are present together as a set. Not as separate elements.
(iii) So the answer is: No, A cannot be a subset of C.

---

In the next section, we will see subsets of the set R

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 1.2 - Empty, Finite and Equal Sets

In the previous section, we saw the roster form and set-builder form. In this section, we will see empty set, finite set and equal sets.

The empty set can be described in 6 steps:
1. Consider the set:
A = {x : x is a student of Class XI presently studying in a school}
• Let us analyze this set:
We can write the names of all students of Class XI in that school. So set A will contain a definite number of names.
2.Consider another set:
B = {x : x is a student of both Class X and Class XI presently studying in that school}
• Let us analyze this set:
We will not find any student who studies in both Class X and Class XI in the same school. So set B will not contain any element.

Definition 1: • A set which does not contain any element is called the empty set    ♦ Another name for empty set is null set    ♦ Yet another name for empty set is void set

3. In our present case,
   ♦ A is not an empty set.
   ♦ B is an empty set.
4. Representing empty set:  
   ♦ Empty set is denoted by the symbol { }
   ♦ Another symbol for empty set is Ø
5. In our present case, we can write:
   ♦ A ≠ { }
   ♦ B = { }
6. Let us see a few more examples:
(i) Let A = {x : 1 < x < 2, x is a natural number}.
• Here x should be a natural number. Also, it must lie between 1 and 2.
• There is no such natural number. So the set will not contain any elements.
• In other words, A is an empty set.

(ii) B = {x : x² – 2 = 0 and x is rational number}.
• Here, the only solution of (x² – 2 = 0) is +√2 and -√2
• Both +√2 and -√2 are irrational numbers. So B is an empty set.

(iii) C = {x : x is an even prime number greater than 2}.
• Here, x should be:
    ♦ A prime number.
    ♦ An even number.
    ♦ Greater than 2.
• All prime numbers greater than 2 are odd numbers. So C is an empty set.

(iv) D = { x : x² = 4, x is odd}.
Here, the only solution of (x² = 4) is +2 and -2
• Both +2 and -2 are even numbers. So D is an empty set.

Solved example 1.10
Which of the following are examples of the null set
(i) Set of odd natural numbers divisible by 2
(ii) Set of even prime numbers
(iii) { x : x is a natural numbers, x < 5 and x > 7}
(iv) { y : y is a point common to any two parallel lines}
Solution:
(i) None of the odd natural numbers are divisible by 2
• So it is a null set.
(ii) All prime numbers except 2 are odd numbers.
• That means, there is one even prime number, which is '2'. So this is not a null set.
(iii) No natural number can be less than 5 and greater than 7 at the same time. So it is a null set.
(iv) Two parallel lines will never have a common point. So it is a null set.

---

Finite and Infinite sets

This can be explained in 7 steps
1. Consider the following set:
A = {2, 4, 6, 8}
• This set A has four elements. We write: n(A) = 4
   ♦ 4 is a finite natural number.
   ♦ So n(A) is a finite natural number.
2. Consider the following set:
V = {a, e, i, o, u}
• This set V has five elements. We write: n(V) = 5
   ♦ 5 is a finite natural number.
   ♦ So n(V) is a finite natural number.
3. Consider the following set:
C = {x : x is a citizen of India}
• This set will contain the names of all citizen of India. The elements are names.
   ♦ The ‘number of elements’ will be very large. But it will be a finite natural number.
   ♦ That is., n(C) will be a very large but finite natural number.
4. Consider the following set:
D = {x : x is a positive even number}
• This set will contain the numbers 2, 4, 6, 8, . . . The elements are even numbers.
   ♦ The ‘number of elements’ will be very very large.
   ♦ We will not be able to count them.
   ♦ That is., n(D) will be infinite.
5. We can now write the definition

Definition 2 • The set A is said to be a finite set if n(A) is a finite number.    ♦ The set A is said to be a finite set even if it is an empty set. • The set A is said to be an infinite set if n(A) is not a finite number.

6. Let us see some more examples:
(i) Consider the set:
D = {x : x is a day of the week}
• Then D = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
• We get: n(D) = 7
   ♦ '7' is a finite natural number. So D is a finite set.
(ii) Consider the set:
S = {x : x² – 16 = 0}.
• Here, x can take two values only. They are 4 and -4. So S = {4, -4}
• We get: n(S) = 2
   ♦ '2' is a finite natural number. So S is a finite set.
(iii) Consider the set:
G = {x : x is a point on a line}.
• There will be infinite number of points on a line.
• So G will contain infinite number of elements.
   ♦ That means, n(G) is not a finite number.
   ♦ So G is an infinite set.
7. We know that, in roster form, we write all the elements and enclose them within braces.
• But if the set is an infinite set, we will not be able to write all the elements.
• If the set is infinite, we write a few elements followed by three dots.
• Those few elements that are written, should clearly indicate the structure of the set.
• For example,
   ♦ If we write {1, 3, 5, 9, . . .}, it clearly indicates odd numbers.
   ♦ If we write {2, 2², 2³, 2⁴, . . .}, it clearly indicates the powers of 2.
• Some times, the three dots may precede the elements.
• For example,
   ♦ If we write { . . . , -3, -2, -1, 0, 1, 2, 3, . . .}, it clearly indicates integers.
◼ This method of providing three dots, cannot be used to indicate real numbers. This is because, real numbers do not follow any particular pattern. For example, the distance (on the number line) between √2 and √3 is not the same as that between √3 and √4.

Solved example 1.11
Which of the following sets are finite or infinite
(i) The set of months of a year
(ii) {1, 2, 3, . . .}
(iii) {1, 2, 3, . . .99, 100}
(iv) The set of positive integers greater than 100
(v) The set of prime numbers less than 99
Solution:
(i) The set will contain the names of the 12 months. The number of elements is 12. So it is a finite set.
(ii) This set has the definite pattern of natural numbers. But the pattern is followed by 3 dots. The dots indicate that, all the natural numbers must be included in the set. So it is an infinite set.
(iii) This set has the definite pattern of natural numbers. The pattern is followed by 3 dots. The dots usually indicate that, the set is infinite. But here, the last two elements are also given. It is clear that, there will be exactly 100 elements in the set. So it is a finite set.
(iv) There are infinite number of positive integers which are greater than 100. So it is an infinite set.
(v) There is a finite number of prime numbers which are less than 99. So it is a finite set.

Solved example 1.12
State whether each of the following set is finite or infinite:
(i) The set of lines which are parallel to the x-axis
(ii) The set of letters in the English alphabet
(iii) The set of numbers which are multiple of 5
(iv) The set of animals living on the earth
(v) The set of circles passing through the origin (0,0)
Solution:
(i) There are infinite number of lines which are parallel to the x-axis. So it is an infinite set.
(ii) There is a finite number of letters in the English alphabet. So it is a finite set.
(iii) There are infinite numbers which are multiple of 5. So it is an infinite set.
(iv) There is a finite number of animals living on the earth. So it is a finite set.
(iii) There are infinite number of circles passing through the origin (0,0). So it is an infinite set.

---

Equal Sets

This can be explained in 5 steps:
1. Suppose that, we have two sets A and B. We will be able to say that the two sets are equal, if two conditions are satisfied:
(i) All elements in A are present in B.
(ii) All elements in B are present in A.
2. But if the above two conditions are satisfied, it is obvious that, the two sets will be having the same elements.
3. So we can write the definition:

Definition 3 • Two sets A and B are said to be equal if they have exactly the same elements.    ♦ The equality is expressed as A = B • Two sets A and B are said to be unequal if they do not have exactly the same elements.    ♦ The inequality is expressed as A ≠ B

4. Let us see some examples:
Example (i):
• Let A = {2, 2¹⁄₂, 3, 3¹⁄₂} and B = {2, 3, 2¹⁄₂, 3¹⁄₂}
• We see that,
   ♦ All elements in A are present in B.
   ♦ All elements in B are present in A.
• A and B have exactly the same elements. They are equal sets.
   ♦ We write: A = B

Example (ii):
• Consider the following set:
A = {x : x is a prime number less than 6}
• Consider another set:
B = {x : x prime factor of 30}
• In roster form, the above sets are: A = {2, 3, 5} and B = {2, 3, 5}
We see that,
   ♦ All elements in A are present in B.
   ♦ All elements in B are present in A.
• A and B have exactly the same elements. They are equal sets.
   ♦ We write: A = B
5. An interesting note:
• Consider the sets: A = {1, 2, 3} and B= {2, 2, 1, 3, 3}
• We see that:
   ♦ All elements in A are present in B.
   ♦ All elements in B are present in A.
   ♦ So A = B
◼ That means, it not necessary to write the repeating elements in B more than once. That is the reason why in general, we avoid writing repeating elements more than once.

Solved example 1.13
Find the pairs of equal sets, if any, give reasons:
A = {0},
B = {x : x > 15 and x < 5},
C = {x : x – 5 = 0 },
D = {x: x² = 25},
E = {x : x is an integral positive root of the equation x² – 2x –15 = 0}.
Solution:
1. Let us convert those last 5 sets which are in set-builder form into roster form:
• We have: B = {x : x > 15 and x < 5}
   ♦ Obviously, no number can be less than 5 and greater than 15 at the same time.
   ♦ It is a null set.
   ♦ We can write: B = {}
• We have: C = {x : x – 5 = 0 }
   ♦ We can write: C = {5}
• We have: D = {x: x² = 25}
   ♦ Solving (x² = 25), we can write: D = {5, -5}
• We have: E = {x : x is an integral positive root of the equation x² – 2x –15 = 0}
   ♦ Solving (x² – 2x –15 = 0), the solution is 5 and -3
   ♦ But the set must contain only integral positive roots
   ♦ So we can write: E = {5}
2. So the sets are:
A = {0}, B = {}, C = {5}, D = {5, -5} and E = {5}
3. Let us compare each set with the others
(i) Set A:
• The element '0' is not present in any other set. So we write:
A ≠ B, A ≠ C, A ≠ D, A ≠ E
(ii) Set B:
• None of the other sets is a null set. So we write:
B ≠ A, B ≠ C, B ≠ D, B ≠ E
(iii) Set C:
• The element '5' is present only in E. The other sets cannot be equal to C. So we write:
C ≠ A, C ≠ B, C ≠ D
• Since '5' is present in 'E', we must check further. We see that, E has only '5'
• So we can write:
   ♦ All elements in C are present in E
   ♦ All elements in E are present in C
   ♦ Thus we get: C = E
(iv) Set D:
• D has '5' and '-5'. No other sets have both these elements. So we write:
D ≠ A, D ≠ B, A ≠ C, D ≠ E
(v) Set E
   ♦ We have already seen that, A, B and D are not equal to E
   ♦ We have also seen that, C = E
(vi) So the only equal pair is: C and E

Solved example 1.14
Which of the following pairs of sets are equal ? Justify your answer.
(i) X, the set of letters in “ALLOY” and B, the set of letters in “LOYAL”.
(ii) A = {n : n ∈ Z and n 2 ≤ 4} and B = {x : x ∈ R and x 2 – 3x + 2 = 0}.
Solution:
(i) We have: X = {A, L, O, Y} and B = {L, O, Y, A}.
   ♦ All elements in X are present in B
   ♦ All elements in B are present in X
• So we write: X = B
(ii) We have: A = {–2, –1, 0, 1, 2} and B = {1, 2}.
• We see that, '0' is present only in A
   ♦ All elements in A are not present in B
   ♦ All elements in B are present in A
• Since both conditions are not satisfied, we can write: A ≠ B

Solved example 1.15
In the following, state whether A = B or not:
(i) A = { a, b, c, d }, B = { d, c, b, a }
(ii) A = { 4, 8, 12, 16 }, B = { 8, 4, 16, 18}
(iii) A = {2, 4, 6, 8, 10}, B = { x : x is positive even integer and x ≤ 10}
(iv) A = { x : x is a multiple of 10}, B = { 10, 15, 20, 25, 30, . . . }
Solution:
(i) A = { a, b, c, d }, B = { d, c, b, a }
   ♦ All elements in A are present in B
   ♦ All elements in B are present in A
• So we write: A = B
(ii) A = { 4, 8, 12, 16 }, B = { 8, 4, 16, 18}
   ♦ All elements in A are not present in B
   ♦ All elements in B are not present in A
• So we write: A ≠ B
(iii) A = {2, 4, 6, 8, 10}, B = { x : x is positive even integer and x ≤ 10}
• Set B in roster form is: {2, 4, 6, 8, 10}
   ♦ All elements in A are present in B
   ♦ All elements in B are present in A
• So we write: A = B
(iv) A = { x : x is a multiple of 10}, B = { 10, 15, 20, 25, 30, . . . }
• Set A in roster form is: {10, 20, 30, 40, . . .}
   ♦ All elements in A are present in B
   ♦ All elements in B are not present in A
• So we write: A ≠ B

Solved example 1.16
Are the following pair of sets equal ? Give reasons.
(i) A = {2, 3}, B = {x : x is solution of x2 + 5x + 6 = 0}
(ii) A = { x : x is a letter in the word FOLLOW}, B = { y : y is a letter in the word WOLF}
Solution:
(i) A = {2, 3}, B = {x : x is solution of x² + 5x + 6 = 0}
• Set B in roster form is: {-2, -3}
   ♦ All elements in A are not present in B
   ♦ All elements in B are not present in A
• So we write: A ≠ B
(ii) A = { x : x is a letter in the word FOLLOW}, B = { y : y is a letter in the word WOLF}
• Set A in roster form is: {F, O, L, W}
• Set B in roster form is: {W, O, L, F}
   ♦ All elements in A are present in B
   ♦ All elements in B are present in A
• So we write: A = B

Solved example 1.17
From the sets given below, select equal sets :
A = { 2, 4, 8, 12}, B = { 1, 2, 3, 4}, C = { 4, 8, 12, 14}, D = { 3, 1, 4, 2},
E = {–1, 1}, F = { 0, a}, G = {1, –1}, H = { 0, 1}
Solution:
(i) Consider set A
• Take the first element '2'
   ♦ C, E, F, G and H can be ruled out because, '2' is not present in them
   ♦ The remaining sets are B and D
• Take the second element '4'
   ♦ This element is present in B and D
• Take the third element 8
   ♦ B and D can be ruled out because, '8' is not present in them
• So A is not equal to any other set

(ii) Consider set B
• Take the first element '1'
   ♦ A, C and F can be ruled out because, '1' is not present in them
   ♦ The remaining sets are D, E, G and H
• Take the second element '2'
   ♦ E, G and H can be ruled out because, '2' is not present in them
   ♦ The remaining set is D
• Take the third element '3'
   ♦ This element is present in D
• Take the fourth element '4'
   ♦ This element is present in D
   ♦ All the elements in B are present in D
• Comparing B and D, we see that:
   ♦ All the elements in B are present in D
   ♦ All the elements in D are present in B
◼ So B and D are equal sets

(iii) Consider set C
• A and B can be ruled out because, we already compared them with C
• Take the first element '4'
   ♦ E, F, G and H can be ruled out because, '4' is not present in them
   ♦ The remaining set is D
• Take the second element '8'
   ♦ D can be ruled out because, '8' is not present in it
• So C is not equal to any other set

(iv) Consider set D
• We already saw that,
   ♦ D = B
   ♦ B is not equal to any other set
• So D cannot be equal to any set other than B

(v) Consider set E
• A, B, C and D can be ruled out because, we already compared them with E
• Take the first element '-1'
   ♦ F and H can be ruled out because, '-1' is not present in them
   ♦ The remaining set is G
• Take the second element '1'
   ♦ This element is present in G
   ♦ All the elements in E are present in G
• Comparing E and G, we see that:
   ♦ All the elements in E are present in G
   ♦ All the elements in G are present in E
◼  So E and G are equal sets

(vi) Consider set F
• A, B, C, D and E can be ruled out because, we already compared them with F
• Take the second element 'a'
   ♦ G and H can be ruled out because, 'A' is not present in them
   ♦ There are no remaining sets to compare with F
• So F is not equal to any other set

(vii) Consider set G
• We already saw that,
   ♦ E = G
   ♦ E is not equal to any other set
• So G cannot be equal to any set other than E

(viii) Consider set H
• All other sets can be ruled out because, we already compared them with H
• So H is not equal to any other set

◼  Thus we get the final answer:
• The equal sets are:
   ♦ From (ii): B = D
   ♦ From (v): E = G

---

In the next section, we will see subsets

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com

Chapter 1.1 - Roster Form And Set-Builder Form

In the previous section, we saw an introduction to sets. In this section, we will see the two methods for representing a set.

◼ There are two methods for representing a set.
    ♦ Roster form
        ✰ This is also known as Tabular form.
    ♦ Set-builder form

We will first see roster form. Some basic features can be written in 5 steps:
1. In roster form, all elements of the set are clearly written.
2. The elements are separated by commas.
3. The elements are enclosed within braces.
4. The order in which the elements are written is not important.
5. Repeating elements are written only once.

Let us see some examples:
(a) Consider the following set:
• The set of all even positive integers which are less than 7.
    ♦ Clearly, the elements are 2, 4, and 6.
    ♦ We must clearly write all those three elements.
    ♦ We must separate them with commas.
    ♦ We must enclose them within braces.
• So the set will appear as: {2, 4, 6}
• If we decide to name the set as A, we can write: A = {2, 4, 6}
• Since the order is not important, we can write A = {4, 6, 2} also. Different arrangements like this are allowed.

(b) Consider the following set:
• The set of all natural numbers which completely divide 42
    ♦ Clearly, the elements are 1, 2, 3, 6, 7, 14, 21, and 42
    ♦ We must clearly write all those 8 elements.
    ♦ We must separate them with commas.
    ♦ We must enclose them within braces.
• So the set will appear as: {1, 2, 3, 6, 7, 14, 21, 42}
• If we decide to name the set as B, we can write: B = {1, 2, 3, 6, 7, 14, 21, 42}
• Since the order is not important, we can write B = {21, 42, 7, 14, 3, 6, 1, 2} also. Different arrangements like this are allowed.

(c) Consider the following set:
• The set of all vowels in English alphabet.
    ♦ Clearly, the elements are a, e, i, o, and u.
    ♦ We must clearly write all those 5 elements.
    ♦ We must separate them with commas.
    ♦ We must enclose them within braces.
• So the set will appear as: {a, e, i, o, u}
• If we decide to name the set as V, we can write: V = {a, e, i, o, u}
• Since the order is not important, we can write V = {i, o, a, e, u} also. Different arrangements like this are allowed.

(d) Consider the following set:
• The set of all natural odd numbers.
    ♦ Clearly, the elements are 1, 3, 5, 7, ...
        ✰ These numbers continue indefinitely. We cannot write them all.
    ♦ In such cases, we write the first 4 elements, followed by a comma and 3 dots.
    ♦ We must enclose them within braces.
• So the set will appear as: {1, 3, 5, 7, ...}
• If we decide to name the set as D, we can write: D = {1, 3, 5, 7, ...}
• Here the order is important.

(e) Consider the following set:
• The set of all letters in the word 'SCHOOL'
    ♦ Clearly, the letters are S, C, H, O, O and L.
        ✰ We must write 'O' only once
• So the set will appear as: {S, C, H, O, L}
• If we decide to name the set as E, we can write: E = {S, C, H, O, L}
• Since the order is not important, we can write E = {S, H, C, L, O} also. Different arrangements like this are allowed.

---

Next we will see the set-builder form. It can be explained in 7 steps:
1. We know that, all the elements of a set will possess a common property.
   ♦ All the elements which possess that property should be included into that set.
         ✰ None of such elements should be excluded.
   ♦ Also, objects which do not possess that property should not be included into that set.
2. This gives us an idea to specify a set:
• A set can be specified by writing down the property.
   ♦ A person who reads the property can easily form the set.
3. Let us see an example:
• The property possessed by every element of a set is this:
It is a vowel of English alphabet.
• A person who reads this property will understand that, elements in the set are: a, e, i, o and u.
4. Another example:
• The property possessed by every element of a set is this:
It is positive even integer less than 10.
• A person who reads this property will understand that, elements in the set are: 2, 4, 6, and 8.
5. Mathematicians have specified the form in which the property is to be written.
• By making such a specification, we can ensure that, people all over the world will follow the same form.
◼ It is called the set-builder form.
6. We can familiarize ourselves with the form through some examples:
Example 1:
• The set V of vowels in English alphabet is written in set builder form as:
V = {x : x is a vowel in English alphabet}
• It is read as:
The set of all x such that x is a vowel of the English alphabet.
   ♦ The braces stand for: The set of all.
   ♦ The colon ':' stands for: such that.
• So we can read in the order as shown in fig.1.1 below:

Fig.1.1

 

Example 2:

Fig.1.2

• A person who reads this set-builder form can easily write the corresponding roster form as: A = {4, 5, 6, 7, 8, 9}
7. So now we know how to write the set-builder form.
• Note that, ‘x’ is a variable. We know that, a variable can have different values.
• However, the values taken up by ‘x’ should satisfy the property given after the colon ‘:’.
• Remember that, instead of 'x', we can use, 'y', 'z' etc., also.

---

Let us see the previous examples that we wrote for roster form. We should be able to write each of them in set-builder form also: 

(a) The set of all even positive integers which are less than 7.
• In roster form, we wrote: A = {2, 4, 6}
• In set-builder form, this will be:
A = {x : x is an even positive integer less than 7}

(b) The set of all natural numbers which completely divide 42
• In roster form, we wrote: B = {1, 2, 3, 6, 7, 14, 21, 42}
• In set-builder form, this will be:
A = {x : x is a natural number which completely divide 42}

(c) The set of all vowels in English alphabet.
• In roster form, we wrote: V = {a, e, i, o, u}
• In set-builder form, this will be:
V = {x : x is a vowel in English alphabet}

(d) The set of all natural odd numbers.
• In roster form, we wrote: D = {1, 3, 5, 7, ...}
• In set-builder form, this will be:
V = {x : x is a natural odd number}  

(e) The set of all letters in the word 'SCHOOL'
• In roster form, we wrote: E = {S, C, H, O, L}
• In set-builder form, this will be:
V = {x : x is a letter in the word 'SCHOOL'}

Solved example 1.2
Write the solution set of the equation x² + x - 2 = 0 in roster form.
Solution:
• The given equation can be written as: $\mathbf\small{\rm{x^2+x=-2}}$
⇒ $\mathbf\small{\rm{x^2+x+\left(\frac{1}{2} \right)^2=-2+\left(\frac{1}{2} \right)^2}}$
• We take the half of the coefficient of x. We then add it's square to both sides. Thus we get:
$\mathbf\small{\rm{\left(x+\frac{1}{2} \right)^2=\frac{9}{4}}}$
⇒ $\mathbf\small{\rm{\left(x+\frac{1}{2} \right)=\pm\frac{3}{2}}}$
⇒ x = 1, -2
• So the solution set of the given equation in the roster form is: {1, -2}.

Solved example 1.3
Write the set {x : x is a positive integer and x² < 40}in the roster form.
Solution:
1. The positive integers are: 1, 2, 3, 4,...
• All integers from 1 to 6 will satisfy x² < 40
2. So the values which x can take are: 1, 2, 3, 4, 5 and 6
• Thus the set in roster form is: {1, 2, 3, 4, 5, 6}

Solved example 1.4
Write the set A = {1, 4, 9, 16, 25, . . .} in set builder form.
Solution:
1. It is clear that, the given set contains infinite number of elements. They are the squares of natural numbers 1, 2, 3, 4, . . .
2. So in set-builder form, it will be:
A = {x : x is square of a natural number}
3. Alternatively, we can write: A = {x : x = n², where n ∈ N}

Solved example 1.5
Write the set $\mathbf\small{\rm{\{\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{5}{6},\frac{6}{7}\}}}$ in the set-builder form.
Solution:
1. We see that,
   ♦ each x is a fraction
   ♦ All numerators and denominators are natural numbers
• So they belong to the set N
2. If we denote the numerator as n, the denominator will be (n+1)
• So each x is $\mathbf\small{\rm{\frac{n}{n+1}}}$
3. Thus the set-builder form is: {x : $\mathbf\small{\rm{n=\frac{n}{n+1}}}$ and 1 ≤ n ≤ 6}

---

The link below gives a 4 more solved examples:

Solved examples 1.6 to 1.9 

---

In the next section, we will see the Empty set

Previous

Contents

Next

Copyright©2021 Higher secondary mathematics.blogspot.com