In the previous section, we completed a discussion on determinants. In this section, we will see Continuity and Differentiability.
• We have already learned about limits and derivatives in a previous chapter. The reader is advised to revise those topics thoroughly, before attempting our present chapter.
•
Consider fig.13.5 that we saw in that previous chapter. We can use that figure to learn the basics about continuity. It can be written in 4 steps:
1. In fig.13.5, we wanted the limit at x = 0.
•
We saw that:
♦ The left side limit is 1.
♦ The right side limit is 2.
2. So, the limit at x = 0 does not exist.
3. In general, if at a point c, if the left side limit is not equal to the right side limit, we say that, the function is discontinuous at c. Also, c is a point of discontinuity.
4. Note that, in fig.13.5, at x = 0, we cannot draw the graph without lifting the pen from the plane of the paper. So there indeed, is a "discontinuity".
Let us see another example. It can be written in 5 steps:
1. Consider fig.13.7 that we saw in that previous chapter. We wanted the limit at x = 1.
•
We saw that:
♦ The left side limit is 3.
♦ The right side limit is also 3.
2. So, the limit at x = 1 exists.
•
But value of the function at x= 1, is not 3.
3. So in some cases,
♦ The left side and right side limits may be same at a point c.
♦ But value of the function at c, may be different from that limiting value.
4. The situation mentioned in the above step (3), is also a discontinuity. We say that, the function is discontinuous at c. And, c is a point of discontinuity.
5. Note that, in fig.13.7, at x = 1, we cannot draw the graph without lifting the pen from the plane of the paper. So there indeed, is a "discontinuity".
•
We have seen two examples which were related to two different situations. Those two different situations gave us a basic idea about discontinuity. So now we can write "opposite situations" which will give us a basic idea about continuity. It can be written in 4 steps:
1. A function is said to be continuous at a point c, if two conditions are satisfied:
Condition (i):
♦ The left side limit at c
♦ is equal to
♦ The right side limit at c.
•
Using symbols, we can write this condition as:
$\lim_{x\rightarrow c^{-}} f(x) ~=~ \lim_{x\rightarrow c^{+}} f(x)$
Condition (ii):
♦ Limiting value at c
♦ is equal to
♦ The value of the function at c.
2. It is possible to write the conditions in a simpler way.
•
Consider the first condition that we wrote above. If this condition is satisfied, it means that, limit at c exists. So we can write:
◼ A function is said to be continuous at a point c, if two conditions are satisfied:
Condition (i):
Limit at c exists.
•
Using symbols, we can write this condition as:
$\lim_{x\rightarrow c} f(x)$ exists.
Condition (ii):
♦ Limiting value at c
♦ is equal to
♦ The value of the function at c.
•
Using symbols, we can write this condition as:
$\lim_{x\rightarrow c} f(x)~=~f(c)$.
3. We have seen numerous solved examples where we checked "whether limit at any given point c exists".
•
All we need to do is: Find the limit at c.
•
If the limiting value is in the form 0/0 or "a division by zero", we concluded that, the limit does not exist.
•
Also note that, "finding the limit at c" is essential because, only then we will be able to apply the second condition.
4. When the two conditions are satisfied, we will be able to draw the graph in a single stroke, with out lifting the pen from the plane of the paper.
Let us see some solved examples:
Solved example 21.1
Check the continuity of the function given by f(x) = 2x + 3 at x = 1.
Solution:
1. Applying condition (i):
•
Limiting value of f(x) at x = 1 is:
2(1) + 3 = 5
•
It is clear that, $\lim_{x\rightarrow 1} f(x)$ exists. So first condition is satisfied.
2. Applying condition (ii):
f(1) = 2(1) + 3 = 5
•
We see that: $\lim_{x\rightarrow 1} f(x)~=~f(1)$
•
So second condition is also satisfied.
3. Since both conditions are satisfied, the given function is continuous at x = 1.
Solved example 21.2
Check the continuity of the function given by f(x) = x2 at x = 0.
Solution:
1. Applying condition (i):
•
Limiting value of f(x) at x = 0 is:
(0)2 = 0
•
It is clear that, $\lim_{x\rightarrow 0} f(x)$ exists. So first condition is satisfied.
2. Applying condition (ii):
f(0) = (0)2 = 0
•
We see that: $\lim_{x\rightarrow 0} f(x)~=~f(0)$
•
So second condition is also satisfied.
3. Since both conditions are satisfied, the given function is continuous at x = 0.
Solved example 21.3
Check the continuity of the function given by f(x) = |x| at x = 0.
Solution:
1. Applying condition (i):
This condition can be applied with greater clarity, if we draw the graph. It is shown in fig.21.1 below:
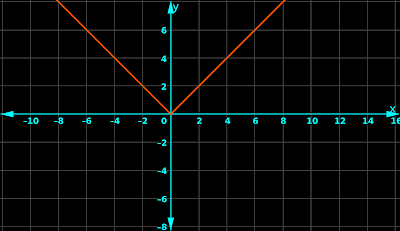 |
| Fig.21.1 |
•
When x approaches zero from the left, f(x) approaches zero. That is: $\lim_{x\rightarrow 0^{-}} f(x) = 0$
•
When x approaches zero from the right, f(x) approaches zero. That is: $\lim_{x\rightarrow 0^{+}} f(x) = 0$
•
Both left side and right side limits are the same. That means, $\lim_{x\rightarrow 0} f(x)$ exists. So first condition is satisfied.
2. Applying condition (ii):
•
From the graph, we have: f(0) = 0
•
We see that: $\lim_{x\rightarrow 0} f(x)~=~f(0)$
•
So second condition is also satisfied.
3. Since both conditions are satisfied, the given function is continuous at x = 0.
Solved example 21.4
Show that the function f given by
$f(x) = \begin{cases} x^3+3, & \text{if}~x\ne0 \\[1.5ex] 1, & \text{if}~x=0 \end{cases}$
is not continuous at x = 0.
Solution:
1. Applying condition (i):
•
Limiting value of f(x) at x = 0 is:
(0)3 + 3 = 3
•
It is clear that, $\lim_{x\rightarrow 0} f(x)$ exists. So first condition is satisfied.
2. Applying condition (ii):
f(0) = 0
•
We see that: $\lim_{x\rightarrow 0} f(x)~\ne~f(0)$
•
So second condition is not satisfied.
3. Since both conditions are not satisfied, the given function is not continuous at x = 0.
In the next section, we will see continuous functions.
Copyright©2024 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment